多项正则化约束的伪标签传播优化脑电信号聚类

代成龙 李光辉 李 栋 申佳华 皮德常

1 （江南大学人工智能与计算机学院 江苏无锡 214122）

2 （南京航空航天大学计算机科学与技术学院 南京 211106）

（chenglongdai@jiangnan.edu.cn）

人类进化进程中形成的最复杂、信息处理最完善的器官就是大脑, 它有效控制着人的情绪、思想和行动, 是人类从外界获取信息、处理信息的重要“工具”. 大脑的认知机制、工作机制以及与相关疾病的关联等都逐渐成为研究学者们所关注的焦点, 也形成了脑科学研究的热潮. 国家中长期科学和技术发展规划纲要（2006—2020 年）针对脑科学进行了研究规划, 其中涉及脑重大疾病的产生机理、脑信息的表达与处理以及人脑与计算机交互等内容. 近年来, 国家则侧重以发展类脑人工智能的计算技术与器件以及研发脑重大疾病的诊断干预方法作为应用导向.2013 年“973”重点资助研究领域的研究内容包括了脑-机一体化以及生机电融合的智能型医疗设备、康复装备的研究. 国家自然基金委重大研究计划“视听觉信息的认知计算”（2008—2017 年）包括了视听觉认知相关的脑-机接口（brain-computer interface, BCI）技术. 2016 年, 脑科学与类脑研究被“十三五”规划纲要确定为重大科技创新项目和工程之一. 目前,“脑科学与类脑科学”作为“科技创新2030 重大项目”已经启动指南意见征求稿. 另外, 近几年的军委装备发展部的支持项目中也涉及基于脑电信号的脑控系统、人机交互接口的研究内容. 可见, 基于脑电信号分析的脑科学技术在未来研究与应用拓展中具有重大意义.

作为一种能有效反映大脑工作状态的媒介, 脑电信号（electroencephalogram，EEG）成为了脑重大疾病辅助诊断、人机交互、康复等领域的重要纽带. 脑电信号是由脑细胞受到刺激产生的生理信号, 即生物电信号. 它不仅能有效反映出当前大脑功能状态,也能反馈人的身体机能状况[1], 因此被广泛应用于神经系统疾病分析[2-5]与康复[6]、脑-机接口[7-8]. 其中, 基于脑-机接口的应用尤为突出, 该应用包含潜在的军事应用[9-10]. 随着脑电信号数据的日益增加, 无标签脑电数据的比重也随之增大, 这给目前普遍的有监督分析方法带来了巨大挑战. 因为有监督的分析方法,如分类, 十分依赖数据的标签信息[5,8,11]. 同时, 人工标记脑电信号既费时又费力, 这也在很大程度上限制了无标签脑电信号这类新型数据在脑-机接口、疾病辅助诊断、康复等领域的应用. 在当前脑电信号的研究环境下, 现有的研究主要存在3 个问题或挑战:

1） 现有的有监督分析方法, 如分类, 需要给定数据标签进行学习训练, 因此无法有效迁移到无标签脑电信号的分析任务中. 而且, 人工标记与日俱增的无标签脑电信号成本高、费时费力.

2） 针对无标签脑电信号的研究相对较少, 可借鉴的分析方法有限, 需要提出新的方案、方法来解决该具有挑战性的任务.

3） 与传统的时间序列数据不同, 脑电信号是一种具有高震荡、高非线性、低信噪比等特点的弱生物信号, 现有的大部分传统时间序列聚类方法可能对无标签脑电信号这类新型数据的处理效果不佳.

为此, 本文提出了一种基于多项正则化约束的伪标签传播优化聚类方法, 旨在充分利用无标签脑电信号自身特征及相关性, 自主学习、优化得到相对最优的脑电信号聚类结果. 具体而言, 本文的主要贡献及工作包括3 个方面:

1） 针对无标签脑电信号的分析问题, 提出了一种基于多项正则化约束的伪标签信息传播优化聚类模型. 该模型充分利用脑电信号之间的相关性与信息传播, 并通过同时学习伪标签传播矩阵、脑电信号相似度邻接矩阵、标签分类器的方式实现无标签脑电信号聚类.

2） 为了解决由脑电信号聚类转化的多目标优化问题, 提出了一种基于梯度下降策略的多目标优化算法EEGapc（electroencephalogram clustering with pseudo label propagation）. 该算法能在一个很小的学习率条件下很快收敛到局部最优, 不仅确保了多目标函数的可解性, 也有利于脑电信号的快速聚类.

3） 通过在14 个真实脑电信号数据集、4 个评价指标上的实验分析, 展示了本文提出的EEGapc 算法的性能优越性. 与现有的多种聚类算法相比, 本文提出的EEGapc 算法能得到更优的聚类结果.

1 相关工作

随着脑电信号规模在脑-机接口应用、疾病诊断、康复等领域的不断增大，无标签或误标记脑电信号的数量也随之增加，特别是针对患有脑部疾病的被试所采集的脑电信号, 其标签缺失、误标尤为突出[12]. 同时，人工标记脑电信号是一件费时费力的事情，在一定程度上制约了脑电信号的应用. 因此，针对无标签脑电信号这类新型数据进行研究，既能拓展其应用范围，也能为其提供鲁棒性更高、性能更好的分析策略与方法.

作为一种有效的无监督分析方法, 聚类可以用来处理无标签脑电信号. 目前专门针对脑电信号的聚类研究相对较少, 主要是基于相似度衡量和中心搜寻相结合的脑电信号聚类方法, 如MTEEGC （multitrialelectroencephalogram clustering）[13], FCM （fuzzy Cmeans）[14]，以及基于图的脑电信号聚类方法, 如mwc-EEGc （maximum weight clique electroencephalogram clustering）[15]. 具体而言，MTEEGC 采用一种互相关相似度衡量方法评估脑电信号之间的相关性，并利用优化目标函数搜寻聚类中心，最后根据脑电信号与聚类中心的相似度实现脑电信号聚类；FCM 脑电信号聚类方法与k-means 相似, 通过判断脑电信号与聚类中心的相对距离实现脑电信号的聚类. 这类脑电信号聚类方法的性能在很大程度上受聚类中心初始化与中心更新策略的影响. mwcEEGc 同样先利用相似度衡量方法评估脑电信号之间的相关性权重, 并将脑电信号及其相关性权重映射为一个无向加权图,最后结合相似度阈值搜寻图中最大加权团的方式实现脑电信号聚类. 该脑电信号聚类方法虽然具有较高的性能, 但多次的最大加权团搜寻过程会消耗大量的时间, 对于实时性要求较高的应用而言, 如脑-机接口等, mwcEEGc 的应用会受到一定限制.

由于面向无监督分析的脑电信号研究方法有限,在一定程度上影响了日益增长的无标签脑电信号的分析和应用拓展. 幸运的是, 作为一种具有时间序列特性的生物电信号, 丰富的时间序列聚类方法可以为脑电信号聚类提供方法指导. 目前, 涉及到脑电信号聚类的研究方法也通常是基于时间序列的聚类策略[13-14], 如MTEEGC, FCM. 一般而言，基于时间序列的聚类方法主要通过自身的学习、优化策略, 例如数据之间的相关性、数据特征之间的相关性等进行自动划分, 最终实现数据的聚类[12,15]. 目前为止, 基于时间序列的聚类方法可以大致分为6 类:

1） 经典的k-means 型聚类算法[16]. 这类算法继承了经典k-means 的聚类策略, 即根据数据与初始化聚类中心之间的距离, 迭代更新聚类中心并根据预先设定好的聚类个数将数据划分到与其最近的聚簇中,达到聚类的目的, 如k-means++[17], k-variates++[18], KMM（K-multiple-means）[19]等. 不难看出, 这类k-means 型聚类方法的性能依赖于一个合适的初始化策略或一个中心（重心）搜寻更新方法. 换言之, 这类聚类方法的最终效果对聚类中心（重心）的初始化要求较高,虽然效率高, 但聚类精度通常相对较差.

2） 基于相似度的聚类. 该类方法主要利用相似度（或距离）衡量方法评估数据之间的相关性, 并结合设定的相似度阈值将满足条件的数据划分到同一聚簇中, 如DBA （dynamic time warping barycenter averaging）[20], K-SC （K-spectral centroid）[21]等. 这类聚类算法主要依赖于相似度（或距离）衡量方法, 并在聚类过程中也涉及到聚类中心的搜寻, 因此这类算法在计算数据相似度且根据相似度衡量方法不断更新聚类中心时会消耗大量的时间, 所以它们的时间复杂度相对较高.

3） 基于密度的聚类. 这类方法主要利用预先设定的密度评估参数衡量数据之间构成的稠密区域是否满足最低密度阈值, 从而实现数据的聚类划分. 基于密度的方法有DBSCAN （density-based spatial clustering of applications with noise）[22], OPTICS （ordering points to identify the clustering structure）[23], SNN （shared nearest neighbor）[24], DP （density peak clustering）[25-27]等. 这类方法的效率较高, 但聚类性能也受到密度评估参数的影响. 而且, 基于密度的方法通常情况下对“点”型数据聚类效果相对较好, 而对于时间序列数据而言相对较差.

4） 基于特征选择的聚类. 这类方法主要从数据降维的角度, 通过特征识别与选择方法将原始数据映射到低维的特征空间, 然后利用数据与特征之间的相关性进行聚类操作, 如NDFS （nonnegative discriminative feature selection）[28], RUFS （robust unsupervised feature selection）[29], RSFS （robust spectral learning framework for unsupervised feature selection）[30], CGSSL（clustering-guided sparse structural learning）[31]等. 虽然这类方法将降低原始数据的维度, 但其聚类性能同样也受到特征识别与选择方法以及特征个数设定的影响. 而对于特征复杂的脑电信号而言, 特征提取的时间消耗也比较大.

5） 基于数据形态的聚类. 这类方法与基于特征选择的聚类方法策略相似, 通过学习将原始数据用较短的数据段, 即数据形态, 降低原始数据的维度,然后利用学习到的多个数据形态与原始数据之间的相互关系进行聚类操作, 如u-shapelet （clustering using unsupervised shapelets）[32], USSL （unsupervised salient subsequence learning）[33], kShape （k-shape clustering）[34]等. 同理, 这类方法的聚类性能同样受到数据形态学习方法的影响. 而且, 想要学习到差异性较高、代表性较强的形态数据段也需要一个良好的学习目标函数和大量的学习时间.

6） 谱聚类. 这类方法是基于图的聚类策略, 通过将数据映射为图中节点, 数据之间的相关性映射为图边上的权重, 然后进行图分割实现聚类, 例如BSGP（bipartite spectral graph partition）[35], USPEC （ultrascalable spectral clustering）[36]等. 谱聚类需要数据构成的相似度矩阵, 然后根据拉普拉斯矩阵进行相似度变换, 最后进行图分割. 这类方法对数据结构无需过多的假设要求, 也不需要对数据的概率分布做假设.同时, 通过构造稀疏相似度图, 可以降低聚类的时间消耗. 但是, 谱聚类方法对图相似度比较敏感.

本文针对无标签脑电信号进行聚类分析, 提出了一种基于图的伪标签传播优化聚类方法. 在多项正则化的约束下, 建立多目标优化模型, 即将伪标签传播学习与脑电信号相似度邻接矩阵正则化约束和标签分类器正则化约束相结合, 从而学习到与真实标签接近的伪标签, 实现无标签脑电信号的聚类任务.

2 准备工作

聚类最本质的目的是将相似度高的数据划分到同一聚簇中, 并使得聚簇之间的差异最大化. 本文采用的基于图的聚类方式的主要目的也是将相似度较高的脑电信号通过图中的边权重将脑电信号划分到对应的子图中, 这个过程类似于谱聚类. 为了让文章更好地被理解, 在详细介绍本文方法之前, 先对方法涉及到的相关知识, 如拉普拉斯矩阵等进行简要介绍.

假设G=（V,E）为脑电信号构成的无向加权图,其中,V={e1,e2,···,en}为n条脑电信号构成的图节点,E为图中节点之间的边. 对于边（ei,ej）上的权重sij，sij为邻接矩阵S的元素, 本文采用皮尔逊相关系数的变形方式来衡量, 即给定2 条长度为m的脑电信号ex与ey, 它们之间的皮尔逊相关性rxy[37]定义为

最终由sxy构成脑电信号相似度邻接矩阵S,S=(sxy),sxy∈[0,1].

基于脑电信号相似度邻接矩阵S, 脑电信号构成的图结构中拉普拉斯矩阵LS定义为

其中rank(LS)=n-c,c为LS特征值为0 的个数, 也表示为图G中可划分的子图个数[38-39]; 同时,D= (di) =(dii) 为对角矩阵上的元素, 定义为

对于标准的基于图的聚类, 其目的是将相似度较高的数据划分到同一聚簇中, 因此一个好的相似度衡量策略有利于得到更好的聚类结果. 对于基于图的聚类而言, 其相似度矩阵可以作为数据间的传播信息, 有利于将相关性较高的数据划分到同一聚簇中, 提高数据的聚类效果. 换言之, 无标签数据的类标也可以通过数据间的信息传播, 实现标记的动态学习与优化, 从而实现无标签数据的标签化,即聚类[40].为了更好地基于相似度邻接矩阵对无标签脑电信号的标签进行传播学习, 可以将脑电信号相似度邻接矩阵S重定义为一个传播矩阵[41]:

本文中采用的伪标签传播学习则可以定义为

其中0 ＜α ＜1为权重系数，L∈Rc×n为伪标签指示矩阵.L=(Li j)具体定义为

伪标签指示矩阵L表示: 对于一个c聚类问题,当脑电信号ei被划分到第j类聚簇中, 即li=j, 则有Lij=1, 否则Lij=0. 当然, 该伪标签会根据优化策略不断地更新.

为了能更好地让标签信息（即脑电信号的相似度邻接矩阵所包含的信息）在整个图结构中平稳传播, 实现未标记节点的标签化, 本文将标准的标签传播模型引入正则化约束, 最后形成正则化标签传播模型[41]：

其中c为聚类个数， γ为正则化系数且用来平衡模型中的约束权重.

3 本文提出的聚类算法EEGapc

为了解决无标签脑电信号聚类问题, 提出了一种多项正则化约束的伪标签传播学习脑电信号聚类模型. 该方法主要结合了邻接矩阵传播优化、伪标签传播学习及伪标签分类器优化等模块, 充分利用脑电信号之间的相关性进行聚类.

3.1 邻接矩阵传播优化

根据文献[38]提出的理论: 与邻接矩阵相关的拉普拉斯矩阵中特征值为0 的数量与图中相连子图的个数相同. 可用该理论对脑电信号构建的图进行划分, 实现脑电信号聚类. 对于原始脑电信号相似度构成的初始邻接矩阵M∈Rn×n, 文献[38]中提出的聚类方法的目的是学习到一个与M相当接近的伪邻接矩S∈Rn×n, 并使得与之相关的拉普拉斯矩阵满足以下约束条件rank(LS)=n-c. 为了得到与真实邻接矩阵M最接近的伪邻接矩阵S, 定义其优化目标函数为

其中1n=(1,1,···,1)T.

3.2 伪标签传播学习

结合标签传播学习函数, 见式（8）, 正则化约束能更好地利用脑电信号之间的相互关系, 即脑电信号之间的相似度信息, 为未标记脑电信号进行标签学习. 不难看出, 标准的标签传播学习函数可收敛到最优解, 如定理1 所述.

定理1.当0 ＜α ＜1时, 标签传播函数（式（8））可收敛到最优解：P*=(1-α)L(I-αQ)-1.

证明. 为了不失一般性, 首先定义P0=L, 式（6）的迭代更新过程则可等价为

结合在邻接矩阵优化中定义的约束条件:S1n=1n,所以Q=D-1/2SD-1/2=S，且有0 ＜sij＜1. 同时, 因为0 ＜α ＜1, 所以可知以及αS)-1, 其中I表示单位矩阵.

综上所述, 可以得到

定理1 中的结论将用于后文求解多目标函数. 在本文提出的方法中, 对于脑电信号伪标签传播学习,则可以通过正则化约束来获得最优的伪标签, 具体表示为

其中||·||F为Frobenius 范数, γ为正则化参数. 结合脑电信号相似度邻接矩阵的约束条件S1n=1n, 可得D=I. 因此, 式（12）最终变换为

3.3 伪标签分类器优化

本文方法旨在将未标记的脑电信号划分到正确的聚簇中, 除了利用伪标签传播学习与脑电信号相似度邻接矩阵优化策略外, 还采用了正则化标签分类器优化来约束脑电信号的伪标签学习，即通过最小化伪标签正则化误差来学习最优分类器, 具体表示为

该正则化约束函数不仅可以学习满足约束条件的脑电信号标签分类器W, 同时还能进一步约束优化脑电信号的相似度邻接矩阵S, 有利于得到满足约束条件的解, 从而提升脑电信号的聚类性能.

3.4 聚类模型建立

充分利用脑电信号之间的信息传播, 在图的基础上, 基于伪标签传播学习建立了多项正则化约束下的多目标优化模型, 以确保脑电信号之间的信息传播正确性与聚类准确性. 建立的多目标优化模型主要包含了伪标签传播学习、脑电信号相似度邻接矩阵优化和伪标签分类器优化等模块. 具体的模型公式化为

其中γ1,γ2,γ3,γ4为正则化参数, 用于平衡约束项的权重. 式（15）中的前2 项为伪标签传播学习模块, 用于在脑电信号相似度邻接矩阵的优化约束下学习得到接近真实结果的伪标签；第3, 4 项为标签分类器的优化学习模块, 同样也是为了在脑电信号相似度邻接矩阵约束下学习得到最优的伪标签; 最后1 项是邻接矩阵优化模块, 用于学习最接近原始脑电信号相似度邻接矩阵的伪邻接矩阵, 同时也为优化伪标签传播矩阵与标签分类器提供更好的传播信息.

3.5 脑电信号聚类算法 EEGapc 介绍

由于多目标优化函数, 即式（15）, 严格意义上是非凸的, 并不能得到全局最优解, 因此利用梯度下降策略求解目标函数的局部最优解. 通过固定其他变量的方式得到各个变量的局部最优解.

3.5.1 更新伪标签传播矩阵P

伪标签传播矩阵P的更新可以通过固定伪标签L、脑电信号相似度邻接矩阵S和标签分类器W来实现. 此时, 目标函数（式（15））关于P的弱化函数变换为

式（16）的偏导为

式（18）与式（11）一致.

3.5.2 更新伪标签L

为了更新伪标签L, 同样固定其他变量即可. 因此, 目标函数（式（15））关于L则可以弱化为

式（19）关于L的偏导为

3.5.3 更新标签分类器W

同理, 为了更新标签分类器W, 固定其他变量.目标函数（式（15））关于W的弱化函数变为

式（23）关于W的偏导可表示为

3.5.4 更新邻接矩阵S

固定伪标签L、伪标签传播矩阵P和标签分类器W, 目标函数（式（15））关于脑电信号相似度邻接矩阵S可以弱化为

由于式（26）不是一个严格意义上的凸函数, 为了得到其最优解, 采用了梯度下降方法对其进行求解. 即, 设定一个学习率 η, 让S梯度下降, 逼近最优解:St+1=St-η∇St. 同理, 式（26）的偏导可表示为

根据目标函数（式（15））中的约束条件S1n=1n,可以得到邻接矩阵的对角矩阵D=diag(S1n)=I, 所以可知LS=D-S=I-S, 最后可以得到

同时，根据式（18），得到

最后, 根据式（27）～（29）, 脑电信号相似度邻接矩阵可以更新为

3.5.5 脑电信号聚类算法 EEGapc

根据多目标优化函数中各个变量的更新求解过程，提出的脑电信号聚类算法EEGapc 的具体描述见算法1.

算法1.脑电信号聚类算法EEGapc.

输入: 脑电信号E∈Rn×m，正则化参数γ1,γ2,γ3,γ4，学习率 η，最大迭代次数imax；

输出:L*,P*,W*,S*.

① 计算脑电信号相似度初始邻接矩阵M；

② 初始化L0,P0,W0,S0；

③ while 目标函数未收敛do

④ 计算脑电信号相似度初始邻接矩阵M；

⑤ 更新伪邻接矩阵St+1：

⑥ fori=1∶imaxdo

⑧Si+1=Si-η∇Si；

⑨ end for

⑩St+1=Simax+1；

⑪ 更新伪标签分类器Wt+1：

⑬ 更新伪标签传播矩阵Pt+1：

⑭Pt+1=γ1Lt(LSt+1+γ1I)-1；

⑮ 更新伪标签Lt+1:

⑰t=t+1；

⑱ end while

⑲ returnL*=Lt+1,P*=Pt+1,W*=Wt+1,S*=St+1.

3.6 收敛性分析

由于邻接矩阵更新函数并不是一个严格意义上的凸函数, 故不能有效得到其全局最优解. 因此, 采用了梯度下降策略来获得其局部最优解. EEGapc 可以在设定好的学习率条件下收敛到局部最优解.

引理1. 对于函数f(x) ∶Rn→R, 其梯度下降更新策略为xt+1=xt-η∇f(x). 在足够小的学习率 η下, 该函数可收敛到最优解x*.

证明. 根据文献[42], 对于函数f, 其梯度下降∇f在尺度系数µ＞0条件下满足Lipschitz 连续, 即

对f（y）进行泰勒二项展开可得

对式（32）进行变换可得

结合梯度下降更新策略xt+1=xt-η∇f(x), 可得

结合式（33）, 可以得到

又因为f(xt)-f(x*)≠0, 以及∇f(x*)=0, 所以不等式（35）等价为

综上所述,

结合引理1, EEGapc 在足够小的学习率η条件下可以收敛到局部最优解, 如定理2 所述.

证明. 针对式（15）（16）（19）（23）（26）中的目标函数及关于各参数弱化后的表达形式, 结合文献[33],我们先构建以下形式的表达式：

其中wi,ai,bi∈R.

根据引理1, 容易得出式（38）可以收敛到最优解,并且有

同时, 可以得到

同理可得,

相应地,

综上所述, 结合引理1 中的不等式（37）, 当学习率为且的下界时, 构建的式（31）利用梯度下降算法可以收敛到最优解x*. 显然, 本文提出的聚类模型目标函数（式（15））及各变量弱化后的表达式均可以转换为式（38）的形式. 因此, 基于梯度下降策略的算法EEGapc 在给定的合适学习率条件下可以收敛到局部最优解.证毕.

3.7 模型初始化

由于本文提出的脑电信号聚类模型所变换的多目标优化函数并不是一个严格意义上的凸函数, 不能得到全局最优解. 因此, 本文采用了梯度下降策略来求解其局部最优解. 对于EEGapc 而言, 合适的初始化有利于得到较好的聚类性能, 因此，对EEGapc 初始化也进行了相应介绍.

3.7.1 伪邻接矩阵S0初始化

EEGapc 其中一个优化目标是学习到相对最优的脑电信号相似度伪邻接矩阵S∈Rn×n, 使其接近于脑电信号的原始相似度矩阵M∈Rn×n. 结合多目标优化函数中的约束条件S1n=1n, 1n=(1,1,···,1)T, 故本文将S0初始化为S0=M, 并进行归一化使其满足S1n=M1n=1n.

3.7.2 伪标签L0初始化

本文通过k-means 算法先粗略为无标签脑电信号分配标签, 即利用k-means 将n条脑电信号划分到c个聚簇中, 并对其标签赋予伪标签L0∈Rc×n； 然后再根据多目标优化函数的更新策略对其进行优化,使其满足目标函数的最小化约束要求.

3.7.3 伪标签传播矩阵P0初始化

结合初始化的脑电信号相似度邻接矩阵S0和初始化伪标签L0, 标签传播矩阵的初始化P0∈Rc×n可根据式（11） 实现, 即

根据文献[40], 通常情况下α=0.99.

3.7.4 伪标签分类器W0初始化

为了得到相对最优的脑电信号聚类结果, EEGapc利用标签分类器的优化对伪标签传播学习进行了约束, 该约束的目的是为了学习与最初的脑电信号相似度邻接矩阵接近的标签分类器, 提升脑电信号之间的信息传播准确性, 并最终将n条脑电信号更准确地划分到c个聚类中. 因此, 本文将标签分类器W0∈Rn×c初始化为

利用3.7.1～3.7.4 节中所述的4 个模块（矩阵变量）的初始化，EEGapc 可以在预先设定好的学习率 η条件下进行迭代优化, 直至目标函数收敛到局部最优,从而最终得到脑电信号的聚类结果.

3.8 时间复杂度分析

如算法1 所示, 采用了梯度下降的策略求解多目标优化函数的局部最优解, 该过程需要通过多次迭代更新、优化, 也是算法1 最主要的时间消耗. 从理论角度分析了算法EEGapc 的时间复杂度.

在算法1 中, 首先计算原始脑电信号相似度矩阵M, 如算法第①行, 其时间复杂度为O（n2），其中n表示脑电信号的条数；如算法第②行所示, 初始化L0,P0,W0,S0, 分别需要的时间为O（n2）,O（n3+cn2+n2）,O（n3+n2+cn）,O（n2）. 当各个变量初始化后, 算法EEGapc进行迭代优化、更新, 直到目标函数收敛到局部最优. 该过程需要多次迭代, 如算法第③～⑱行. 对于每一次迭代, 如算法第⑥～⑩行, 利用梯度下降更新S的时间复杂度为O（imax（2n3+6cn2+3n2+3cn））；如算法第⑫行所示, 更新W的时间复杂度为O（2n3+2cn2+cn）；更新P（如算法第⑭行）的时间复杂度为O（n3+cn2+n2）；更新L的时间复杂度为O（2n3+2cn2+2n2+cn）, 如算法第⑯行所示. 假设目标函数经过iter次迭代优化后收敛到局部最优, 则整个过程的时间复杂度为O（iter×（5n3+5cn2+3n2+2cn+imax（2n3+6cn2+3n2+3cn）））. 综上，包含初始化与迭代优化过程的整个算法时间复杂度为O（2n3+2cn2+4n2+cn+iter（5n3+5cn2+3n2+2cn+imax（2n3+6cn2+3n2+3cn）））. 实际上, 采用的脑电信号数据集类别个数c远小于数据条数n, 所以算法EEGapc 的实际时间复杂度可以表示为O（n3+iter（n3+imaxn3））. 不难看出,一旦初始化得到脑电信号的原始相似度, EEGapc 在聚类过程中的时间消耗仅与脑电信号的条数有关,而与其长度无关. 而且通常情况下, 脑电信号的条数也远远小于其长度, 这也使得EEGapc 在聚类过程中具有较高的效率.

4 实验与讨论

4.1 数据集

采用了目前应用广泛的公共脑电信号数据集对EEGapc 进行性能分析，数据主要来源于国际BCI 竞赛①网站分别为https://www.bbci.de/competition/ii/, https://www.bbci.de/competition/iv/, 主要包括： 1）慢皮质脑电信号（slow cortical potential, SCP），其中一个数据集II_Ia 采集于1 个健康被试，另一个数据集II_Ib 来源于1 个渐冻症患者.2） 四分类运动想象脑电信号，该数据集采集了9 个健康被试的左手、右手、双脚和舌头的运动想象脑电信号，分别对应数据集IV_2a_s1，IV_2a_s2，IV_2a_s3，IV_2a_s4， IV_2a_s5， IV_2a_s6， IV_2a_s7， IV_2a_s8，IV_2a_s9. 3） 简单二分类运动想象脑电信号，采集了3 个健康被试的左手和右手运动想象脑电信号，分别对应数据集IV_2b_s1，IV_2b_s2，IV_2b_s3. 14 个脑电信号数据集的具体描述如表1 所示. 表1 中，1 条脑电信号是由所有有效通道在同一时间段采集到的同一脑任务刺激所产生的脑电信号依次拼接而成的，该操作便于衡量脑电信号之间的相关性，即相似度.同时，该处理方式也比较适用于其他基于时间序列的聚类算法进行脑电信号的聚类，便于与EEGapc 进行聚类性能比较. 另外，采用的脑电信号已经人工剔除了无用采集通道及伪迹数据, 如肌电信号、眼电信号等.

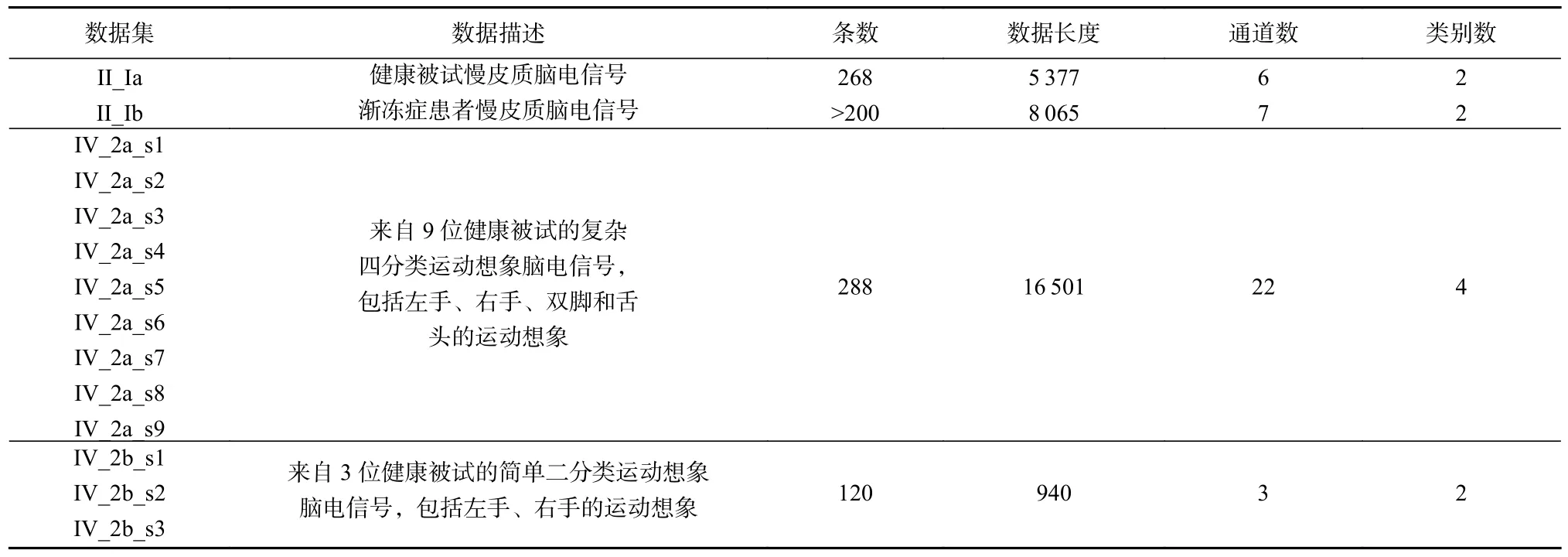
Table 1 EEG Data Sets表1 脑电信号数据集

4.2 评价指标

采用4 种聚类评价指标:NMI（normalized mutual information）[43],ARI（adjusted rand index）[44],F-score[45],kappa[46]对提出的脑电信号聚类算法性能进行评价.

1）NMI

NMI衡量聚类结果与真实结果之间的相似程度,即可以有效衡量聚类算法的聚类准确性. 定义为

其中|Ci|与|Cj|分别表示聚类Ci与Cj中的元素个数即脑电信号条数，v表示脑电信号的类别数，N表示脑电信号的总条数.

2）ARI

ARI是标准rand index （RI）的一种改进,RI=可以衡量2 个随机划分的匹配程度, 即可以在类标不明确的情况下衡量聚类结果与真实结果的匹配情况.ARI的具体定义为

其中nij表示类别 µi与类别vj交集中的元素个数，ai表示类别 µi包含的元素个数，bi表示类别vi包含的元素个数，n为所有数据元素的总个数.

3）F-score

F-score采用了一种非平等加权的方式来衡量聚类算法的性能, 即对召回率增加了尺度权重β ≥0. 其具体定义为

4）kappa

kappa用以估计出现一致性的概率, 即可用于衡量聚类决策（结果）的一致性, 其具体定义为

其中

4.3 对比算法

为了评估EEGapc 的脑电信号聚类性能, 将其与其他时间序列聚类算法进行比较. 主要对比了8 种聚类算法, 包括经典的k-means 型聚类算法KMM[19]、基于距离（相似度）的聚类算法K-SC[21]、基于密度的聚类算法DP[26]、基于特征选择的聚类算法RUFS[29]、基于形态的聚类算法kShape[34]、谱聚类USPEC[36]、基于邻接矩阵传播优化的聚类算法AP[40]以及基于最大加权团的脑电信号聚类算法mwcEEGc[15].

1）KMM. 该算法是一种k-means 型聚类算法, 其首先设定多个聚类子中心, 然后通过优化策略更新子聚类中心及子聚类结果, 经过多次优化、更新及融合, 将数据划分到k个聚类中.

2）K-SC. 该算法首先采用一种尺度可伸缩的相似度衡量方法迭代搜寻聚类中心, 然后再结合数据与聚类中心的相似度进行数据划分与聚类中心更新,直到聚类中心不再变化, 且所有数据被划分到相应的聚类中.

3）DP. 该算法根据数据之间构成的团体密度进行聚类, 即根据各数据与其周围数据的密度高低确定聚类中心, 然后再根据密度阈值将数据划分到对应的高密度数据团体中, 即聚类中.

4）RUFS. 该算法利用l2,1范式最小化与局部正则化后的正交矩阵实现数据的特征选择与降维, 然后将具有相似特征的数据划分到相应的聚类中.

5）kShape. 该算法利用标准化互相关衡量方法评估数据间的相关性, 并利用该方法得到数据差异性较大的数据形态, 最终结合学习到的形态特征将相似的数据划分到同一聚类.

6）USPEC. 该算法采用混合特征搜寻策略和kNN相结合构建稀疏邻接矩阵, 并利用转切（transfer cut）策略实现数据的聚类任务.

7）AP. 该算法于2014 年发表在Science 上, 其主要利用数据相似度邻接矩阵作为数据之间的传播信息, 该传播过程为无标签数据的标签化提供有效信息, 最终实现数据的聚类.

8）mwcEEGc. 该算法利用改进的Fréchet 距离衡量脑电信号之间的相似度, 并将其映射为脑电信号无向加权图的边权重, 然后结合相似度阈值, 以搜寻图中最大加权团的方式实现脑电信号聚类.

以上8 种对比方法的参数设定与相应文献的原文设定一致；聚类数量根据脑电信号数据原本的类别数确定；提出的EEGapc 算法的参数γ1,γ2,γ3,γ4采用网格搜寻的方式自动寻优, 即它们的取值范围设定为{10-2,10-1,1,101,102}；学习率 η设定为0.01；算法的最大迭代次数为50 次. 本文将参数自动寻优后取得的最佳结果作为EEGapc 的最终聚类结果. 另外, EEGapc由Matlab R2021b 实现, 且在MacOS 12.1 （M1 Pro、8核处理器、16 GB 内存）上运行. 对比算法均运行10 次, 并取最优结果作为最终聚类结果.

4.4 实验及分析

4.4.1 聚类结果比较

为了评价EEGapc 的脑电信号聚类性能, 比较了EEGapc 与上述8 种聚类算法在NMI,ARI,F-score,kappa这4 个指标下的聚类结果, 分别如表2～5 所示.结果表明, 与8 种不同的聚类算法相比，EEGapc 脑电信号聚类算法在14 个真实脑电信号数据集上的聚类性能最好. 表2～5 中的NMI均值、ARI均值、F-score均值和kappa均值表明了EEGapc 在不同类型的无标签脑电信号上的聚类性能稳定性与优越性. 而且，EEGapc 脑电信号聚类算法与其他8 种聚类算法中性能最好的mwcEEGc 相比, 分别在NMI均值、ARI均值、F-score均值和kappa均值上分别提升了86.88%,58.01%, 6.29%, 61.17%. 另外, 表2～5 中的显著性分析结果也表明，EEGapc 脑电信号聚类算法性能与KMM,K-SC, DP, RUFS, kShape, USPEC, AP 的相比具有显著性优势. 潜在原因主要是因为EEGapc 聚类算法利用多项正则化对伪标签传播矩阵优化进行了约束, 并且充分利用了以脑电信号相似度邻接矩阵为载体的传播信息, 为得到相对最优的脑电信号标签提供了更符合实际情况的优化方向.

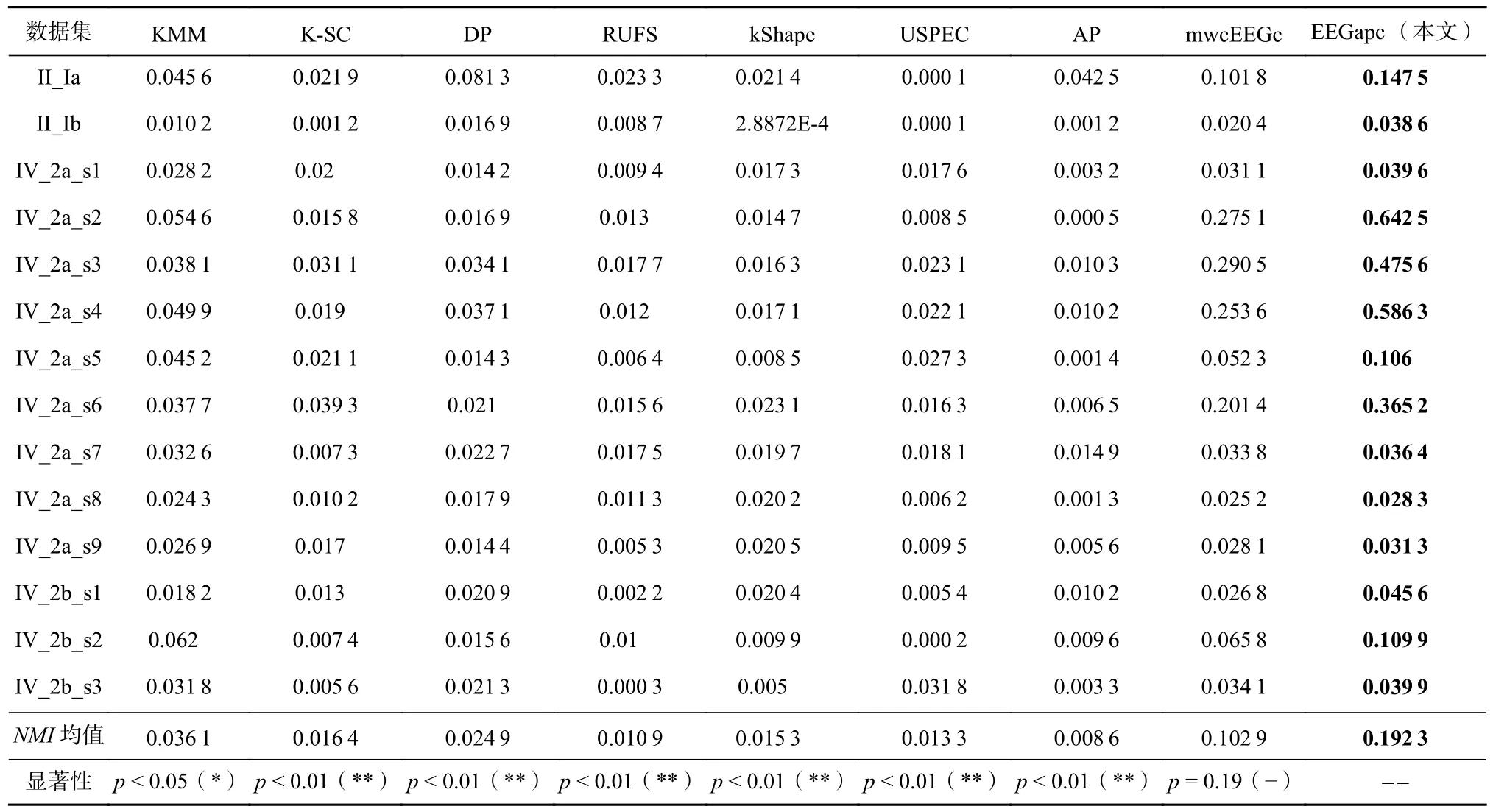
Table 2 Performance Evaluation with NMI for Clustering Algorithms表2 聚类算法的 NMI 性能指标

Table 3 Performance Evaluation with ARI for Clustering Algorithms表3 聚类算法的 ARI 性能指标

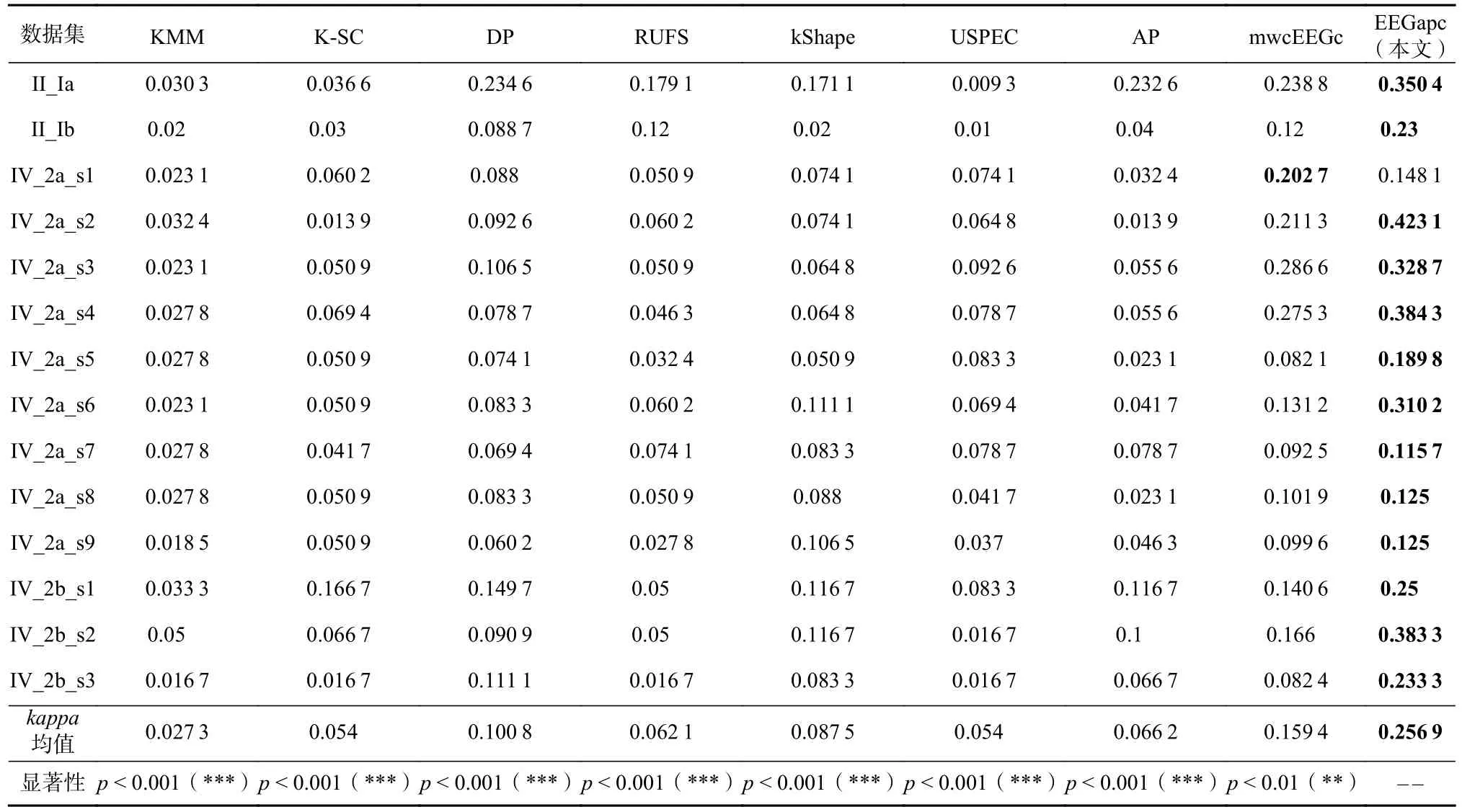
Table 5 Performance Evaluation with kappa for Clustering Algorithms表5 聚类算法的 kappa 性能指标

另外, 为了更直观地展示各聚类算法在14 个脑电信号数据集上的整体聚类性能（也可以理解为聚类算法的通用性）, 对表2～5 中聚类算法的NMI,ARI,F-score,kappa评价指标结果进行了排序：评价指标越高, 排名数值越小（即排名越靠前）；然后, 计算出各聚类算法的平均评价指标排名, 平均排名越低, 表明聚类性能越好, 具体结果如图1 所示. 图1 中的平均排名结果同样表明EEGapc 算法的整体聚类性能最佳, 且具有在不同类型脑电信号数据集上保持性能稳定的能力, 这也从侧面反映出EEGapc 聚类算法可以应用到不同规模、类型的脑电信号数据集上.

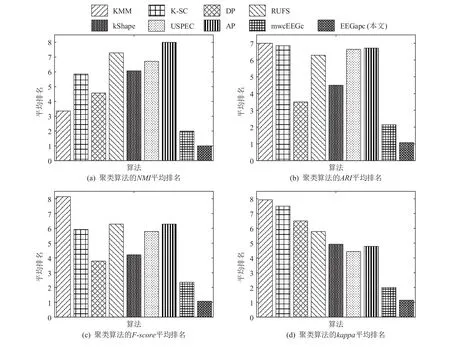
Fig.1 Performance average rank of clustering algorithms图1 聚类算法的性能平均排名

4.4.2 聚类效率比较

本节主要比较EEGapc 与其他聚类算法在14 个脑电信号数据集上的聚类效率. 需要说明的是, 本文仅将固定正则化参数下的运行时间作为EEGapc 的聚类时间消耗, 并没有将自动参数寻优的总体时间作为EEGapc 的最终运行时间. 与不同聚类算法的比较结果如图2 所示. 该结果展示了EEGapc 聚类算法在所有的脑电信号数据集上都具有较好的运行效率,聚类的时间消耗比大部分对比算法小. 正如3.8 节的阐述, 在聚类过程中, EEGapc 的聚类时间消耗与脑电信号的条数有关, 与脑电信号的长度无关. 通常情况下, 脑电信号的条数远小于长度. 一旦脑电信号的相似度初始化, EEGapc 便能快速地进行迭代学习和收敛, 并最终实现脑电信号聚类. 与EEGapc 相似, USPEC,DP, KMM, AP 的聚类时间消耗也主要与脑电信号的条数有关, 而不是其长度, 因此它们的聚类时间消耗也相对较小. USPEC, DP, KMM 的聚类时间之所以小于EEGapc, 是因为它们在聚类过程中采用了相对简单的聚类中心确定策略. 相反, RUFS, kShape, K-SC, mwcEEGc等聚类算法的时间消耗不仅与脑电信号的条数有关,更与脑电信号的长度有关, 因为它们都需要多次处理整条脑电信号, 从较长的脑电信号中识别、提取和搜寻特征、形态和聚类中心或多次迭代搜寻最大加权图, 直到所有脑电信号被划分到相应的聚类为止,这大大增加了它们的时间成本. 特别地, kShape, K-SC,mwcEEGc 在聚类过程中用来计算脑电信号相似度的方法复杂度较高, 这也是导致它们聚类效率较低的原因之一.

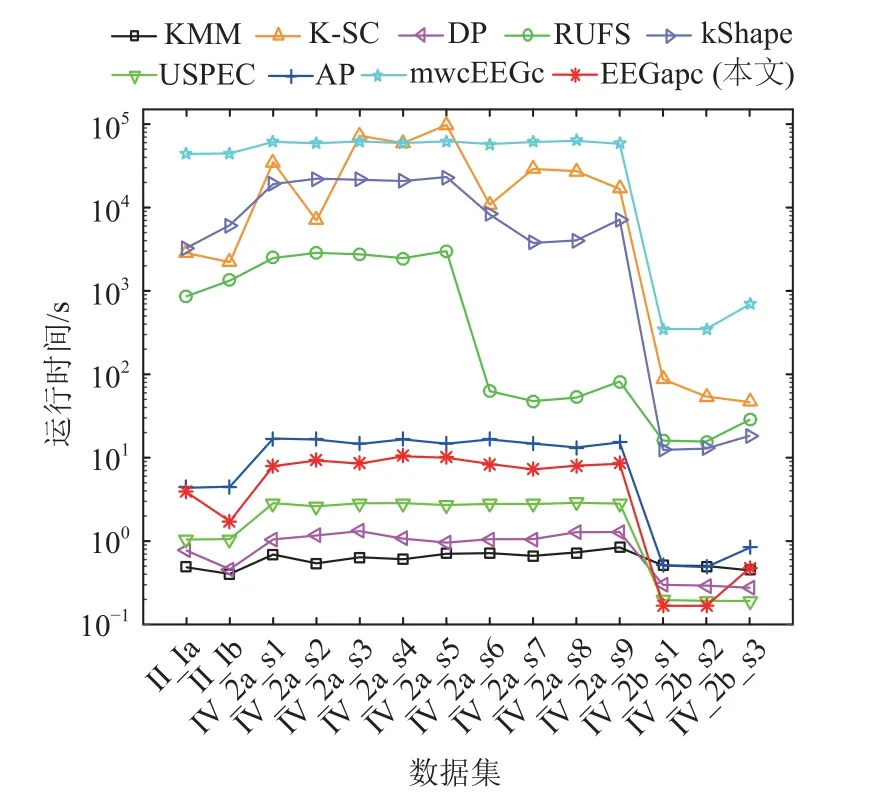
Fig.2 Runtime comparison of clustering algorithms图2 聚类算法的运行时间比较

不难看出: 根据14 个脑电信号数据集的规模,EEGapc 算法的聚类时间消耗并没有随着脑电信号数据集的规模增大而明显增加, 这也表明EEGapc 对于规模更大的脑电信号在理论上也可以在较短时间内完成数据标签化. 同时, EEGapc 聚类算法的高效率也在一定程度上归功于它的快速收敛特性, 如图3所示.

4.4.3 收敛性分析

图3 展示了EEGapc 聚类算法在6 种不同规模、类型的脑电信号数据集II_Ia，II_Ib，IV_2a_s1，IV_2a_s5，IV_2a_s9，IV_2b_s1 上的收敛情况，其他数据集的收敛情况与图3 相似，故未在文中全部展示. 从图3可以看出，EEGapc 在不同类型脑电信号数据集上都能在较少的迭代后收敛，这也表明EEGapc 能很快速地得到多目标优化函数的局部最优解和脑电信号聚类结果. 同样，图3 中的结果也表明即使在规模更大的脑电信号数据集上，EEGapc 也能在较短的时间内收敛并得到聚类结果，这有利于其在现实场景中的应用. 同理，图3 的收敛结果也照应了图2 中EEGapc的聚类高效性.

5 总结与展望

随着脑电信号数据中无标签数据的日益增加,给基于脑电信号的应用, 如脑-机接口、疾病辅助诊断、康复，甚至军事领域等, 都带来了巨大挑战. 由于现有的大部分针对脑电信号的研究及应用都集中在有监督分类方面, 而有监督的分类方法十分依赖数据中的标签信息, 所以其并不适用于处理无标签脑电信号这一新型数据. 为了解决该问题并拓展无标签脑电信号的应用领域, 提出了一种多项正则化约束的伪标签传播优化脑电信号聚类方法. 该方法主要采用了伪标签传播、脑电信号相似度邻接矩阵及标签分类器联合优化的方式实现无标签脑电信号的标签化与聚类, 并将该聚类模型转化为一个多目标优化问题, 随之提出了一种基于梯度下降策略的聚类算法EEGapc. EEGapc 聚类算法能在较短时间内收敛到局部最优, 并实现无标签脑电信号的聚类. 结合14 个真实的脑电信号数据集, 从4 个评价指标比较了8 种不同类型的时间序列聚类算法, 结果都表明了本文提出的EEGapc 算法具有最好的脑电信号聚类性能.

在未来的工作中, 可以充分利用原始脑电信号数据中有限的先验信息, 如少量的标签信息, 对提出的模型进行约束, 实现脑电信号的半监督分析, 从而进一步提高无标签脑电信号的聚类性能. 由于脑电信号是一种具有时间序列特性的生物电信号，因此,提出的聚类方法理论上也可以应用到其他基于时间序列的无监督分析领域中, 能为该领域提供一定的方法指导. 诚然, 这也可以作为未来的一个研究内容和应用方向. 另外，根据现有的研究, 针对脑电信号数据的预处理, 如时频域分析、时空域分析有助于提升脑电信号的分析性能, 因此, 其也可以作为今后的一个技术手段, 辅助脑电信号聚类算法实现性能的进一步提升.

作者贡献声明：代成龙提出了模型理论、算法思路、实验方案并撰写论文；李光辉提出指导意见，参与论文修改；李栋完成实验数据处理与实验分析；申佳华完成数据获取与实验分析；皮德常提出指导意见，参与论文修改.