利用双通道激光雷达验证低信噪比反演算法*

林瑞奇，郭 磐，陈 和，陈思颖，张寅超，郑熠泽

（北京理工大学 光电学院，北京 100081）

0 引 言

相干测风激光雷达（LiDAR）已经广泛应用在风场遥感中，并为风力发电、航空运输、气象观测提供长期可靠的实时数据［1，2］。相干测风雷达系统首先利用平衡探测器将混频后的回波信号转换为电信号，再经过数字化仪、距离门划分和功率谱估计后，最终从功率谱中估计径向和（或）矢量风速［3］。相干测风雷达最重要的性能指标是探测距离和探测精度。随着探测距离的提高，LiDAR的信噪比（signalto-noise ratio，SNR）会逐渐降低，直至信号淹没在噪声中。这导致在低SNR区域，径向风速估计中会出现错误结果，同时正确结果的精度也会降低。

许多应用中都需要使用二维（2D）或三维（3D）的矢量风速。最常用的使用单台雷达获取3D风场的方式是使用速度方向显示（velocity-azimuth display，VAD）方式扫描，并利用多个方向上的径向结果对矢量结果进行估计［4］。由于多个方向上的信息存在一定冗余性，从存在错误数据的低SNR结果中反演出正确矢量风速估计是可能的。正弦波拟合（sine wave fitting，SWF）方法和累加功率谱函数最大值（maximum of the function of accumulated spectra，MFAS）方法都是适用于VAD扫描中的矢量风速合成方法。SWF方法首先计算径向风速估计再进行合成，又细分为直接正弦波拟合（direct SWF，DSWF）、滤波正弦波拟合（filtered SWF，FSWF）［5］、自适应迭代重加权正弦波拟合（adaptive iteratively reweighted SWF，AIRSWF）［6］等方法。DSWF方法最简单，但是受错误估计影响很大，只适用于高SNR区域。FSWF算法在理论上取得了仅利用径向风速估计能够获取的最优结果，但是计算复杂度高［7］，AIRSWF算法则兼顾了算法复杂度和低SNR性能。MFAS算法则直接从功率谱中估计矢量风速，性能最好，但是计算复杂度也最高［8］。

然而，在利用实际系统对这些算法的性能进行验证时始终存在一些问题。当利用其他系统探测的结果作为真值，例如与声波风速仪、探空雷达等的结果进行对比时，由于这些观测手段在时间和空间分辨率上都低于LiDAR，往往只能用于剔除粗大误差［9］。即使利用风塔探测数据进行对比，仍存在不同系统间的指向不同（实际探测区域不同）的问题，导致它们的结果之间不可避免地存在误差，这些误差不属于算法误差，但很难被解耦，最终导致算法的精度低于预期［10］。利用数值仿真实验对算法的精度进行分析时虽然有输入值作为真值，但由于仿真与实际探测的差异，其误差结果对实际使用的指导意义也存在局限性。

针对低SNR下数据仿真验证和其他观测设备都与实际探测结果之间存在差异的问题，本文研究开发了一种双通道的脉冲相干测风LiDAR系统，并利用其对不同数据处理算法在实际系统中的精度进行比较。这一系统在传统的单通道探测系统的基础上，添加了一路探测通道，对大气气溶胶粒子的退偏信号进行采集。由于大气粒子的退偏比通常低于0.2［11］，退偏通道的SNR远低于原通道。本文研究以原探测通道的风速估计结果作为真值，将各个算法应用在退偏通道上，以比较它们在低SNR下的性能表现。与使用其他仪器相比，使用这一双通道雷达保证了探测目标、时间和空间位置的完全一致。通过对实验数据的分析，对比了不同算法在不同SNR 下的精度和最合适的使用场景。结果对于充分利用现有系统、使用新算法提高低SNR下的数据获取效率，或在指定探测指标的前提下降低激光能量等硬件要求、实现系统小型化，都有一定意义。

1 双通道LiDAR系统

1.1 系统结构和参数

本文研究使用的系统是一种自研的相干多普勒测风LiDAR，它是在Rui X 等人研发的便携式系统的基础上改进而来的。原系统总质量轻，可以实现最大约1 km的探测距离［12］。系统通过与风塔的标定实验，验证了高SNR 下系统使用FSWF算法进行矢量风速估计的正确性。改进的内容包括使用更大能量的激光器、提高采样率至1 GHz，以及增加第二个探测通道。系统的基本参数如表1 所示，在更新了激光器和数字化仪后，系统的最大探测高度超过了2 km。系统的外观和增加了第二个探测通道的系统结构如图1所示。其中，灰色区域是在原有系统上添加的S 偏振态的回波光的探测通道。

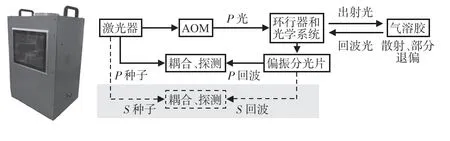
图1 自研的便携式相干测风LiDAR外观和原理

表1 改进后的相干多普勒测风LiDAR的系统参数

1.2 双通道的SNR

系统的激光光源提供P 偏振态的脉冲光，经过AOM和环行器后向外出射，在照射到大气气溶胶粒子后，发生散射。退偏振是指P 偏振态的线偏光照射在气溶胶粒子上时，后向散射光中出现了垂直于P态的分量，即S态的回波光。LiDAR后向散射信号中，S 分量的光的和P 分量的比值称为退偏比δ。气溶胶团对于特定波长λ的光的退偏比为［11］

式中 βS和βP为后向散射系数在S方向和P方向上的分量。而根据LiDAR方程，脉冲能量为Ex的系统对探测距离为R的气溶胶团作用时，接收到的回波功率为［13］

式中 ηox为光学系统传输损耗，ηTx为光学系统截断损耗，T为大气透过率，c为光速，β为后向散射系数，Ar为接收器（望远镜）的面积。因此，P 方向和S 方向上接收能量的比值和退偏比成正比

对于常见的大气气溶胶团，退偏比通常在0.2 以下，可以认为系统在S通道上的能量远小于P通道。2 个通道使用相同的平衡探测器（Thorlabs PDB460C-AC）和采集卡进行探测，因此，二者的增益比接近1，噪声的差距也很小，可以认为2个通道的SNR基本和回波信号强度成正比。

使用这一双通道雷达的S 通道作为低SNR 数据进行反演，P通道的高SNR 数据作为真值，可以对各个算法在低SNR下的精度进行评价。由于使用的是同一雷达在同一时刻发出激光，探测光束作用的粒子对两通道而言是完全相同的，也就避免了使用其他设备的测量结果作为真值时，探测对象实际上并不统一的问题。此外，也避免了将雷达与其他探测设备间的系统误差视为算法误差的可能性，非常适合对比不同的矢量风速反演算法。

2 矢量风速反演算法

2.1 VAD方法

VAD方法是使用一台雷达获取风矢量廓线最简单有效的方法，被广泛应用在测风LiDAR 中，本研究中对比的方法都是基于VAD 方法进行反演的算法。方法采用如图2所示的圆锥扫描方式［4］。

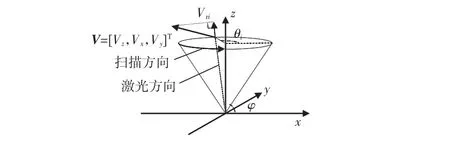
图2 VAD扫描方法示意

LiDAR以固定的俯仰角φ 进行扫描，当扫描至方位角θi（i ＝1，2，3，…，p，p≥3）时，矢量风速V与径向风速Vri满足投影关系

其中，矢量风速可以表达为V ＝［Vz，Vx，Vy］T，即由3个方向上的径向风速分量确定的矢量值。

2.2 SWF算法

在给定的V下，单个方向i上的径向风速的估计值＾Vri的条件概率密度函数由正确估计的高斯分布和错误估计的均匀分布2个部分组成［14］

式中 σg为正确估计结果的标准差，b为错误估计出现的概率，Bv为速度的搜索范围。由于各个径向的分布是独立的，所有径向风速估计的联合条件概率密度函数PDFjoint即为各个PDFi的乘积

SWF算法求解PDFjoint取得最大值时的矢量风速V 作为反演结果。依照不同的求解方法，SWF算法又细分为DSWF、FSWF和AIRSWF算法［6］。

2.2.1 DSWF算法

DSWF算法假设b为0，σg为常数，可将对V的估计简化为求下式的最小值［5］

求解取得最小值的V在解析解

由于DSWF 算法有解析解，使其具有最小的运算量。但由于假设b为0，DSWF算法在出现错误径向风速时，会出现较大的误差。

2.2.2 AIRSWF算法

AIRSWF算法是一种基于加权正弦波拟合（weighted DSWF，wDSWF）算法，并自适应迭代权值的方法。当式（7）中的各个径向有不同的权值wi时的解析解为

AIRSWF利用下述公式进行迭代［6］

式中 t为迭代次数，s（t）d和m（t）d为d（t）i的标准差和均值。迭代的初始wi均为1，终止条件为1／p。AIRSWF算法通过对偏离正弦分布的点较小的权值，能够过滤一部分错误结果，性能优于DSWF算法。由于引入了迭代，速度慢于DSWF算法，但通常迭代在数十次内就会终止，计算复杂度仍较小。

2.2.3 FSWF算法

FSWF算法认为式（6）中的σg为常数，b 不为0，且满足（1 -b）／≤b／Bv，可以将求解PDFjoint的最大值近似为求下式的最大值［5］

相比于DSWF算法，FSWF 算法过滤了径向风速估计不在区间］的径向风速对评价函数的贡献，是低SNR区域根据径向风速估计值可以取得的理论最优结果。但算法需要引入优化算法，计算速度很慢。

2.3 MFAS算法

MFAS算法是专门针对相干多普勒测风LiDAR的矢量风速合成算法，算法为多个方向上的功率谱结果建立了评价函数，直接估计矢量风速而无需计算径向风速。其评价函数为［5］

3 观测数据与算法的性能对比

3.1 观测数据

在2021年10 月，利用LiDAR 开展实验并采集了超过100000个径向上的数据。这些数据在2个通道上的SNR分布如图3所示。这里使用的SNR是用系统的频域SNR来描述的。可以看出，随着时间和大气条件变化，SNR有较大的变化，但P通道的SNR始终高于S通道，与理论分析一致。

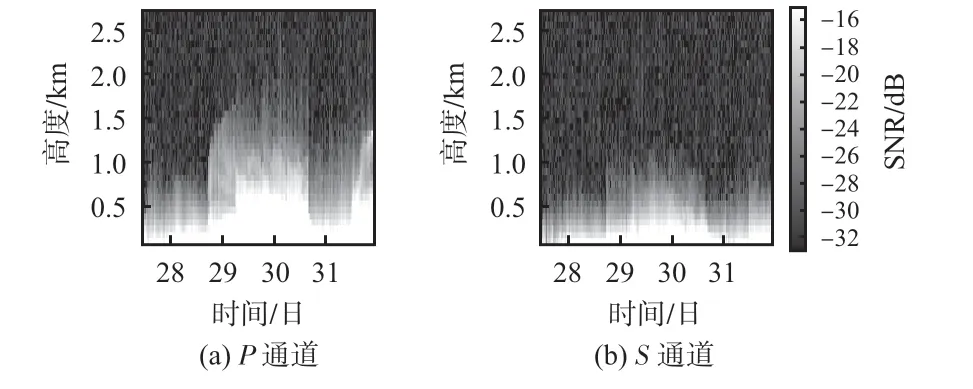
图3 P通道和S通道探测结果的SNR时空分布

为了描述系统的SNR与信号质量的关系，本文统计了不同SNR下的正确径向风速估计的标准差和占全部数据的比例，这2个参数是通过统计径向风速的分布，并根据式（5）进行拟合得到的。结果如图4 所示，当SNR在-26 dB以上时，几乎所有结果都是正确的。随着SNR的降低，正确估计的比例也快速下降，标准差也略有增大，但始终低于0.3 m／s；当SNR为-28 dB 时，有50%的径向风速估计是正确的；当SNR为-30 dB时，下降到8%；当SNR低于-32 dB时，正确数据过少导致拟合不再稳定，标准差反而降低。

图4 正确径向风速估计的标准差和占全部数据的比例随SNR的分布

3.2 低SNR下算法的精度对比

使用FSWF 算法反演P 通道的数据，并将SNR 低于-26 dB的数据过滤后作为真值。将4 种算法应用在S 通道上，并计算矢量风速估计结果与真值的差。由于差值是三维矢量，本文进一步使用其模的值作为衡量误差的标准，即统计在不同SNR 下各个算法的误差分布的质量分布。其中，SNR在-27 dB和-29 dB时，数据的统计结果非常有代表性，它们展示在图5 中；当SNR 为-27 dB时，有约13%的径向风速结果是错误的，DSWF算法已经出现了大量错误结果，此时AIRSWF 只有零星分布的误差较大的结果；当SNR为-29 dB时，AIRSWF算法的性能显著恶化，而FSWF和MFAS算法只是误差略有增大，几乎没有明显错误的结果。

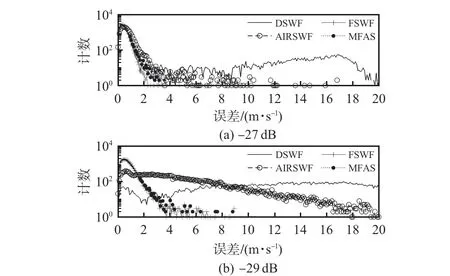
图5 SNR在-27 dB和-29 dB附近下不同算法的误差分布统计

从图5中可以看出，算法反演正确的结果。会集中在误差小于3 m／s的区域。将误差小于3 m／s的数据占全部数据的比例视为正确数据的比例，统计误差小于3 m／s 的结果的误差均值来比较各个算法的精度，并用计数降至最大值的1／10时，计数所在的误差来描述分布的展宽情况。这3个指标的结果展示在图6中。

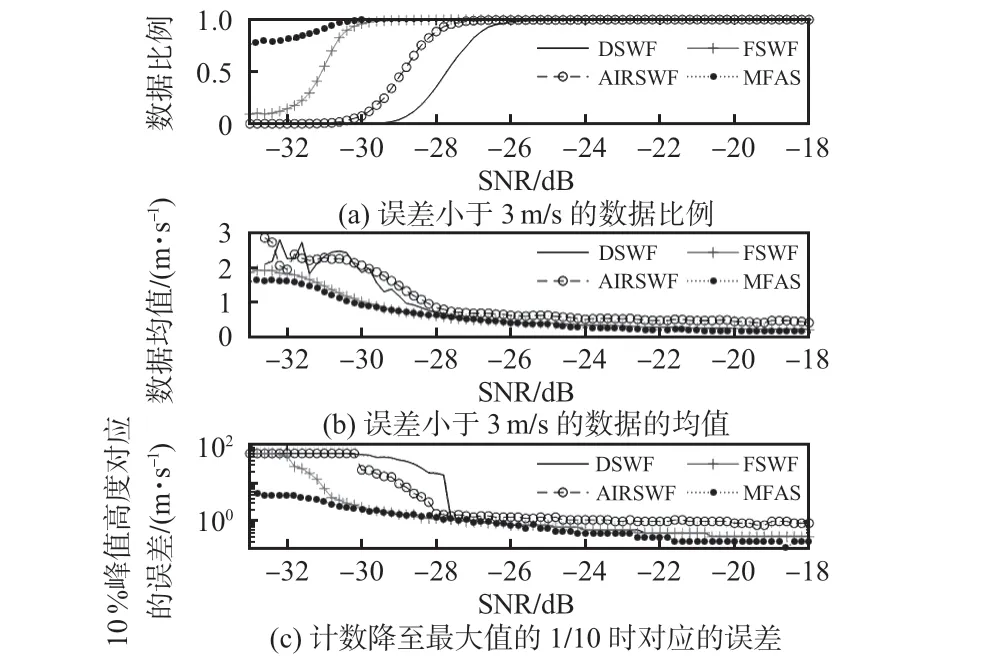
图6 不同SNR下，4 种算法的3 个指标仿真结果

从图6 中可以看出，AIRSWF 算法的性能在-26 ～-28 dB相比DSWF算法有较大的领先；当低于-28 dB 时精度和正确率都显著下降。在-28 ～-30 dB 时，FSWF 算法仍能保证结果的正确性，并且与MFAS 算法的表现非常接近；在-30 dB处，这二者的误差均值仍有约1 m／s，可以满足大部分观测的需求。当SNR 进一步下降时，虽然MFAS算法的表现好于FSWF 算法，但正确率也已经低于100%。在实际应用中，当数据的正确率低于100%时，只能利用聚类方法等数据质量控制方法对结果进一步过滤才能使用，而这些方法都需要获取大量数据后再进行处理。因此，如果是实时反演，使用MFAS算法带来的提升十分有限，但在对大量风场数据的再分析应用中，使用MFAS算法可以提供最多的有效数据和最好的精度。此外，根据双通道雷达的数据，AIRSWF算法的精度在高SNR区域略低于其他算法，误差的均值和分布宽度都略大于DSWF 和FSWF 算法，这是以往的研究中利用数值仿真没有发现的特征［6］。

3.3 算法复杂度与组合应用

算法的复杂度也是算法性能的重要一环，复杂度低的算法可以带来更快的计算速度，或是降低对硬件性能的要求。除了定性和理论的分析，本文利用一台搭载AMD R5 3600处理器的电脑，在MATLAB R2020b中进行反演，并统计各个算法反演10 000个矢量风速的用时，以比较各个算法的复杂度。

算法用时如图7 所示，可以看出，FSWF和MFAS 算法需要比AIRSWF或DSWF算法多数百倍的时间，使用AIRSWF算法在特定的SNR 区间内替换FSWF 算法可以显著降低计算量。例如，如果将对P通道的数据实时处理改用为使用DSWF、AIRSWF和FSWF算法分别处理大于-26dB，-26～-28 dB和-28～-30 dB 的数据的组合，比仅使用DSWF算法可以多获取68%的结果，比仅使用FSWF 算法节约60%的时间，比使用DSWF和FSWF算法分别处理大于-26 dB和-26～-30 dB的数据的组合也要节省36%的时间。

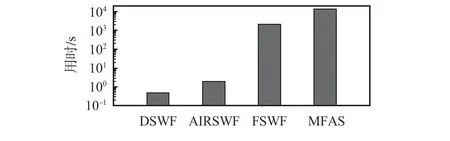
图7 反演10 000 个矢量风速的用时

4 结 论

本文使用一台双通道的脉冲相干测风LiDAR，对目前常用的矢量风速反演算法的性能进行了比较，并验证了它们在低SNR下的性能。实测数据表明：MFAS 算法性能最好，但耗时巨大，适用于对观测数据进行再分析时使用。在需要实时风廓线的应用中，AIRSWF算法可以在SNR 降低至只有约50%的径向风速是正确的情况下提供可靠的估计，FSWF算法则在仅有10%的正确径向结果时仍能提供可靠的结果。按照SNR选择合适的算法进行处理，可以显著提高LiDAR的性能表现，或降低对激光能量的需求以降低能耗或实现系统的小型化。