基于靶标的小角度结构缝平面检测算法与应用

李 斌，丁 勇，谢东辉，李登华，孙 晨

(1.南京理工大学 理学院，江苏 南京 210094； 2.宁波原水有限公司皎口水库分公司，浙江 宁波 315000； 3.南京水利科学研究院，江苏 南京 210029)

结构性裂缝的工作状态直接关系到水工建筑物的正常使用状态，其中大型面板堆石坝突出问题之一就是面板的结构性裂缝[1]。传统人工检测方式存在效率低且检测精度易受检测人员主观影响等问题，传统机器视觉裂缝识别技术存在复杂结构表面噪声干扰裂缝的识别与提取等问题[2]。基于机器视觉的精密测量技术在水利、桥梁工程等结构健康监测领域的应用越来越普遍，已成为研究热点[3-5]。徐昊等[6]设计了基于无人机采集图像的桥梁裂缝监测系统；谢文高等[7]使用水下机器人搭载摄像头采集桥梁裂缝，通过提取裂缝边缘特征计算裂缝宽度；姚冰等[8]基于数字摄影原理提出的裂缝宽度测量方法，实现在桥梁工程中精确的远距离裂缝宽度测量；刘伟等[9]通过在手机上安装激光模块测量裂缝宽度；Bal 等[10]使用红外标记物作为特征，对裂缝宽度变化进行检测。这些方法具有较高的精度，但未对倾斜摄影测量进行深入研究。

本文提出一种结构缝二维平面变化测量方法，并设计能够适应小角度拍摄条件下的靶标，用靶标变化代替结构缝变化进行计算。与传统结构缝宽度变化检测方式相比，该方法不需要进行繁琐的相机标定，具有测量结构缝二维平面变化、小角度倾斜摄影测量且不易受结构复杂表面噪声影响的能力。

1 靶标设计与识别

在视觉测量领域，研究人员通常采用放置靶标的方式来获取真实空间与像素空间的比例尺和一系列特征点信息。靶标作为机器视觉测量系统的重要组成部分，会在很大程度上影响机器视觉测量系统的稳定性、实时性与精确性。为解决小角度拍摄条件下的结构缝二维平面变化检测问题，和真实空间中经过透视投影后存在的圆心偏离问题[11]，本文选用可以通过交比不变性对同心圆圆心坐标进行修正的同心圆作为靶标特征点，设计了一种基于同心圆排列的适应小角度倾斜拍摄测量的靶标（图1），图1(a)为主靶标，图1(b)为副靶标，同心圆作为靶标特征点，靶标上三圆同心的为靶标主点；主同心圆各圆半径满足1∶2∶3，其余同心圆各圆的半径满足1∶2；靶标外侧的辅助线用于靶标安装。

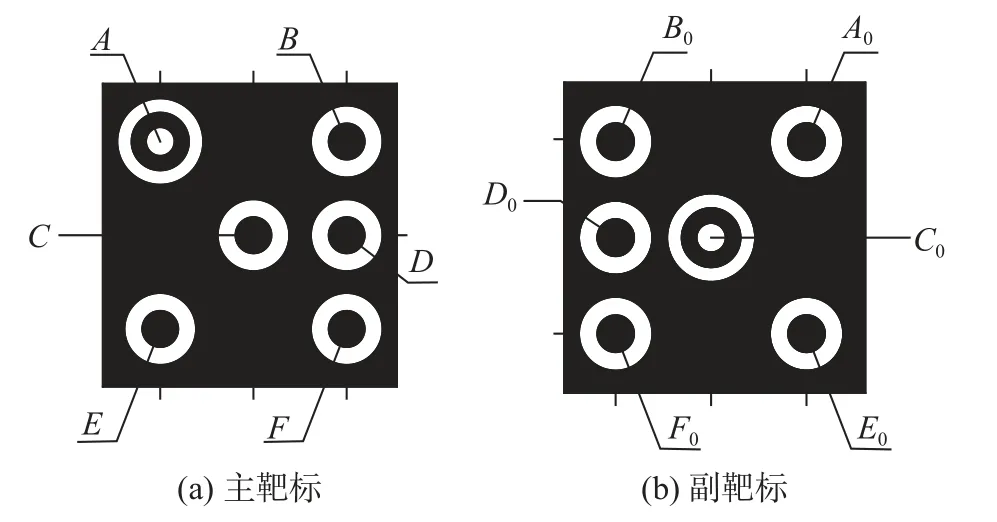
图1 靶标示意图Fig.1 Schematic diagram of target

靶标的识别分为靶标粗定位、特征提取、定位修正、靶标识别4 个步骤：首先对原始输入图像进行预处理，包括图像灰度化、双边滤波、Sobel 算子边缘检测、边缘轮廓提取；以提取的轮廓分割出若干ROI，对每个区域分别进行预处理后再进行所有轮廓信息的密度聚类；然后对每一类簇进行椭圆拟合及筛选，提取出同心圆特征，对同心圆进行圆心修正；最后确定主副靶标及主点并对特征点编号。

1.1 预处理

图像预处理的目的是分割出含有靶标的候选区域。首先对输入图像进行灰度化处理，根据加权平均公式计算得到灰度图像，可以在保留图像信息的同时减小计算量。原始图像含有噪声，噪声会影响算法的效果与效率，需对图像进行降噪处理。双边滤波器使用2 个高斯滤波器，比高斯滤波器多考虑了像素值的相似度，可以在保留图像边缘信息的同时消除噪声。Otsu 算法通过计算前景和背景的最大类间方差得到阈值。然后对二值化图像用Sobel 算子进行卷积获得边缘图像。最后将边缘点连接形成边缘链，筛除短边缘链及无序边缘链后，对边缘链求最小外接矩形，分割为若干个感兴趣区域。预处理效果如图2 所示。

图2 预处理过程Fig.2 Preprocessing process

1.2 亚像素边缘特征提取

对子区域重新预处理后得到的边缘信息使用密度聚类算法[12]，将紧密相连的点划分为同一簇，使用最小二乘法对每一簇进行椭圆拟合。椭圆的一般方程为：

式中：(x0,y0)为椭圆中心；a、b分别为椭圆长半轴、短半轴； θ为椭圆长轴与x轴夹角。可根据椭圆的几何参数筛选误差较大和不完整的椭圆，最后通过圆心距来进一步筛选同心椭圆：

式中：w、h分别为图像宽和高；r=max(a,b)；R、l、S分别为椭圆圆度、周长和面积； ξ1、 ξ2为阈值；oin、oout为内外椭圆圆心。通过设置合适的 ξ1、 ξ2将密度聚类算法拟合出的椭圆集进行剔除，得到同心圆的圆心集并确定主副靶标的主点A、C0。

上述方法筛选得到的椭圆参数由边缘的像素级坐标拟合得到，不能满足高精度要求。本文使用双线性插值法来提取亚像素级边缘坐标。设椭圆轮廓上任意一点p(x,y)法向量→n=(2Ax+By+D,2Cy+Bx+E)，沿灰度梯度方向在边缘点两侧各取t个点，用双线性插值法计算这些点的灰度值，并取向前后向差分的平均值作为对应点在法线上的灰度导数：

式中：fi为ti的灰度值；为ti的灰度导数。假设为极值时，极值点为μ，则像素点p对应的亚像素坐标为：

1.3 圆心修正

经过透视投影后，真实空间中圆的圆心与投影后的圆心存在圆心偏差，且在真实空间中同心的圆投影后的圆心位于同一条直线上[11]。如图3(b)所示，ob、os分别为大小圆投影后在图像上的圆心，o′为同心圆圆心o的真实投影。直线lt过ob、os两点交同心圆于点a′、b′、c′、d′，直线lt在空间中对应ls，其在真实空间中与同心圆交于a、b、c、d四点。由交比不变性可得：

图3 同心圆投影示意及修正效果Fig.3 Concentric circle projection diagram and correction effect

式中：Rb、Rs分别为大、小圆半径。联立求解上述方程，可得到同心圆的圆心在图像中的真实投影位置。

采用模板同心圆的半径分别为2 、4 cm，对上述同心圆圆心修正方法进行校验，修正后的圆心使用大的十字标记。试验结果显示大小圆的圆心均发生了不同程度的偏心，使用上述方法修正后的圆心重合于真实圆心标记中心（见图3(c)）。

完成了系统的软硬件设计后，选取一个蔬菜温室大棚进行了实际安装与测试，对该系统的软件和硬件进行了测试，硬件测试是测试物联网智能节点和底层模块是否能够正常工作，软件测试是测试该系统是否能实现远程监测和自动控制。经测试，检测终端将数据传往云服务器大约在1s左右，该系统稳定可靠，准确性高，将无线自组织网络和NB-IOT网络连接成功后，进行现场数据采集并远程传输，并自动控制设备使大棚环境处于最佳状态，NBIOT网络连接测试和监控软件运行界面如图7和图8所示。

1.4 靶标识别

使用上述方法修正后的一组同心圆圆心集合，通过几何约束确定主副靶标。由图1 可得：

式中：M(x,y)、N(x,y)、P(x,y)分别为AB、BE、BF的中点坐标；η为中点偏离阈值；λ为斜率偏离阈值。以已知主点为基准及几何约束条件确定主副靶标及各特征点。

2 结构缝二维平面变化测量方法

本文依据结构缝变化等效物理模型，即将结构缝的变化等效为两块刚体之间的相对变化，将结构缝变化测量转化为采用机器视觉的方式对固定于结构缝两侧的主副靶标的识别与计算。如图4 所示，通过辅助线将2 个靶标平行固定至结构缝两侧，将D、D0两点间的变化量等效为结构缝的变化量。

图4 结构缝二维变化等效物理模型示意Fig.4 Schematic diagram of equivalent physical model of two-dimensional change of structural joints

利用特征点连接直线AE、BF、AB、EF确定图像上两个正交的灭点V1、V2[13]，以D为坐标原点，DV1为x轴，DV2为y轴在图像中建立坐标系，对图像上任意点，其坐标为灭点V1、V2与该点连线到x、y轴的交点坐标(图5)，该方法可补偿透视投影对坐标系的影响。

图5 等效坐标系Fig.5 Equivalent coordinate system

结构缝二维变化计算方法：

（1） 以D点为坐标原点，DV1、DV2分别为x轴和y轴建立如图5 所示的坐标系。

（2） 连接灭点V1、V2和副靶标各点，其连线与x、y轴交于K、G等点。

（3） 计算C、D、K、L，G、B、H、D两组点在图像中的交比值为r1、r2。

（4） 已知世界坐标系下CD=BD=DF=D0B0=D0C0=D0F0=d，根据交比不变性原理可以推导出

（5） 获取另外一张图像并重复步骤（1）～（4），将2 张图片计算的DH、DK分别相减即可得裂缝平面的二维变化。

3 室内验证试验及结果分析

基于上述结构缝二维平面变化计算方法，利用python 语言编制程序，进行拍摄距离变化下的精度试验、多种拍摄条件下的测量精度试验和固定结构缝在各拍摄角度下的精度试验。试验设备：分辨率为2 400 万像素的NikonD750 作为图像采集设备，双轴滑台作为试验平台，电子千分表作为参照标准。

3.1 拍摄距离变化下的精度试验

2 个靶标置于双轴滑台平台上，使用2 个电子千分表记录x、y方向的真实位移。试验装置见图6(a)，固定每组的拍摄距离，控制滑台在x或y方向上每次移动1 mm 模拟结构缝变化，采集图像，将图像计算结果与初始图像计算结果进行比较，验证本文算法在不同拍摄距离下的精度。L代表靶标C、D间平均单位像素对应的真实距离（mm）（平均单位像素对应的真实距离等同于mm/pix，pix 为像素），综合考虑了拍摄距离和焦距的影响。试验结果如图7 所示，L小于0.20 mm/pix 时测量误差小于0.25 mm，误差会随L的增大而增大。

图6 试验装置及其示意图Fig.6 Test device and schematic diagram

图7 不同拍摄距离下测量误差Fig.7 Measurement error diagram under different shooting distances

3.2 多种拍摄角度下的测量精度试验

使用上述方法，固定每组的拍摄角度，测试多组拍摄角度，验证本文算法在不同倾角拍摄下的精度。试验结果如图8 所示，本次试验中L为0.07 mm/pix，在10 mm 内x方向最大测量误差为0.091 mm，y方向最大测量误差为0.096 mm。

图8 不同拍摄角度下测量误差Fig.8 Measurement error diagram under different shooting angles

3.3 角度变化条件下测量重复性试验

如图6(b)，将靶标固定于木板上，木板从垂直拍摄开始依次转动10°，将每次图像计算结果与90°拍摄条件下计算结果进行比较，试验结果见表1。本次试验中L均值小于0.09 mm/pix，光轴与拍摄物平面之间的夹角从90°变化到 30°时，x方向计算误差小于0.10 mm，20°时x方向测量误差最大为0.214 mm。光轴与拍摄物平面之间的夹角从90°变化到20°时，y方向测量误差均小于0.03 mm。

表1 拍摄角度与测量精度Tab.1 Shooting angle and measurement accuracy

4 现场试验

为验证本文方法在实际工程中的可行性，将其用于浙江省宁波市某大二型混凝土重力坝坝顶结构缝变化监测中。该水库大坝全长407 m，每个坝段长20 m。选用2、3、4 坝段之间的结构缝作为监测对象（图9）。试验采用DH-SD-8A2440V-NBHL 网络球型摄像机，具有56 倍光学变焦、400 万像素及本文靶标。将球形摄像机固定在闸门启闭室外墙上（图10）。使用水平尺将靶标如图4 方式固定在结构缝两侧（图11）。

图9 监测点Fig.9 Monitoring points

图10 球型摄像机Fig.10 Spherical camera

图11 测点图像采集示意Fig.11 Schematic diagram of measuring point image acquisition

测点处结构缝裸露部分宽度首次人工测量值分别为17.21 和18.75 mm。使用本文方法和人工测量方法对2 个测点进行为期1 个月的监测，并以4 月13 日测量值为基准得到相对变化量测量图，如图12 所示。1、2 号测点C、D间L均值分别为0.11 和0.21 mm/pix。1 号测点x、y方向误差均小于0.15 mm，2 号测点x、y方向误差均小于0.25 mm。2 号测点的误差相对1 号测点更大的主要原因是L更大，但精度均在0.25 mm 以内，满足规范0.50 mm的精度要求[14]。

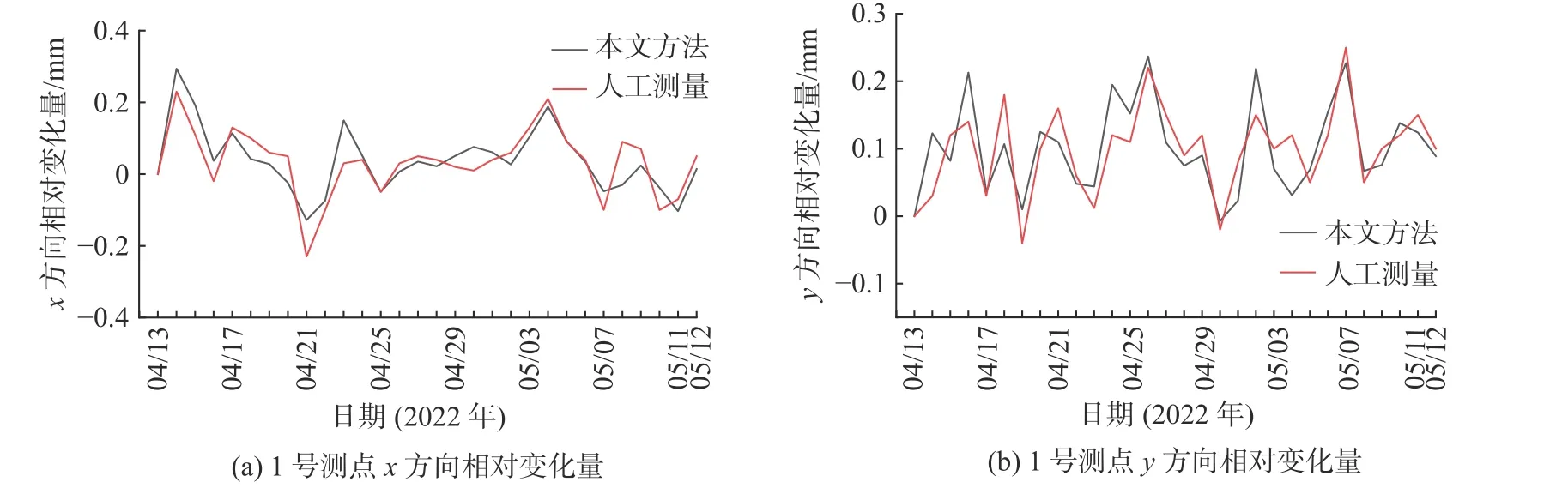
图12 测点数据Fig.12 Data of measuring points

5 结 语

本文针对现有结构缝变化测量技术存在的不足，结合图像处理技术，提出了一种适应小角度拍摄条件下的结构缝二维平面变化测量技术，为实现小角度拍摄条件下的结构缝变化测量，研发了一种适应于小角度测量的靶标。该靶标由同心圆排列组成，结构简单，整体美观。针对设计靶标所研发的测量算法，可实现小角度拍摄条件下对结构缝平面x、y方向的变化测量。室内模拟试验表明：在拍摄角度为90°～30°时，本文算法的测量误差不会随拍摄角度的变化而增大，测量误差始终小于0.10 mm。现场试验表明：使用本文方法及靶标可以实现结构缝x、y方向的变化量测量，且在L小于0.20 mm/pix 时测量精度在0.25 mm 以内，满足水工建筑物大范围监测需求，具有工程应用价值。