旱灾风险评估的减法集对势梯形模糊数随机模拟方法

沈 勇，崔 毅，陈 浩，汪 洁，周亮广，周戎星

(1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009； 2.合肥工业大学 水资源与环境系统工程研究所，安徽 合肥 230009)

干旱灾害是自然界水循环过程中的供水长期低于平均水平达到一定程度后对生态环境、经济社会产生不利影响的水文气象灾害[1-2]。随着社会经济快速发展、人口密度持续增加，水资源供需矛盾问题日益尖锐，旱灾形势日渐严峻，旱灾风险防御日显重要。其中，旱灾风险评估既是旱灾风险诊断和决策过程的难点，也是旱灾风险防御的基础工作和关键环节，近10 年来逐渐成为研究热点[3-5]。目前，旱灾风险评估方法主要有信息扩散法[6]、自助法[7]、集对分析法[8]、模糊综合评价法[9]等，其中集对分析法通过同、异、反三方面从宏观和微观层次上定性定量分析系统的不确定性，适于处理复杂性、随机性和模糊性的旱灾风险评估问题。此外，差异度系数表征集对系统微观层次上的不确定性，是确定联系数值评价结果的核心要素，其主要取值方法有特殊值法[10]、统计试验法[11]、比例取值法[12]、三角模糊数法[13]等。其中，特殊值法、统计试验法和比例取值法强调利用确定数值定量表示差异度系数，未考虑差异度系数随评价样本值变化的动态特性，将导致评价结果与实际情况偏差较大。现有的三角模糊数法提出以区间范围形式定量表示差异度系数，当隶属度为1 时对应1 个特定点值，然而，实际问题中模型参数峰值分布较为扁平[14]，此时用三角模糊数表征差异度系数的不确定性尚不够严谨，难以准确度量其取值。因此，合理有效的差异度系数取值方法亟待解决。

为此，本文针对差异度系数取值具有峰值较宽的分布特征及其随评价样本值变化的动态特性问题，在半偏减法集对势联系分量微观层次迁移的基础上，采用梯形模糊数动态取值表征差异度系数的不确定性和连续变化过程，通过随机模拟方法模拟梯形模糊数，进而得到差异度系数随评价样本值变化的动态置信区间，把梯形模糊数及其函数之间的运算转化为普通实数之间的运算，实现以置信区间形式定量描述评价结果，由此构建基于减法集对势梯形模糊数随机模拟的旱灾风险评估模型，并在宿州市开展旱灾风险动态评估的实证研究，用于分析旱灾风险的发展趋势和风险等级、判别导致旱灾风险的主要子系统，以期为区域旱灾风险防控管理提供科学依据。

1 差异度系数梯形模糊数的动态取值

联系数表达式是在集对分析理论研究基础上建立的，其中三元联系数表达式[5,15]为：

式中：a、b、c∈[0, 1]分别为同一度、差异度和对立度分量，且a+b+c=1；I∈[−1.0, 1.0]为差异度系数；J=−1 为对立度系数[16]。将旱灾风险划分为3 个等级，1～3 分别代表微旱、轻旱和重旱，此时等级标准阈值的序列数为s0j、s1j、s2j、s3j，其中s0j、s3j分别为评价等级1 级左端点、3 级右端点值，s1j、s2j分别为评价等级1 级与2 级、2 级与3 级的临界值[5,17]。根据特殊值法[10]，当评价样本值xij接近s0j、s3j时，I取极限值1.0 和−1.0；当评价样本值xij接近s1j、s2j时，I取中间值0.5 和−0.5。概而论之，差异度系数与等级标准阈值的对应关系[17]具体如图1 所示。

图1 差异度系数与等级标准阈值的对应关系Fig.1 Correspondence between difference coefficient and grade standard thresholds

由图1 可知：以s0j、s3j对应的差异度系数作为最大值Imax和最小值Imin，由于差异度系数的2 级标准阈值区间较宽，即存在最优值区间[17]，以s1j、s2j对应的差异度系数作为最优值区间[Iopt1,Iopt2]，据此构造差异度系数梯形模糊数的静态取值I=（Imin,Iopt1,Iopt2,Imax）=（−1.0, −0.5, 0.5, 1.0）。然而，实际问题中差异度系数具有随评价样本值变化的动态特性，此时用传统上的确定数值可能使评价结果产生较大误差，故需根据所论集对事件的评价样本值构造差异度系数梯形模糊数的动态取值。

从偏联系数[18]联系分量微观层次上迁移的观点看，假定当前的a原先位于b层次上，是从b层次正向转化而来，所以用a+b作分母，a作分子，分式a/(a+b)作为正向转化率；同理，假定当前的c原先位于b层次上，是从b层次负向转化而来，所以用b+c作分母，c作分子，分式c/(b+c)作为负向转化率，由此得到半偏减法集对势[5,19]：

根据式（1）可证明s(u)∈[−1.0, 1.0]，故可按照“均分原则”[10,19]划分相应区间及态势，即反势（[−1.0,−0.6)）、偏反势（[−0.6, −0.2)）、均势（[−0.2, 0.2]）、偏同势（(0.2, 0.6]）和同势（(0.6, 1.0]）。

进一步分析“同”“异”“反”三者之间的相互影响，当“异”向“反”转化达到一定程度时，“反”开始有先向“异”转化进而再向“同”转化的趋势；同理，当“异”向“同”转化达到一定程度时，“同”开始有先向“异”转化进而再向“反”转化的趋势。基于上述半偏减法集对势转化思想[20]，提出“I”最可能值的分化区间，具体如图2 所示。

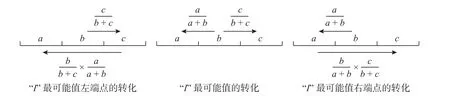
图2 “I”最可能值及左右两端点的转化Fig.2 The most probable value of “I” and the transformation of left and right end points

根据上述转化过程，构造差异度系数梯形模糊数的动态取值：

式中：l1、l2、l3和l4分别为梯形模糊变量I的最小可能值、最可能值的左端点、最可能值的右端点和最大可能值[21-22]。其中，最小可能值−c/(b+c)表示b负向发展的最大可能转化率，最大可能值a/(a+b)表示b正向发展的最大可能转化率，取值同三角模糊数一致[20-23]。最可能值的左、右端点是根据a/(a+b)−c/(b+c)的分化区间所得，其物理含义为：b先以负向发展的最大可能转化率−c/(b+c)向c中转化，此时转化后的对立度分量上包含此前b未转化到c中的部分不确定量，这部分不确定量有向a转化的趋势，其正向发展转化率为b/(b+c)×a/(a+b)，据此提出最可能值的左端点为−c/(b+c)+b/(b+c)×a/(a+b)；同理，b先以正向发展的最大可能转化率a/(a+b)向a中转化，此时转化后的同一度分量上包含此前b未转化到a中的部分不确定量，这部分不确定量有向c转化的趋势，其负向发展转化率为−b/(a+b)×c/(b+c)，据此提出最可能值的右端点为a/(a+b)−b/(a+b)×c/(b+c)。此外，在隶属度函数图中，最小可能值和最大可能值的隶属度为0，最可能值的左、右端点隶属度为1；然而，当a=0 或c=0 时，梯形模糊数为I=(−c/(b+c),c/(b+c), −c/(b+c), 0)和I=(0,a/(a+b),a/(a+b),a/(a+b))，隶属度函数图变成了直角三角形，分化了左、右端点及其附近的大量可能值，提高了最小可能值、最大可能值及其附近值出现的可能性，符合所论集对事件的实际变化情况，具体如图3 所示。

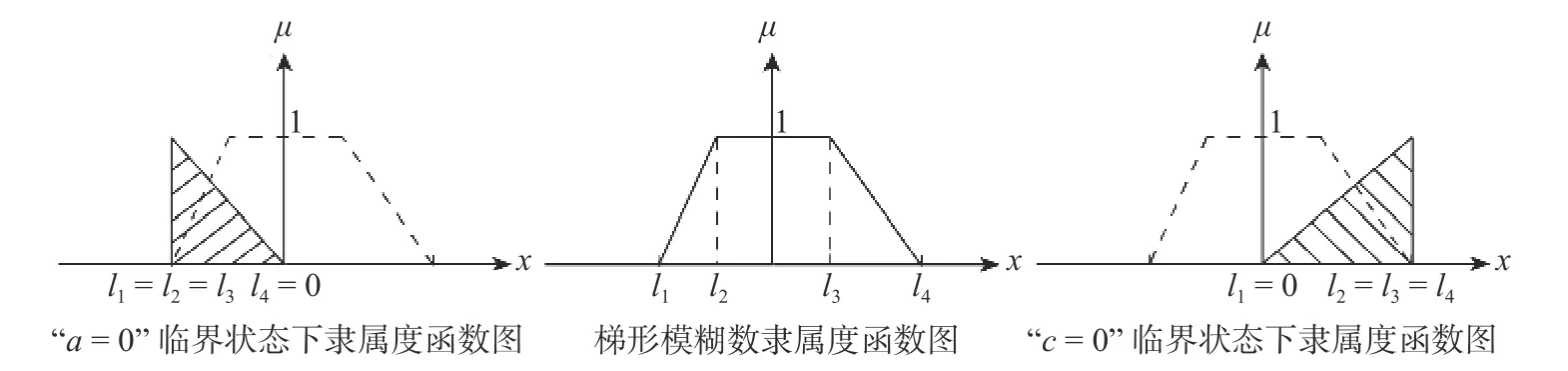
图3 梯形模糊数及两种临界状态下隶属度函数图Fig.3 Trapezoidal fuzzy number and membership function diagram under two critical states

2 构建基于减法集对势梯形模糊数随机模拟的旱灾风险评估模型

构建基于减法集对势梯形模糊数随机模拟的旱灾风险评估模型，包括以下7 个步骤：

步骤1：建立旱灾风险评价指标体系和评价等级标准。通过致灾因子危险性、承灾体的暴露性、承灾体的灾损敏感性和抗旱能力组成旱灾风险系统结构[5]，并结合研究区域的实地调研以及专家意见、文献调查，建立旱灾风险评价指标体系{xj|j=1, 2, …,nj}、评价指标样本集{xij|i=1, 2, …,ni;j=1, 2, …,nj}[5,24]。其中，xj为第j个评价指标，nj为评价指标数；xij为样本i指标j的评价样本值，ni为评价样本数目。另外，不失一般性，本文将旱灾风险划分为3 个等级，k=1, 2, 3（同图1 分析），则评价等级标准为{skj|k=1, 2, 3;j=1, 2, …,nj}[25]。

步骤2：计算旱灾风险系统联系数值及其评价等级值。根据文献[5]中公式（1）～（6）计算出评价单指标值联系数，对其加权可得旱灾风险评价样本i的联系数ui[20,23]，

式中：vik为联系数ui的联系分量，vijk为评价指标值联系分量；wj为评价指标j的权重，由加速遗传算法的模糊层次分析法（AGA-FAHP）确定；I、J同式（1）。

运用级别特征值法[15,20]计算旱灾风险评价样本i的等级值hi：

步骤3：随机模拟梯形模糊数。式（3）中的4 个实数l1、l2、l3和l4，满足l1≤l2≤l3≤l4，差异度系数梯形模糊数为I=(l1,l2,l3,l4)，根据梯形模糊数随机模拟公式[22]计算可能值变量I：

式中：u为在区间[0, 1]上的均匀分布随机数[15]。

步骤4：在随机模拟M组三元联系分量基础上，随机模拟N次梯形模糊数动态取值，构建可能值变量矩阵R。通过计算机程序在[0, 1]区间上随机模拟M组三元联系分量，产生均匀分布随机数a1、a2、…、aM，b1、b2、…、bM，c1、c2、…、cM，代入式（3）得到M组梯形模糊数动态取值；通过计算机程序在[0, 1]区间上随机模拟N次梯形模糊数，产生均匀分布随机数u1、u2、…、uN；将M组梯形模糊数动态取值和N个均匀分布随机数同时代入式（6），构建可能值变量矩阵R=IM×N：

步骤5：基于可能值变量矩阵R，构造差异度系数I在显著性水平α下的置信区间。将可能值变量矩阵R中M行相应的N个可能值变量I进行降序排列，根据经验累积频率的数学期望公式（8）[13,15]，结合式（9）可构造差异度系数I在显著性水平α下的置信区间[13]：

式中：Pl为N个差异度系数值从大到小排序、序号为l的经验累计频率；IINT[]为取整序号对应的差异度系数值。

步骤6：计算评价样本i的旱灾风险联系数值、评价等级值区间及期望。将式（9）结果代入式（4），得到联系数值区间，根据式（10）联系数值与评价等级值的线性转换函数[15,23]计算出评价等级值区间，再利用式（11）～（12）计算相应的联系数值期望S(ui)和评价等级值期望H(i)：

式中：ui∈[−1, 1]为评价样本i的联系数值，hi∈[1,3]为评价样本i的等级值；SINT[]为取整序号对应的联系数值；HINT[]为取整序号对应的评价等级值。

步骤7：验证本文方法的合理性和有效性。在随机模拟M组联系分量基础上，随机模拟N=10 000 次梯形模糊数动态取值，取显著性水平α=0.05[15]，计算联系数值期望S(u)与半偏减法集对势值s(u)、评价等级值期望H与级别特征值h的平均绝对误差[5,19]：

式中：M为随机模拟联系分量的次数，取10 000 时，d1、d2分别约为0.027 和0.037。随机模拟100 组联系分量，本文方法计算得到95%可能性的置信区间可完全包含半偏减法集对势值和级别特征值（a=0 或c=0 除外），综上说明本文方法合理有效，具体如图4 所示。

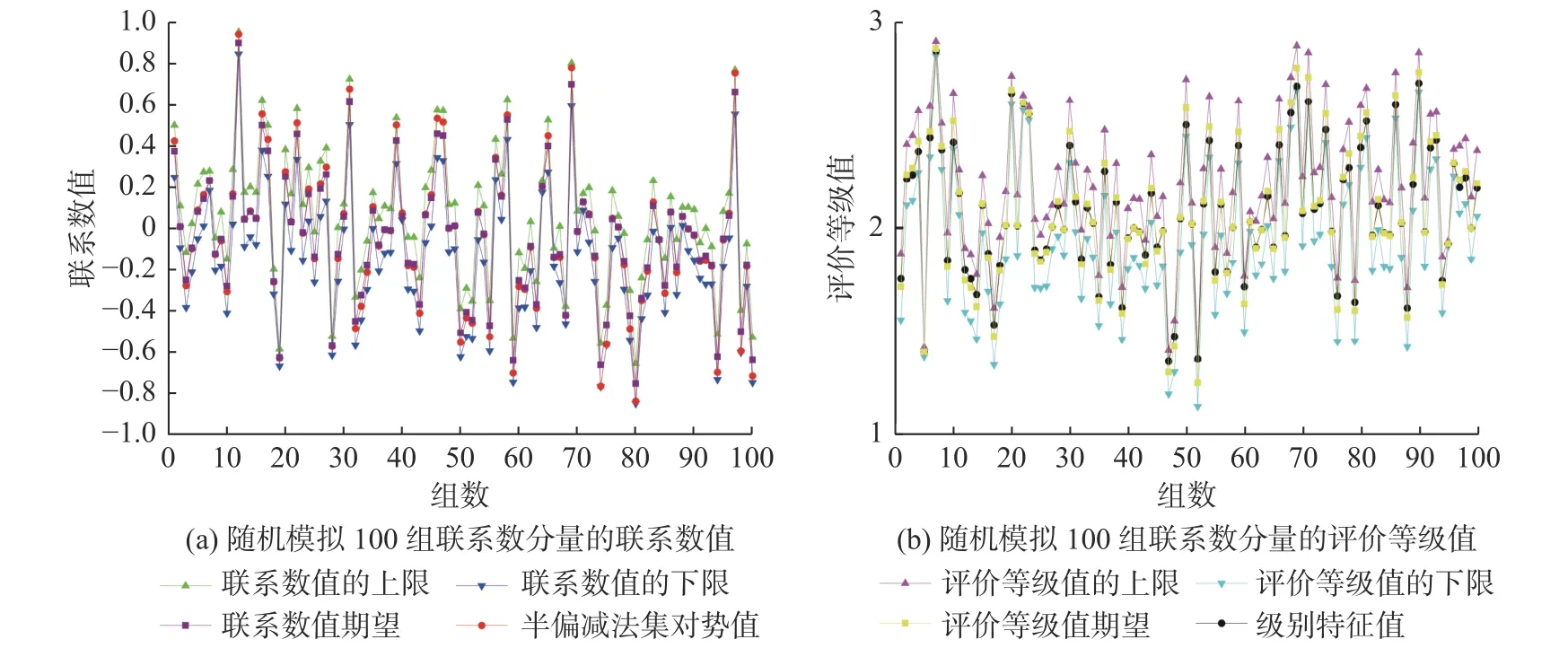
图4 随机模拟100 组联系分量的联系数值和评价等级值Fig.4 Connection values and evaluation level values of 100 sets of connection components in random simulation

3 实证研究

宿州市位于安徽省淮北地区，地处黄淮海平原南侧，属于北亚热带与温暖带的过渡地带，为半湿润半干旱季风气候区，降水时空分布不均匀，旱灾发生频率高、历时长和范围广[26]。因此，本文选择宿州市进行区域旱灾风险动态评估的实证研究，基于减法集对势梯形模糊数随机模拟的旱灾风险评估模型，构造差异度系数随评价样本值变化的动态置信区间，进而得到以置信区间形式定量描述的评价结果，并与半偏减法集对势、级别特征值法作对比分析，验证本文方法的合理性和有效性，以期为区域旱灾风险评估管理提供科学依据。

基于区域灾害系统论，旱灾风险系统可分为危险性、暴露性、灾损敏感性和抗旱能力4 个子系统[1,24]，根据《安徽省统计年鉴》（2007—2017）、《安徽省土壤田间持水量测定与分析》（2013）和《砀山县土壤熵情特点及对策》（2013）统计评价指标样本数据，引用文献[5]中旱灾风险评价指标体系、评价等级标准及权重，同时结合文献[5]中公式（1）～（6），将其计算结果代入式（4）可得宿州市2007—2017 旱灾风险系统和各子系统联系分量，经式（3）得到梯形模糊数动态取值，再依据式（6）～（9）计算出差异度系数的动态置信区间，代入式（4）、（10）～（12）得到宿州市旱灾风险系统和各子系统的联系数值、评价等级值区间及期望，同时，利用式（2）、（5）分别计算相应的半偏减法集对势值和级别特征值作对比分析，结果见表1、表2 和图5。

表1 基于梯形模糊数静态取值随机模拟的宿州市旱灾风险联系数值及评价等级值Tab.1 Connection number and evaluation grade value of drought risk in Suzhou City based on random simulation of static value of trapezoidal fuzzy number

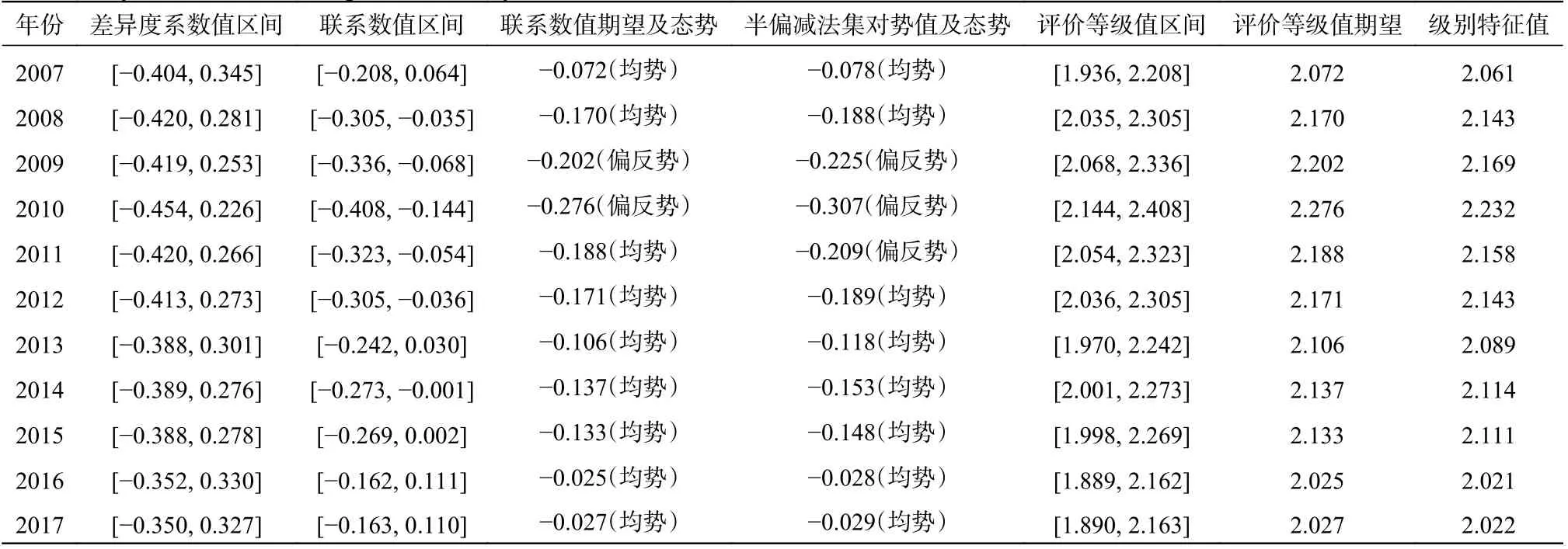
表2 基于梯形模糊数动态取值随机模拟的宿州市旱灾风险联系数值、态势及评价等级值Tab.2 Connection number, situation, and evaluation grade value of drought risk in Suzhou City based on random simulation of dynamic value of trapezoidal fuzzy number

图5 宿州市2007—2017 年旱灾风险联系数值及评价等级值Fig.5 Connection number and evaluation grade value of drought risk in Suzhou City from 2007 to 2017

由表1、表2 和图5 可知：方法一，基于差异度系数与等级标准阈值的对应关系具体定量梯形模糊数，是一种静态取值，随机模拟仅能得到唯一且固定范围的静态置信区间（I∈[−0.803, 0.806]），包含了许多不符合实际变化情况的数值，区间范围模糊宽泛；方法二，基于半偏减法集对势联系分量微观层次迁移的物理含义定性定量梯形模糊数，是一种动态取值，随机模拟得到随评价样本值变化的动态置信区间，符合实际变化情况，区间范围精确窄小。显然可见，方法二比方法一进一步精准量化了差异度系数的不确定性和连续变化过程，克服了传统上用确定数值对相关不确定性问题进行综合评价的局限性，确保了评价结果的合理性和可靠性。可见，本文方法有利于动态分析，符合实际变化情况，能准确客观地评估区域旱灾风险的发展趋势和风险等级。

从时间尺度上看：宿州市2007—2017 年旱灾风险联系数值期望和半偏减法集对势值的态势评价结果基本一致，其中2007—2010 年负向发展趋势强度增大，2011—2017 年负向发展趋势强度降低，本文方法判别出2009、2010 年处于偏反势，而半偏减法集对势判别出2009、2010 和2011 年处于偏反势，说明本文方法评价结果合理准确；宿州市2007—2017 年旱灾风险评价等级值期望和级别特征值均长期高于2 级，位于轻旱和重旱之间，处于偏旱状态；对比发现，宿州市2010 年旱灾风险最大，联系数值（评价等级值）上下限及期望为所有年份中最小（大）。总体而言，宿州市2007—2017 年旱灾风险整体波动幅度较小，有向好发展的趋势。

为进一步准确和直观地判别导致宿州市旱灾风险的主要子系统，将上述各子系统计算结果进行绘制，见图6 和7。

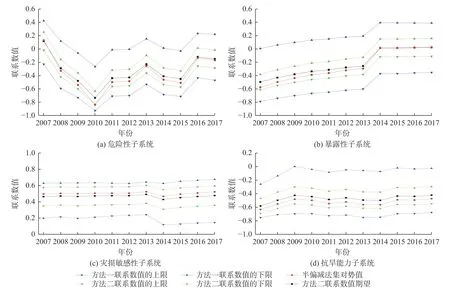
图6 宿州市2007—2017 年旱灾风险各子系统联系数值Fig.6 Connection number of each subsystem in the drought risk of Suzhou City from 2007 to 2017

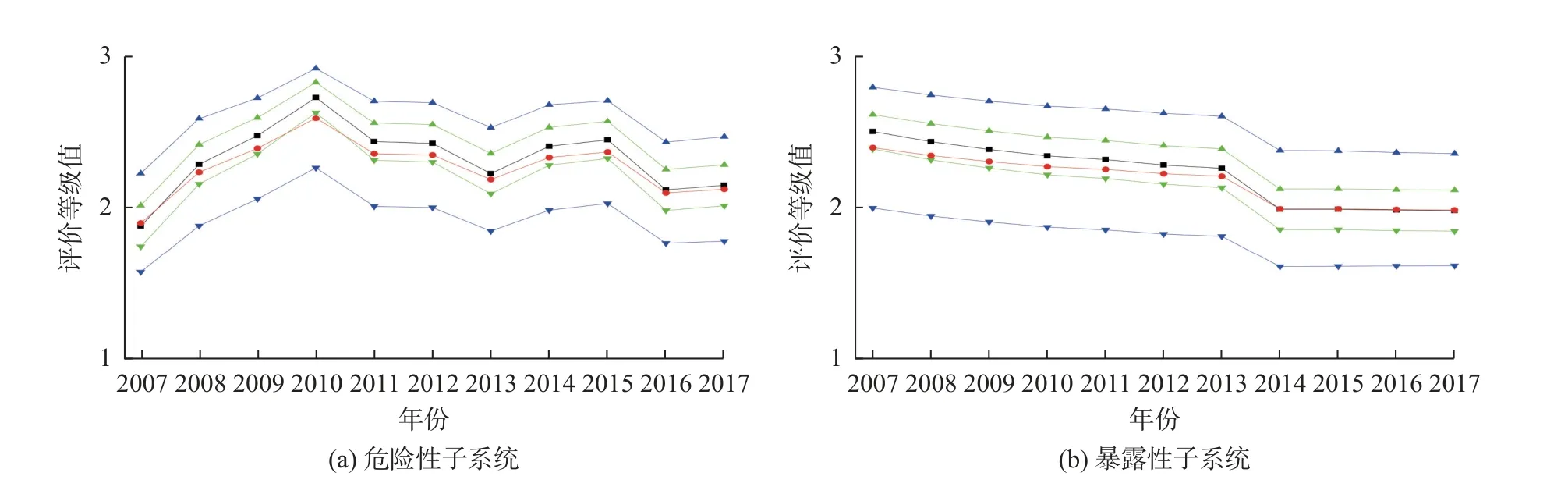
图7 宿州市2007—2017 年旱灾风险各子系统评价等级值Fig.7 Evaluation grade values of each subsystem of drought risk in Suzhou City from 2007 to 2017

由图6 和7 可知：危险性子系统风险等级基本高于2 级，旱灾风险较大，其中2010 年联系数值区间及期望均处于反势，负向发展趋势强度最大，然而，半偏减法集对势值−0.834 和级别特征值2.592 没有包含在区间内，分析可知出现了a=0 的临界情况；此时，半偏减法集对势中b仅以负向发展转化率−c/(b+c)往c中转化，联系数值比实际情况偏小，从而不易被包含；同时，差异度系数随机模拟结果将集中在最小可能值附近，由此得到评价等级值的上下限比实际情况偏大，进而不易包含级别特征值，反之亦然。对比发现，宿州市旱灾风险变化趋势与危险性子系统变化趋势完全一致，据此判别危险性子系统是导致宿州市旱灾风险的主要因素，并且影响程度最大；此外，宿州市旱灾风险的波动幅度相对于危险性子系统较为平缓，说明其余3 个子系统对宿州市旱灾风险的波动幅度具有一定调控作用。分析可知，主要是由于宿州市的致灾因子与自然属性因素和生态环境因素有关，致使旱灾发生具有随机性，而且，这种随机性人为难以进行调控。

暴露性子系统从2007—2013 年偏反势过渡到2014—2017 年均势，评价等级值区间及期望呈逐年下降的趋势，旱灾风险逐年减小，说明暴露性子系统是宿州市旱灾风险有向好发展趋势的主要因素。由此可见，宿州市的社会因素和农业经济逐年不断地改善，限制了承灾体与致灾因子时空上的接触、重合，促进了暴露性子系统中的某些指标正向发展，降低了宿州市旱灾风险。

灾损敏感性子系统2007—2017 年联系数值区间及期望均处于偏同势，正向发展趋势强度平稳，评价等级值在1.4～1.7 之间波动，旱灾风险最小，说明灾损敏感性子系统是宿州市旱灾风险有向好发展趋势的主要因素。由此可见，宿州市的承灾体基本与当地自然环境因素相适应，受干旱不利影响的敏感程度较低，处于一种比较有利的状态，降低了宿州市旱灾风险。

抗旱能力子系统2007—2017 年联系数值区间及期望基本处于偏反势，负向发展趋势强度稳定，评价等级值在2.3～2.7 之间波动，旱灾风险较大，据此判别抗旱能力子系统是导致宿州市旱灾风险的主要因素。分析可知，主要是由于宿州市水库建设、农田灌溉等水利工程建设方面存在不足。

4 结 语

为进一步精准量化差异度系数的不确定性和连续变化过程，建立科学有效的旱灾风险评估方法，提出了基于减法集对势梯形模糊数随机模拟的旱灾风险评估模型。在宿州市旱灾风险动态评估中的应用表明：

（1）宿州市2007—2010 年间旱灾风险负向发展趋势强度增大，2011—2017 年间旱灾风险负向发展趋势强度降低，判别出2009、2010 年处于偏反势，其中2010 年为最危险年份；风险等级长期高于2 级，位于轻旱和重旱之间，处于偏旱状态。然而，宿州市旱灾风险整体波动幅度较小，有向好发展的趋势。

（2）对宿州市各子系统分析判别可知，危险性、抗旱能力子系统是导致宿州市旱灾风险的主要因素，暴露性、灾损敏感性子系统是宿州市旱灾风险有向好发展趋势的主要因素；其中，危险性子系统的波动幅度最大，其余3 个子系统对宿州市旱灾风险的波动幅度具有一定调控作用；此外，危险性子系统对宿州市旱灾风险影响程度最大，但致灾因子具有随机性，进而不易进行调控，此时人为主观提高宿州市抗旱能力最为有效。因此，采用兴修水库、建设灌溉系统等方式提高蓄水能力、增加生态用水比重、调节水资源空间分布和发展节水灌溉技术是改善抗旱能力子系统的有效手段，对降低宿州市旱灾风险具有重要战略意义。

（3）本文所得的宿州市旱灾风险评估结果与实际情况一致，说明减法集对势梯形模糊数随机模拟方法合理有效，不仅克服了传统上确定数值对不确定性问题进行综合评价的局限性，而且把梯形模糊数及其函数之间的运算转化为普通实数之间的运算，在旱灾风险的动态分析和定量评估中具有推广应用价值。