无源互调测试误差分布特性初探
叶 鸣,胡少光,朱 辉
(1.西安建筑科技大学 信息与控制工程学院,西安 710055;2.中国空间技术研究院西安分院,西安 710000;3.福州博讯通电子有限公司,福州 350025)
0 引言
随着卫星通信、移动通信的持续发展,无源互调(passive intermodulation,PIM)效应引起的干扰问题越来越受关注[1-2]。传统意义上,通信系统中的无源器件一般被视为线性器件;但当同时向无源器件馈入两个及以上载波时,如果载波功率足够大且无源器件存在材料、工艺、装配等方面的缺陷所致的非线性时,就会产生无源互调效应。从频域响应角度,PIM效应通常可表述为:当同时施加两路载频信号(频率分别为f1和f2)给无源器件时,器件输出端除了有f1和f2信号外,还会有它们的线性组合产物mf1±nf2(m、n为整数,比如2f1-f2),这些新产生的信号即被称为PIM产物。当然,多于2路载频的情形也会产生PIM产物[3],而且PIM产物数量更多。当PIM信号落入接收带形成干扰时,称为PIM干扰。近年来,由于产业需求的推动,PIM问题的研究在物理机制、建模仿真、弱互调检测[4]、高低温互调检测[5]、互调源[6]等多个方面均取得了较大的进展[7-8]。
无源互调测试是PIM机理研究、产品PIM指标验证等必不可少的环节。早期,PIM测试的推荐性标准是IEC-62037[9]。2020年底,ITU针对移动通信天线的PIM测试推出了ITU-T K.149[10]。文献[7]对近年来的PIM测试技术研究进展进行了很好的综述。文献[4]提出了一种基于对消技术的弱互调测试方法。文献[8]指出当前的PIM测试存在着载波功率偏小、接收机动态范围有限(导致难以检测环形器等高互调电平的器件)、跨频段互调测试困难等问题并给出了相关的解决方法。常见的PIM测试系统可分为两大类:一类是使用信号源、功率放大器、频谱仪等常规微波仪器设备搭建的分立式测试系统[2],这类系统的优势是可以灵活组合,提高了设备利用率,在星载产品PIM测试领域应用广泛;另一类是集成化的专用PIM分析仪,比如文献[11][12]中使用的国产PIM分析仪、文献[13][14][15]中使用的进口PIM分析仪,这类系统的优势极大降低了对测试人员的要求,在移动通信领域中应用广泛。
目前,业界进行PIM测试误差分析时,基本上参考IEC-62037标准中给出的PIM误差图。然而,该误差图仅给出了PIM测试误差的上下边界,未能提供详细的误差分布信息。此外,国际电工委员会(international electrotechnical commission,IEC)给出的PIM误差图中使用的并非实测PIM而是真实PIM,由于真实PIM实际上得不到,这导致工程实践中往往只能以实测PIM代替真实PIM来进行误差估计。这些问题的存在阻碍了PIM测试误差的精细化分析。
为克服这些问题,本文基于矢量信号合成理论和蒙特卡罗模拟方法,对PIM测试误差的分布特性进行了理论和实验研究,给出了更方便工程实践使用的PIM误差图,以期为PIM测试技术的进一步发展提供参考。
1 PIM测试误差理论及验证
1.1 PIM测试误差理论
在工程实践中,实测PIM值实际上是待测件PIM信号与PIM测试系统自身残余互调信号的矢量合成信号。因此,待测件PIM信号相对于测试系统残余PIM信号的大小以及两者相位差均会影响PIM测试结果,本文假设残余互调电压信号如式(1)所列。
Vr=V1cos(ωt+φ1)
(1)
式(1)中,Vr是残余互调电压幅度,ω是互调信号的角频率,t是时间,φ1是残余互调电压信号相位,假设待测互调电压信号如式(2)所列。
Vd=V2cos(ωt+φ2)
(2)
式(2)中,V2是待测互调电压幅度,φ2是待测互调电压信号相位。实际测得的PIM电压信号如式(3)所列。
Vt=Vr+Vd
(3)
将式(1)和式(2)代入式(3)并经一系列数学处理后可得,如式(4)所列。
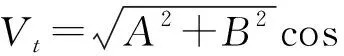
(4)
式(4)中:
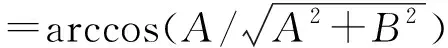
这里,Δφ=φ2-φ1。按照PIM测试领域的惯例,测试结果通常表示为以dBm为单位的功率形式。因此,以dBm为单位的系统残余互调电平如式(5)所列。
(5)
式(5)中,Z0为系统特征阻抗,通常取值50Ω;类似地,以dBm为单位的待测互调电平如式(6)所列。
(6)
以dBm为单位的实测互调电平如式(7)所列。
Pt,dBm=30+10log10[(A2+B2)/(2Z0)]
(7)
以dB为单位表示待测件PIM信号相对于测试系统残余PIM信号的大小(此即PIM行业内常用的PIM误差图的横坐标)如式(8)所列。
x=Pd,dBm-Pr,dBm
(8)
以dB为单位表示PIM测试误差(即PIM行业内常用的PIM误差图的纵坐标),如式(9)所列。
y=Pt,dBm-Pd,dBm
(9)
综合式(1)至式(9)并经一系列数学运算后得到如式(10)所列。
y=10log10{[1+10x/20cos(Δφ)]2+
10x/10sin2(Δφ)}-x
(10)
依据式(10)并假设不同的相位差,即可得到PIM行业常用的PIM误差图,如图1所示。PIM行业使用的PIM误差图仅给出了误差的上、下边界,也就是图1中相位差为0°、180°时的误差曲线。
由于目前的PIM测试通常不考虑相位问题,换言之,式(10)中的相位差Δφ是随机的。假设相位差Δφ服从均匀随机分布,采用蒙特卡罗方法对不同x值时PIM测试误差的分布进行了模拟(采样总数为10000次),结果如图2所示。当x值较小时(亦即待测互调电平与系统残余互调电平较为接近时),PIM测试误差呈现明显的非对称分布,且PIM测试误差越正,其发生概率越大;当x值逐渐增大时,PIM测试误差分布的对称性逐渐显著。从PIM测试误差的分布范围来看,误差分散性随着x值增大而减小,这意味着残余互调电平相对于待测互调越小时,测试结果的一致性越好。
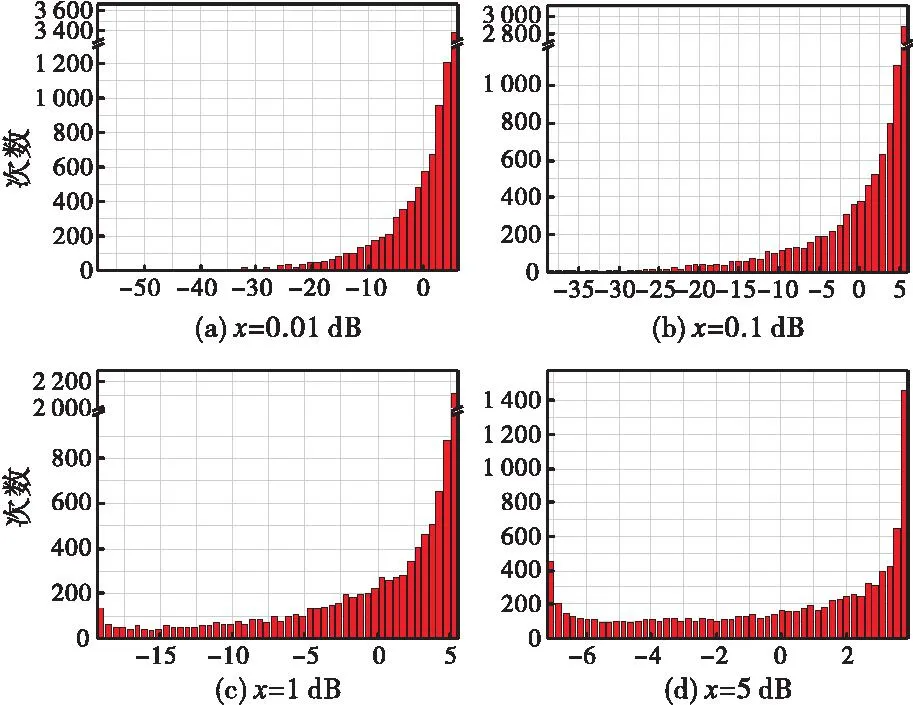
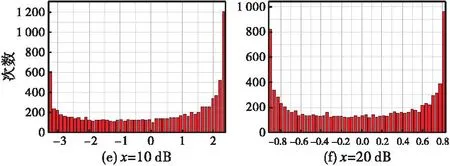
图2 依据式(10)通过蒙特卡罗模拟得到的PIM误差分布Fig.2 Simulated distribution of PIM error using Monte Carlo method and Eq.(10)
图2所示的PIM测试误差分布特性可以从如图3所示的计算结果予以解释。当x值较小,相位差为180°附近时,PIM测试误差相对0°附近的情形变化更剧烈,意味着PIM误差对相位差非常敏感。换言之,PIM误差靠近图1所示PIM误差图的下边界的概率较小,此时PIM误差分布将具有较为显著的非对称性,如图2(a)所示;而当x值较大,在相位差为180°附近时,PIM测试误差相对变化平缓,与相位差为0°附近时的变化趋势接近,此时PIM误差分布将具有较为显著的对称性,如图2(f)所示。
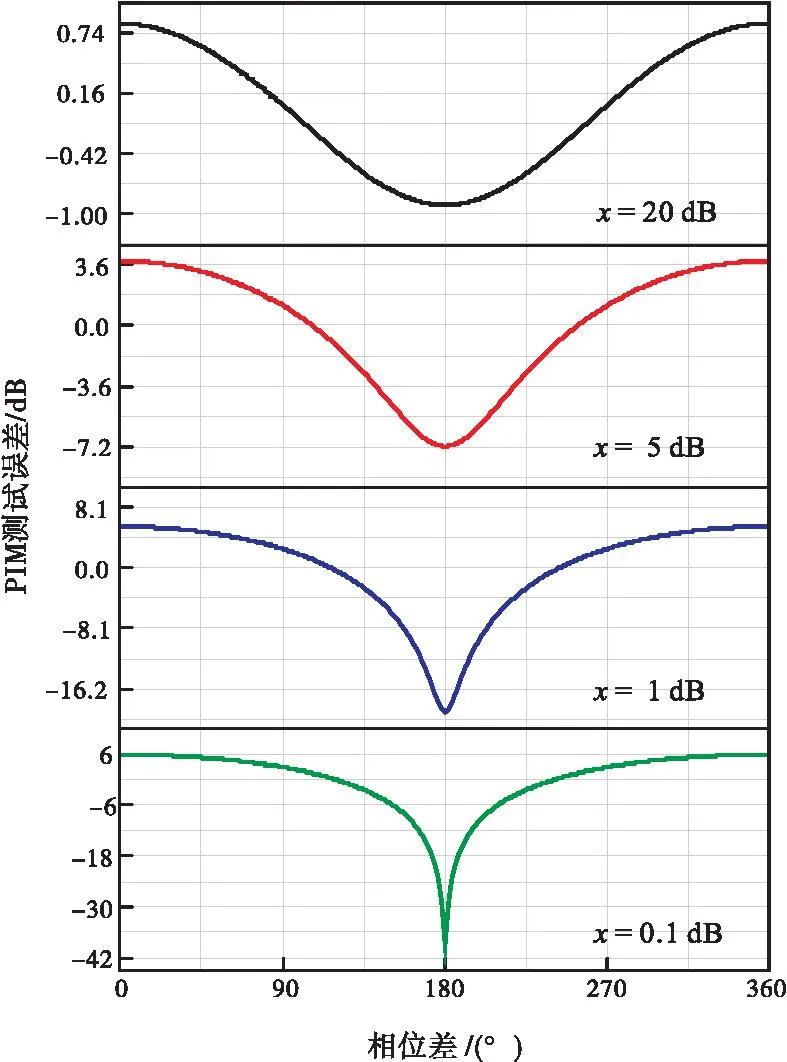
图3 依据式(10)计算得到的PIM误差随相位差的变化Fig.3 Calculated dependence of PIM error on phase difference according to Eq.(10)
1.2 PIM测试误差的初步验证
基于双通道信号源、耦合器和频谱仪搭建了如图4所示的测试系统。信号源2号端口用于模拟测试系统残余互调信号,1号端口则用于模拟待测件互调信号。实验中,保持信号源2号端口输出功率为-40dBm不变(若实验条件允许,可使用更小功率),其相位也保持不变。通过调节信号源1号端口的输出功率,可以模拟不同x值的场景。相位的随机性是通过不断重复开关信号源1号端口实现的(2号端口始终开启),重复开关约200次,得到了如图5所示的结果,从PIM误差分散范围和分布形状两方面来看,实验结果与理论结果基本吻合。由于实验次数相对较少,分布形态与图2相比略有差异。

图4 模拟实验所用测试系统框图Fig.4 Block diagram of the test system used in simulation experiment

图5 模拟实验得到的PIM误差分布Fig.5 Measured distribution of PIM error
2 PIM测试误差讨论
由前述PIM误差分布的分析可知,PIM误差服从一定的统计分布,具有随机性。因此,这里提出采用蒙特卡罗方法模拟研究重复测量法对PIM误差的影响规律。工程实践中,重复测量法有两种实施途径:一是多次测量后取极大值/极小值(在PIM指标要求严格的工程领域中,一般选取最大值,也就是以多次测试值中的最差值来判断产品是否合格),另外一种是多次测量后取平均值。这里将前者称为最大值法,后者称为均值法。
如图6所示为最大值法模拟得到的结果,总共模拟了3种情形,每种情形累计的数据量均为100。以图6(a)为例,“测试次数20”表示最终获得了20个测量结果(每个测量结果对应图中1条短横线),每个测量结果是从连续5次测试读数中选取其中的最大值得到的。这可以类比为某工程师在20个不同时间点利用同一测试系统对同一产品进行了测试,并且每次测试中均读取5次结果,以这5次测试结果的最大值作为最终测试结果。或者也可以看作是20个工程师利用同一测试系统对同一产品进行了测试且每位工程师均测试5次取最大值。如图6(c)所示,当重复测量次数较多时,最大值法测得的PIM值具有更好的一致性或者具有更小的分散性,但是得到的测试结果基本上接近正误差边界,这也意味着最大值法比较保守,大概率会使得PIM测试结果偏大。对于工程实践而言,这相当于预留了指标裕量,但是,从另外一方面来看,这种保守性可能使得原本合格的产品被误判为不合格。

图6 采用蒙特卡罗模拟得到的PIM误差分布(最大值法)Fig.6 Simulated PIM error distribution using Monte Carlo method (maximum method)
如图7所示,给出了均值法模拟得到的结果,总共模拟了两种情形,每种情形累计的数据量均为10000。对比图7(a)所示的平均次数为100的情形和图7(b)所示的平均次数为1000的情形可知,平均次数增多,有利于获得分散性较小的PIM测试结果。需要指出的是,这里的平均次数相对较大,工程实践中若想采用均值法减小PIM测试误差,应当采用自动化测试系统,这样才能在可以接受的测量时长内获得更准确的测试结果。
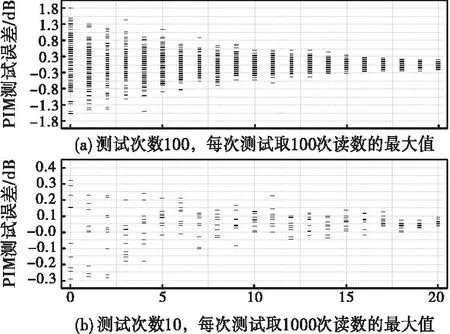
图7 采用蒙特卡罗模拟得到的PIM误差分布(均值法)Fig.7 Simulated PIM error distribution using Monte Carlo method (average method)
在PIM行业内,当需要评估PIM测试误差时,通常依据图1中的上、下边界进行误差评估。例如,当待测互调比系统残余互调高10dB时,图1所示的误差图显示PIM误差的上下边界分别约为+2.4dB、-3.3dB。这意味着如果实测互调电平为-110dBm,则真实互调电平应该位于-112.4dBm至-106.7dBm之间。然而,如果不考虑PIM误差的分布特性,就无法对产品的指标进行更为精细的评估。假设产品合格标准是-110dBm,那前述案例中的测试结果“位于-112.4dBm至-106.7dBm之间”意味着该产品合格的概率是多少?本文的方法及图2中的结果即可对此进行评估。结合目前国内外PIM分析仪产品的指标特性,对PIM测试误差进行更深入的分析,如表1所列。

表1 PIM分析仪技术指标Tab.1 Specification of PIM analyzers
无源互调的测试误差主要来源于馈入待测件的载波功率精度、测试系统残余互调电平、接收机测试精度等系统指标[9]。馈入待测件的载波功率可能由于信号源输出幅度稳定性、功率放大器增益稳定性等因素而存在一定的误差。表1中给出的相关PIM分析仪厂商的产品指标数据显示,标称的载波功率精度典型值在±0.25~0.5dB之间(需注意,同一厂商不同型号产品指标可能略有差异)。实际上,工程实践中可能由于忽略了外接电缆组件产生的损耗而进一步增大载波功率误差。考虑到载波功率每变化1dB,无源器件的互调电平通常会变化2~3dB,载波功率精度是影响PIM测试精度的一个重要因素。
表1还给出了PIM分析仪厂商标称的反射残余互调,分布在-120~-125dBm的范围内,这与移动通信领域常见的PIM指标值(约为-110dBm)相比,低了大约10~15dB,符合IEC标准中的推荐值。假设系统残余互调为-125dBm,并将图1所示的PIM测试误差图的横、纵坐标物理量分别改为真实互调电平、实测互调电平,如图8所示。按照传统的PIM误差分析方法,假如实测PIM电平为-115dBm,由于其比残余互调高10dB,对应的正/负误差为+2.4/-3.3dB,所以真实PIM估计在-117.4~-111.7dBm之间。然而,按照图1中如果实测PIM是-115dBm,其对应的真实PIM范围约为-118~-112.5dBm。造成这种区别的原因在于,图1所示的传统PIM误差图中,其横坐标是真实互调电平与残余互调电平之差,在传统PIM误差分析中,常将实测得到的互调电平作为真实互调电平;而在改进的PIM误差图中,直接使用了实测互调电平,因此从逻辑上更为严谨。当然,改进的PIM误差图与系统残余互调电平相关,这意味着不同的PIM测试系统有不同的误差图。
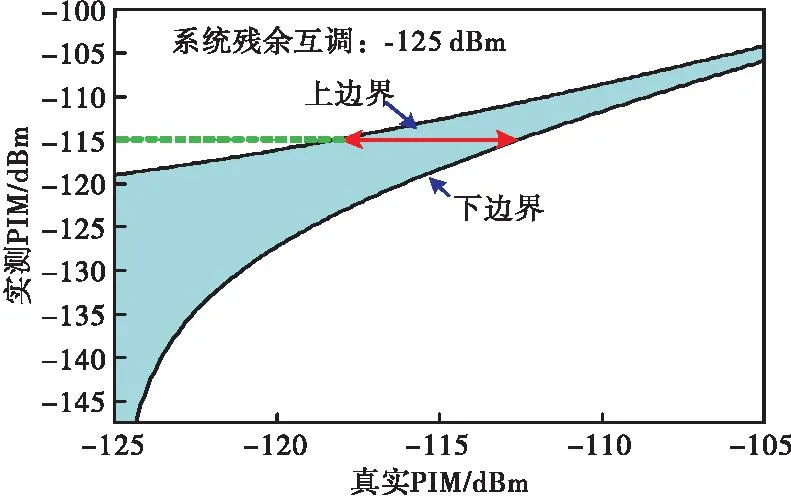
图8 一种改进的PIM误差图Fig.8 An improved PIM error chart
3 结论
基于矢量信号合成理论推导了PIM测试误差与系统残余互调电平的关系,采用蒙特卡罗方法模拟了PIM测试误差的统计分布并进行了初步的实验验证,最终得到了依据实测PIM电平进行PIM测试误差估计的方法。相比于现有PIM测试误差估计方法而言,本文的误差估计方法能同时得到误差边界及其统计分布,可提高PIM测试估计结果的可靠性。需要指出的是,本文假设了残余互调具有单一来源,考虑多个来源的情形是后续研究的重点之一;此外,在实际PIM分析仪上开展本文误差分析理论系统严谨的实验验证也是今后研究的重点。

