基于LADRC算法的柴油发电机组控制研究

雷言开, 张天宏

(南京航空航天大学 能源与动力学院,江苏 南京 210016)

柴油发电机组是一种以柴油为燃料的发电设备,以柴油机为原动机,带动发电机发电。本文研究的对象是基于他励同步发电机的柴油发电机组,目前,这种柴油发电机组是工业供电领域广泛应用的供电设备,常应用于船舶、电站和各种应急供电场合[1]。

本文将柴油发电机组看作以油门开度和励磁电压为输入、转速和端电压为输出的多变量耦合非线性系统,可以通过调整油门开度和励磁电压控制系统的转速和端电压保持稳定,进而实现供电频率和电压的稳定。但柴油机和发电机本身的非线性特性,以及二者间的耦合特性,给稳定控制带来了很大的挑战。因此,为了保证柴油发电机组稳定供电,需要针对用电负载突变工况,研究柴油机与发电机的协同控制方法。

目前,国内外在柴油发电机组控制方面的研究已经发展得较为成熟。柴油发电机组的控制包含两部分:柴油机调速控制和发电机励磁控制。基于比例积分微分(Proportional-Integral-Derivative,PID)的各种改进算法是柴油机常用的调速控制方法。陆平[2]采用动态模式分离PID调节算法和变增益非线性硬件补偿方法来提高系统性能;刘国栋[3]将自适应PID控制理论应用于柴油机调速控制,这种算法具有鲁棒性好、可靠性高等特点。目前,很多学者将神经网络等技术用于柴油机调速控制,如王川川等[4]提出了一种小脑模拟神经网络(Cerbella Model Articalation Controller,CMAC)与PID结合的柴油机调速方案。发电机的励磁控制方法自20世纪50年代以来不断发展。随着现代控制理论的发展,李勇等[5]提出将线性最优控制理论应用到电力系统,有效提高了发电电压的稳定性;Lu等[6]在最优励磁控制的基础上,考虑系统的非线性特性,提出了非线性励磁控制方法,解决了系统非线性干扰问题;励磁控制方法中如今也有许多基于神经网络的智能控制方法[7-8]。

本文针对柴油发电机组负载突变工况,研究柴油机与发电机的协同控制方法。首先,基于柴油机和同步发电机外特性,通过稳态特性插值和动态参数调度的方法建立了柴油发电机组外特性模型,并对模型进行了开环仿真测试,对模型的稳态及动态特性和实时性进行了验证;然后,针对用电负载突变工况,基于线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC)算法,设计了柴油发电机组控制方法,并进行了闭环仿真测试,初步验证算法的控制效果;最后,搭建了硬件在环试验平台,通过硬件在环试验进一步验证算法的控制效果和在柴油发电机组电子控制系统中的工程适用性。

1 柴油发电机组建模

柴油发电机组以柴油机为原动机,带动同步发电机旋转并发电;同步发电机旋转产生的电磁转矩,则作为柴油机的负载。因此,本文将柴油发电机组看作以油门开度、励磁电压为输入,转速和端电压为输出的多变量耦合非线性系统。

本节面向控制研究基于柴油机和同步发电机的外特性,通过稳态特性插值和动态参数调度的方法,分别建立柴油机和同步发电机的外特性模型,最终得到柴油发电机组外特性模型,并对模型进行了开环仿真测试。

1.1 柴油发电机组外特性模型

本节建立的柴油发电机组模型结构示意图如图1所示,油门开度和励磁电压作为模型的输入,转速和端电压作为模型的输出,柴油机和同步发电机之间通过转速和电磁转矩相互耦合,用电负载在同步发电机端作为干扰输入。

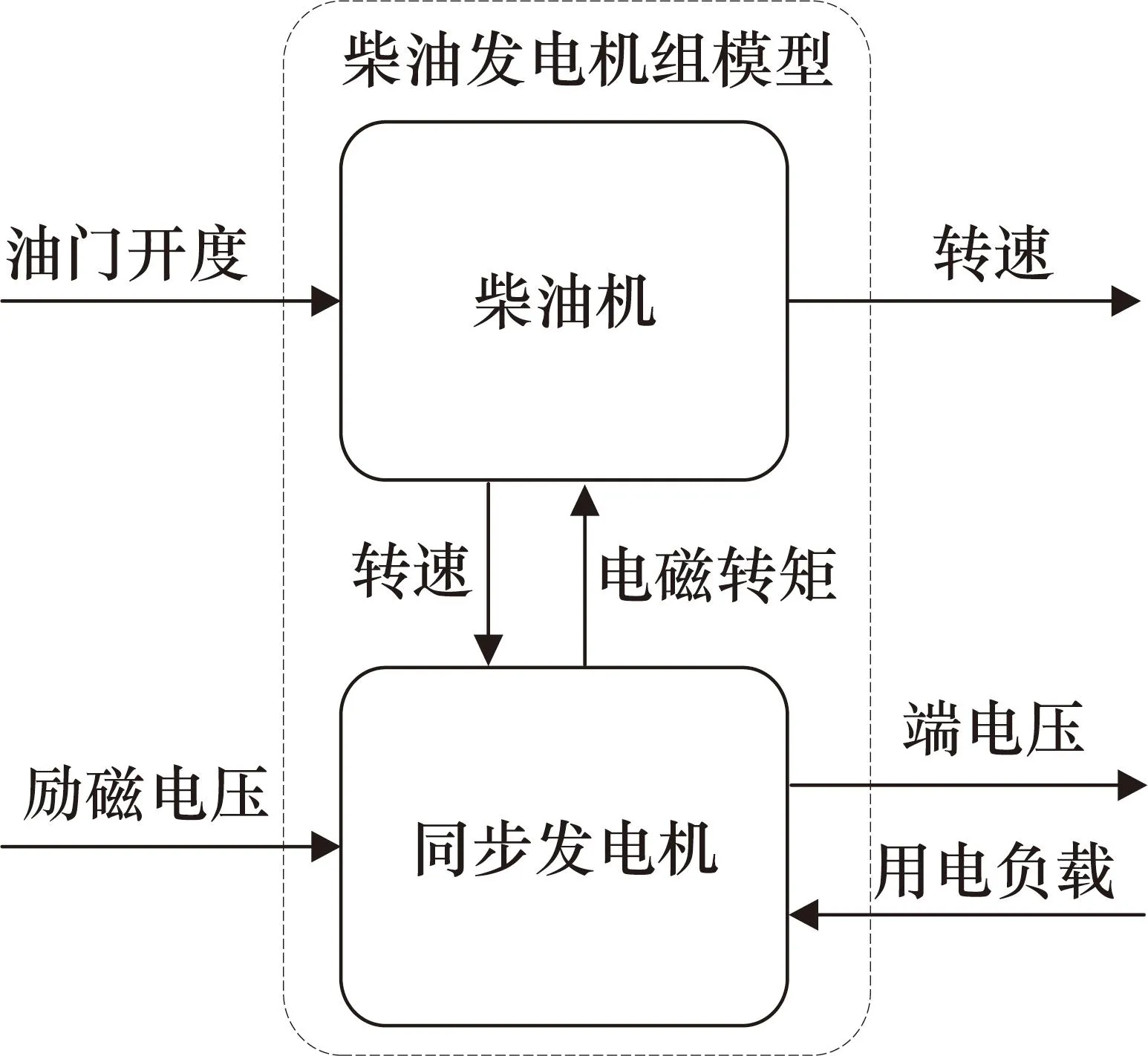
图1 柴油发电机组模型结构示意图

柴油发电机组模型技术参数如表1所示。

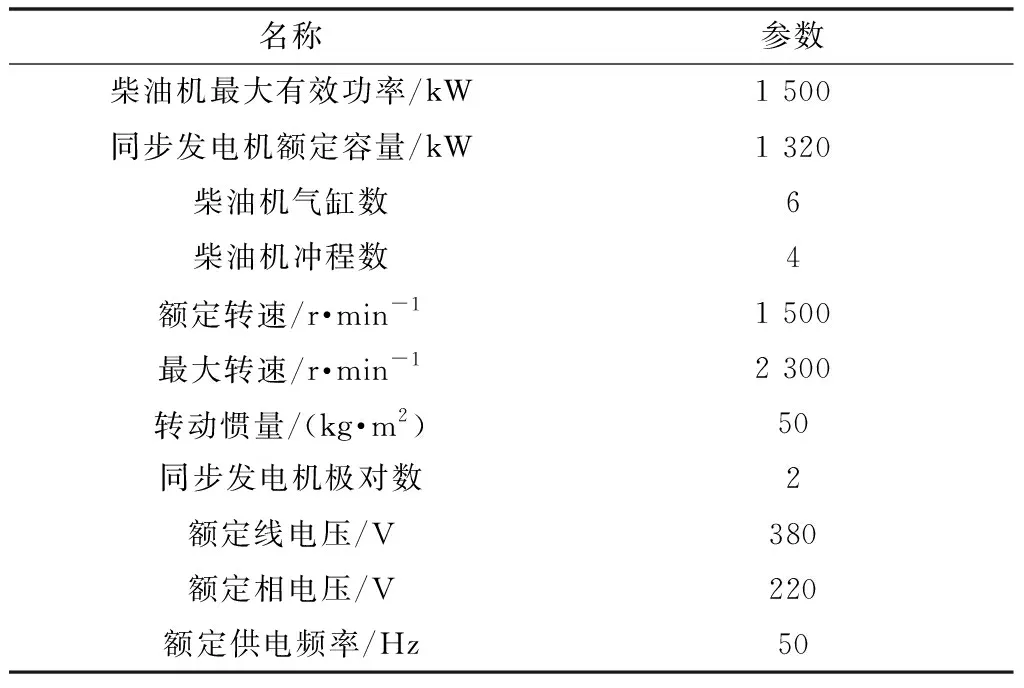
表1 柴油发电机组模型技术参数

1.1.1 柴油机外特性模型

柴油机的速度特性是指:油门位置不变时,柴油机性能指标随转速ng的变化关系。这些性能指标包括:有效功率Pe,输出转矩Ttq,燃油消耗率be等[9]。柴油机的外特性是指:油门位置固定在标定功率循环供油量的位置时,测得的速度曲线。

本文建立的柴油机外特性模型如式(1)～式(3)所示,这些表达式反映了柴油机模型的油门开度、有效功率、输出转矩和柴油机转速的关系。

Pe=α·Pmax·p(ω)

(1)

(2)

p(ω)=0.652 6ω+1.694 8ω2-1.347 4ω3

(3)

式中:α为油门开度;Pmax为最大有效功率;ng为柴油机转速;p(ω)为功率需求函数;ω为转速比(柴油机转速与额定转速之比)。

柴油机的外特性反映了柴油机的稳态特性,而柴油机作为一个复杂的非线性系统,影响其动态特性的因素有很多。本文只考虑柴油机转子旋转运动时的动力学特性,以及柴油机内部能量传递时,由燃料喷射入气缸到燃烧做功并通过曲轴输出的延迟。

在研究柴油机转子动力学特性时,将柴油机和其带动的负载看作两个联轴的旋转质量体,可以得到柴油机的动力学方程:

(4)

式中:TL为负载转矩;Je为柴油机转动惯量;JL为负载转动惯量。

柴油机做功时,燃料喷射入气缸到燃烧做功并通过曲轴输出,这个过程需要经历一段延时,也称为IPS-Delay(Introduce to Power Stroke-Delay),延迟τe计算如式(5)所示,本文在建模时将其看作纯延迟环节。

(5)

式中:C为延时系数;Nst为冲程数;Ncyl为气缸数。

基于上述柴油机稳态和动态特性计算方法,搭建了柴油机外特性模型,模型计算示意图如图2所示。

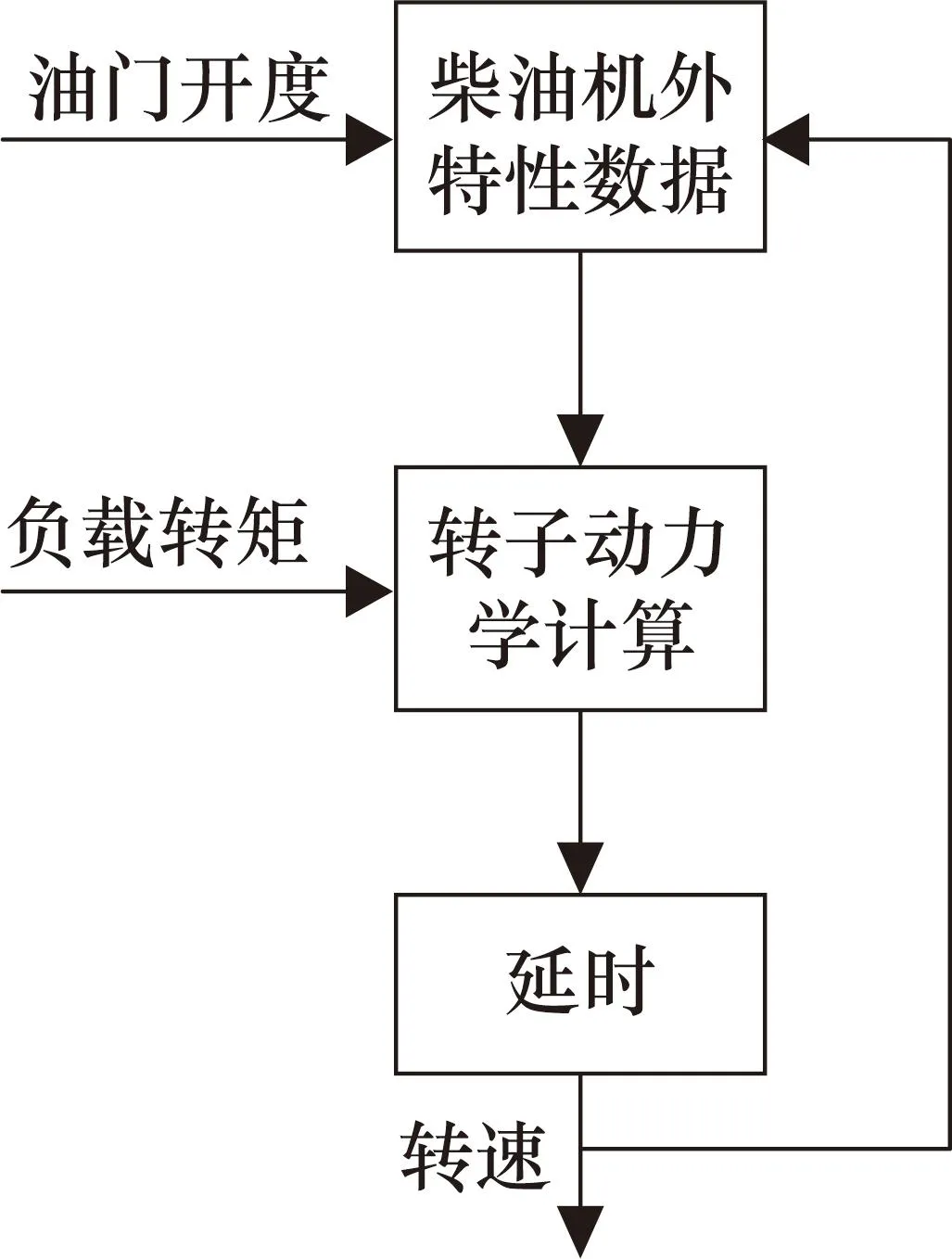
图2 柴油机模型计算示意图

当负载转矩发生变化时,模型的计算过程为:首先,基于柴油机外特性,根据油门开度,通过式(1)～式(3)可以得到输出转矩;然后,通过式(4)即转子动力学方程计算输出转矩和负载转矩的平衡过程,得到输出转速的变化;最后,考虑式(5)所示的时滞特性,得到最终的输出转速。

按上述方式计算,直至柴油机输出转矩与负载转矩平衡。

1.1.2 同步发电机外特性模型

如图3所示,本文将同步发电机看作以转速、励磁电压、用电负载为输入,端电压、端电流、电磁转矩为输出的系统。基于同步发电机在全工作范围内各输入与各输出之间的稳态和动态特性,即同步发电机外特性,建立了同步发电机外特性模型。

图3 同步发电机模型结构示意图

通过对同步发电机进行辨识,得到了外特性参数。其中稳态特性参数反映了同步发电机在不同工作点的输入与输出的稳态对应关系。在建立同步发电机模型时,选择的稳态工作点范围是:转速1 000～2 200 r/min,励磁电压0.5～3.5 pu(标幺值),用电负载132～1 320 kW。在各稳态工作点,分别对同步发电机3个输入施加小幅阶跃,通过3个输出的阶跃响应可以得到在不同的工作点同步发电机的动态特性参数(如增益和时间常数)。

设同步发电机外特性模型的输入分别为:转速ne,励磁电压Vf,用电负载RL;输出分别为端电压U,端电流I,电磁转矩T;各工作点的动态特性参数分别为K1,K2,…,Kn(动态特性参数由对具体工作点进行辨识得到,不同工作点参数个数不同)。同步发电机外特性模型的计算方式如式(6)所示:

(6)

式中:f1、f2、f3分别为计算端电压、端电流和电磁转矩的一系列插值函数。通过这种计算方式,模型可以表示同步发电机在不同工作点的稳态和动态特性。

1.2 柴油发电机组模型仿真分析

在1.1节中建立了柴油发电机组外特性模型,为了对模型进行验证,选择60%(792 kW)用电负载工况,分别对励磁电压和油门开度施加阶跃,并得到相对应的转速、端电压、端电流以及电磁转矩阶跃响应。

1.2.1 励磁电压开环阶跃测试

在60%用电负载工况下,保持油门开度不变,从额定状态,即转速1 500 r/min,端电压220 V,对励磁电压施加连续阶跃。设初始油门开度为0.531 9,初始励磁电压为1.929 pu ,励磁电压在5 s时开始向下阶跃至1.5,此后每10 s向下阶跃0.5,直至励磁电压为1 pu。柴油发电机组转速、端电压、端电流和电磁转矩的响应如图4所示。

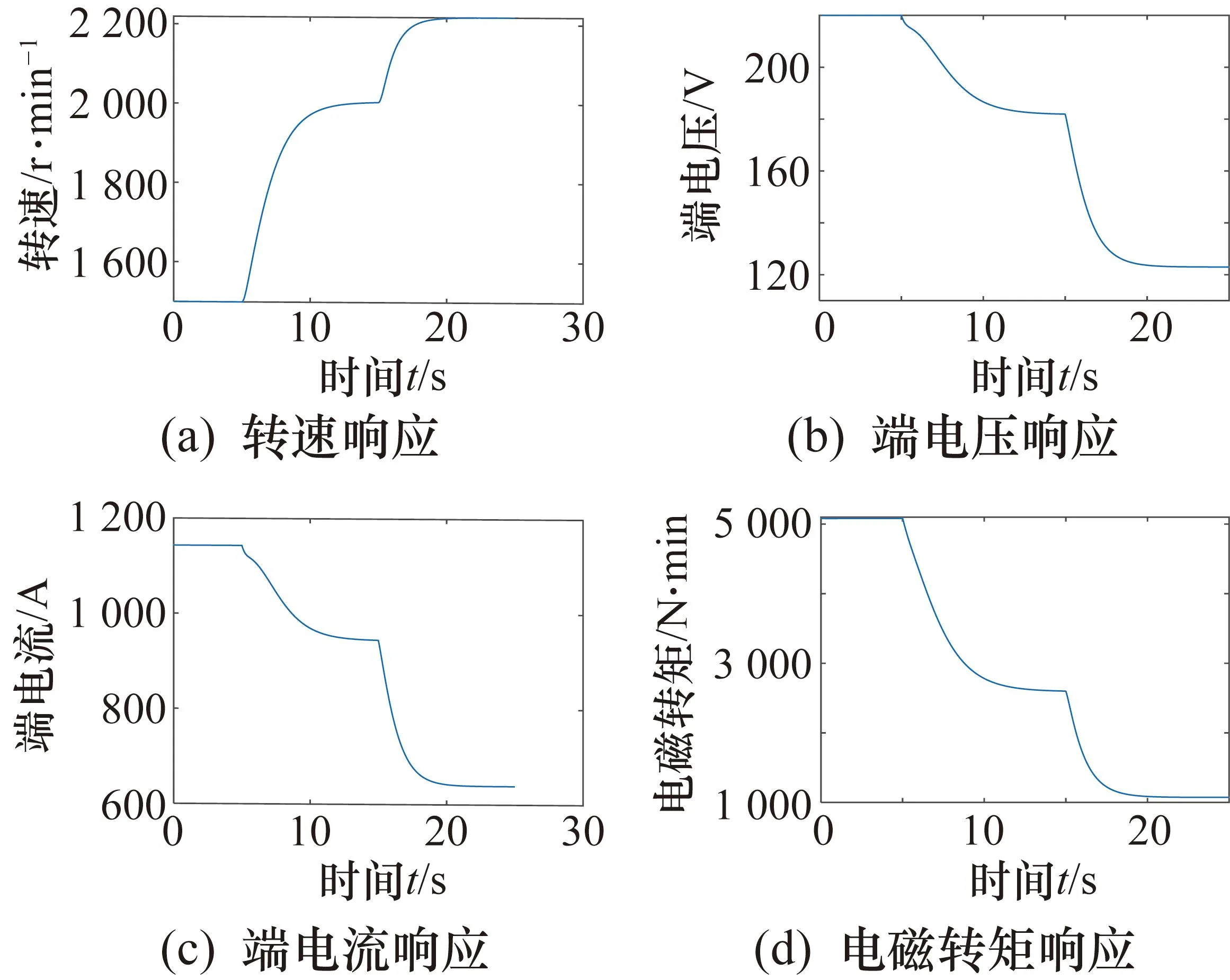
图4 60%负载工况下励磁电压连续阶跃响应

由图4可知,当油门开度和用电负载不变时,随着励磁电压的逐渐减小,柴油发电机组模型输出的端电压、端电流逐渐减小,同步发电机产生的电磁转矩逐渐减小,系统转速逐渐增大。对于柴油发电机组而言,励磁电压减小会使同步发电机内部磁场强度减小,因此端电压、端电流和电磁转矩会减小;在油门开度不变的情况下,电磁转矩减小会使系统转速增大。因此模型的励磁电压阶跃响应与柴油发电机组实际特性相符。

1.2.2 油门开度开环阶跃测试

在60%用电负载工况下,保持励磁电压不变,从额定状态,即转速1 500 r/min,端电压220 V,对油门开度施加连续阶跃。设初始油门开度0.531 9,励磁电压1.929 pu,油门开度在5 s时阶跃至0.6,在25 s时阶跃至0.7。转速、端电压、端电流和电磁转矩阶跃响应如图5所示。

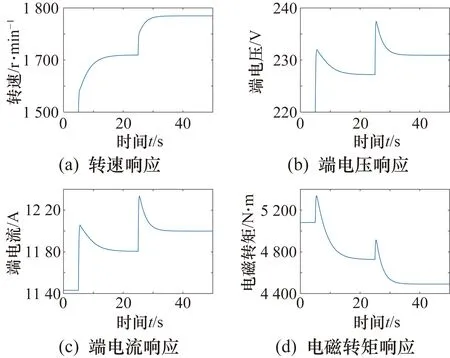
图5 60%负载工况下油门开度连续阶跃响应

由图5可知,当励磁电压和用电负载不变时,随油门开度逐渐增大,系统转速逐渐增大,柴油发电机组模型输出的端电压、端电流逐渐增大,同步发电机产生的电磁转矩逐渐减小。对于柴油机发电机组而言,当油门开度增大时,输出的转速、端电压、端电流会增大。由于用电负载是保持不变的,因此同步发电机输出端消耗的功率也不变。因此,从功率平衡的角度看,柴油发电机组转速增大,同步发电机产生的电磁转矩必然会减小。因此,模型的油门开度阶跃响应与柴油发电机组实际特性相符。

2 柴油发电机组控制算法设计

自抗扰控制算法将所有作用于控制对象的未知因素定义为“扰动”,通过引入扩张观测器(Extended State Observer,ESO),不需要精确的数学模型便可以估计系统的总扰动,并进行补偿[10]。Gao[11]提出了LADRC算法,通过调整观测器带宽和控制器带宽进行LADRC算法参数优化与整定的方法,使LADRC算法更便于工程实践应用。

柴油发电机组以油门开度和励磁电压为输入,转速和端电压为输出,用电负载作为发电机端的干扰输入。柴油机和同步发电机之间通过转速和电磁转矩紧密耦合,这种耦合特性给柴油发电机组的控制带来了挑战。因此,基于LADRC算法的原理和特点,将柴油发电机组耦合特性对控制系统的影响看作“扰动”,设计ESO进行观测并补偿,可以有效解决柴油机和同步发电机协同控制的耦合问题。

本节基于柴油发电机组模型,针对柴油发电机组用电负载突变工况,分别采用LADRC算法和比例积分(Proportional-Integral,PI)控制算法设计控制器,并进行仿真对比二者控制效果。

2.1 柴油发电机组LADRC控制器设计

图6为柴油发电机组控制系统示意图。将用电负载的变化以及柴油机和同步发电机之间耦合特性的影响看作是系统的“扰动”。将柴油机看作一阶系统,设计扩张观测器ESO1观测系统的转速Ne和对柴油机的扰动fe;将同步发电机也看作一阶系统,设计扩张观测器ESO2观测系统的端电压U和对同步发电机的扰动fg。基于ESO的反馈,控制器根据参考转速Nref和参考端电压Uref控制油门开度α和励磁电压Vf,保证柴油发电机组的转速和端电压稳定。

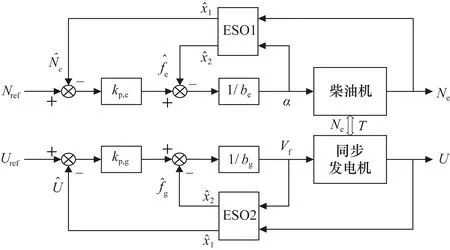
图6 柴油发电机组LADRC控制系统示意图

柴油发电机组控制系统的关键是ESO的设计,本文分别设计了柴油机扩张观测器ESO1和同步发电机扩张观测器ESO2,并设计了油门开度和励磁电压的控制方法。

(1) 柴油机扩张观测器ESO1设计。

柴油机扩张观测器ESO1的方程为

(7)

对ESO1的极点进行配置,如式(8)所示,应将极点配置在-ω0(ω0>0)处,由文献[12]可知,这样对于干扰的敏感性最低。

(8)

此时油门开度控制信号为

(9)

柴油机转速控制系统闭环传递函数为

(10)

令柴油机控制器增益kp,e=ωc=20,柴油机扩张观测器带宽ω0=70,be=912。

(2) 同步发电机扩张观测器ESO2设计。

同步发电机扩张观测器ESO2的方程为

(11)

ESO2的极点配置与ESO1相同,令β1=2ω0,β2=ω0,bg=148。此时励磁电压控制信号为

(12)

同步发电机端电压控制系统闭环传递函数为

(13)

令控制器增益kp,g=ωc=50,扩张观测器带宽ω0=10。

2.2 柴油发电机组控制算法仿真分析

2.2.1 LADRC算法仿真分析

本节基于LADRC算法搭建了如图6所示的柴油发电机组控制仿真系统,LADRC控制器的参数设置如2.1节所述。设参考转速1 500 r/min,端电压220 V。分别针对用电负载小幅突变和大幅突变工况进行仿真。

(1) 用电负载小幅阶跃测试。

设柴油发电机组的初始状态为额定状态,即转速1 500 r/min,端电压220 V。初始用电负载为50%(660 kW),每次阶跃的幅度为10%(132 kW),在柴油发电机组正常工作范围内分别测试了用电负载向上阶跃和向下阶跃,仿真测试结果如图7所示。

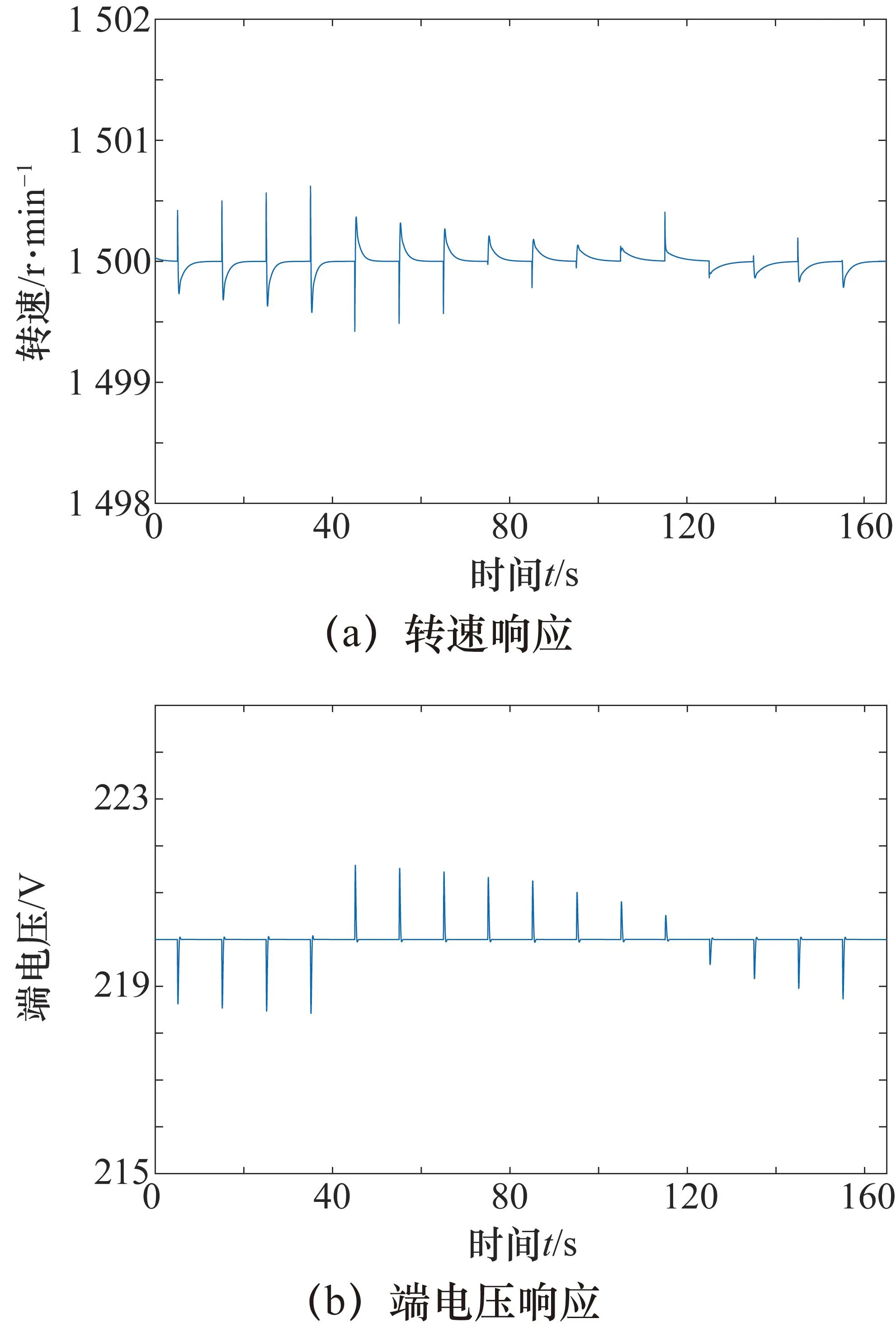
图7 用电负载小幅阶跃时LADRC控制仿真结果

由图7可见,用电负载小幅突变时,转速波动小于0.1%,端电压波动小于0.6%。

(2) 用电负载大幅阶跃测试。

设柴油发电机组的初始状态为额定状态,即转速1 500 r/min,端电压220 V。初始用电负载为50%(660 kW),每次阶跃的幅度为40%(528 kW),在柴油发电机组正常工作范围内分别测试了用电负载向上阶跃和向下阶跃,仿真测试结果如图8所示。

由图8可见,用电负载大幅突变时,转速波动小于0.2%,端电压波动小于2.5%。

2.2.2 PI算法仿真分析

如图9所示,本节搭建了柴油发电机组PI控制仿真系统,设柴油机PI控制器参数为:比例增益Kp,g=0.015,积分增益Ki,g=0.02;设同步发电机PI控制器参数为:比例增益Kp,e=0.1,积分增益Ki,e=0.05。设参考转速1 500 r/min,端电压220 V。分别针对用电负载小幅突变和大幅突变工况进行数字仿真。

图9 柴油发电机组PI控制系统示意图

(1) 用电负载小幅阶跃测试。

设柴油发电机组的初始状态为额定状态,即转速1 500 r/min,端电压220 V。初始用电负载为50%(660 kW),每次阶跃的幅度为10%(132 kW),在柴油发电机组正常工作范围内分别测试了用电负载向上阶跃和向下阶跃,仿真测试结果如图10所示。

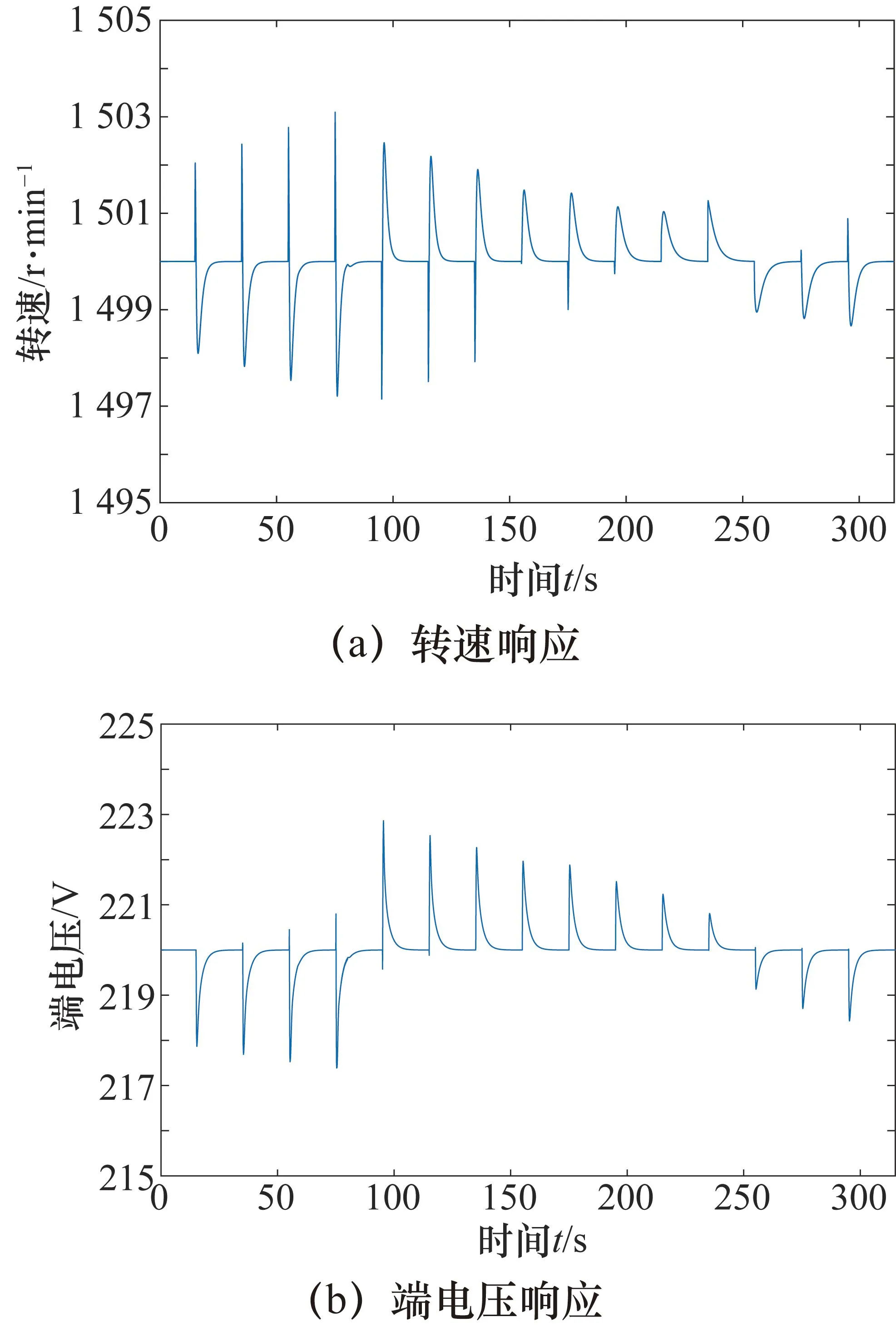
图10 用电负载小幅阶跃时PI控制仿真结果

由图10可以看出,用电负载小幅突变时,转速波动小于0.3%,端电压波动小于1.0%。

(2) 用电负载大幅度阶跃测试。

设柴油发电机组的初始状态为额定状态,即转速1 500 r/min,端电压220 V。初始用电负载为50%(660 kW),每次阶跃的幅度为40%(528 kW),在柴油发电机组正常工作范围内分别测试了用电负载向上阶跃和向下阶跃,仿真测试结果如图11所示。

图11 用电负载大幅阶跃时PI控制仿真结果

由图11可见,用电负载大幅度突变时,转速波动小于0.8%,端电压波动小于4.0%。

表2为PI控制和LADRC控制效果对比。

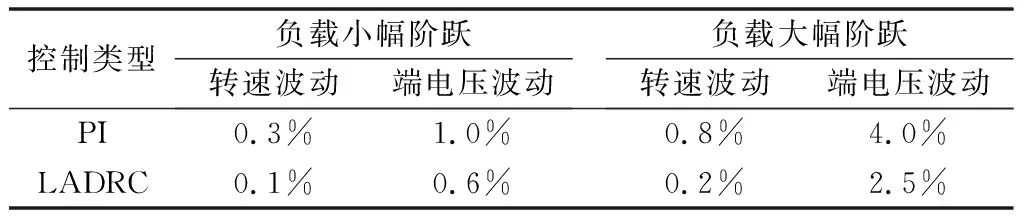
表2 PI与LADRC控制效果对比

同样的用电负载变化工况下,在LADRC控制算法的调节下,柴油发电机组转速和端电压的波动更小,因此,LADRC算法的控制效果优于PI控制,对不同工况的适应性更好。

3 硬件在环试验验证

为了进一步验证LADRC算法的控制效果和在柴油发电机组电子控制系统中的工程适用性,搭建了硬件在环试验平台,针对用电负载突变工况,进行了硬件在环试验验证。

3.1 硬件在环试验平台简介

基于MT RobustRIO实时控制系统搭建了硬件在环试验平台。采用的柴油发电机组电子控制器可以采集端电压、端电流、油门位置和缸盖温度等传感器信号。假设柴油发电机组油门调节机构为步进电机,电子控制器可以输出步进电机控制信号和励磁控制信号。

如图12所示,本节搭建的硬件在环试验平台分为两部分,分别是柴油发电机组仿真接口模拟器和电子控制器。电子控制器采集仿真接口模拟器模拟的端电压、端电流、油门开度、缸盖温度和转速等传感器信号,根据控制算法计算出控制量,输出步进电机方向控制信号、步进电机步数控制信号和励磁电压控制信号;仿真接口模拟器内运行柴油发电机组模型,通过AI、DI输入采集端口接收电子控制器的指令,换算为对应的油门开度和励磁电压,柴油发电机组模型模拟计算出端电压、转速等运行状态,然后通过AO、DO等输出端口传送给电子控制器。

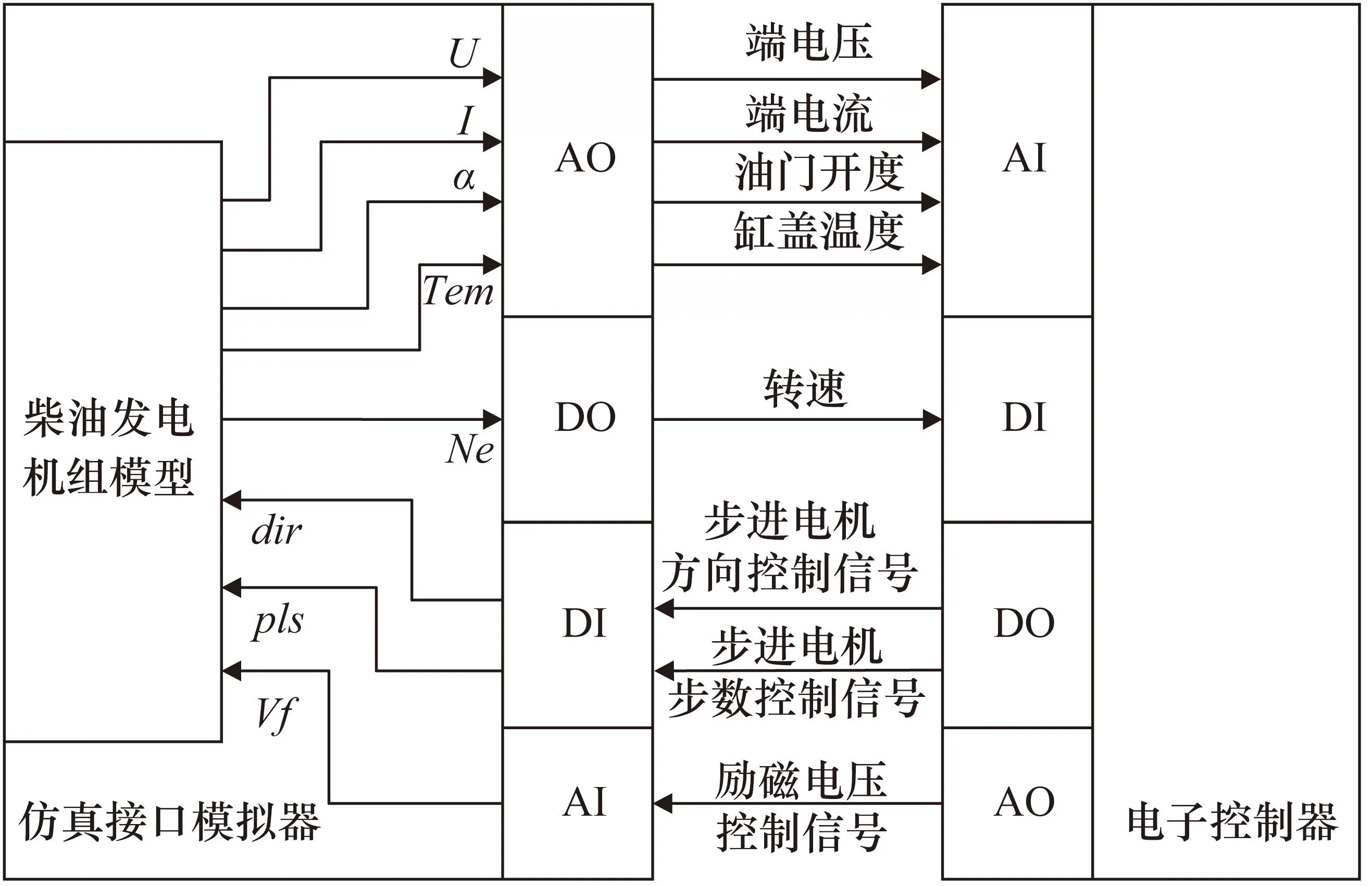
图12 硬件在环试验系统

图13为柴油发电机组硬件在环试验系统实物图。

图13 硬件在环仿真试验系统实物图

3.2 硬件在环仿真试验

本节进行了硬件在环试验验证。分别在不同工作点进行用电负载小幅突变(132 kW/次)和大幅突变(528 kW/次)两种工况测试,进一步验证LADRC算法控制柴油发电机组转速和端电压保持稳定的效果,仿真结果如图14和图15所示。

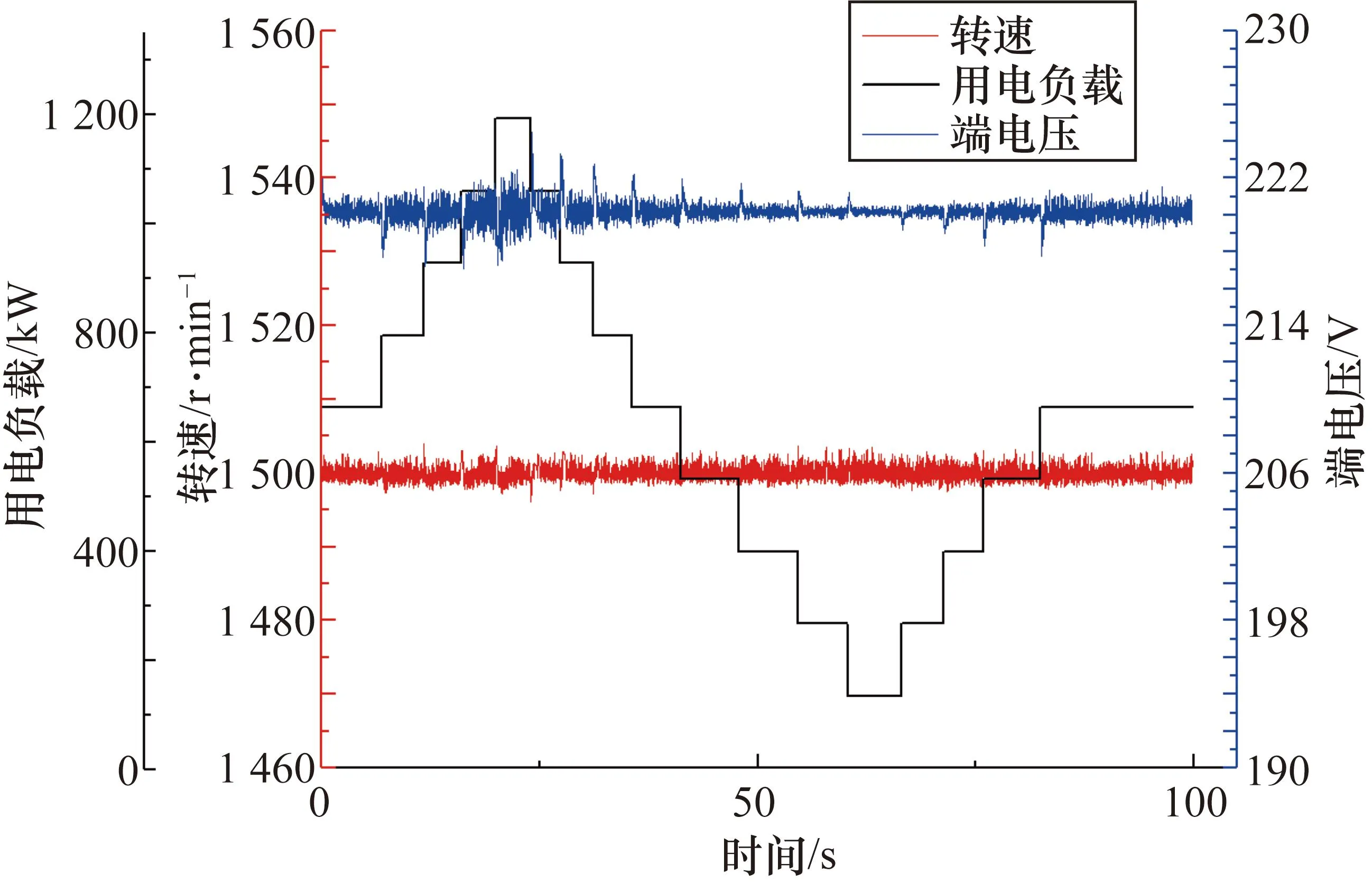
图14 用电负载小幅突变硬件在环试验结果

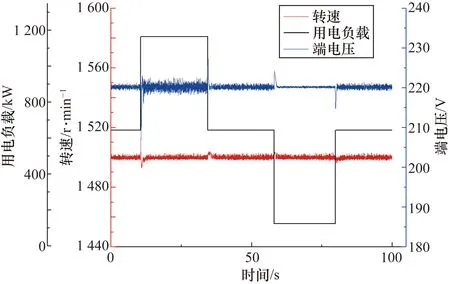
图15 用电负载大幅突变硬件在环试验结果

由图14和图15可见,用电负载小幅突变时柴油发电机组转速波动小于4 r/min(0.27%),端电压波动小于5 V(2.3%);用电负载大幅突变时柴油发电机组转速波动小于12 r/min(0.8%),端电压波动小于12 V(5.5%)。

根据国家发布的《电能质量供电电压偏差》和《电能质量供电频率偏差》:20 kV及以下三相供电电压偏差不超过为标称电压的±7%;电网容量在3×106kW以下,供电频率偏差不超过±0.5 Hz。硬件在环试验结果表明,通过LADRC算法可以在不同用电负载突变工况下控制柴油发电机组端电压波动小于5.5%,转速波动小于0.8%(供电频率波动小于0.4 Hz),能满足国家供电标准。因此,实现了保持柴油发电机组发电电压和频率稳定的控制目标。

4 结束语

本文以基于他励同步发电机的柴油发电机组为研究对象,针对用电负载突变工况,研究柴油机与同步发电机的协同控制方法,实现了保证柴油发电机组供电电压与频率稳定的目标。

① 本文面向柴油发电机组控制研究,基于柴油机和同步发电机的外特性,通过稳态特性插值和动态参数调度的方法建立了柴油发电机组外特性模型,并对模型进行了开环数字仿真,结果表明建立的外特性模型可以反映柴油发电机组稳态和动态特性,以及系统非线性耦合特性,适用于柴油发电机组控制研究。

② 针对用电负载突变工况,分别基于PI控制算法和LADRC算法设计了柴油发电机组控制方法,并分别进行了用电负载小幅突变和大幅突变工况下的闭环数字仿真,结果表明LADRC算法控制效果更好,可以控制柴油发电机组供电电压并保持频率稳定。

③ 搭建硬件在环试验平台,进行硬件在环试验,进一步验证了用电负载突变时,LADRC算法的控制效果和实际柴油发电机组电子控制系统的适用性。试验结果表明,柴油发电机组供电频率波动小于0.4 Hz,端电压波动小于5.5%,满足国家供电标准,实现了控制柴油发电机组发电电压和频率稳定的目标。