某压气站管道减振措施研究
刘恩斌 ,廉殿鹏,2,王兴杰,3,苏中亚,谢 萍
1.西南石油大学石油与天然气工程学院,四川 成都 610500;2.中联煤层气有限责任公司晋西分公司,山西 吕梁 033200;3.中国石化江汉油田石油工程技术研究院,湖北 武汉 430030;4.中国石化中原石油工程设计有限公司,河南 郑州 450006;5.国家管网西部管道公司,新疆 乌鲁木齐 830000
引言
管道振动严重威胁管道安全[1-3]。在天然气管道压缩机站中,由于压力、流量波动及压缩机设备的不平稳运行造成气流脉动等原因都会引起站场管道出现振动[4-5]。轻微振动是可以通过支架和阻尼装置等处理,不会对管道系统造成破坏,但持续强烈的振动会在管道与附件的连接部位和管道与支架的连接部位等产生较大的交变应力,导致整个管道系统疲劳失效,造成焊缝开裂、螺栓松动、仪表损坏和介质外泄等,若泄漏的是易燃易爆气体,则会对输气管道的安全生产、经济运行及环境等构成巨大威胁[6-7]。因此,应该对管道进行振动治理,找到管道振动原因并制定减振措施,以实现管道系统平稳运行。
输气管道的流致振动是一种常见的流固耦合振动现象,一方面,管道与其相连接的阀门、容器及各类支固架等共同构成一个机械结构系统;另一方面,管道中输送的流体在弯头、三通等处产生方向、大小各不相同的激振力。这些大小不同、相位各异的激振力作用在管道上,使管道产生振动响应[8-10]。Tian 等[11]运用传递矩阵法发现,当压力脉动频率接近气柱基频和固有频率的整数倍时,振动强度会增强。Li等[12]以输液管道为研究对象,发现支座位置和刚度变化对低弯矩模态和高扭转模态的影响最大。Khudayarov 等[13]运用有限元方法发现如果在充满瞬变流体的充液管道分析中考虑流体-结构相互作用(FSI),则结构速度会大大降低。管路系统的FSI 能够改变其振动响应及固有特性,流体压力波的阻尼更强,并且管路系统柔性越大,管道流固耦合作用会增强。目前,利用流固耦合方法研究管道流致振动的方法越来越成熟,且在大型天然气站场管道分析中得以运用。本文针对某天然气站场出站管道的振动问题,采用流固耦合方法来进行研究,找到管道振动原因并给予合理建议。
1 模型建立
在流体动力学理论基础上,构建了如下的数学模型。
1.1 固体轴向运动模型
管道轴向运动的控制方程[14]描述了结构的行为,其表达式为
式中:uz—管道轴线方向位移,m;
t—时间,s;
ct—轴向应力波速,m/s;
z—轴向方向,无因次;
v—泊松比,无因次;
g-重力加速度,g=9.8 m/s2;
ρf—流体密度,kg/m3;
R-管道内径,m;
ρt—管材密度,kg/m3;
e-管道壁厚,m;
H-流体压头,m;
Af—流体横向面积,m2;
At—管壁截面积,m2;
f—摩擦系数,无因次;
Vr—流体相对速度,m/s;
γ-管道仰角,(°)。
1.2 流体控制方程
20 世纪50 年代,经典水锤理论进一步发展,形成扩展水锤理论。在该理论中,流动被认为是一维等温流动,动量方程和连续性方程使用平均流速表达。方程可以描述为
式中:
V—管道系统中的流体速度,m/s;
E—管材的杨氏模量,Pa;
σz—轴向应力,Pa;
Kf—流体体积弹性模量,Pa。
1.3 几何模型及边界条件
为建立符合现场实际情况的分析模型,在管道轴测图、竣工安装图、工艺流程图、工艺管网安装图及清管区安装详图等图纸的基础上,通过现场调研,搜集实际的运行参数。如图1 所示,确定了压气站管道振动的主要区域,即三线发球筒管线,特别是发球筒管线盲板处及盲板附近的平衡管线处,从而建立了如图2 所示的计算模型。

图1 发球筒管线现场图Fig.1 Field drawing of launcher pipeline

图2 发球筒管线计算模型Fig.2 Calculation model of launcher pipeline
压气站发球筒管线共涉及4 种不同管径壁厚的管道,管材的密度为7 850 kg/m3,弹性模量为2.06×1011Pa,泊松比均为0.3。由于计算涉及到流体与固体结构之间的相互耦合,需要对发球筒管线和管内填充流体分别进行网格划分。固体部分网格划分共生成1 956 175 个节点,929 890 个单元;流体部分网格划分共生成600 251 个节点,1 778 949 个单元,网格质量均大于0.35,疏密度良好,能够很好地满足后续计算要求。在流固耦合分析中,边界条件设置如图2 所示,入口为速度进口,出口为压力出口,其他出口设置为无滑移壁面。
流固耦合计算模型的固体部分及流体部分的网格划分结果如图3,图4 所示。

图3 固体部分网格划分Fig.3 Meshing diagram of solid part

图4 流体部分网格划分Fig.4 Meshing diagram of fluid part
2 结果与讨论
2.1 模型验证
为验证流固耦合模型是否符合实际情况,使流固耦合分析结果更加可信。现场测试监测点位置如图5 所示。

图5 发球筒管线现场测试点分布图Fig.5 Distribution of field test points of launcher pipeline
在建立的模型中选取同样的监测位置,如图6所示,以流量进口1 流量5 000×104Nm3/d,流量进口2 流量4 000×104Nm3/d 为例,将数值模拟结果与现场测试结果对比,如图7 所示,其最大误差在15%以内,验证了数值分析模型的正确性。

图6 流固耦合振动分析各监测点示意图Fig.6 Schematic diagram of monitoring points for fluid structure coupling vibration analysis

图7 数值计算结果与现场实际测量结果比较Fig.7 Comparison between numerical calculation results and field actual measurement results
2.2 模态分析
Ansys WorkBench 中的模态分析通常不考虑阻尼影响,利用其中的Modal 功能可进行模态分析[15]。将模型导入并设置相关材料属性,其中,管材密度为7 850 kg/m3,弹性模量为2.06×1011Pa,泊松比为0.3,同时设置模态分析阶数为20 阶,经计算得到压气站发球筒管线的前20 阶固有频率如图8所示。
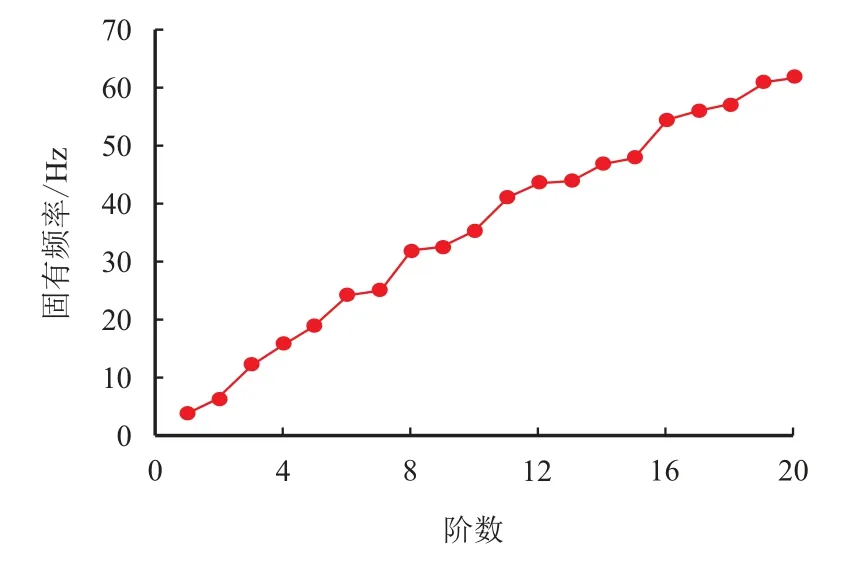
图8 振动管段固有频率Fig.8 Natural frequencies of vibration pipe section
2.3 多工况流固耦合分析
对管道进行多工况流固耦合分析,从而判断管道是否出现共振现象。
在进行流固耦合分析时,设计了3 种极端工况,第一种工况为按照压气站的设计输量,将8 600×104Nm3/d 的流量全部由联通管线流入三线,由此来分析管道内流体压力波动及各监测点的振动情况;第二种工况为联通管线内不通过流量,8 600×104Nm3/d 气体全部由三线压缩机出口汇管而来;第三种工况为联通管线和三线压缩机出口汇管都通过8 600×104Nm3/d 的气体。通过3 种工况之间的交叉比较,可以发现联通管线对管道振动的影响,找到管道振动原因。
根据气体流经的管道管径不同,将流量等效换算成气体流速,定义为不同的速度入口。3 种工况条件如表1 所示。

表1 流固耦合分析各工况表Tab.1 Working conditions of fluid structure coupling analysis
模拟的时间总长为1.2 s,以t=1.2 s 时刻为例,管内流体压力等值线图及流线图如图9 所示。

图9 流体压力等值线图及流线图Fig.9 Fluid pressure contour and streamline
通过图9 可以看出,压气站发球筒管线压力较低,压力较高部分为二线与三线的联通管线和三线出站管线,出站部分的管内压力过渡平缓,但在弯头和三通区域,压力会出现明显变化,即在这些区域管道内形成了明显的涡流区。与工况一及工况二相比,工况三管内流体流速有了明显提高,其最高流速达到了54.9 m/s。
通过米塞斯应力分布并在CFD-Post 后处理中,利用inset-location-volume 操作显示三线发球筒管线流体部分涡核区。为监测管内涡核区域的压力波动,在涡流核心区域设置监测点,监测点位置如图10 所示。

图10 监测点设置Fig.10 Setting of monitoring points
经过模拟,得到各监测点压力-时间数值,对其进行FFT 变换,得到管道涡流核心区域压力波动频谱图,如图11 所示。

图11 各工况频谱图Fig.11 Spectrum of each working condition
通过图11 可以看出,3 种工况下,压气站发球筒管线涡流核心区域压力波动频率主要集中在低频范围0~7.500 Hz。工况二与工况一相比,其在低频范围内的压力脉动幅值明显减小。通过模态分析可知,压气站发球筒管线的前两阶固有频率分别为:一阶固有频率3.953 Hz,二阶固有频率6.292 Hz。管道内压力波动频率与管道系统的低阶固有频率相近,因此,整个压气站发球筒管道系统存在共振现象。
在3 种工况下,V1~V6 振动监测点3 个方向的最大振动速度如图12 所示。

图12 最大振动位移和速度Fig.12 Maximum vibration displacement and velocity
从振动方向来说,主要表现为Y向,即管道的水平方向振动较严重。3 种工况下,发现振动速度较大的监测点为1#、2# 和5#,5# 振动最为剧烈,振动位移和速度都最大,振动现象主要集中在发球筒盲板及盲板附近的平衡管线,与站场管道的实际情况相符。工况三最大振动速度达到117.29 mm/s,按照《压缩机管道振动控制标准》,取允许速度峰值为70 mm/s,最大的振动速度峰值远超70.00 mm/s。通过3 种极端工况分析,无论采用哪种调度方式,管道均会出现剧烈振动,若要避免振动,管道流量应控制在5 000×104Nm3/d。显然,不能满足管道正常运行要求,因此,需要对管道采取一系列减振措施。
通过对模型计算结果进行系统分析,找到管道振动较为严重位置,分析振动现象发生原因,进而采取有效措施对管道振动进行治理,解决工程现场实际问题。
2.4 管道减振措施研究
振动治理主要从两方面入手,即增加管道支撑和改变配管方案。通过设置锚固墩和管夹约束,提高管道系统刚度,使其能够抵抗流体激振力;通过增大联通管线管径,改变流体的流动状态,减小流体激振力[16]。由此提出两种减振方案,具体方案如下。方案一:新增5 处约束,即图13 中的M1-M5。
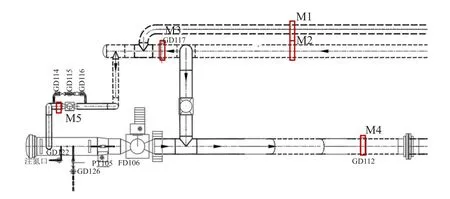
图13 新增约束图Fig.13 New constraint diagram
其中,M1M4 为新增加的管道埋地处的锚固墩约束,M3、M4 为将管道原来的支撑GD112 和GD117 改变为锚固墩约束,其作用位置不变,M5 为新增加的发球筒平衡管线上的管夹约束。
方案二:将原ϕ711 mm×22.2 mm 的联通管线改为ϕ1 016 mm×26.2 mm,同时按方案一增加固定约束,如图14 所示。

图14 改管示意图Fig.14 Schematic diagram of pipe changing
运用上述方法,对改管方案中的发球筒管线进行模态分析,其结果图15 所示。
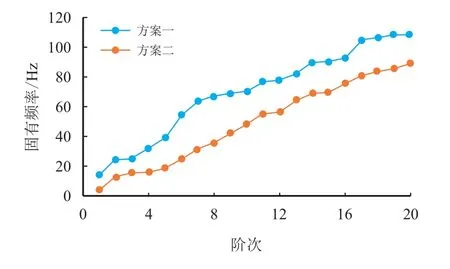
图15 整改后发球筒管线固有频率Fig.15 Natural frequency of launcher pipeline after rectification
从模态分析结果可以看出,在管道上增加锚固墩及管夹约束,管道的刚度提高,因此,整个压气站发球筒管道系统的固有频率提高。以工况三(速度进口1:25.4 m/s,速度进口2:12.0 m/s,压力出口:11.2 MPa)为例,对整改后的发球筒管线进行流固耦合分析,同时,对各压力波动数值进行FFT 变换,得到改管后的涡流核心区域压力波动频谱图,如图16所示。同时,得到整改后1#-6#振动监测点3 个方向的最大振动速度,如图17 所示。
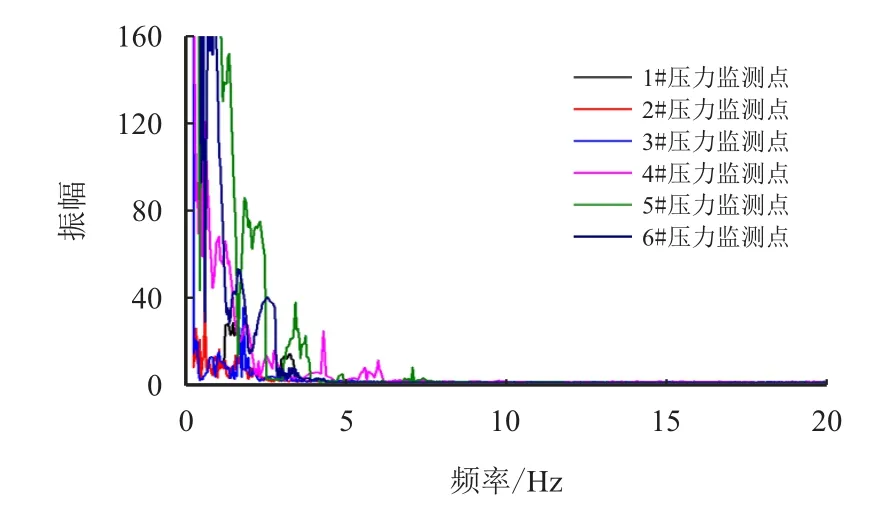
图16 整改后流体压力波动频谱图Fig.16 Spectrum of fluid pressure fluctuation after rectification

图17 整改后工况三振动速度Fig.17 Vibration speed of working condition III after rectification
由图16 可以看出,与改管前相比,相同工况下的管道内压力波动频率稍有降低,但总体变化不大,压力波动依旧集中在低频范围内,但由于新增加了锚固墩和管夹约束,管道系统的固有频率已得到提高,避开管道内压力波动的频率范围。因此,管道系统不会再出现共振现象。
从图17 可以看出,方案二的减振效果最佳,按照《压缩机管道振动控制标准》,其管道振动水平评估均为优秀。
3 结论
1)模态分析和管道内流体压力波动频谱表明,流体压力波动频率与管道系统的低阶固有频率接近,从而发生共振现象,使振动变得更加剧烈。多工况流固耦合分析结果表明,管道的异常振动现象与管内输气量密切相关,在流体流速突然变低的三通附近形成强烈的涡流波动,进而产生流体激振力,引起管道振动。
2)基于流固耦合方法,能够准确找到管道振动强烈位置,并能对压气站运行给予合理建议。当压气站采用联合运行方式时,推荐联通管线全部开启,以避免单根联通管线工作,导致该联通管内输气量过大,从而在管道内产生强烈的流体激振力,引发管道振动。
3)提出了减缓管道异常振动的两种方案,模拟表明,同时增大管径和增加适当约束的方案最佳,按照此方案整改之后的站场管道即使在极为恶劣的工况三下,管道的振动水平也能被控制在优秀范围内。

