高温高产井井口抬升及下沉风险分析研究

王雪刚，魏瑞华，张 浩，于 浩 ，赵朝阳

1.中国石油新疆油田分公司工程技术研究院，新疆 克拉玛依 834000；2.中国石油新疆油田分公司勘探事业部，新疆 克拉玛依 834000；3.油气藏地质及开发工程全国重点实验室·西南石油大学，四川 成都 610500

引言

井口抬升通常是指生产井在生产过程中井口装置出现整体轴向抬升的现象[1]。近年来，随着高温高压高产的油气田开始广泛开发，井口抬升现象已经普遍出现在国内各大油田[2-3]，导致油气井产量下降和关停，严重影响正常生产作业。由于高温高压高产井存在试油产量高、地层环境复杂等特点，在生产过程中极易发生井口抬升的风险，为保障生产作业正常进行，因此，亟需开展井口安全风险预测研究。

国内外许多学者对井口安全问题进行了大量研究。其中，桂烈亭等[4-5]以传热学和两相流理论为基础，建立了井筒温度场的二维数学模型；李伟超等[6]针对稠油热采井吞吐传热现象，提出了井筒综合传热系数的计算方法；卢亚锋等[7]发现多层套管固井质量差时对井口装置抬升高度影响较大；张春杰等[8]等针对表层套管固井期间出现的井口下沉现象，提出应实时调整大钩悬重，避免增加的径向载荷作用至井口；林元华等[9]提出了基于粒子群多目标优化算法的一种新的井口装置抬升高度预测方法；Gao 等[10]发现固井质量差是造成地面套管水泥环失效的最主要原因。张智等[11-12]提出多层套管同时存在自由段时，环空热膨胀压力不会改变多层套管自由端长度对井口抬升的影响；Qiao 等[13]提出生产过程温度和压力效应引起的井口增长可能会损害井的完整性。李军等[14]针对全井固井条件下渤海油田稠油热采井套管-水泥环在生产之间的摩阻，建立了井口抬升距离预测模型；石小磊等[15]建立了多因素作用下井口抬升高度预测模型，发现套管材料的热理性是井口抬升的关键因素；Wang 等[16]考虑材料力学非线性特性，提出了一种预测深水井井口增长潜力的模型；王汉等[17]基于井筒对管柱力学理论，发现井筒温度效应和自由套管长度是导致井口抬升的关键因素；谢仁军等[18]发现随温度的增加，井筒各层管柱的抬升量与温升呈线性增长；童传新等[19]建立了深水窄安全压力窗口井筒压力控制模型，并在此基础上提出深水精细控压下套管方法；张广清等[20]发现随套管偏心率的增加及水泥环缺陷，水泥环完整性逐渐降低；郑双进等[21-22]提出井筒温度升高及其引发的圈闭压力是造成深水高温高压井井口抬升的两大主要因素。

根据以上学者研究结果，目前，主要采用生产管柱隔热处理、自由段套管挤水泥封固作业、预应力方式完井及热应力补偿器等措施来预防井口抬升现象的发生。然而由于实际井口抬升现象受水泥返高、井身结构及地层温度等诸多因素共同影响，以上措施均不能达到预期要求。因此，本文根据多级传热理论，利用有限元方法，针对不同作业过程井筒管柱受力特点，通过生死单元技术提出一种全新的井口抬升预测方法，同时以X1 井为例，建立了井筒管柱井口抬升计算模型，从下套管-固井-油气生产全阶段开展井口抬升研究，对实际现场井口抬升预测以及防控措施的制定具有一定指导意义。

1 井口抬升机理及多级传热理论

1.1 多级井筒传热理论

对于高温高压生产井而言，各级套管、水泥环与地层呈现多级传热系统，然而由于套管、水泥环和地层的热力学参数不同，导致整个温度剖面呈现非线性关系，而水泥环的缺失情况会使温度剖面变得更加复杂。新疆油田南缘区块位于准噶尔盆地南部，该区块油藏普遍埋深超过8 000 m，压力高于140 MPa，温度为160°C。其中，X1 井为某区块高产井，实际产油量为2 349.6 t/d，产气量为148.9 m3/d，地层地温梯度为1.86°C/hm。油层中部垂深4 720.7 m，属于典型的复杂地层高温高压高产井。以X1 井为例，多级圆筒壁稳态导热示意图如图1 所示。

图1 多层圆筒壁稳态导热示意图Fig.1 Steady-state heat conduction diagram of multilayer cylindrical wall

可将X1 井各级套管、水泥环及地层导热率分别视为λ1、λ2和λ3，内、外壁面维持均匀恒定的温度tw1、tw2、tw3及tw4。由于通过各层圆筒壁的热流量相等，且总导热热阻等于各层导热热阻之和。因此，单位长度圆筒的导热热流量为[23]

式中：ϕl—单位长度圆通的导热热流量，W；

Rλi—多层圆筒壁中第i层圆筒壁的导热热阻，°C/W；

ri—第i层圆筒壁的半径，m；

λi—多层圆筒壁中第i层圆筒的导热率，W（/m·°C）；

twi—多层圆筒壁中第i层圆筒内外壁面的温度，°C。

以此类推，对于多层不同材料组成多层圆筒壁的稳态导热，单位长度圆筒的导热热流量为

式中：n—多层圆筒壁的总层数。

1.2 井口抬升机理分析

由于套管是具有热理性的金属材料，在温差作用下会产生一定线膨胀，形成套管轴向伸长和径向形变，在套管端部产生轴向位移。当套管端部受井口约束限制或受到水泥石胶结作用导致套管不能自由伸长，套管产生应力重新分布，使套管产生轴向作用力。当轴向作用力大于套管重力及水泥石胶结作用力和井口重量等外载时，套管将举升井口，出现井口抬升现象，井口抬升力学模型如图2 所示。

图2 井口抬升示意图Fig.2 Wellhead lifting diagram

对于生产井而言，井筒温度随着实际生产作业中产量的升高而增加，当井筒产量及温度一定时，其套管线膨胀计算公式为

式中：

ΔL－套管轴向线膨胀量，m；

ε—温度应变，无因次；

L—管柱长度，m；

α—套管热膨胀系数，°C-1；

ΔT－温度变化，°C。

井口套管热膨胀效应对井口产生的作用力为

将式（3）代入式（4），得

式中：

Ftj—第j层套管热膨胀时对井口产生的作用力，N；

σj—第j层套管井口热膨胀应力，Pa；

Aj—第j层套管材料井口的横截面积，m2；

ΔLj—第j层套管井口热应变，m；

Lj—第j层套管长度，m；

αj—第j层套管热膨胀系数，°C-1；

ΔTj—第j层套管温差，°C；

Ej—层套管材料的弹性模量，Pa。

2 井口抬升计算方法及模型的建立

2.1 计算方法

按照实际作业顺序，可将油井各层套管分为初始阶段、下放阶段、固井阶段和生产阶段。在下放阶段，各级套管在自重以及摩阻合力作用下会发生一定伸长，并产生一定预应力，随着固井作业中水泥浆完全凝固，会对管柱产生相应的封固作用，同时，将各级套管在下放阶段所产生的伸长量及应力状态封固在地层中；在生产阶段，由于井筒温度上升，各级套管随之产生一定热应力和热膨胀量，与预拉应力共同作用下，使得套管上应力状态发生变化。当温度产生的热应力大于固井作业完成后套管预拉应力时，套管井口处出现抬升风险。

关于井口抬升计算，常规方法主要依靠解析法，但该方法忽略了非线性传热过程对套管应力的影响，不能准确反映套管真实的伸长量，对于井身结构和受力复杂的工况，其结果往往误差较大。为还原地层各级管柱在不同阶段受力情况，本文基于多级传热理论及有限元数值方法，利用生死单元技术提出一种全新的井口抬升计算方法，井口抬升计算流程如图3 所示。

图3 井口抬升计算方法流程Fig.3 Flow of wellhead lifting calculation method

1）自重伸长：当套管在井筒中下放到位时，井口套管头受到采油树的约束，同时由于浮重作用，管柱会发生一定程度的初始伸长，故在模型中将套管井口位置轴向约束，并对该井段管柱施加一定浮重及摩阻，最终计算套管在浮重及下放摩阻作用下自由伸长量。

2）固井阶段：由于水泥浆凝固后会将管柱在浮重作用下产生的拉伸应力及伸长量封固在地层中，并与之形成一个整体。首先，本文通过使用生死单元技术，在固井阶段恢复了地层及水泥环位置处网格，以还原固井后水泥环对套管柱之间封固作用。其次，为避免出现网格畸变现象，借助任意拉格朗日-欧拉自适应网格（Arbitrary Lagrangian-Eulerian）方法对固井作业后模型的网格形态进行调整。在该阶段中除了保持管柱顶部约束不变之外，还应对所有套管底部施加一定轴向约束，以保证下放阶段钻柱应力状态可持续存在于固井阶段。最后，开展井筒管柱在固井状态有限元分析。

3）生产阶段：在生产过程中，由于产量的不同，井筒温度分布状态随之不同，管柱所产生的热膨胀量及热应力也相应变化。根据生产过程中井筒流体在流向井口过程中的温度分布，结合实际地层地温梯度，开展多级套管-水泥环-地层热传递过程及温度场诱发井口抬升分析。在远端地层施加原始地层温度梯度前提下，根据生产过程在井筒内壁上施加相应井筒温度变化曲线。此外，为获得生产过程中各级套管对井口的支反力，首先，对套管井口位置进行约束，其次，结合实际井口装置重量解除井口位置约束，最终，获取井口抬升高度。

2.2 有限元模型的建立

X1 井为新疆油田某区块新开发的一口高温高压高产水平井，实际现场作业测试显示，该井井深4 600.00 m 位置处地层温度为124.38°C。其井身结构如图4 所示。

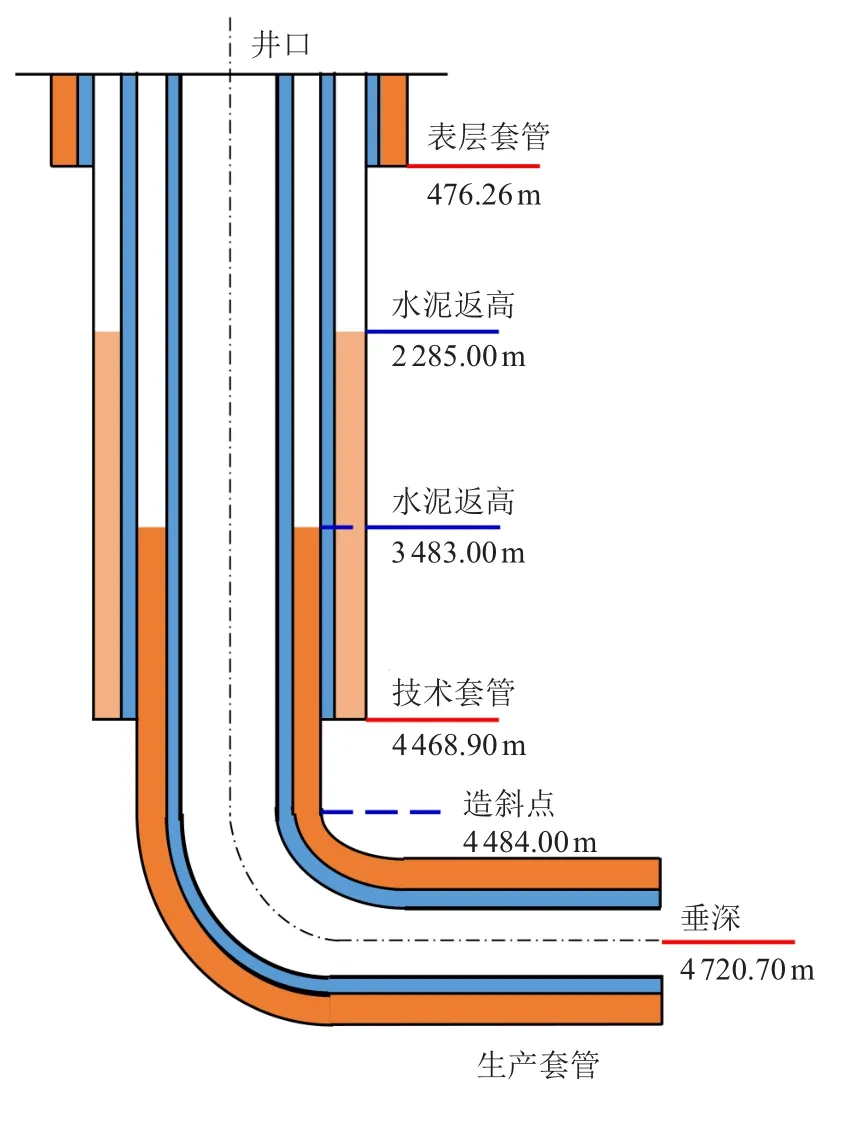
图4 X1 井井身结构示意图Fig.4 Schematic diagram of well body structure in Well X1

X1 井实际井深为5 528.00 m，垂深4 720.70 m，最大井斜角可达89.33°。其中，造斜点位于井深4 484.00 m 处。此外，该井采用油层套管作为生产管柱，表层套管、技术套管、油层套管外径分别为339.70、244.50 及139.70 mm，环空水泥返高分别至井口、2 285.00 及3 483.00 m 处。因为油层套管和技术套管环空水泥返深高度均较小，导致油层套管、技术套管存在较大长度的自由段管柱。由于缺少水泥环提供的封固作用，加之该井实际产量较高，当生产过程中产量发生波动，自由段管柱极易在温差作用下发生热膨胀现象，最终使得油井井口发生抬升。

根据X1 井井身结构，针对垂深为4 484.00 m 以上井段，建立多层套管-水泥环-地层多体系热固耦合轴对称模型。该模型轴向总长4 484.00 m，横向为10 m，其中，各级管柱、水泥环及地层力学参数见表1所示。由于纵横比较大，为了显示更为清楚，将模型横向系数放大4 000 倍，如图5 所示。为了保证计算结果精确性，采用渐变布种的方式实现井筒附近计算网格的加密。而在计算过程中，在提取不同生产工况下各管柱井口位置的作用力及轴向位移后，通过将各级管柱井口位置耦合至一点，还原井口装置对各级套管柱的耦联作用，实现了生产过程中各级管柱之间的相互影响，最终获取了不同生产过程中油井井口的整体抬升位移及整体支反力。

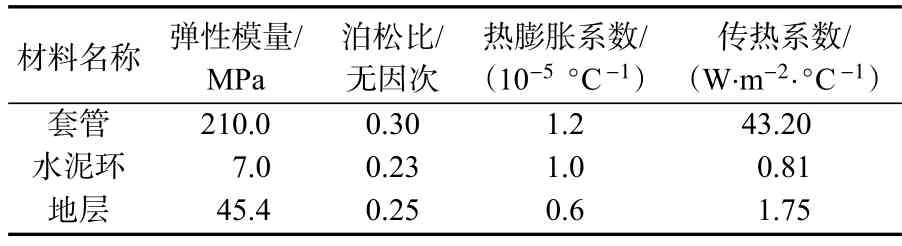
表1 X1 井地层管柱-地层-水泥环力学参数Tab.1 Formation string-formation-cement sheath mechanical parameters of Well X1

图5 多层套管-水泥环-地层多体系统热固耦合有限元模型Fig.5 Thermal-structure coupling finite element model of multilayer casing-cement-formation multibody system

3 井筒数值分析

3.1 下放过程井筒管柱数值分析

管柱的应力状态对井口抬升现象的发生影响显著。对于井眼轨迹复杂的水平井来说，在下放过程中，除自重作用外，套管同时还承受一定的下放摩阻和流体浮力。当下放摩阻和流体浮力较大时，套管拉伸情况明显减缓，在生产状况下，随着温度所产生的热应力大于管柱原有拉伸应力时，井口位置处会发生抬升。因此，为准确计算X1 井井口抬升情况，需保证下放过程中管柱应力状态精确性。图6 为X1 井管柱下放过程中井口大钩载荷变化情况，可以发现在造斜点以后，实际大钩载荷减少212 kN，即表明管柱在水平段下放过程中摩阻大小为212 kN。

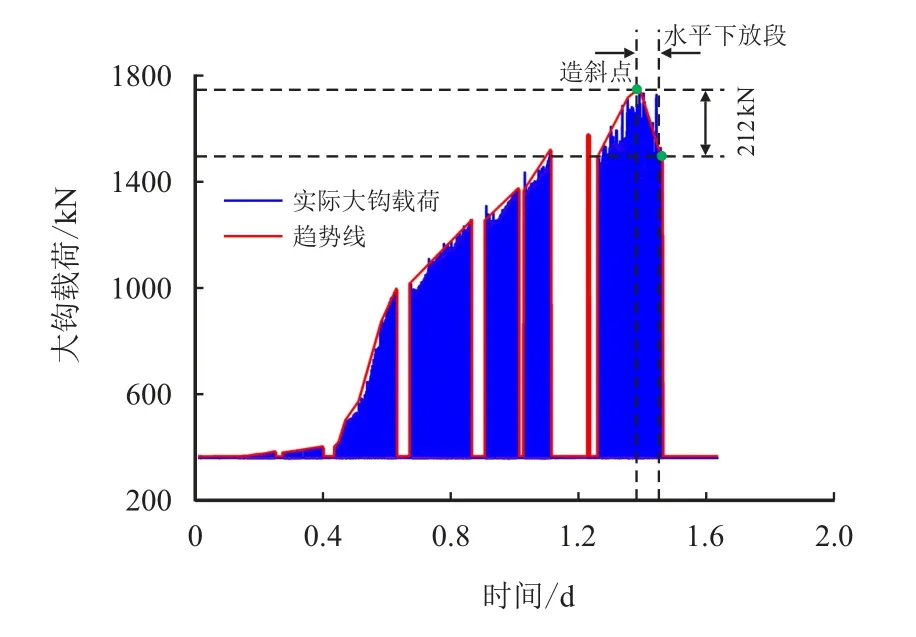
图6 X1 井管柱下放过程中井口大钩载荷变化曲线Fig.6 Load variation curve of wellhead hook during Well X1 string lowering

各级管柱下放过程中应力及轴向位移分布云图如图7所示，其中，井筒各级管柱最大应力都位于井口，最大轴向位移都位于井底处，油层套管、技术套管以及表层套管上最大应力分别为284.3，284.2 和29.6 MPa；最大轴向伸长量分别为2.80，2.78 和0.03 m。此时井筒管柱在井口的支反力分别为1 120.0、2 289.7 和278.8 kN。

图7 下放过程中井筒管柱应力及轴向位移分布云图Fig.7 Contour of wellbore string stress and axial displacement distribution during lowering process

3.2 固井后井筒管柱数值分析

通过生死单元技术将地层和水泥环恢复，以还原固井后井筒各级管柱分布状况。固井后，由于井筒水泥浆凝固后对井筒管柱存在一定封固作用，即各级管柱与地层形成新的整体，从而将拉伸状态下的各级管柱封固在地层中，各级管柱上应力及其伸长量不会发生变化。此时，固井后各级管柱应力及位移分布云图如图8 所示。

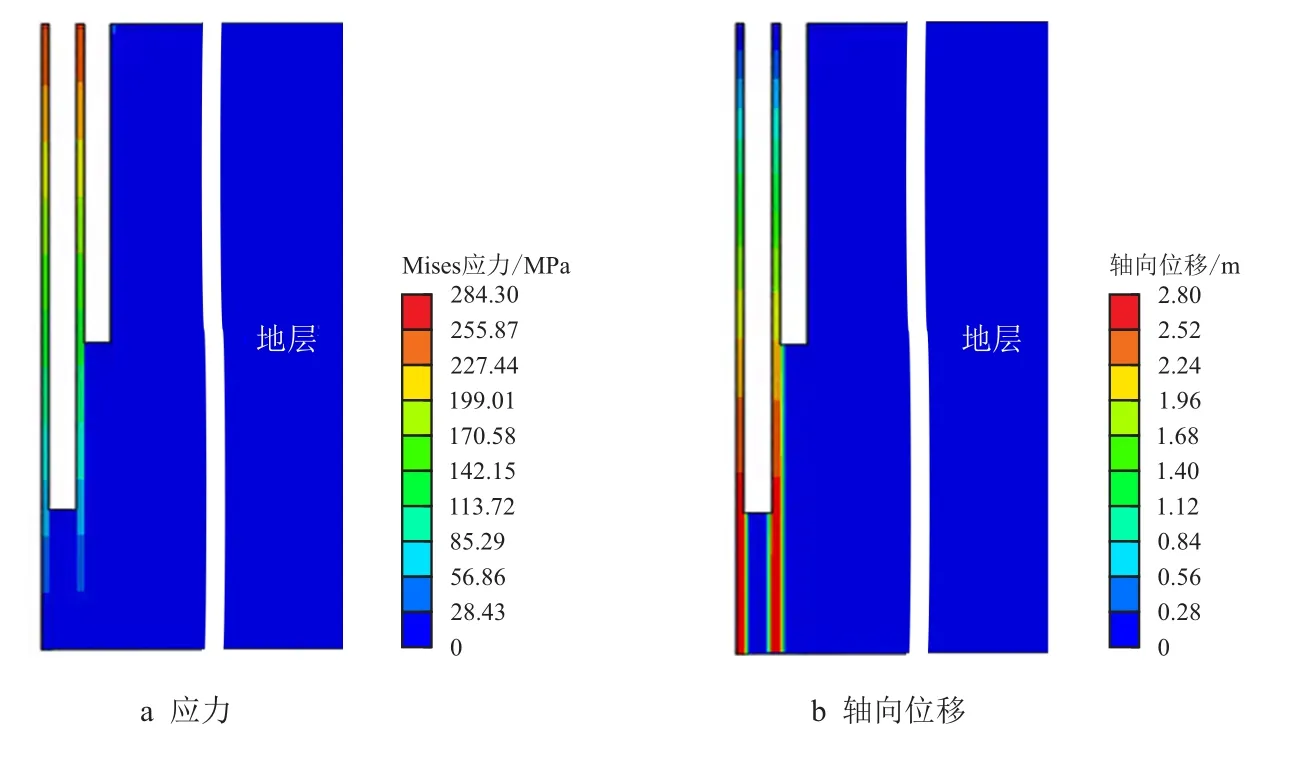
图8 固井作业后各级管柱应力及轴向位移分布云图Fig.8 Contour of stress and axial displacement distribution of each string after cementing operation

3.3 不同生产工况下各级管柱数值分析

3.3.1 正常生产工况

图9 为正常生产工况下地层温度场及各级管柱应力和轴向位移分布云图，在正常生产过程中该井油层套管井口温度为98.6°C，井底温度为138.1°C。生产过程中井筒内温度剖面曲线如图9a所示。从图9a 可知，在径向上从油层套管向远端地层温度开始逐渐降低。由于X1 井存在大段无水泥封固段管柱，无法有效抑制不同载荷下管柱的变形情况，在生产过程中，未封固段管柱会发生一定轴向收缩。当井口无压重时，X1 井各级管柱应力及轴向位移分布云图如图9b 所示，由于下部水泥环约束作用，各级管柱最大应力及轴向位移仍位于其管柱底部，大小分别为278.6 MPa、2.8 m。在水泥未封固段管柱底部应力明显增大，表明该处套管此时受到一定的压力。此时井口处的油层套管、技术套管以及表层套管相对于初始状况产生回缩趋势，回缩量分别可达0.53，1.13 和0.01 m，同时各级管柱井口位置分别产生100.2，577.4 和139.4 kN 的下拉力。当井口装置压重为9 t时X1 井各级管柱应力及位移分布云图如图9c 所示。可以发现，当井口存在大小为90 kN 的载荷时，由于水泥环的封固作用，最大位移仍位于井底处，大小为2.8 m。相对于井口无压重状况下，此时未封固段各级管柱轴向压缩情况更为严重，井口处油层套管、技术套管以及表层套管收缩量分别增加至0.92，1.32 和0.01 m。根据以上结论可知：在正常生产作业中，当各级套管由井口装置耦联在一起时，无论是否存在井口装置压重，X1 井都不会产生井口抬升。

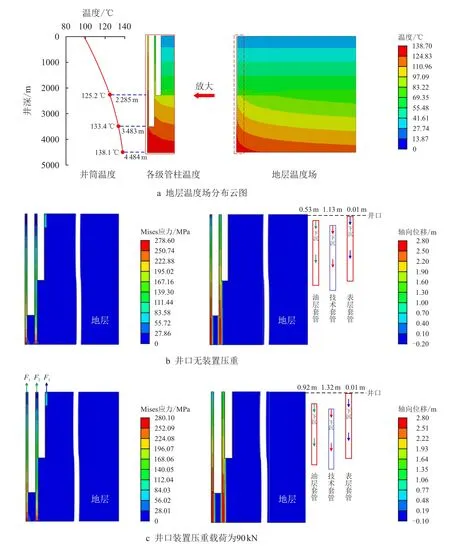
图9 正常生产工况下地层温度场、各级管柱应力及轴向位移分布云图Fig.9 Contour of formation temperature field,stress and axial displacement of wellbore string in normal production process

3.3.2 极限生产工况

随着产量的上升，井筒温度会急剧增加。在极限生产工况下，即生产过程中井筒管柱井口温度升至117°C时，地层温度场及各级管柱应力和位移如图10 所示。从图10a 可知，相对于正常工况下，地层各级管柱温度明显较高，其中，技术套管及表层套管温度增加幅度明显较大，造成各级管柱产生的热膨胀量及热应力也相应增加。当井口无压重时，各级套管应力及位移分布云图如图10b 所示。在水泥环封固作用下，地层管柱上最大位移发生部位及大小并未发生变化，大小仍为2.8 m；但最大应力减小至281.3 MPa。同时，油层套管及表层套管井口位置分别产生28.2，467.2 kN 的上顶力，形成一定抬升趋势，但表层套管在水泥环封固作用下，最终并不会发生抬升现象。与油层套管相反，随着生产过程中技术套管上产生的热应力并未完全消除管柱原有预拉应力，最终导致管柱产生回缩趋势，回缩量可达0.9 m，并产生754.7 kN 的拉力。

图10 极限生产作业过程中地层温度场、管柱应力及轴向位移分布云图Fig.10 Contour of formation temperature field,stress and axial displacement of wellbore string during extreme production operation

当井口装置压重载荷为90 kN 时，各级套管应力及轴向位移分布云图见图10c 所示。由于井口装置自重对各级管柱产生一定的下压作用，使得此时油层套管和技术套管顶部产生分别产生大小为0.38，1.10 m 的回缩量，然而，由于表层套管水泥环的约束作用，此时表层套管井口位置并未产生任何位移。

按照实际作业过程中各级套管在井口处被井口装置耦联在一起时，当井口装置无压重时，各级管柱对井口产生704.1 kN 的整体上顶力，而当井口装置压重载荷为90 kN 时，各级管柱对井口产生614.1 kN 的整体上顶力。然而，由于表层套管环空水泥环无缺失，在表层套管环空水泥环约束作用下，最终造成井口整体并未出现抬升现象。

在极限工况下，由于表层套管对环空水泥环的封固作用，使得X1 井井口不会出现整体抬升风险。为了验证表层套管水泥环对井口抬升的影响，开展了表层套管水泥环缺失100 m 时的井口抬升风险分析。

图11 为表层套管水泥环缺失100 m 时地层温度场及各级管柱应力和位移云图，从图11 可知，地层温度大小及分布并未发生明显变化，由于表层套管环空水泥环存在100 m 缺失，地表100 m 地层温度明显下降。相对于表层套管未缺失情况，当表层套管水泥环存在100 m 缺失，在生产过程中，表层套管产生的热膨胀及上顶力未得到水泥环封固，除表层套管外，油层套管和技术套管的最大应力和最大轴向位移分布都未发生变化。在井口装置无压重时，表层套管发生抬升，抬升量为0.1 m，并对井口产生652.6 kN 上顶力。在井口装置存在大小为90 kN 的压重载荷时，由于压重作用，表层套管抬升量仅为0.1 m，表层套管上顶力减小至562.6 kN。

当各级套管耦联成一整体时，在不考虑井口装置压重时，各级管柱对井口产生213.6 kN 整体上顶力，同时井口整体发生抬升，抬升量为0.03 m。井口装置所提供的载荷为90 kN 时，生产过程中油井井口将产生123.6 kN 整体上顶力，井口抬升量整体减小至0.02 m。从上可知，当表层套管发生缺失时，X1 井存在井口抬升风险。

图12 为X1 井井口支反力分布示意图。根据不同工况下X1 井各级管柱井口风险评价分析，得到不同工况下各级管柱井口支反力和轴向位移如表2、表3 所示。可以明显发现：在正常生产工况且不考虑井口装置的耦联作用时，由于井筒存在较长自由段管柱，使得技术套管和油层套管井口位置都存在一定回缩趋势，在井口装置压重作用下，除表层套管因水泥环的封固作用井口位置保持不变，技术套管与油层套管的回缩趋势都得到一定加强，最终该井并不会发生井口抬升现象。当处于极限生产工况且表层套管水泥环无缺失时，在不考虑井口装置压重及耦联作用下，除技术套管外，表层套管和生产套管都存在一定的抬升趋势，当井口装置耦联各级套管后，由于表层套管水泥环的封固作用，该井仍不会发生井口抬升现象。但当表层套管水泥环缺失100 m 时，表层套管所受水泥环封固作用下降，此时不能有效约束井筒管柱在温差和重力作用后所产生的剩余应力及位移，该井最终发生井口抬升现象。结果表明，存在较长自由段管柱的油井在高产量工况下存在一定的井口抬升风险，而井口装置的压重会抑制井口的抬升趋势，但表层套管水泥环质量直接决定井口抬升现象的产生。

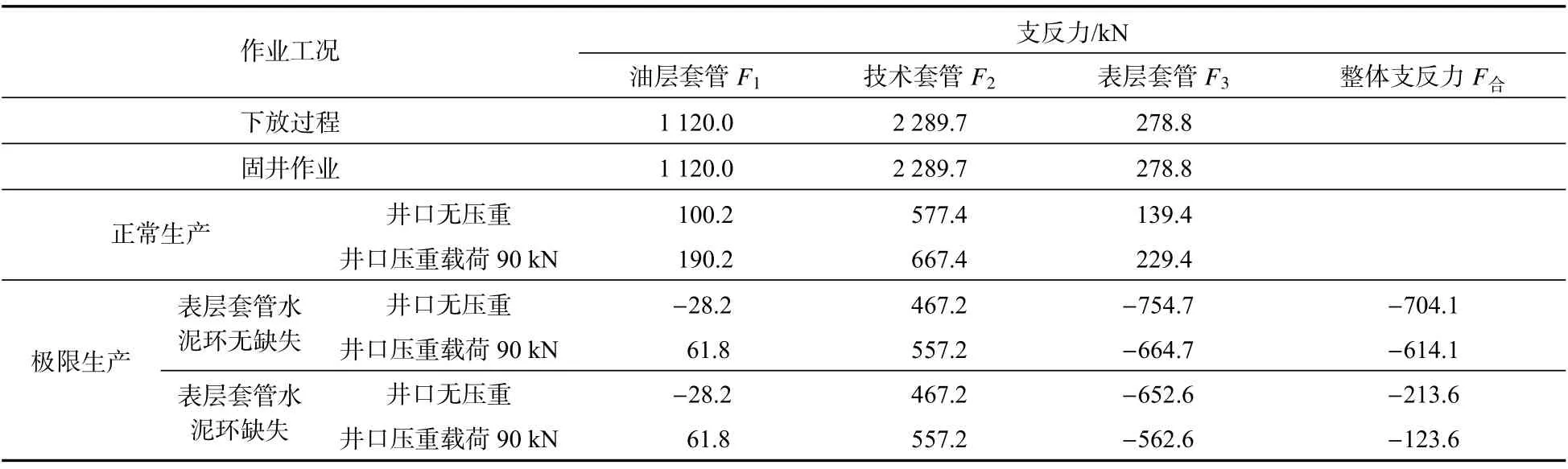
表2 不同工况下各级管柱井口支反力（正值为下拉力、负值为上顶力）Tab.2 Wellhead reacting force of all strings under different working conditions（positive value is down force,negative value is up force）

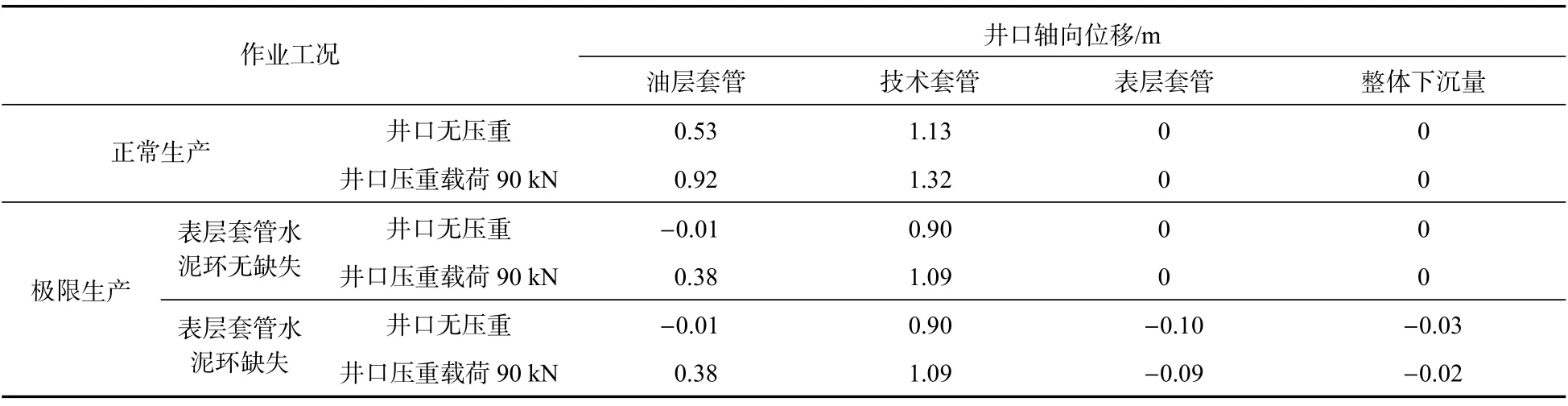
表3 不同工况下各级管柱井口轴向位移（正值为下沉，负值为抬升）Tab.3 Wellhead axial displacement of each string under different working conditions（positive value is subsidence,negative value is uplift）

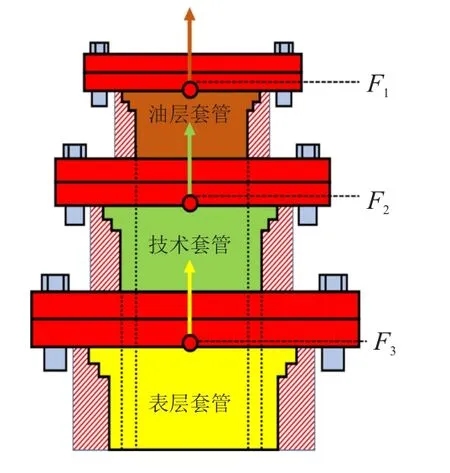
图12 X1 井井口支反力示意图Fig.12 Schematic diagram of wellhead support reaction in Well X1

4 结论

1）利用生死单元技术提出了一种全新的井口抬升计算方法，并以X1 井为例，根据其井身结构及生产情况，建立了各级管柱-水泥环-地层热固耦合有限元分析模型，最终得出该方法可以有效适用于高温高压高产井井口抬升风险评价分析研究。

2）正常生产作业下，X1 井井口并不会出现井口抬升现象，此时井筒管柱最大伸长量和应力都位于井底处。在极限工况下，当表层套管水泥环质量较好时，由于水泥环的封固作用，并不会产生抬升现象。当环空水泥环存在缺失时，井口发生整体抬升现象，井口无压重下，井口整体抬升量为0.03 m，井口存在大小为90 kN 的压重载荷时，井口整体抬升量减小至0.02 m。

3）为降低实际生产过程中井口抬升风险，在合理注采的前提下，应尽量提高生产套管、技术套管水泥返高。同时需保证表层套管水泥环返至井口位置且具有较好的固井质量，以防止生产过程油井井口发生抬升现象。