基于ANSYS－Workbench的4BM－250型苎麻剥麻机机架有限元分析与结构优化

刘佳杰，马兰，向伟，颜波，段益平，文庆华，吕江南

(中国农业科学院麻类研究所，湖南长沙 410221)

苎麻俗称“中国草”，在我国已有4700 多年的种植历史，是一种重要的纺织原料[1]。目前，我国苎麻总产量约占世界总产量的90%以上[2－3]。苎麻为多年生植物，生物产量较高，一次栽种，多年收益，通常一年可以收获3 次[4]。与其他纤维相比，苎麻纤维作为纺织材料原料有着独特的优势:吸湿、透气、导热快、质地轻、静电少、防虫防霉、耐磨性好[5]。苎麻纤维作为优质的纺织原料有许多独特的天然特性，但苎麻纤维的剥制提取却十分困难。苎麻纤维剥制加工存在成本高、劳动强度大、作业效率低及剥制质量不稳定等问题，迫切需要研制出高效苎麻剥麻机，解决长期制约我国苎麻产业发展的“剥麻难”问题。

1981年我国第一台动力剥麻机6BZ－400 的问世，标志着我国苎麻纤维剥制进入了机械动力时代。之后涌现出了多种机型剥麻机械，按照剥制原理与结构形式主要分为3 种:人力反拉式剥麻机、直喂式剥麻机和横向喂入式剥麻机[6]。其中，人力反拉式剥麻机按照剥制滚筒的数量又可以分为单滚筒和双滚筒式剥麻机，这种类型剥麻机依靠手工喂入和人力反拉方式依次完成苎麻稍部和基部纤维的剥制。主要代表机型有:6BM－350 型剥麻机、6BM－400 型剥麻机、4BM－260 型剥麻机、4BM－240 型剥麻机等。人力反拉式剥麻机机型结构紧凑、工作稳定、移动灵活、剥麻质量较好，原麻含杂率均低于1%，鲜茎出麻率均超过5%，作业效率为8～15 kg/h，为手工剥麻效率的3～5倍。这种机型的缺点是加工劳动强度大，操作安全性差。横向喂入式剥麻机采用苎麻茎秆横向喂入、分段连续刮麻的设计原理剥麻。这类机型剥麻机机型巨大、结构复杂、能耗较高，适合企业大规模化生产作业需求，但存在两个主要问题:一是剥麻损失率较高，二是剥麻质量不稳定。到目前为止，横向喂入式苎麻剥麻机在苎麻纤维的剥制加工中鲜见使用。直喂入式苎麻剥麻机将待剥苎麻茎秆沿喂入滚筒旋转切线方向纵向喂入，通过多组不同结构形式差速滚筒对苎麻茎秆进行反复碾压、弯折、揉搓和刮打实现纤维剥制。主要机型有中国农业科学院麻类研究所研制的4BM－450型直喂式苎麻剥麻机和华中农业大学研制的JBM－100 型直喂式剥麻机。该类机型操作简单，加工劳动强度低，操作安全可靠，可实现连续剥麻作业，生产效率高，作业效率约30 kg/h，鲜茎出麻率甚至可超过7%，但所剥制的纤维存在基部麻骨较高和剥制不净等问题。目前生产上主要应用的机型依然是双滚筒反拉式苎麻剥麻机。为了提高剥麻机喂麻时的舒适性与安全性并减轻总体重量，在4BM－260 型苎麻剥麻机的基础上改进设计，成功研制了4BM－250 型苎麻剥麻机。

为避免剥麻机工作过程中机架出现结构强度不足和共振问题，运用计算机Solidworks 软件建立4BM－250 型苎麻剥麻机机架的三维模型，简化后导入至ANSYS－Workbench 中，对剥麻机机架进行静力学分析与模态分析。通过静力学分析获得剥麻机机架在静载荷下的最大位移和最大应力，通过模态分析获取机架的固有频率及其相对应的振动类型，并与外部激励频率进行比较，对机架的设计提出改进措施。

1 4BM－250 型苎麻剥麻机整体结构与工作原理

4BM－250 型苎麻剥麻机的主要结构包含喂料斗、剥麻装置、机架、动力系统、行走装置、接麻装置、机罩等。该机械主要工作原理是针对苎麻韧皮纤维柔韧有弹性，而麻骨脆硬易断裂的力学特性差异，利用高速旋转的滚筒将麻骨击碎并将其从纤维上刮除，进而获得原麻纤维。4BM－250 型苎麻剥麻机整机结构如图1(a)所示，剥麻机机架结构如图1(b)所示。其主要技术参数如表1所示。

表1 4BM－250 型苎麻剥麻机主要技术参数Table 1 Main technical parameters of 4BM－250 ramie decorticator

2 4BM－250 型苎麻剥麻机机架静力学分析

2.1 静力学分析理论

静力学分析主要用于研究机构部件在静载荷作用下的结构响应，如结构的变形、应力及应变等。机构部件在受到静态载荷的作用时，惯性和阻尼可以忽略[7－8]。在剥麻机作业过程中，机架受到上、下剥麻滚筒及柴油机组的重力作用，因此基于有限元静力学理论方法对剥麻机机架进行分析，可以得到机架在静载荷作用下的应力、位移、变形分布情况，从而找到机架的薄弱位置，为机架的设计优化提供参考。根据静力学分析理论:机架产生的弹性变形，力与位移应满足如下关系[9]:

式中:[K]—系统结构的刚度矩阵；[δ]—系统节点的位移矩阵；[F]—系统受总载荷矩阵。

2.2 有限元模型的建立及网络划分

机架是剥麻机的主要承载结构，主要的承载部件为剥麻机上、下剥麻滚筒部装及柴油机组，其主要由17 根主梁和两个可调节伸缩支撑脚组成。17 根主梁采用焊接方式连接，主梁与可调节支撑脚之间采用螺栓连接。机架的整体结构刚度对整机的工作性能至关重要。为了使计算更加准确，对模型进行简化，忽略对结果影响不大的因素，如将螺栓孔侧板等去除。简化后机架结构模型如图2(a)所示。

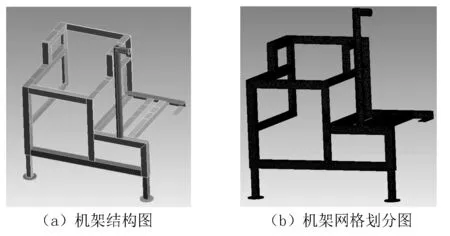
图2 机架结构图及网格划分图Fig.2 Frame structure diagram and mesh division diagram

将Solidworks 软件中的有限元模型导入至ANSYS Workbench 中，选择好材料属性，设置好接触类型，对模型进行网格划分，选取合适的网格尺寸可以保证分析结果的准确性。按照有限元分析的原理，模型网格划分越密，计算精度越高。考虑到工程实际问题，随网格划分密集程度加大，计算成本、求解时间和计算机的储存空间都会大幅增加，因此在实际计算中选择满足计算精度的网格即可。本文选择Tetrahedrons 网格形式对模型进行划分，同时将网格单元尺寸设置4 mm，生产网格节点925 715 个，网格单元534 631 个。机架网格划分图如图(b)所示。

2.3 边界条件设置、求解与结果分析

4BM－250 型苎麻剥麻机采用2.8 kW 电启动柴油机。对剥麻机机架进行受力分析，将柴油机组及上、下剥麻滚筒的等效重力加载到剥麻机整体机架安装位置上，通过Solidworks 软件的评估质量属性模块测量上、下剥麻滚筒部装的质量。机架整体的受压力情况如表2所示。

表2 机架整体所受压力情况Table 2 The overall pressure on the frame

经过计算机软件的求解计算，机架受载下总位移及应力云图如图3所示。分析图3 可知，机架的最大变形处发生在接麻杆最上部位置，最大变形量为0.14 mm，最大应力为23.71 Mpa。机架材料选择Q235 结构钢，最大屈服极限强度为235 Mpa。为避免机架在正常作业时发生疲劳失效，设置安全系数，许用应力公式如式(2)。

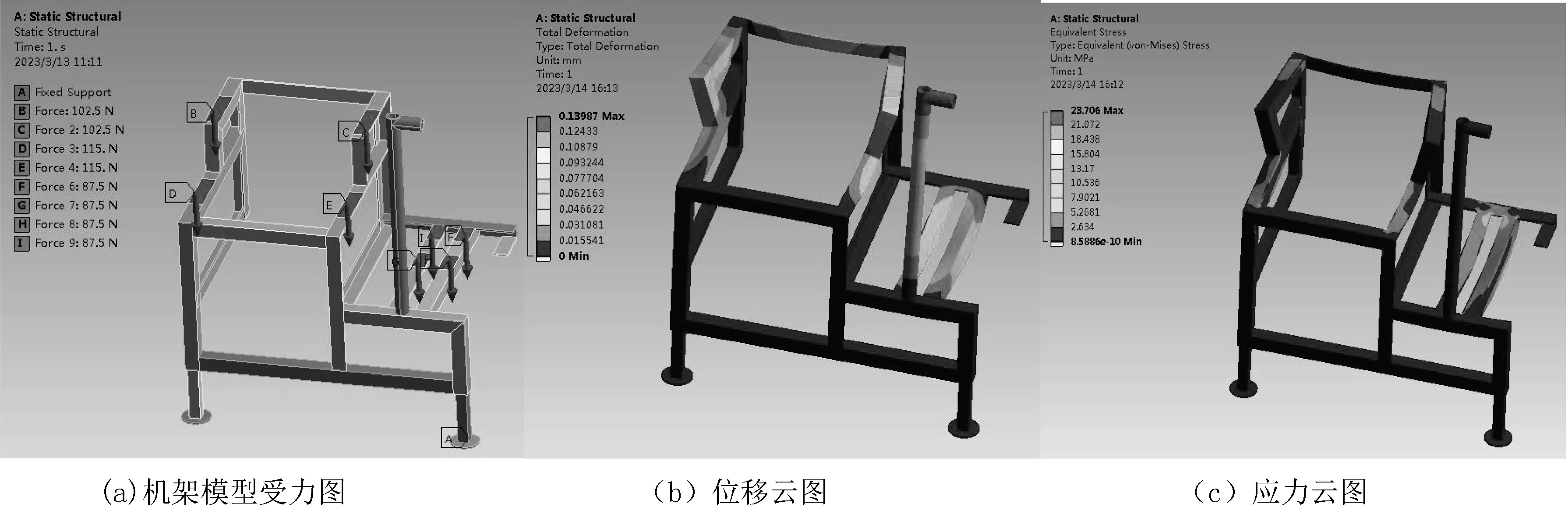
图3 机架模型受力图、位移云图及应力云图Fig.3 Frame model stress diagram，displacement cloud diagram and stress cloud diagram

式中:[σ]为取安全系数后材料的屈服强度，Mpa；σn为机架材料的屈服强度，Mpa；n为安全系数，取1.5。

计算得出机架在加载后所受到的应力为23.71 Mpa，低于材料的屈服强度156.67 Mpa。故此机架结构在条件载荷下的强度和刚度满足设计要求。

3 4BM－250 型苎麻剥麻机机架模态分析与结构优化

3.1 有限元模态分析理论

模态是机械结构的固有属性，由结构自身材料以及力学性能决定，与结构外激励无关[10]。模态分析是机械工程振动领域研究结构动力学性能及进行结构振动优化的基础方法。在进行结构振动诊断及原因分析之前，对结构部件进行模态分析有助于评价现有结构系统的动态特性。由振动理论可知，有阻尼N 的自由度系统的强迫振动方程可以表示成公式(3):

式中:M—质量矩阵；C—阻尼矩阵；K—刚度矩阵；x—位移矢量；f(t)—外载荷。在计算固有振动特性时，考虑到结构阻尼较小，对结构的固有频率和振型影响较小，因此假定整体框架做自由振动并且忽略其阻尼。则有公式(4):

由振动理论可知，任何振动都是由一系列简谐振动叠加而来，则式(4)的解可表达为:

式中:t—时间，s；Wi为第i阶固有频率值，Hz；Φi为结构振型在第i阶固有频率下的特征向量。联合公式(4)和(5)可推出公式(6):

由公式(6)可计算得出结构的固有频率W1、W2、W3……Wn及对应的模态Φi。

3.2 机架有限元模态分析

在机架设计时，为避免共振问题，需要确定刀架的固有频率和振型。模态分析是求解固有频率和振型的有效方法，因此在设计阶段有必要对零部件进行模态分析。为了全面地了解4BM－250型苎麻剥麻机结构属性，本文基于ANSYS Workbench 软件，采用计算机有限元方法对剥麻机的机架进行模态分析。

将简化后的剥麻机机架模型以igs 文件形式导入至ANSYS Workbench 中，对其进行材料属性的定义:剥麻机机架所用材料为结构钢，弹性模量为2.06×105N/mm2，泊松比为0.30，密度为7.85×10－6kg/mm3。将剥麻机机架各梁之间定义为自动接触类型。采用四面体tetrahedrons 网络对模型进行网络划分，网络控制采用size ＝4 mm。计算机架的前12 阶模态，采用program controlled 求解器进行计算。机架的7～12 阶模态云图如图4所示，频率分布图如图5所示。机架前12 阶振动频率及其振动特征如表3所示。

表3 机架前12 阶振动频率及其振动特征Table 3 The first 12 vibration frequencies and vibration characteristics of the frame

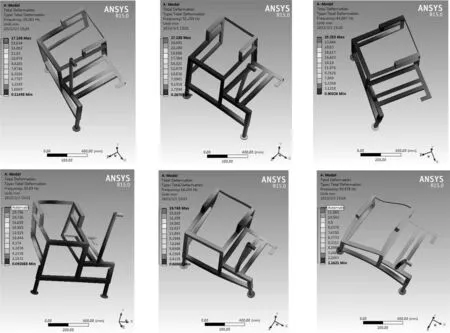
图4 7～12 阶模态云图Fig.4 7－12 order modal cloud map

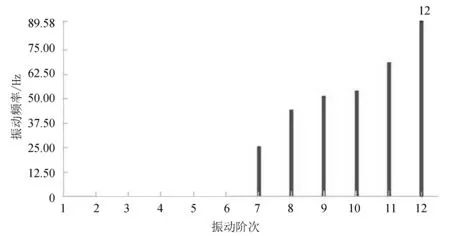
图5 机架的前12 阶固有频率分布Fig.5 The distribution of the first 12 natural frequencies of the frame

由图5 可知，机架的前1～6 阶模态的振动频率为0，这是其自由状态下的刚体模态，符合分析实际情况。由振动理论可知，结构的振动可以表达为各阶固有阵型的线型组合，其中低阶的振型对结构振动特性的影响远高于高阶振型。因此，低阶振型决定了结构的动态特性，故提取7～12 阶次的模态进行分析。第7 阶模态的振动频率为25.28 Hz，最大变形位移为17.19 mm，频率的振动特性为沿x轴扭转振型，同时沿z轴扭转，最大变形处为两个支撑脚和收集杆处，分析原因可能是机架下横梁与机架的纵梁之间存在高度差，且缺乏斜支撑连接；第8 阶模态的振动频率为44.09 Hz，最大变形位移为25.26 mm；第9 阶模态的频率为51.26 Hz，最大变形位移为27.13 mm；第10 阶模态的频率为53.69 Hz，最大变形位移为22.87 mm，最大变形处都集中在接麻秆的最上端。第8～10 阶频率比较接近，主要阵型为沿x轴扭转振型，沿z轴扭转及弯曲变形，分析原因可能是机架出麻口位置的左、右两侧部分下方未连接横梁，这是机器结构设计中排放麻渣的需要，可以考虑将连接左右两侧机架的上梁由扁钢改为方钢或角钢。第11 阶模态的频率为68.28 Hz，最大变形位移为19.76 mm。第12 阶模态的频率为89.58 Hz，最大变形位移为12.63 mm，主要阵型为沿X轴弯曲。

机架的固有频率与激励频率满足式(7)时不会发生共振[11－12]。

式中:ω0－固有频率，Hz；ω－激励频率，Hz。

由于机架承载的主要外部激励源部件为剥麻滚筒和柴油机组，其运动形式主要为旋转运动。工作时，剥麻滚筒的转速为800 r/min，柴油机内部转子的转速为2600 r/min。根据圆周运动频率与转速的关系式(8):

式中:f－匀速圆周运动的频率，Hz；n－转速，r/min。

故剥麻滚筒和柴油机组的频率分别为13.33、43.33 Hz。柴油机转子的运动频率与机架的第8阶固有频率在同一区间范围。因此，机架在工作时有可能与外部激励产生共振。对照第8 阶频率的振动类型及变形特点，针对性加强机架出麻口位置左、右两侧部分的连接作用。

3.3 机架结构优化

针对上述模态分析结果，对结构模型进行优化，将机架左侧部分出麻口位置的连接横梁，由原来的40 mm 扁钢改为40 mm 角钢，模型的其他部分不做改变。再次对改进优化后的模型进行模态分析。分析结果表明:机架的前1～6 阶模态的振动频率为0，第7～12 阶模态的频率分别为17.92、35.56、44.56、53.94、57.41、70.25 Hz。对比改进前，改进后模型的各模态频率均有所下降，平均下降15.81%，且各阶模态下的变形均较小。经比对，该模型的第9 阶模态频率与发动机的运动频率在同一区间范围，第9 阶模态云图如图6所示，在该模态下样机整体的变形较小，最大变形量为24.92 mm，发生在竖直晾麻杆的位置，此位置的变形不影响剥麻机的整体性能，且该晾麻杆可以互换更替。其余变形均在10 mm 以下，相比较改进前的结构，该结构明显更优。

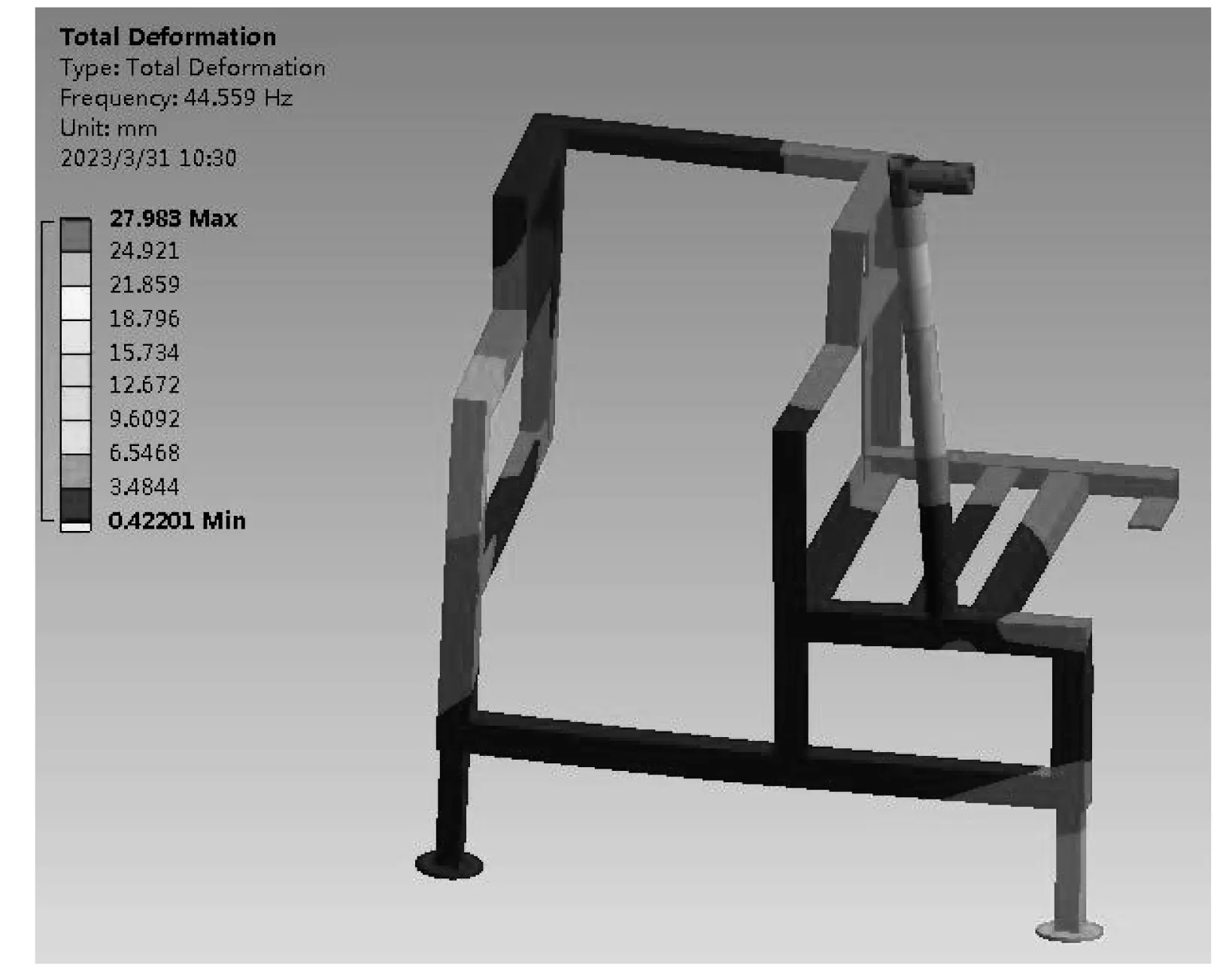
图6 改进后机架第9 阶模态云图Fig.6 Improved 9th order modal cloud map of the frame

4 结论

(1)机架的静力学分析表明:机架在加载后所受到的应力为23.71 Mpa，低于材料的屈服强度156.67 Mpa。因此机架结构在条件载荷下的强度和刚度满足设计要求。

(2)机架的模态分析表明:机架的前1～6 阶模态的振动频率为0，7～12 阶模态的频率为25.28～89.58 Hz。剥麻滚筒和柴油机组的频率分别为13.33、43.33 Hz。柴油机转子的运动频率与机架的第8 阶固有频率在同一区间范围。因此，机架在工作时有可能与外部激励产生共振。对照第8 阶频率的振动类型及变形特点，针对性加强机架左侧部分出麻口位置左、右两侧部分的连接作用。

(3)针对上述分析结果对结构模型进行优化，并对改进优化后的模型再次进行模态分析。结果表明:机架的前1～6 阶模态的振动频率为0，第7～12 阶模态的频率分别为17.92、35.56、44.56、53.94、57.41、70.25 Hz。对比改进前，改进后模型的各模态频率均有所下降，平均下降15.81%，且各阶模态下的变形均较小，主要部件的变形量均在10 mm 以下，改进后的结构综合力学性能有明显提升。