偏振导航云计算支持系统与时空分布规律模型研究
张羽,汲万峰,隋江波,杭伟,陈瑞
( 1. 中航贵州飞机有限责任公司, 贵州 安顺 561018;2. 海军航空大学航空基础学院, 山东 烟台 264001;3. 桂林航天工业学院, 广西 桂林 541004;4. Department of Computer Science, Tufts University, Medford, MA, USA 02155 )
0 引言
研究表明,在某天的某一时刻、某一位置,天空中具有相对稳定的偏振模式图[1-3],天空偏振模式图具有两条对称线:一条是与太阳角距为90°的最大偏振线;另一条是经过太阳和天顶的太阳子午线. 许多生物就是通过自身敏感偏振的视觉系统感知天空偏振模式图的对称线——太阳子午线,并以此为依据确定身体长轴与太阳子午线之间的夹角[4-8]. 一方面,通过测量同一时刻不同地理位置观测到的天空偏振光分布情况,可以看出同一时刻不同位置观测到的天空偏振光分布是有差异的[9-12],那么在实际使用过程中多大的区域内可以认为天空偏振光分布是一致的. 也就是说,在多大的区域内由偏振光分布差异造成的误差在系统允许的误差范围之内;另一方面,通过连续观测天空偏振光分布情况,可以看出天空偏振光分布随着时间的变化而变化,那么在以上确定的区域内多长时间可以认为天空偏振光分布是不变的. 也就是说,在以上确定的区域内多长时间采样一次偏振光分布可以忽略由时间变化带来的误差. 为了使仿生偏振导航系统在实际现场高精度自动运行,本文采取多单体、长时间反复操作的“测量-计算-搜寻-分析-描述-提高”研究方案对信息源时间域、空间域误差模型以及特定的时间域、空间域内载体测量误差进行分析,并对抑制误差的信息处理算法进行研究.
1 仿生偏振导航误差分析及多导航单元云计算支持系统
针对仿生偏振导航,不少学者设计了偏振光导航测角平台,可以测量解算当前方向与太阳子午线之间的夹角. 载体的测量误差主要由随机误差以及载体固有的系统误差组成,消除载体的随机误差并提取系统误差是提高测角精度的重要因素[13-18].
以偏振导航10 m 精度为例,信息源误差的贡献率不超过10%(小于1 m)为实际使用. 信息源的误差主要是天空偏振模式图随时间、空间的变化造成的,本课题首先研究在多大的区域天空偏振模式图的变化引起信息源的误差在1 m 范围内,在确定的范围内,多长的时间间隔内天空偏振模式图的变化引起信息源误差在1 m 的范围内. 研究思路,首先是将100 个同方向的样本放在一个小区域里,计算同一时刻100 个样本的统计学误差,如果小于1 m,扩大区域并计算误差,直至达到允许的最大信息源误差,这样就确定了不变的空间区域A. 然后将10 个同方向的样本放在上述确定的区域,以不同的时间间隔采样信息计算误差,直至找到误差允许范围内的时间间隔,这样就确定了特定空间区域内的采样间隔T. 这部分研究内容可以为偏振导航的实际使用提供参考依据.
测量误差是载体的主要误差,在确定的区域、确定的时间间隔内信息源误差可视为常数,载体测量误差的变化和提取方式的研究思路首先是将100 个同方向的样本放在特定的区域A内,在确定的时间间隔T内多次采样信息并通过Kalman 滤波消除单体随机误差,这样就可以得到含系统误差的测量值;其次将100 个同方向的样本放在上述确定的区域,同时采集100 个样本的测量值,因为各样本的系统误差是不相关的,通过Kalman 滤波即可得到消除了测量误差的准真值;最后对仿生偏振导航数学模型进行仿真,将仿真结果与准真值比较即可得到各单体的系统误差,这部分内容可以作为今后使用过程中修正系统误差的基本依据.
上述实验涉及到100 个单体测量系统、10000 个采样时刻、100 次重复性测量与计算以及改进型Kalman 滤波的递推运算,提取信息源误差和载体测量误差都涉及到时间和空间的问题,地理范围与采样间隔的持续变化,使得中间的运算量巨大;而各单体本身要用到Kalman 滤波消除随机误差,多单体需同时进行时域、空域搜寻的评估计算和结果参数的统计学计算. 这些问题相互关联,计算复杂,同时并行或串行地运用在多个单体和多次重复性实验中. 各种计算拥有大量相同的结构和模型,因此可以充分利用计算单元阵列的可重组和可并发特点进行任务划分提高计算效率. 上述基于多单体滤波的误差分析计算阵列结构具有强大的冗余容错能力,可忽略某个单元的计算错误甚至信息丢失,随时可以进行系统重构,保证了计算的实时和有效. 在这样一种接近云计算结构的多单元、多进程计算阵列体系下,采用云计算技术及并行算法,通过变化的多导航单元网络联合解算显得非常必要如图1~2 所示,通过对单体仿生偏振导航进行误差分析、使用云计算技术辅助多导航单元系统进行高速运算,可以提高仿生偏振导航的精度及实用性.
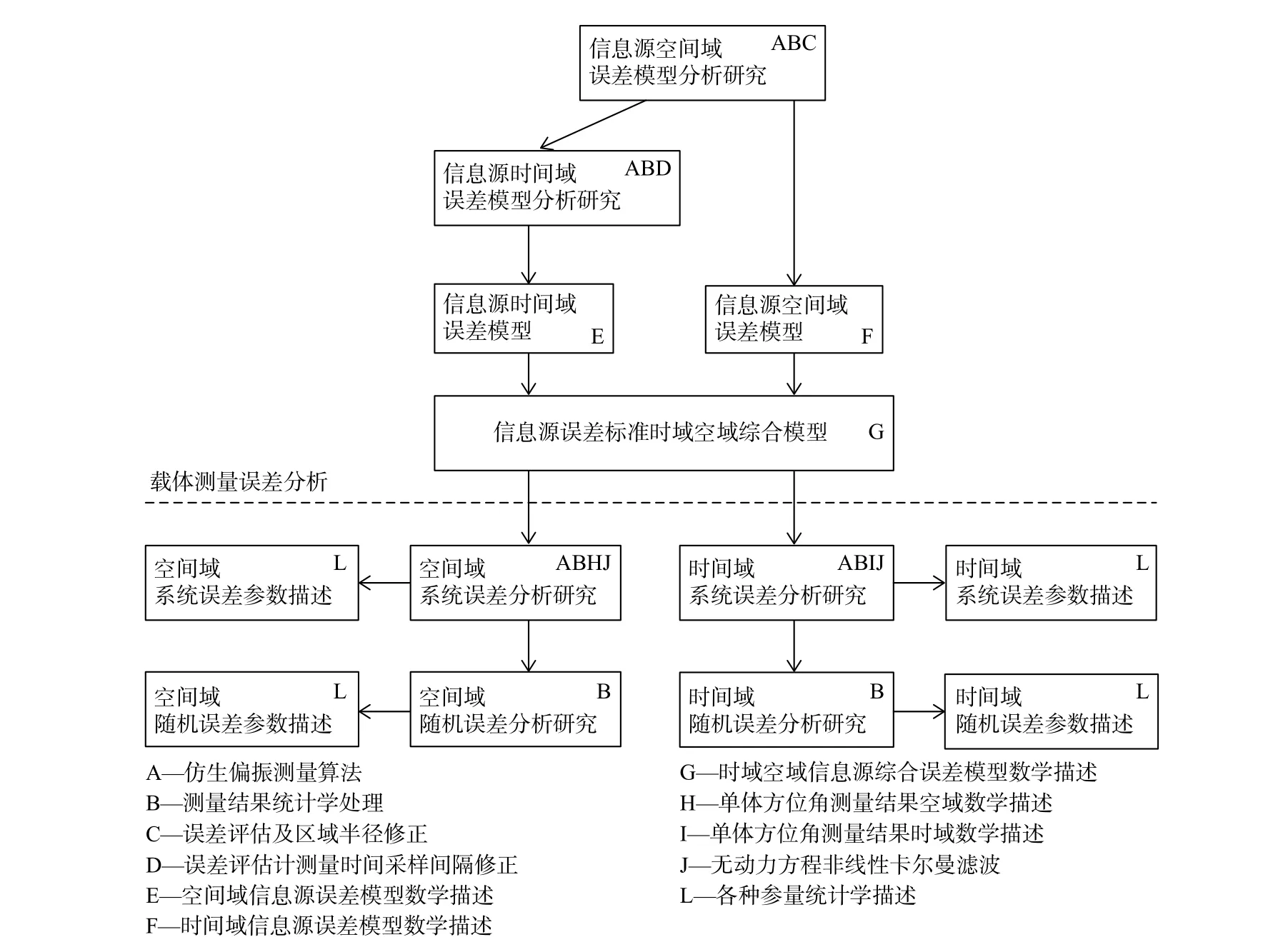
图1 信息源误差与测量误差的时域、空域模型建立
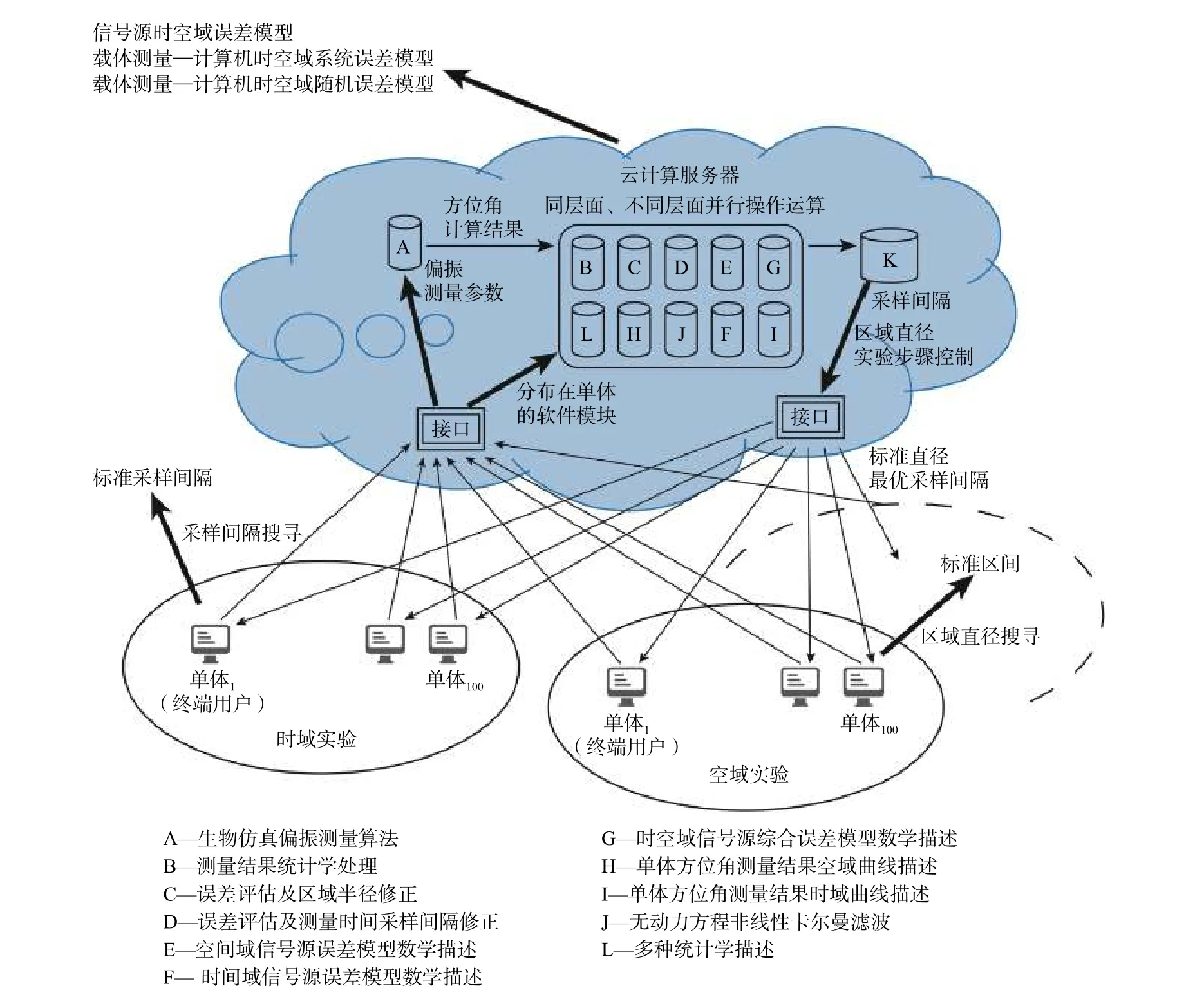
图2 信息源误差与测量误差模型分析的云计算支持系统
如图3 所示,系统主要包括天空偏振光分布模型及其特性分析;仿生偏振导航的实现及单体导航误差分析;多导航单元云计算支持系统的提出及并行算法分析;信息源时间、空间域分辨率模型的建立;时间、空间域测量系统随机误差、系统误差分析与模型建立以及云计算支持系统条件下的仿生偏振导航整体运算过程中的并行算法[19].
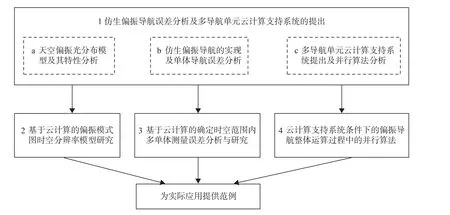
图3 云计算支持技术框图
1)仿生偏振导航误差分析及多导航单元云计算支持系统的提出利用全天空偏振测量方法分析天空偏振模式图随载体时间、位置变化的关系,并对前期设计的偏振导航测角平台误差进行分析,提出采用云计算及并行算法提高偏振导航的精度. 具体包括天空偏振光分布模型及其时间空间特性分析、仿生偏振导航的实现及单体导航误差分析、多导航单元云计算支持系统的提出及并行算法分析.
2)基于云计算的偏振模式图时空分辨率模型研究划分出给定精度内不同测量位置(或时刻)得到相同偏振光模式图结果的区间(或时段)范围,目标是基于多导航体的云计算方法,建立不同精度下偏振模式图通用区间和通用时段模型. 具体包括信息源空域误差模型的建立、信息源时域误差模型的建立.
3)基于云计算的确定时空范围内多单体测量误差模型研究建立相同偏振模式图下针对时域和地域变化的多单体导航测量序列最优估计算法——时域、地域Kalman 滤波递推算法,分析确定时空范围内多单体偏振导航的测量偏差及其偏差抑制模型. 具体包括空域测量系统随机误差、空域系统误差分析与模型建立、时域测量系统随机误差、时域系统误差分析与模型建立.
4)云计算支持系统条件下仿生偏振导航整体运算过程中的并行算法为偏振模式图的时空分辨率模型研究和多单体导航误差模型研究提供具体的运算手段. 具体包括信息源空间域误差分析模型的并行计算结构设计、信息源时间域误差分析模型的并行计算结构设计、确定空间域内载体测量误差分析的并行算法、确定时间域内载体测量误差分析的并行算法和多单体Kalman滤波与量测估计的并行计算.
2 基于云计算的偏振模式图时空分辨率模型研究
为提高基于云计算的现场自动运行仿生偏振导航测量的精确度,首先需要建立普遍适用的信息源的空间域、时间域误差模型. 下面以100 个单体组成的群体运动、10 个单体组成的单体运动、1 m 距离的天球信息源系统允许误差(即10 m 的地球表面方位距离误差)为例分别描述空间域、时间域误差模型的建立过程. 载体的测量误差主要由噪声、热效应等引起的随机误差以及机械结构等原因引起的系统误差造成的,这部分内容就是在确认的时空范围内对多单体时域、空域随机误差、系统误差进行分析并建立模型.
2.1 信息源空域误差模型的建立
如图4 所示,对待测区域内100 个单体进行方位角等效长度测试,求其统计平均误差后进行评估并调整区域直径,直至到达误差容忍临界值为止,由此确定信息源空间域误差容忍区直径[18].
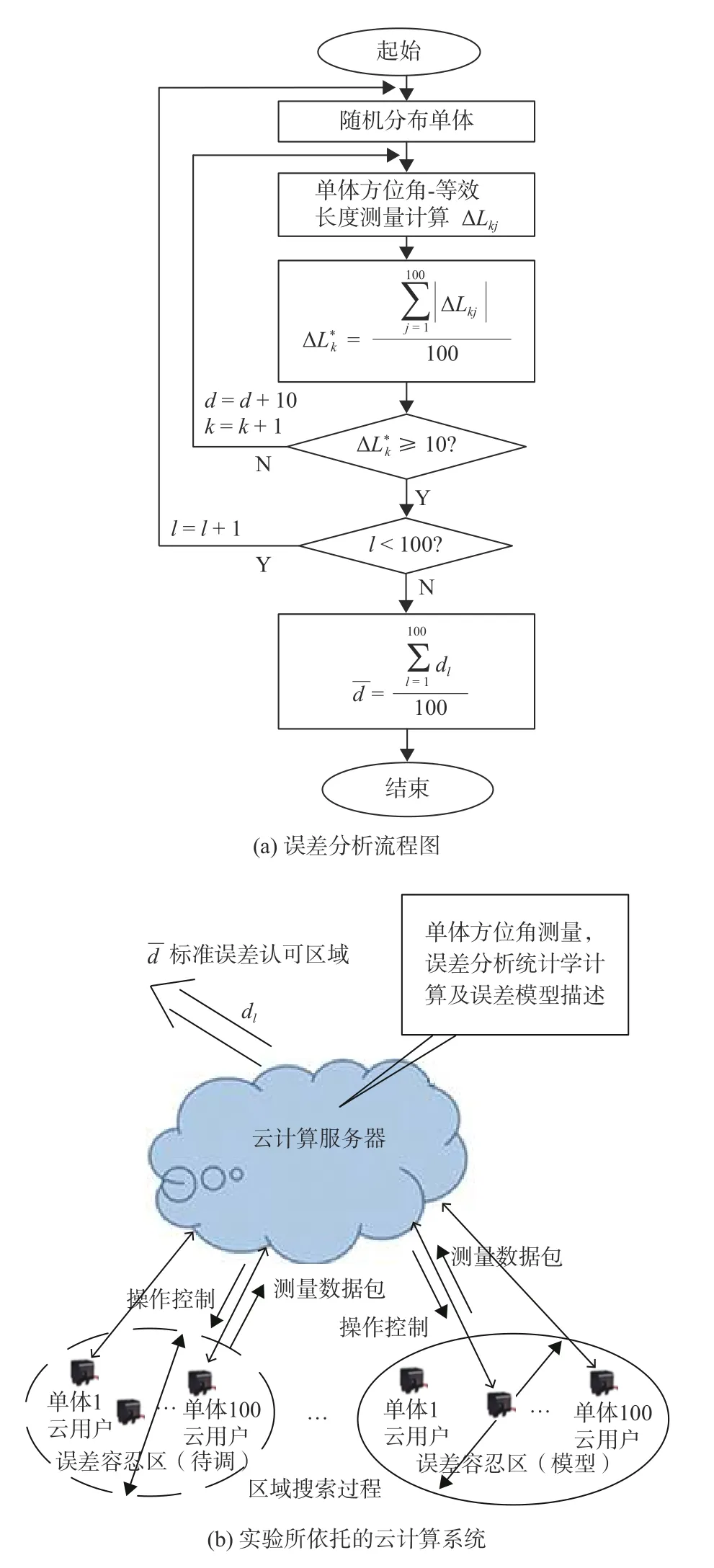
图4 信息源空域误差分析实验
步骤1:随机分布单体,在直径为dM(d从100 开始,以10 为步长逐次增大)的圆面上随机分布(充满圆面)100 个运动单体且令其在实验过程中方向相同、静止不动.
步骤2:单体方位角测量计算,令各单体同时进行一次单体方位角测量计算(相同的天空模式图). 设其测量结果分别为方位角α、k、j,k=1,2,···,j=1,2,···,100(k为实验次数,j为单体号).
步骤3:统计学误差计算,计算所有单体方位角与所有单体方位角平均值之差,将其折算为等效地理距离,记作ΔLk,j,单位为m,并计算均方根误差(root mean squared error,RMSE)
步骤4:评估并调整d,评估区域直径d:若ΔLk<10,则增大d一个步长,并令k=k+1.
步骤5:重复调整d,重复步骤1~4,直至达到ΔLk≥10 为止,记下前一次的区域直径dl,l=1,2,···为实验次数.
步骤6:重复实验,令l=l+1,重复步骤1~5(每次实验的第一步,都将上述100 个单体作重新的随机分布),直至得到dl,l=1,2,···,100.
2.2 信息源时域误差模型的建立
如图5 所示,对上述标准误差容忍区域内的10 个单体进行方位角等效长度统计误差平均值进行评估,直至误差到达容忍临界值为止,从而确定满足信号源误差容忍范围的最佳测量采样间隔.
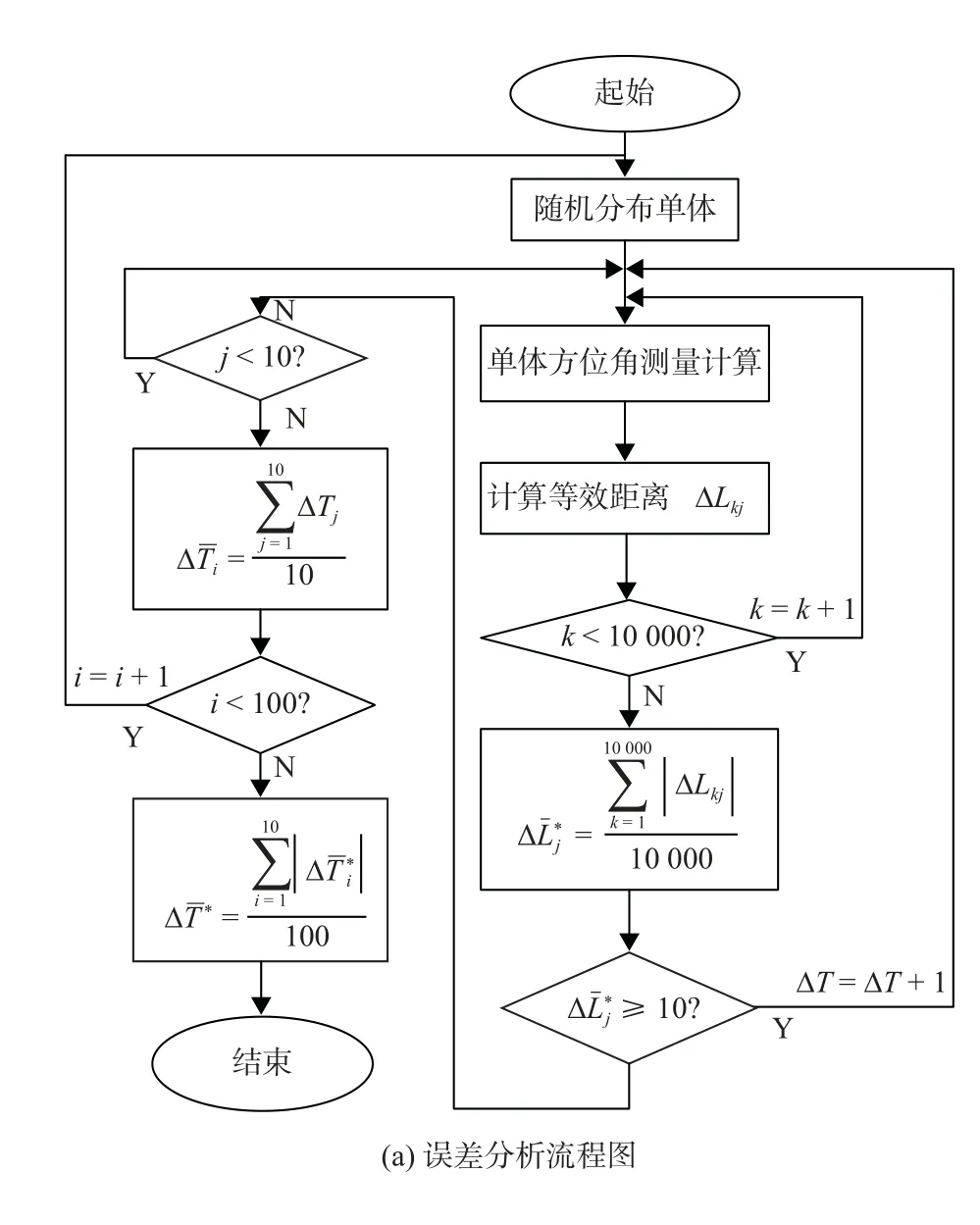
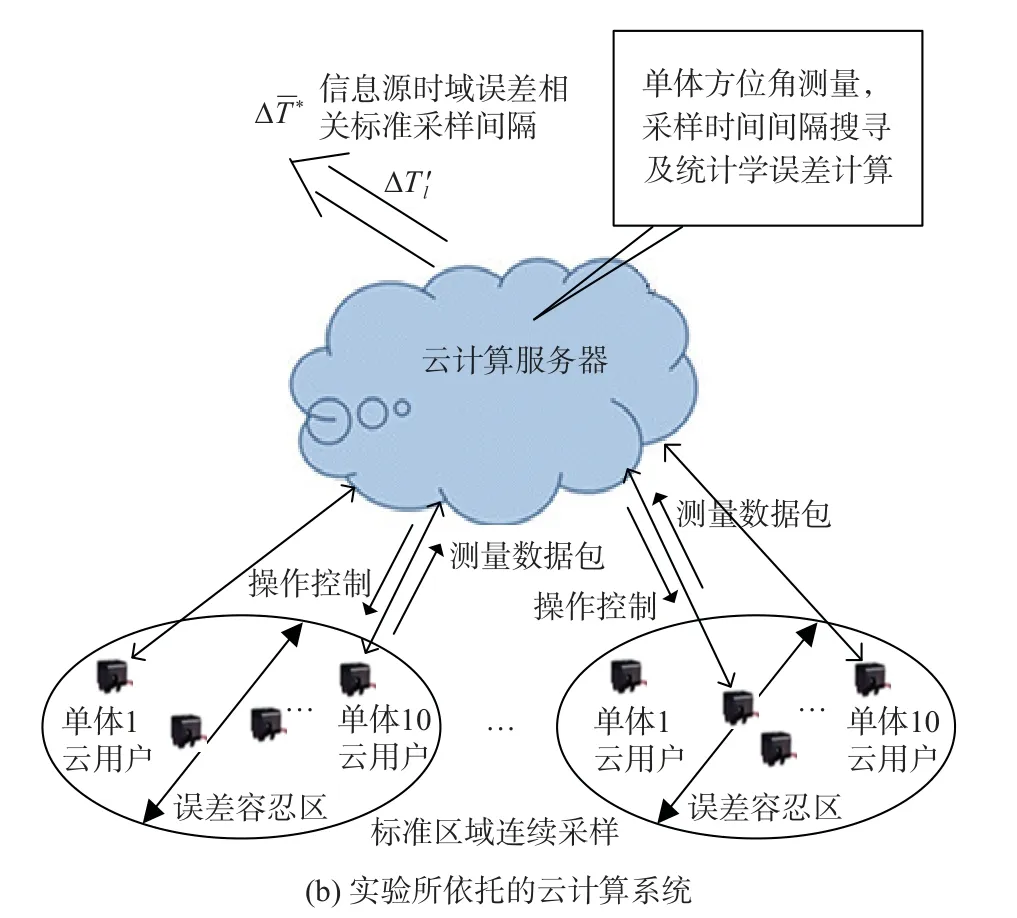
图5 信息源时域误差分析实验
步骤1:单体分布,在上述实验确定的区域dl内随机分布10 个运动单体(充满整个区域).
步骤2:单体方位角测量计算,在相隔时间为ΔTl的时刻Tk,k=1,2,···,10000,令所有单体同时执行单体方位角测量计算,得到10000 组、每组10 个单体的方位角{αk,j},k=1,2,···,10000,j=1,2,···,10.
步骤3:统计学误差计算,计算上述所得所有单体统计学误差,并将其折算为等效地理距离,记作ΔLk,j,单位为m,并计算统计学误差j=1,2,···,10.
步骤4:评估ΔT,若有ΔL*<10,则将ΔT增加1 h,重复步骤2~3,直至第一次出现ΔL*≥10,记下前一时刻的采样时间间隔 ΔT′,并求平均值,l为实验次数.
步骤6:统计学平均采样间隔计算计算上述100 次实验的统计学结果(i为实验次数):ΔT¯*=,ΔT*即为系统所求采样间隔.
3 基于云计算的确定时空范围内多单体测量误差分析与研究
载体的测量误差主要由噪声、热效应等引起的随机误差以及机械结构等原因引起的系统误差造成的,本节在上述实验确认的时空范围内对多单体时域、空域随机误差、系统误差进行分析并建立模型.
3.1 空域测量系统随机误差、系统误差分析与模型建立
如图6 所示,采用信息源误差模型所规定的采样间隔和区域直径,对多个单体同一时刻进行方位角测量,求其等效长度误差,统计平均值,并通过改进的Kalman 滤波和统计学计算,对误差的系统性和随机性进行分析和最终的模型描述.
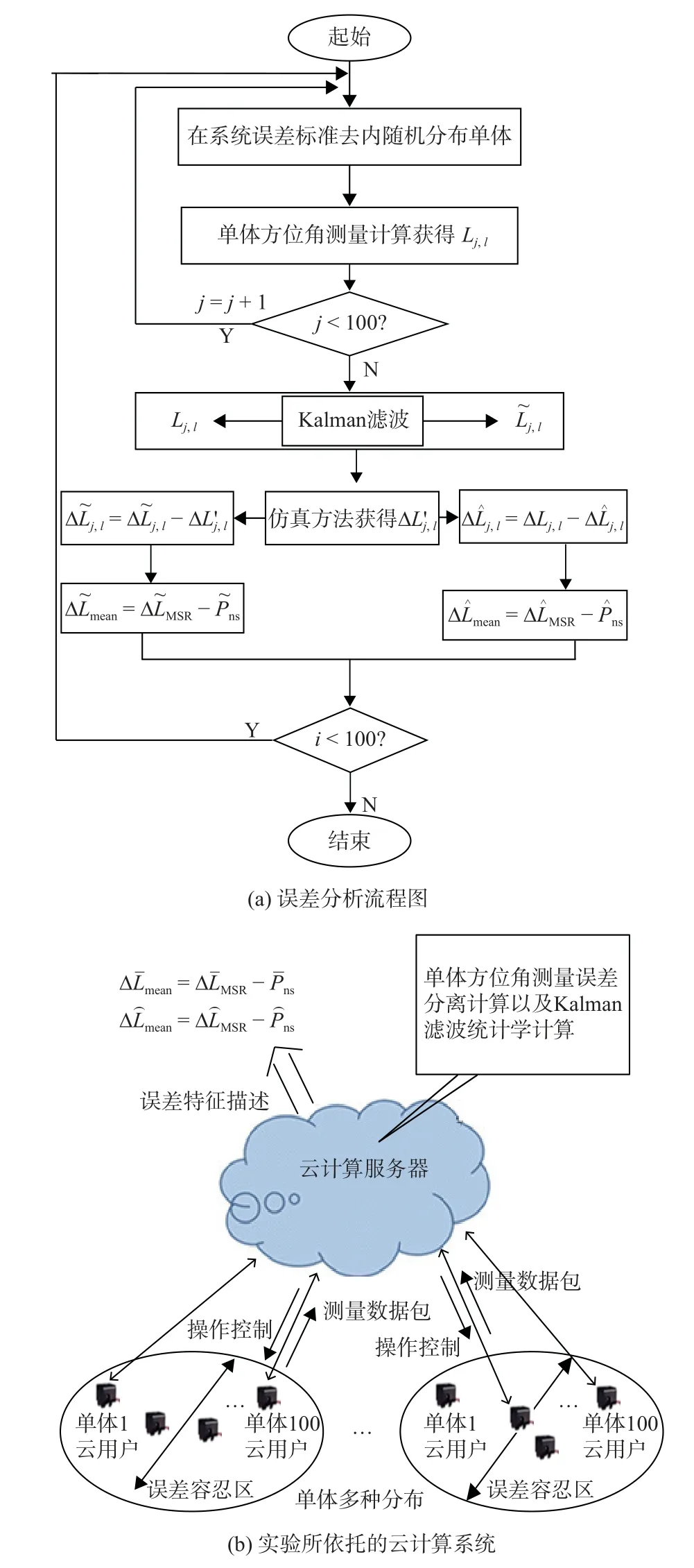
图6 空域系统测量误差分析实验
步骤1:随机分布单体,在直径为dM(在2.2.2 节中获得)的圆面上随机分布(充满圆面)100 个运动单体且令其在实验过程中方向相同、静止不动.
步骤2:单体方位角测量计算,令圆面内各单体在某一时刻同时进行一次方位角测量计算,并将测量结果转换为地理长度Lj,l,单体序号j=1,2,···,100,实验次数l=1,2,···,100. 每次实验得到一条地理长度曲线(观测值曲线)Lj,l,j=1,2,···,100.
步骤3:单体方位角高精度值测量计算,采用仿真方法得到上述单体的高精度方位角等效长度准真值曲线Lj,l,j=1,2,···,100.
步骤4:单体方位角等效长度空间域系统误差的分离,设计适合于本实验所面对的测量条件与环境的无动力方程非线性Kalman 滤波算法,并将其作用于Lj,l,j=1,2,···,100,从而得到随机误差足够小而系统误差占主导地位的测量结果(估计值曲线),记作(j=1,2,···,100). 在此基础上计算出准系统误差曲线并计算此误差的最大值、平均值和均方根分别为[20]:和.
步骤5:重复计算系统误差描述参数统计平均值,令l=l+1,重复步骤1~4(每次实验的第一步,都将上述100 个单体作重新的随机分布),直至l=100,从而获得上述各参量的平均值. 以这些参数为评判标准,可以进行仪器和环境的系统误差来源分析,从而为抑制测量计算系统误差提供依据.
步骤6:单体方位角等效长度空间域随机误差的分离,计算出准随机误差曲线2,···,100,并计算此误差的最大值、平均值值和均方根分别为:ΔLmax=max(ΔLj,l).
步骤7:重复计算求随机误差描述参数统计平均值,令l=l+1,重复步骤1~4(每次实验的第一步,都将上述10 个单体作重新的随机分布),直至l=100,从而获得上述各参量的平均值. 以这些参数为评判标准,可以进行仪器和环境的随机误差来源分析,从而为抑制测量计算提供评估依据.
3.2 时域测量系统随机误差、系统误差分析与模型建立
如图7 所示,采用信息源误差模型所规定的采样间隔和区域半径对区域内多个单体进行长时间方位角测量、并采用改进的Kalman 滤波和统计学计算进行系统误差和随机误差的分析与模型描述.
图7 时域系统测量误差分析实验
步骤1:随机分布单体,在上述实验确定的标准误差容忍区内随机分布100 个运动单体(充满整个区域).
步骤2:单体方位角测量计算,在上述所获得的时间间隔ΔT*内的时刻Tk,k=1,2,···,10000 中,对所有单体同时执行单体方位角测量计算,得到10000组、每组100 个单体的方位角等效长度观测值曲线Lk,j,l单体序号j=1,2,···,100、实验序号l=1,2,···,10000.
步骤3:单体方位角高精度值测量计算,对k时刻获得的100 个单体的等效长度Lk,j,l,j=1,2,···,100,进行空间Kalman 滤波,获得随位置(即随单体序号)变化的等效长度估计值曲线Lk,j,l. 由于任一时间序列Lk,j,l,k=1,2,···,100 与任一空间序列Lk,j,l=1,2,···,100 不相关,因此,Lk,j,l可认为是Lk,j,l在k时刻的准真值,而在下面的试验中特将其作为近似的真值来使用.
步骤4:单体方位角等效长度时域系统误差的分离,设计适合于本实验所面对的测量条件与环境的无动力方程非线性Kalman 滤波算法,并将其作用于Lk,j,l,k=1,2,···,10000,从而得到随机误差足够小而系统误差占主导地位的测量结果,估计值曲线L统误差为主要误差的单体方位角等效长度准系统误差曲线j=1,2,···,100. 在此基础上计算出以系统误差为主要误差的单体方位角等效长度准系统误差曲线,并计算此误差的最大值、均值和均方根分别为和
步骤5:重复计算求系统误差描述参数统计平均,令l=l+1,重复步骤1~4(每次实验的第一步,都将上述100 个单体作重新的随机分布),直至l=100,从而获得上述各参量的平均值. 以这些参数为评判标准,可以进行仪器和环境的系统误差来源分析,从而为抑制测量计算系统误差提供依据.
步骤6:单体方位角等效长度时域随机误差的分离,计算出以随机误差为主的测量准随机误差曲线,k=1,2,···,10000,j=1,2,···,100.并计算此误差的最大值、均值和均方根.
步骤7:重复计算求时域随机误差描述参数统计平均,令l=l+1,重复步骤1~4(每次实验的第一步,都将上述100 个单体作重新的随机分布),直至l=100,从而获得上述个参量的平均值. 以这些参数为评判标准,可以进行仪器和环境的随机误差来源分析,从而为抑制测量计算提供评估依据.
4 小 结
本文根据天空偏振模式图随载体时间、位置变化的关系及偏振导航的特点,提出了采用云计算提高偏振导航的精度,设计了多导航单元云计算支持系统的结构框架;针对基于云计算的偏振模式图时空分辨率模型进行研究,划分出给定精度内不同测量位置(或时刻)得到相同偏振光模式图结果的区间(或时段)范围,目标是基于多导航体的云计算方法,建立不同精度下偏振模式图通用区间和通用时段模型;针对基于云计算的确定时空范围内多单体测量误差模型进行研究,建立相同偏振模式图下针对时域和地域变化的多单体导航测量序列最优估计算法—时域、地域Kalamn 滤波递推算法,分析确定时空范围内多单体偏振导航的测量偏差及其偏差抑制模型,建立了空域测量系统随机误差和系统误差模型、时域测量系统随机误差和系统误差模型. 采用云计算技术解决天空偏振模式图受环境影响导致的信息源误差以及载体自身测量产生的误差可以有效提高仿生偏振导航的精度及实用性. 本文针对偏振导航云计算这一新领域问题开展研究,旨在通过总体性的论述、研究思路与理论方法介绍,介绍导航“偏振场”及作者团队开展的技术方法研究. 文中针对偏振导航云计算问题提出研究思路,研究系统模型,进行误差分析,目的是完善自然场导航专刊的研究框架,下一步将针对所提方法开展实验验证研究,以提供数据的支撑.

