地形导航多波束测深综合效应的邻域改正技术
于家成,姜凯文,赵红颖
( 1. 华北科技学院电子信息工程学院, 河北 廊坊 065201;2. 北京大学遥感与地理信息系统研究所, 北京 100871 )
0 引言
多波束声纳测深系统,又称为多波束条带测深仪,是一种由回声测深设备和处理设备组成的复杂系统[1]. 与传统的单波束测深仪相比,可以获得与航向垂直的垂面内的全覆盖水深观测条带,一个条带覆盖区域内多个测量点的海底深度数据[2],同时具有扫幅较宽、测点密度较高的特点;较窄的波束、先进的检测技术和精密的声线改正方法的采用,也确保了测点船体坐标的归位计算精度,从而能够精确、快速地测出沿航线一定宽度内水下目标的大小、形状和高低变化,同时兼顾了海底地貌的描绘,极大地提高了测量效率,获得的数据基于不同目的可以运行不同的软件,得到海底地形不同方面的特性,这既减少测量船勘测设备购置成本,也提高了测量设备的用途,节省能源和空间,实现了海底多种特性的共点同步探测[3].
在多波束系统水下测量时,其作业模式多采用无验潮测量技术,利用外业测量和内业修正相结合的方式. 由于测量环境的特殊性,影响测量的因素很多,从而降低测量质量,误差来源包括卫星影响、地形起伏、公式计算误差多路径效应、伪值等. 水温、盐度、水质密度也对声速产生影响,测量结果结合定位技术同步进行[4-5]. 形成的海图既能用于地形匹配导航,也兼具测量海底的沉积物分布[6].
在海底地形测量过程中,由于波束存在宽度,尤其波束具有宽度和地形起伏之间的相互作用,以及测船的摇摆等因素都对测量效果产生影响,这种效应通常称为波束角效应和地形效应. 这种波束角效应,是由于测深仪换能器自身发射波束存在一定开角,在测深过程中,换能器记录的数据是最早接收到的声信号,并以此作为计算水深的依据,因此换能器记录的水深值可能是水底波束覆盖区域内任意一点至换能器的最短距离[7-8]. 该效应普遍存在于水下地形测量中,在地形起伏变化复杂的区域更为明显,目前一些国家的海道测量规范中已将此项测深误差的处理列为必要步骤. 所谓地形效应,是由于测船在行驶过程中,测量范围内的地形时刻都在变化,而换能器接收到的回声是波束内所覆盖的地形的最近距离,会使得测深变浅. 同时,由于海浪冲击引起测船颠簸,使得测船倾斜,导致波束向海底的入射角发生改变[9]. 文献[9-11]使用了单波束系统基于一维及三维测线,对波束角的宽度和地形影响进行了分析与改正;文献[12]对多波束系统水深测量中的地势效应进行分析,使用地形模板的方式进行了改正.
本文认为由于波束角的存在和地势的起伏,测量回波获得的是波束投射区域的最近距离,从而具有测量误差,测量过程中需要根据不同测点地势通过测线两侧的水深值对扫描形成的测量条带进行改正. 文中设计多波束数字测深模型,对多波束扫描过程中形成的测深条带进行了仿真验证,综合分析了波束宽度和地形起伏对水深测量的影响,进而对测深数据进行了改正.
1 多波束系统水深测量模型
在进行多波束系统扫描仿真时,若忽略发射阵沿船体纵向的波束宽度,只考虑沿船横向的波束平面开角 θ ,则建立如下测深模型.
1.1 模型设计
如图1 所示,设载体纵向为X轴,船艏为正向,横向为Y轴,垂直向下为Z轴,按右手直角法则建立测量坐标系,载体沿X轴正向航行,根据文献[13],对原始水深数据进行样条插值模拟实际地形图,实际已知的水深资料是按照经度方向和纬度方向进行近似等间距采样的矩形网格点水深数据,经过更密集的插值后,在经度和纬度方向上形成更细微的矩形网格点,用以模拟真实二维海底离散水深值z(xn,ym) ,n,m=1,2,···,N.
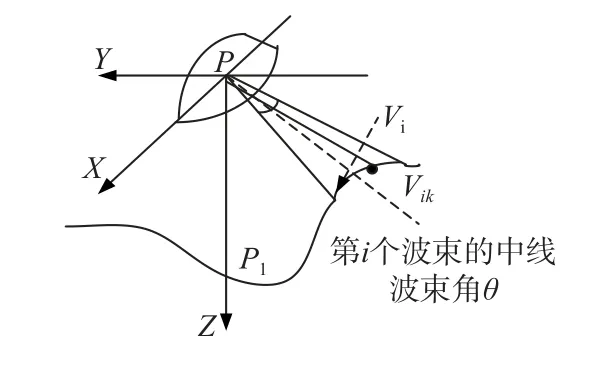
图1 载体侧面波束测量海底水深示意图
设当前船载多波束声纳系统换能器发射接收阵位置为P(xn,ym,0),n,m=1,2,···,N,其在海底面的投影为P1(xn,ym,z(xn,ym)),n,m=1,2,···,N,波束发散角为 θ ,波束数为 2M,沿船体左右舷对称布设,图1 仅展示了左舷部分,右舷部分对称.
设船体沿纬线直线航行,以船体纵向为对称中线,左舷第i个波束投射的海底离散点形成一个离散点集Vi,i=1,2,···,M.
忽略盐度、水温、水质密度等因素的影响,则第i个波束从换能器到测点的声线测量距离为
其中,D(xn,ξl,z(xn,ξl))=.
则第i个波束的换能器下水深换算值为
距离中心点的水平距离为
式中:Yi表示该波束所产生的脚印位置;为波束的入射角.
船体右舷波束与船体沿经线直线航行时分析类似.
1.2 扫描设计
1) 离散点搜索
对原始测深数据进行精密插值,形成DTM. 尽量使一个波束覆盖至少一个网格,以保证在一个波束内能够测量到至少一个网格点处的水深值.
2) 依左舷建立第一个波束投射点搜索区间
3) 相邻波束测点之间的填补
将所有波束测量点的水深数据归结到最近网格点后,再将其他网格点的水深值用前一个所归结网格点的水深值进行代替.
1.3 以邻域测点改正中心测点
1.3.1 测量中真实水深与记录水深的关系
在多波束测深过程中,存在波束宽度及地形起伏,这些因素都对测深产生影响[14]. 由于波束的立体特性[15],投射海底的面为一微小近似圆面,如图2所示.
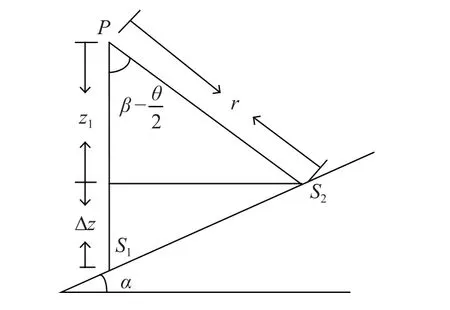
图2 载体侧面波束测量海底水深示意图
设换能器位于P点,将得到换能器到该圆面的最小距离r作为测量记录距离,经过分析,真实水深为
式中: β 为波束入射角; θ /2 为半波束角; α 为海底倾斜角.
其中, β 可以根据载体的俯仰角、横绕及侧面波束数目计算获得, θ/2 为已知量,在测量过程中地形是未知的,但可以根据测量记录水深值估计 α .
如图3 所示,设有3 条测线,参考图的中间点,通过两侧的测深值对测深中点进行水深改正,在每个测点周围沿8 个方向计算其平均坡度=1/8作为该点处坡度的估计,h为水深换算值,用作为该点处倾斜角的估计.
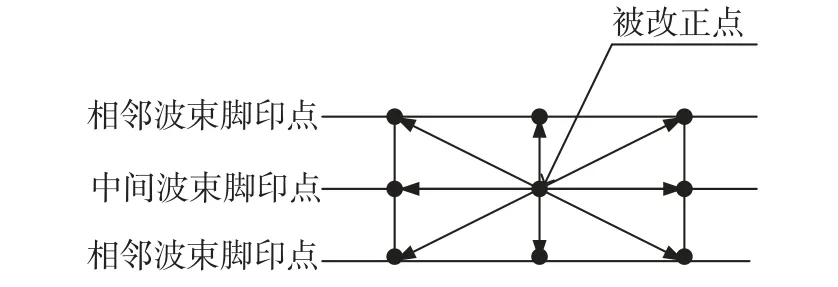
图3 载体侧面波束测量海底水深示意图
1.3.2 平均测深差和平均改正量
改正前平均测深差: 设有N个实际水深值x(1),x(2),···,x(N),其相应测量记录值为r(1),r(2),···,r(N),则其平均测深误差为
式中,D为测量值与实际值之间的偏离程度.
平均改正量:设经过改正后,水深值为x′(1),x′(2),···,x′(N),则其平均改正量为
该量用以表达对测量值的改正程度.
改正后的平均测深差:以改正后的水深值与真实水深值之间的差作为平均测深差
2 实验仿真
仿真中应用本文设计的多波束数字测深模型设波束角2°,共有16 条波束,在纬度25.6317 处沿纬度方向设置测线路径,从起始经度125.1281 到终点经度125.1285 采样10 个点,中间波束的水深如图4 所示,沿途区域真实水深如图5 所示为一马鞍形海脊区域.
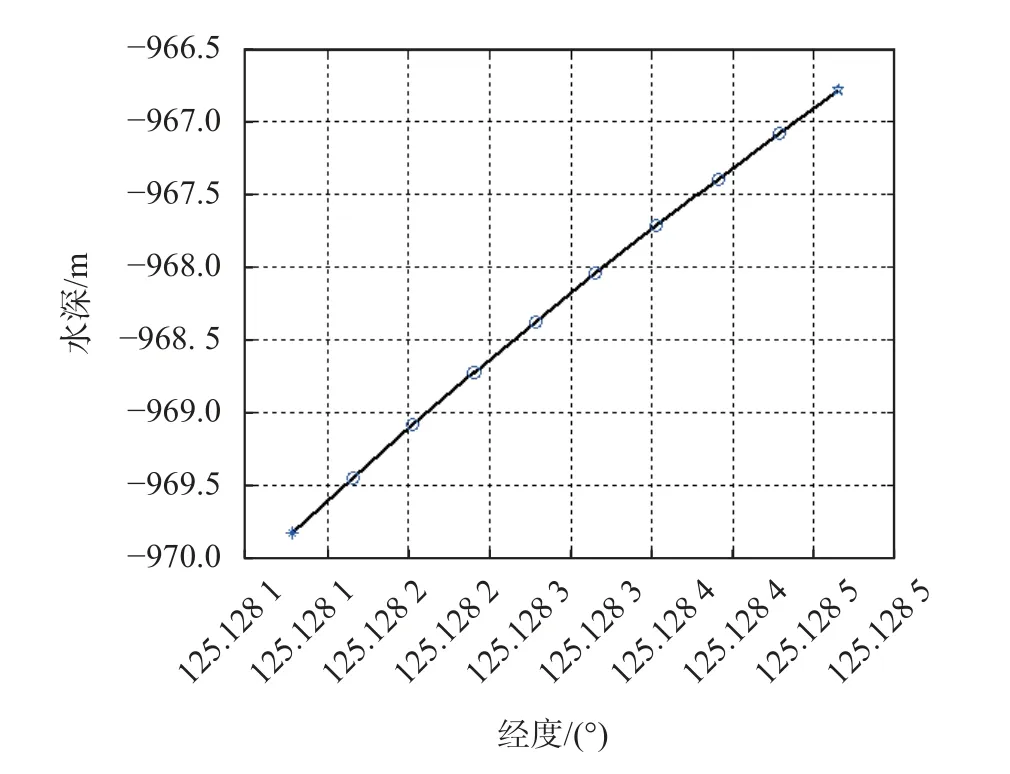
图4 航线中间波束经历处的水深
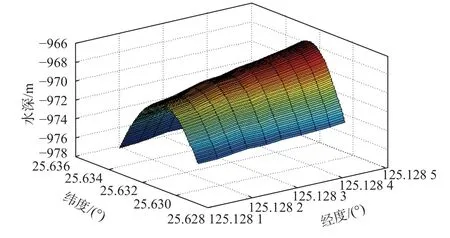
图5 扫描区真实水深图
2.1 测深改正
使用所设计的多波束模型进行扫描,两侧各8 条波束对称布设,由于回波是波束投射面内的最短距离,因此所获得的水深值较原始水深要浅,表现在马鞍两侧靠上部分向上凸起,比马鞍中间要高. 对获得水深重新进行样条插值如图6 所示.
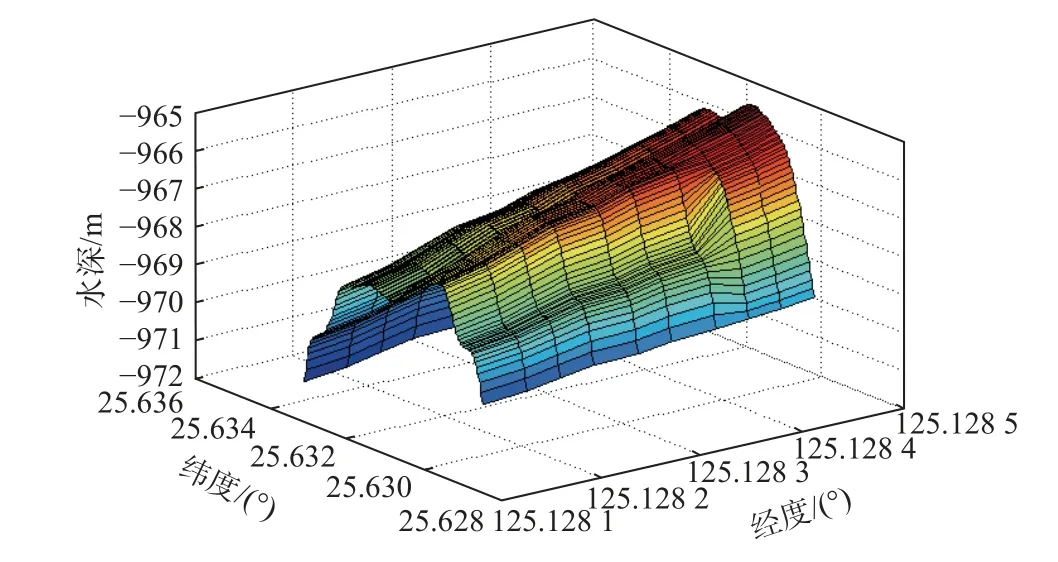
图6 多波束扫描改正前水深图
首先应用本文的水深改正算法对扫描图进行改正,然后进行样条插值,得到图7 所示的改正后水深,与图6 相比,两侧凸起部分被减小,与图5 真实水深相比,更符合马鞍形真实情况.
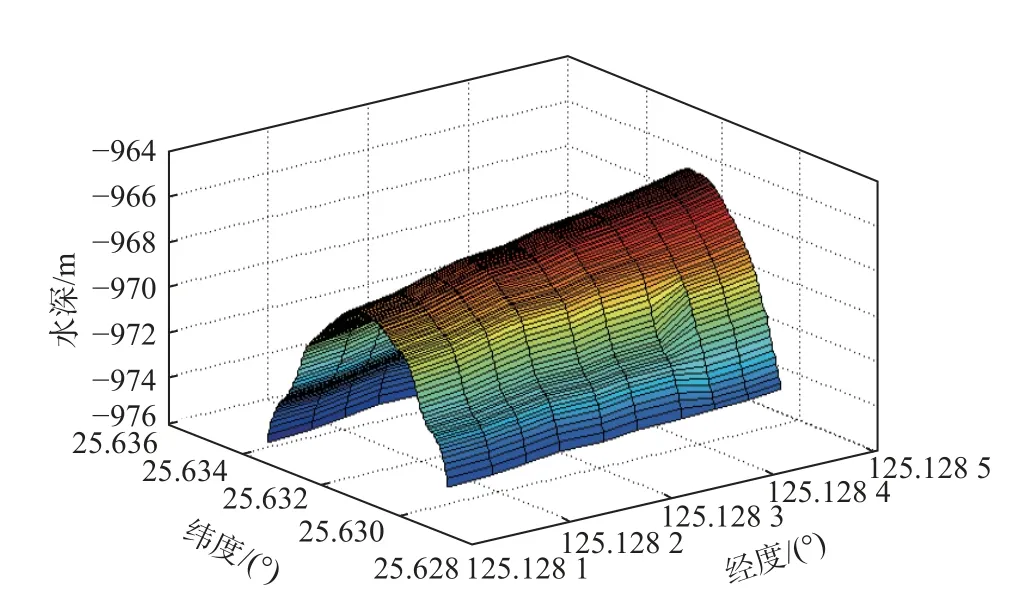
图7 多波束扫描改正后水深图
扫描过程中形成的脚印及测深改正后调整的脚印如图8 所示,由于改正后水深值产生了变化,脚印点需要根据改正后水深值进行重新调整.


图8 多波束扫描产生脚印改正前后对比
2.2 改正误差
应用本文定义的平均误差对水深扫描图中各点进行计算,改正前的误差曲面如图9 所示,可以发现,中间波束测深误差较小,随着波束靠近边缘,误差越来越大,沿着航线,呈现中间低、两侧逐渐变高扬起的特点,这与实际多波束系统是一致的. 通过改正,边缘波束的测量误差极大值减小,如图10 所示,同时减小了多波束系统测量的边缘效应.
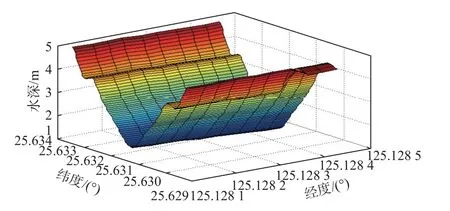
图9 多波束扫描改正前水深误差图
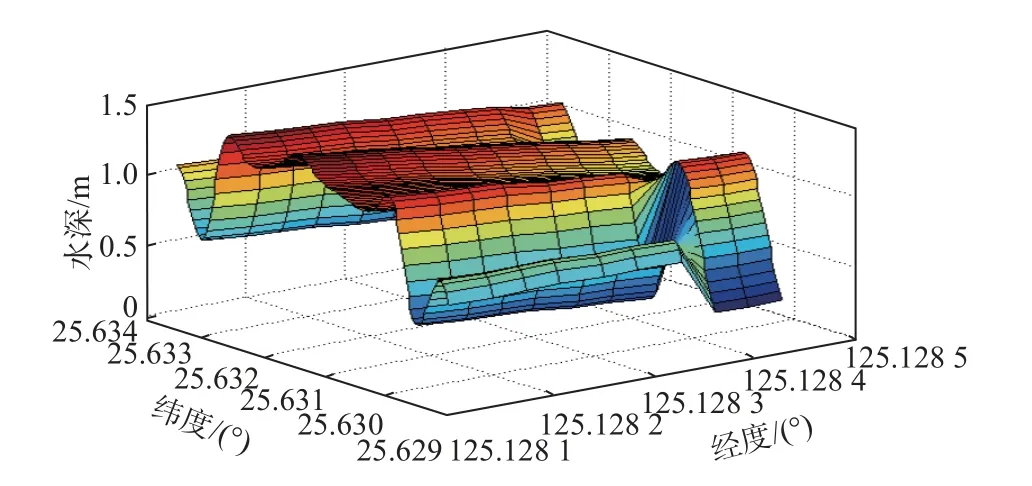
图10 多波束扫描改正后水深误差图
对改正前后形成的水深地图与真实水深地图之间的测深误差进行计算如表1 所示,包括两幅地图之间的平均误差和最大误差,表中发现,改正后误差获得明显减小,从而提高了地图精度.
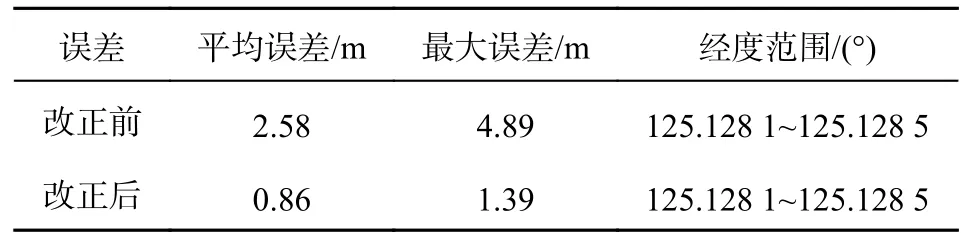
表1 改正前后误差对比
3 结束语
本文针对多波束水深测量中存在波束脚效应与地势效应引起测深误差问题,对水深测量值进行了改正. 首先依据多波束声纳系统水深扫描的原理,对其扫描过程建立模型,进行了测深扫描设计,继而对波束角和地势效应的相互作用建立了真实水深与测量记录水深的关系,这种关系与地形的倾角有关,然后通过测量点记录水深的8 点邻域平均坡度对地形的倾角进行估计,通过估计值对测量值进行了改正,以减小水深测量中的误差. 仿真中通过实际海底某区域的原始数据进行了验证,设置了航线,获得了扫描图形,并对航线两侧波束测量的水深进行了改正,并对改正误差进行了分析. 结果表明,这种改正一定程度上降低了记录水深与真实水深之间的误差,相应改善了海底地形测量的准确度.

