3D Target Localization Based on FrFT from Spaceborne Curve SAR

Zhitong Nie, Zhiyang Chen, Yuanhao Li, Cheng Hu

Abstract: Synthetic aperture radar (SAR) three-dimensional (3D) imaging technology can reconstruct the complete structure of observed targets and has been a hot topic. Compared with tomographic SAR, array interferometric SAR, and circular SAR, curve SAR can use less data to achieve 3D positioning of targets. Most existing algorithms for estimating Doppler frequency modulation(FM) rate are based on sub aperture partitioning, resulting in low computational efficiency. To address this, this article establishes a target height estimation model, which reflects the relationship between the height and the residual Doppler FM rate for spaceborne curve SAR. Then, a fast SAR 3D localization processing flow based on fractional Fourier transform (FrFT) is proposed.Experimental verification demonstrates that this method can estimate the Doppler FM of the target column by column, and the 3D position error for non-overlapping targets is controlled within 1 m. For overlapping points with an intensity ratio greater than 1.5, the root mean square error(RMSE) of the estimation results is around 5 m. If the separation between overlapping points is greater than 35 m, the RMSE decreases to approximately 2 m.

Keywords: three dimensional (3D) localization; fractional Fourier transform (FrFT); spaceborne synthetic aperture radar (SAR); curve trajectory

1 Introduction

Synthetic aperture radar (SAR) possesses the capability of all-weather, all-day, and high-resolution observation, making it a crucial tool in Earth observation [1, 2]. Conventional SAR twodimensional (2D) images can only provide a rough estimate of the target’s 2D location, lacking information about its height, and often encountering problems such as layover and topbottom inversion [3, 4]. This issue is particularly pronounced in densely built urban areas with complex structures. Cities hold significant strategic importance in modern warfare, which is selfevident [5]. Therefore, the precise estimation of target height and the reconstruction of its threedimensional (3D) structure are of utmost importance.

Over the years, SAR 3D imaging technology has seen several common approaches, including Tomographic SAR (TomoSAR), Array Interferometric SAR (InSAR) , and Circular SAR(CSAR). TomoSAR, often referred to as multibaseline SAR, involves the radar observation platform flying at different heights to repeat the process, creating a synthetic aperture in the height dimension, thus achieving high resolution in the range-elevation 2D plane [6]. Array InSAR, on the other hand, involves mounting multiple antennas on the observation platform,employing multi-input multi-output techniques to acquire multi-channel SAR images, enabling single-pass 3D imaging [7, 8 ]. Circular SAR involves the observation platform moving in a circular path around the target, capturing allaround target information [3]. Similarly, it can achieve high resolution in the range-azimuth and range-elevation 2D planes with just one flight,addressing the time-consuming issue of Tomo-SAR.

In terms of timeliness, these methods all require a large amount of data as the foundation,while the spaceborne curve SAR can achieve rapid 3D reconstruction of targets using a single channel. In military scenarios such as battlefield reconnaissance and damage assessment, where timeliness is crucial, this is of utmost importance.Since the satellite’s complete trajectory is circular, as long as the synthetic aperture time is long enough, it can capture the satellite’s partially curved path, forming a synthetic aperture in the elevation direction. Although the elevation synthetic aperture is relatively small, leading to lower resolution, it is possible to estimate the heights of the main points using parameter estimation methods.

The Naval Surface Warfare Center (NSWC)in the United States began researching the imaging mechanisms of curve SAR [9]. A study in [10]analyzed the distribution characteristics of scattering centers, enabling the reconstruction of the 3D structure of known target models but not for unknown targets. Another study in [11], using the TerraSAR-X staring spotlight mode, proposed a method to estimate the absolute height of a target based on the scattering behavior of point targets. This research confirmed the feasibility of estimating target height through spaceborne curve SAR. A spaceborne SAR 3D information extraction technique was proposed in [12],which utilizes the inversion of height information based on the Doppler frequency modulation(FM) rate error.

The above article employed the method of map drift (MD) to estimate the Doppler FM rate error. This method not only loses signal-tonoise ratio, but also leads to lower processing speed.

To address the above issues, this article proposes a 3D localization estimation method based on the fractional Fourier transform (FrFT),which offers the advantage of faster processing by estimating target parameters column-wise. In the rest of this paper, a new height estimation model is established in Section 2, a 3D target localization processing workflow is provided in Section 3,simulation experiments are conducted in Section 4,and conclusions are presented in Section 5.

2 Height Estimation Model

The essence of the 3D positioning method based on curve trajectory targets is to estimate the height from the residual Doppler FM rate after imaging. Therefore, we first need to derive a model of frequency modulation and target height.This is the main content of this section. The motion trajectory of the satellite is shown in Fig. 1. The satellite moves along a uniform circular path with a velocityv. Due to the very low orbit of the satellite, the Earth’s rotation effect can be ignored, and during satellite observation,the target can be considered stationary. When the synthetic aperture time is relatively short,the satellite’s angular displacementθis small,allowing us to calculate the satellite’s coordinates at a given moment based on its velocity at the synthetic aperture center moment.

Fig. 1 The satellite trajectory model

The angular displacementθcan be represented as

wheretais the slow time and belongs to(-Ts/2,Ts/2),Tsis synthetic aperture time,Rerepresents the Earth’s radius, andHsdenotes the satellite’s orbital height.

The coordinates of the satellite can be expressed as

By differentiating the satellite’s trajectory,we can obtain the velocity vector of the satellite as

In the same coordinate system, the target position model is shown in Fig.2, where pointArepresents a location on the ground,RAis the slant range from satelliteSto pointA, and pointBis the observed target point, and it is at a distance Δhfrom pointA.RBrepresents the slant range from the satellite to pointB, and it is equal toRA.

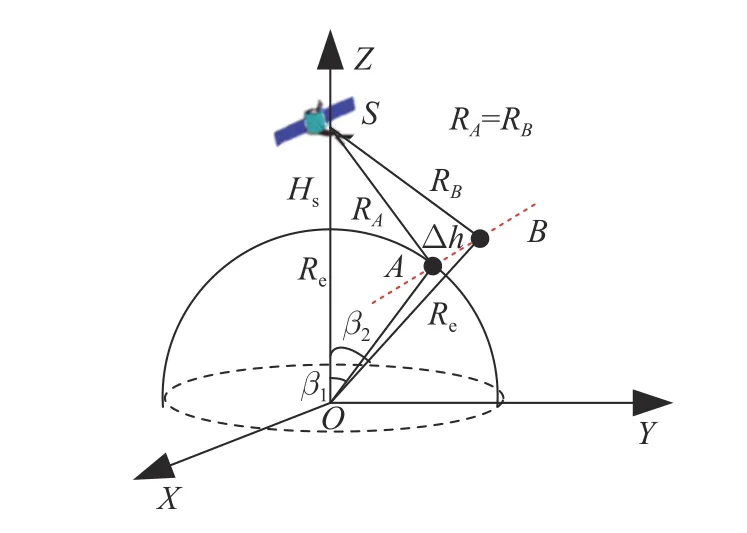
Fig.2 Observation geometry model

Based on geometric relationships, we can derive the coordinates of pointAand pointBas

whereβ1=∠SOAandβ2=∠SOB.

The range vector betweenSAandSBcan be obtained from the satellite’s position coordinates and the point target’s position coordinates,i.e.

The frequency of two points can be represented by

whereλrepresents wavelength.And the Doppler bandwidth for each of them can be shown as

As well as the difference in Doppler bandwidth between the two is shown as

Finally, the difference in Doppler FM rate between the two points ΔKacan be represented by

and derive the Δh

3 3D Localization Processing Workflow

From Eq.(13), it can be seen that there is a linear relationship between the target’s Doppler FM rate residual and its height.By obtaining the difference in Doppler FM rate between the target and the ground target, the target’s height can be estimated.Therefore, the processing workflow is divided into two parts: target imaging and parameter estimation.In the target imaging phase, the target’s position is determined, and a reference 2D spectrum is constructed based on the scene’s center.This spectrum is then conjugately multiplied with the 2D spectrum of the target point in the frequency domain to form the Doppler FM rate difference.In the parameter estimation phase, the FrFT is used to estimate the Doppler FM rate difference, and the target’s height is derived using Eq.(13).Additionally,the initial frequency is used to compute the target’s azimuthal position.The specific workflow is illustrated in Fig.3.

Fig.3 3D localization processing workflow

3.1 Target Imaging

To better illustrate the data processing workflow,this article establishes a scene coordinate system based on Fig.2.Firstly, the scene’s center is taken as the origin, the line connecting the Earth’s center to the scene center serves as thezaxis, the satellite’s velocity direction forms thexaxis, and the ground-range direction defines they-axis, as depicted in Fig.4.The echo spectrum of reference pointOis assumed as

whereσis the scattering coefficient;ωrandωastand for the range envelope and the azimuth envelope, respectively;τandηare the range time and the azimuth time, respectively;Kris the range FM rate;R(η) is the slant range history from the satellite to the scene center;cis speed of light.

Night represents the unconscious, the feminine principle, death, evil, germination, potentiality, darkness, the subconscious, the womb, and the precursor of creation (Olderr 1986).Return to place in story.

Fig.4 Scene coordinate system

Usually, curved trajectory spaceborne SAR uses a longer synthetic aperture time to locate the target (close to 10 s) and cannot be represented by a second-order polynomial.Therefore,a fourth-order polynomial is used here.From satellite tool kit (STK) verification, it shows that the error is only on the order of 10-4m.The polynomial expression forR(η) is

whereR0is the constant term andk1,k2,k3andk4are the coefficients.Under curve-based trajectories, traditional range-Doppler (RD) imaging methods are no longer applicable.Therefore, this paper adopts frequency domain imaging techniques.Ref.[1] proposed a reference 2D spectrum for the scene center under a curved but only expandedfato the fourth order.However,the system in this paper is for spaceborne SAR long-time observation.The satellite platform follows a relatively long curved trajectory.The fourth-order spectrum offacannot precisely depict the spectral model, due to the presence of residual phase, resulting in ground targets appearing defocused during imaging.Therefore,in this article, the standard 2D spectrum is expanded into the sixth-order terms offa.The spectral expression is shown as

wherefrandfastand for the range frequency and the azimuth frequency, respectively;fcstands for signal frequency.

From Eqs.(13) and (16), it can be observed that the original Doppler FM has a nonlinear relationship with target altitude.However, after the echo undergoes matched filtering with the ground target, a linear relationship between residual Doppler FM and target altitude can be seen.

By multiplying the Echo spectrum with the complex conjugate of this reference 2D spectrum,followed by an inverse Fourier transform, the imaging result can be obtained.Due to inconsistency between the positions of the target point and the reference point, this result includes the Doppler FM rate residual of the target.

3.2 Parameter Estimation

In order to rapidly estimate the frequency differences of all target points, this paper employs the FrFT to estimate the target points’ frequency and initial frequency.The FrFT is a common tool for processing non-stationary signals [13] and is particularly accurate for linear frequency modulated (LFM) signals, making it capable of simultaneously estimating the frequencies of multiple target points as well as the initial frequency.Over the years, many scholars have proposed fast algorithms, with one of the more notable being the improved FrFT algorithm introduced by Haldun M.Ozaktas, which utilizes fast Fourier transformation (FFT) to reduce algorithm complexity [14].Its definition is shown as

The FrFT is applied column by column to estimate target parameters.Therefore, it is possible to locate the target positions based on the SAR image after imaging.Then, the signal along the azimuth direction is extracted for FFT,allowing for the simultaneous estimation of multiple targets.At this point, the signal is in the frequency domain and contains Doppler FM rate residuals.Finally, the FrFT is applied to this frequency domain signal.

When using FrFT, since the time domaintand frequency domainfhave different units, it is necessary to transform both the time domain and the frequency domain into dimensionless domains.Introducing a scaling factorQ, we define new scaled coordinates as

In estimating the initial frequency and Doppler FM rate of the signal, the properties of linear LFM in different FrFT domains can be utilized.The process is as follows:

1) First, the signal, which has undergone scaling transformation, is subjected to FrFT transformation with different ordersp, resulting in a 2D energy distribution map in thep-uplane.

2) Next, the peak positions of the energy are searched for in this map.

From Eq.(22) , the difference in Doppler FM rate between target pointBand the scene center pointOin the frequency domain is obtained.As the time-domain frequencyKOat pointOcan be obtained through fitting, the time-domain FM rate at pointBcan thus be determined as

Then the difference in FM rate between the two points in the time domain can be obtained as

Due to the model established in Section 2,which uses pointAas the reference point, we now need to calculate the position of pointAin the ground-range directionAybased on the geometric relationship in Fig.4.

whereSyis the satellite’sycoordinate at the moment of the synthetic aperture center, andShis the satellite’szcoordinate at the moment of the synthetic aperture center.

By fitting the slant range, we can determine the FM rateKAof the reference pointA.By using Eqs.(24) and (26) , the difference in Doppler FM rate between pointsAandBcan be obtained as

By substituting Eq.(27) into Eq.(13), the height difference Δhcan be obtained, that isBz.Finally, compute the ground-range coordinate of targetB, which is

Now, we have obtained the 3D position of targetB.

4 Simulation Experiment

To verify the effectiveness of the proposed method, this paper conducted single-point and multi-point simulation experiments.The satellite trajectory and velocity were obtained using STK,and the orbital elements are shown in Tab.1.Other simulation parameters are presented in Tab.2, where the range resolution is 1.5 m, and the azimuth resolution is 0.2 m.We chose a higher sampling rate ( 2.5 times bandwidth instead of 1.2 times) for better observation of the imaging results of the target points. From Ref. [15],we can learn that for a practical spaceborne SAR working in spotlight mode, PRF variation is conventionally employed to resolve the problem of fixed blind ranges as well as the conflict of high resolution and wide swath. This paper aims to validate the principles and feasibility of the algorithm, thus omitting the step of converting original PRF to equivalent PRF and directly treating the equivalent PRF as the input PRF.

Tab.1 Orbital elements

Tab.2 Simulation parameter

4.1 Single Point Simulation

In the scene coordinate system, the coordinates of the target pointT1 are set to [15, 15, 50].First, the echo is constructed, and then it is multiplied by the complex conjugate of the reference spectrum, yielding the imaging result shown in Fig. 5. From Fig. 5, it can be observed that due to the presence of height in the target, there is defocusing in the azimuth direction. To show the defocusing condition, Fig. 5 (b) shows the imaging result of point [15, 15, 0]. And an azimuth profile plot was generated showing in Fig. 5 (c).

The result of applying FrFT to the column containing the target is shown in Fig. 6. From Fig. 6, it can be observed that a single target in theu-pplane will exhibit only one peak. The transformation orderpis 0.994 6. Based on the position of this peak, the target parameters can be estimated. The final estimation results are shown in Tab. 3.

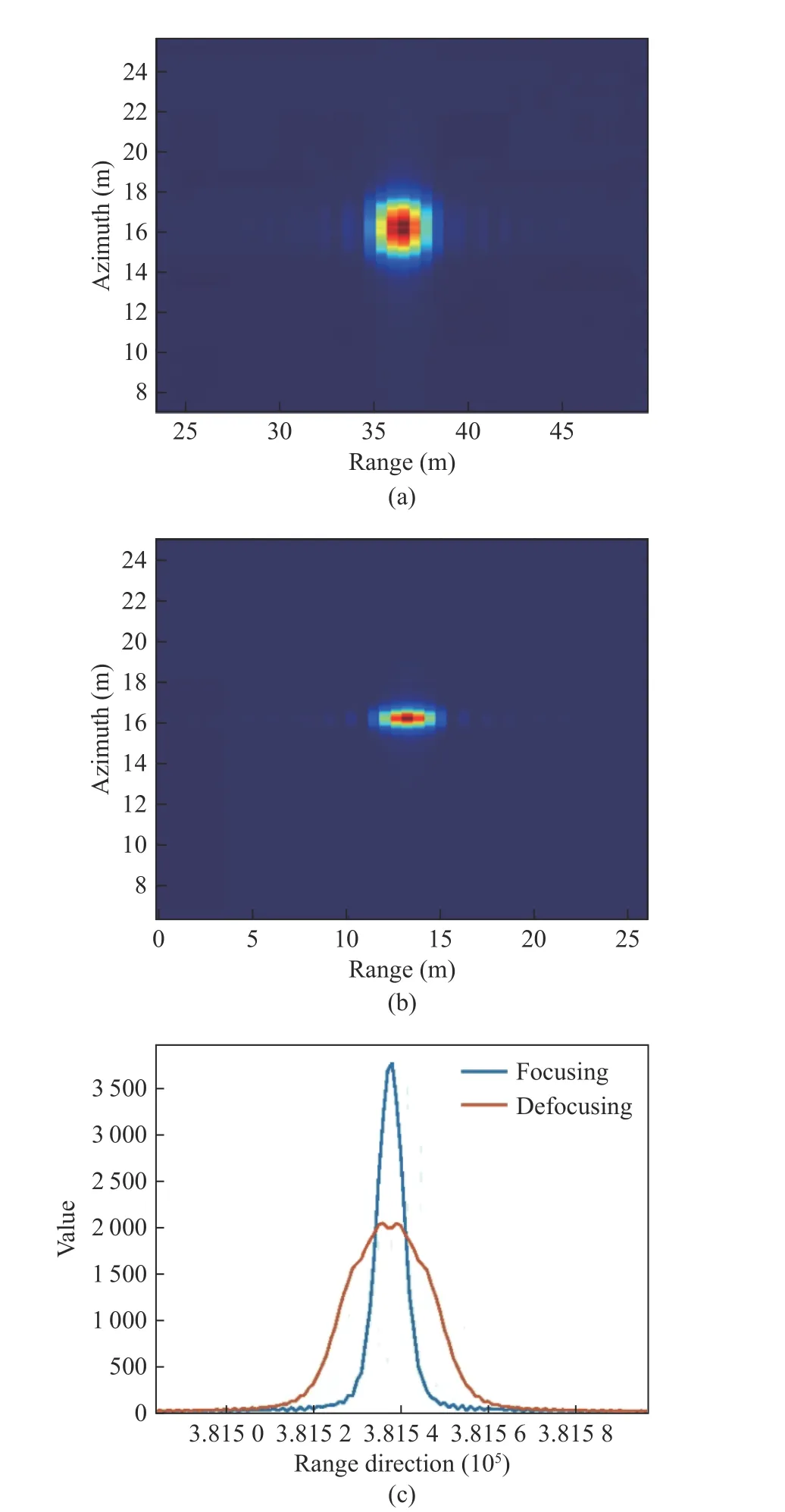
Fig. 5 Single point imaging: (a) defocusing result; (b) focusing result; (c) azimuth profile plot

Fig. 6 Single point FrFT result

Tab.3 Single point estimation results

From Tab. 3, we can see that this method provides accurate estimation for a single-point target. The errors in all three dimensions for the single-point target are within 1 m, indicating a precise localization of the target position.

4.2 Multi-Point Simulation

In modern cities, many buildings have a significant amount of glass on their exteriors, which results in dihedral angles, leading to isolated strong points in the radar echoes from these structures. Therefore, by estimating the 3D positions of these isolated strong points, it’s possible to reconstruct the 3D structure of the buildings.This paper simulated scenarios with multiple isolated strong points, demonstrating the method’s ability to estimate the positions of multiple points. The input target positions and the estimated target positions are shown in Tab. 4.

The multi-point imaging result is shown in Fig. 7. It can be observed thatT2 andT4 are in the same azimuth direction, whileT2 andT3 are in the same range direction. Therefore, when esti-mating the positions of these two points, only the respective columns need to be considered.

Tab.4 Multi-point simulation results

The FrFT results are shown in Fig. 8. It can be seen from Fig. 8 that if there are multiple points in a certain range direction, the FrFT results will also exhibit multiple peaks. Similarly,based on the positions of these peaks, the parameters of the targets can be estimated.

From Tab. 4, we can observe that in the case of targets with certain intervals, this method provides accurate estimation for multi-point targets. The errors in all three dimensions for the multi-point targets are within 1 m, demonstrating the capability of this method to accurately locate multiple target positions.

4.3 Strong Scattering Points Simulation

To validate the estimation performance of this method for strong targets, two targets were set at the same slant range and azimuth positions,with Target 1 at varying heights of 15 m, 25 m,35 m, 45 m, and 55 m, and Target 2 at a height of 5 m. A total of 100 repeated experiments were simulated with different intensity ratios of 1:1,1.1:1, 1.3:1, 1.5:1, 1.8:1, 2:1, 2.5:1, and 3:1. The average error and root mean square error(RMSE) of the estimation results from this method were calculated.

Fig. 7 Multi-point imaging: (a) defocusing result;(b) focusing result

Fig. 8 Multi-point FrFT results: (a) FrFT results for the column containing T2 and T3; (b) FrFT results for the column containing T4

The results in Fig. 9 indicate that when the intensity ratio between the two targets is greater than 1.5:1, this method achieves an estimation accuracy for strong target heights within 1 m.Furthermore, as the intensity ratio increases, the accuracy gradually improves, and the RMSE decreases progressively.

Fig. 9 Strong scattering points simulation results: (a) average error of different amplitude ratios; (b) RMSE of different amplitude ratios

5 Conclusion

This paper proposes a novel satellite-based altitude estimation model, derives the relationship between Doppler FM rate error and target height, and introduces a 3D target localization processing workflow. FrFT is employed to estimate the Doppler FM rate and initial frequency information of the target echo. In terms of the ability to resolve overlapping points, this method is not as strong as tomographic SAR. However,in terms of timeliness, this approach can complete 3D reconstruction with just one flight.

To validate the 3D positioning capability of this method, we conducted simulation experiments for single-point and multi-point targets.The results indicate that the positioning error in all three dimensions is within 1 m. Furthermore,to assess the estimation performance of this method for overlapping points, we simulated the estimation of overlapping points at different heights with varying intensity ratios. The results show that when the intensity ratio of overlapping points is greater than 1.5 and the separation is greater than 35 m, the RMSE of the estimation results is around 2 m.