Post-Processing of InSAR Deformation Time Series Using Clustering-Based Pattern Identification
Wenxin Zhu, Fengming Hu, Feng Xu
Abstract: Multi-temporal synthetic aperture radar interferometry (MT-InSAR) is a standard technique for mapping clustering and wide-scale deformation.A linear model is often used in phase unwrapping to overcome the underdetermination.It’s difficult to identify different types of nonlinear deformation.However, the interpretation of nonlinear deformation is very important in monitoring potential risk.This paper introduces a comprehensive approach for identifying and interpreting different types of deformation within InSAR datasets, integrating initial clustering and classification simplification.Initial classification is performed using the K-means clustering method to cluster the collected InSAR deformation time-series data.Then we use F test and Anderson-Darling test (AD test) to simplify the clusters after initial classification.This technique distinctly discerns the changing trends of deformation signals, thereby providing robust support for interpreting potential deformation scenarios within observed InSAR regions.
Keywords: multi-temporal synthetic aperture radar interferometry (MT-InSAR); machine learning;hypothesis test; nonlinear deformation
1 Introduction
Multi-temporal synthetic aperture radar interferometry (MT-InSAR) technique has garnered significant attention in recent years due to its highresolution imaging capabilities, all-weather observation capabilities, and sensitivity to surface features [1-3].By analyzing the interferometric images acquired by radar satellite sensors, InSAR has demonstrated the ability to detect millimeter-level surface deformations [4, 5], offering substantial support for studies encompassing geological hazards [6], crustal movements [7, 8], land subsidence [9], and more.
Nevertheless, as satellite revisit periods continue to shorten, the volume of InSAR datasets has been experiencing rapid growth [10, 11].Presently, an InSAR dataset can encompass millions of scatterers, presenting challenges in efficiently processing these extensive datasets in practical applications [12].
In fact, the acquisition of large-scale InSAR data introduces complexities to the analysis of ground scatterer deformations [13, 14].Each scatterer’s deformation information is constructed from multiple observations at various times.The vast amount of interferometric images necessitates effective processing and resolution to extract accurate displacement information.Additionally, factors like atmospheric noise [15-17]often influence surface deformation resolution,further complicating deformation analysis.
In the past, researchers often employed fixed linear models for InSAR deformation processing,representing surface deformations as simple linear velocity changes [18, 19].However, real-world InSAR signal processing frequently reveals nonlinear deformation features, such as seismic activities or surface collapses [20, 21].Previous postprocessing methods for InSAR signals often struggled to fully capture complex deformation patterns associated with non-linear deformations,limiting their effectiveness [22].
Many researchers have explored the application of statistical methods to InSAR data processing.Statistical testing techniques such as analysis of variance (ANOVA) are used to classify ground deformations into seven major trends:stable, linear, quadratic, bilinear, phase unwrapping error (PUE), constant, and variable speed discontinuities [23].Systematic evaluation of competitive motion models was carried out using a probability approach based on multiple hypothesis testing (MHT), enabling the identification of optimal models and the assignment of probabilities to results, effectively monitoring motion behavior of numerous points and objects on earth[24].
Recently, machine learning clustering methods have emerged as efficient and accurate tools for handling massive datasets [25, 26 ].These methods encompass both supervised and unsupervised learning.Supervised learning utilizes labeled data for model training to predict and classify new data.Random Forest and Extreme Gradient Boosting models are applied to classify Differential Synthetic Aperture Radar Interferometry (DInSAR) time series, identifying ground deformation trends [27].Bidirectional Long Short-Term Memory (BiLSTM) classification models are employed to categorize ground subsidence deformations on Coherent Scatterers(CCS), particularly identifying anomalies like abrupt changes in mutation and mutation rates[28].
Conversely, unsupervised learning does not rely on pre-labeled data but rather learns from inherent structures and patterns within unlabeled data.An unsupervised automated approach based on principal pomponent pnalysis (PCA)and K-means clustering for detecting natural or anthropogenic ground deformation patterns within InSAR time series was introduced [29].A method for monitoring surface deformation was proposed using t-distributed stochastic neighborhood embedding (t-SNE) dimension reduction and density-based spatial clustering of applications with noise (DBSCAN) clustering.This approach significantly improved data interpretability by modeling deformation behavior for each scatterer, enhancing the quality of timeseries deformation assessment [30].By learning patterns and relationships from data in a supervised or unsupervised manner, these methods accurately describe non-linear deformations, providing more detailed interpretation results.
In this study, we proposed a comprehensive technique that combines machine learning and statistical learning methods for processing surface deformation information within InSAR data.Specifically, we employ theK-means clustering method to identify distinct deformation patterns and introduce parametric and non-parametric hypothesis testing methods for iterative optimization, achieving more accurate deformation interpretation and post-processing of InSAR time series signals.
This paper is structured as follows: Section 1 reviews various MT-InSAR time series processing techniques.Section 2 details the methodology and principles employed in this study, along with the corresponding flowchart.Section 3 showcases the application of our proposed methods in the Dishui Lake area of Shanghai, encompassing data processing and result analysis.Finally, Section 4 summarizes research outcomes and discusses avenues for future improvements.
2 Methodology
This section will introduce the methods used in this study in detail.First, we will introduce the deformation processing method for scatterers,which is the basis of this study.We will then give a brief introduction to the principles ofKmeans clustering, a method used for the initial classification of InSAR data.Then, we introduce the principles of AD test and F test, which are used to evaluate the distribution and variance of the data and simplify clusters.Finally, we will describe the entire workflow in Section 2.5..
2.1 InSAR Data Processing
The InSAR technique is based on the interferometric effect of radar beams, measuring subtle surface deformations and changes by comparing the phase differences between two or more SAR images [31].The interferogram is generated by conjugate multiplication of two co-registered SAR images, and the interferometric phase encompasses the changes in distance between the satellite and ground targets during two observation periods.These changes in distance are caused by various factors, and the interferometric phase for each pixel can be expressed as [32]:
The main factors that cause the distance change are flatten phaseϕflat, topographic phaseϕtopoand deformation phaseϕdefo.The last three items are considered as noise items in processing,which in turn are satellite orbit error phaseϕorbit,atmospheric delay phaseϕatmoand noise phaseϕnoise,nrepresenting phase ambiguity and phase wrapping operation.
After estimating the linear deformation and elevation error for the interferometric phase model for each arc segment formed by every two initial Persistent Scatterer (PS) points, the corresponding residual phase can be obtained.As the dominant components of the interferometric phase have been removed, the residual phase variation becomes smoother, devoid of ambiguity,and suitable for direct spatial phase unwrapping to obtain the residual phase for each PS.The unwrapped residual phase contains atmospheric phase, non-linear deformation phase, and noise phase.By removing the atmospheric phase from the unwrapped residual phase, the non-linear deformation phase and noise phase can be extracted.Coupled with the calculated linear deformation phase, this allows for the generation of deformation time series.
2.2 Initial Clustering
Clustering is an efficient way to classify the dataset.Here we useK-means clustering as an initial classification method to demonstrate scatterers’ deformation [[33].K-means clustering is an unsupervised learning algorithm used to partition data intoKdistinct clusters.Its principle involves iteratively assigning data points to the nearest cluster centroid through optimization.Given a dataset and a specified number of clustersK, the objective ofK-means clustering is to divide data points intoKclusters in a way that maximizes the similarity within each cluster while maximizing differences between different clusters.The algorithm’s core idea revolves around iterative optimization, continually adjusting cluster centers to eventually determine a set of cluster centers that minimize the overall distance between data points and cluster centers.
Assuming a datasetX={x1,x2,...,xn}, a specified number of clustersK, and a set of cluster centersC={c1,c2,...,cn}are given, the distance between data points and cluster centers can be represented using the Euclidean distance
wheredis the dimension of the data point.Assign data points to the nearest cluster center
Then update the cluster center to the mean of all data points in the cluster
whereSjis the collection of data belonging to the clusterj.By iterating the above steps, theK-means clustering algorithm continuously optimizes the cluster center, making the distribution of data points more compact and the intra-class similarity higher.In this study, we will useKmeans to preliminarily classify the deformation time series of InSAR scatterers and subdivide the deformation sequence into many small classes.s.
2.3 Clustering Simplification
Clustering manually sets the number of clusters.However, there are always similar clusters in the initial classification.Instead of manually setting the number of categories, we want to use significance level indicators to automatically simplify the initial clustering results.In this part, we will use parametric hypothesis testing and non-parametric hypothesis testing to get initial clusters simplified.
2.3.1 Non-Parametric Hypothesis Testing
In this part, we use AD test as a classical nonparametric hypothesis testing method for clustering simplification.The AD test is commonly employed to assess whether data originates from a specific distribution [34].Its fundamental concept involves comparing the disparities between a data sample and a theoretical distribution.It calculates a statistic that measures the goodness of fit between observed data and the theoretical distribution.A larger value of the statistic indicates a poorer fit between the data and the theoretical distribution.In other words, if the value of the statistic significantly exceeds a critical threshold, it allows us to reject the hypothesis that the data comes from the theoretical distribution.
Due to the substantial differences in linear trends among various time series, the fit between data and the theoretical distribution would be notably poor if it is not eliminated.This could result in an inadequate fit betweenK-means clustering outcomes and the distribution..
We use a linear regression model for each time series, fitting the data points onto a straight line of the formy=mx+b, wheremis the slope andbis the slope distance.We calculate the predicted value of each sequence on the fitting lineyˆ and then subtract the predicted value from the original observation to get the detrended data.Remove the linear trend as follows:
Therefore, for each data point (ti,yi), its predicted valueyˆiis expressed as
After removing the linear trend term, the deformation data is transformed into
Then, we apply AD test to the data to determine whether different categories afterKmeans clustering obey the same distribution, as follows::
wherenis the sample size andF(ydetrend,i) is the value of the cumulative distribution function of the theoretical distribution atydetrend,i.
The greater the AD statistic is, the greater the deviation of the observed data from the theoretical distribution will be.The calculated statistics are then compared with the critical value for hypothesis testing.
2.3.2 Parametric Hypothesis Testing
This paper also employs a parametric hypothesis testing method called the F test to determine whether different categories afterK-means clustering follow the same distribution [35].We will also remove the linear trend from the sequences first (see Section 2.3.1).When conducting the F test hypothesis test, we set the null hypothesis H0as equal variance between the two samples and the alternative hypothesis Hias unequal variance between the samples.The fundamental idea of the F-test is to compare the variances of two (or more) groups of samples and determine if these sample variances are significantly different by calculating the F-ratio.If the computed F-ratio is greater than a certain critical value,the null hypothesis can be rejected, indicating unequal variances among the samples.Otherwise,if the computed F-ratio is not greater than the critical value, the null hypothesis cannot be rejected, implying equal variances among the samples.This critical value is based on the chosen significance levelα.
2.4 Flowchart of Deformation Pattern Identification
Flowchart of this study is illustrated in Fig.1,encompassing the following steps: initially, we employK-means clustering to group InSAR data,where a relatively large value is set for the number of clusters (K) to achieve finer grouping.Subsequently, centroids and quartiles (i.e., the 25th and 75th percentiles) are extracted from each group.Both F test and AD test are applied to remove linear trends of InSAR deformation time series and assess data distribution and variance.The purpose of this step is to compare the effectiveness of clustering simplification using parameterized and non-parameterized testing methods, respectively.Next, we merge columns with strong correlations and consolidate sequences exhibiting similar deformation trends,utilizing significance levels as merging criteria.Lastly, we iteratively perform the aforementioned steps to generate new centroids and quartiles and reapply the statistical testing process until convergence is reached, thereby obtaining the final deformation analysis results.

Fig.1 Flowchart of deformation pattern identification
Through the aforementioned approach, our aim is to analyze deformation patterns within InSAR data and identify crucial features therein.This endeavor will contribute to a more profound comprehension of surface deformation processes and establish a foundation for subsequent interpretation and applications.
3 Results
3.1 Study Area
To practically validate the feasibility of the aforementioned approach, we applied this method to the Dishui Lake InSAR dataset.Dishui Lake is situated in the Pudong New Area of Shanghai,China, characterized by its picturesque lake region.Its central coordinates are approximately 30°54' N and 121°56' E.Dishui Lake takes on a circular shape with a diameter of 2.66 km and a total area of 5.56 km2.The lake accommodates three islands with a combined area of 0.48 km2,while a 60 m wide park belt extending around the lake spans an area of 500 000 m2.The geological structure and surface deformation of the surrounding Dishui Lake area render it an ideal location for the application of InSAR technology in deformation monitoring.For this study,InSAR deformation time series were collected from Dishui Lake and its adjacent regions to facilitate the research.
Fig.2 is the image of Dishui Lake and its surrounding area displayed on Google Earth,which is also the area of our study.

Fig.2 Optical image of Dishui Lake area (Copyright GoogleEarth)
3.2 InSAR Data
We gathered a comprehensive collection of InSAR continuous scatterer deformation time series data covering Dishi Lake and its surrounding regions using satellite sensors.This extensive dataset comprises 338 646 scatterers and spans from July 2016 to July 2018.The data encompasses vital information such as surface deformation rates and directions, thereby forming the groundwork for subsequent analyses.We have plotted the linear deformation velocities as shown in Fig.3.It can be observed that there is a certain spatial pattern in the deformation trend of the scatterers, but the variation characteristics are not very distinct.Therefore, more analysis and research are required.

Fig.3 Linear deformation velocity on scatterers in Dishui Lake, Shanghai
3.3 Initial Clustering
We initially applied theK- means clustering method to cluster the collected InSAR deformation time series data.By selecting an appropriate number of clusters (K), we partitioned the time series data into different clusters.This aided us in analyzing deformation patterns and trends in various regions.
In initial clustering, we hope to categorize the scatterers into abundant classes so that the deformation trends of different categories of scatterers can be observed from the beginning.However, after trying to set differentKvalues, we soon found that when the initial valueKis set too large, there are a significant number of columns with similar deformation trends.Therefore, based on controlling computational complexity and considering the ease of subsequent category simplification, we chooseK= 15 as the initial value for the subsequent calculations.
Fig.4 shows the clustering results whenK=15 classes are set.Fig.5 displays the geographical distribution of different class scatterer data,used for analyzing the differences and similarities between clusters.Fig.6 depicts the deformation trends of the centroids and quartile lines of different classes’ deformation sequences.As observed, some categories exhibit similar deformation trends, indicating that further iterations are needed to refine the current clustering results.

Fig.4 K-means cluster scatterers quantity distribution
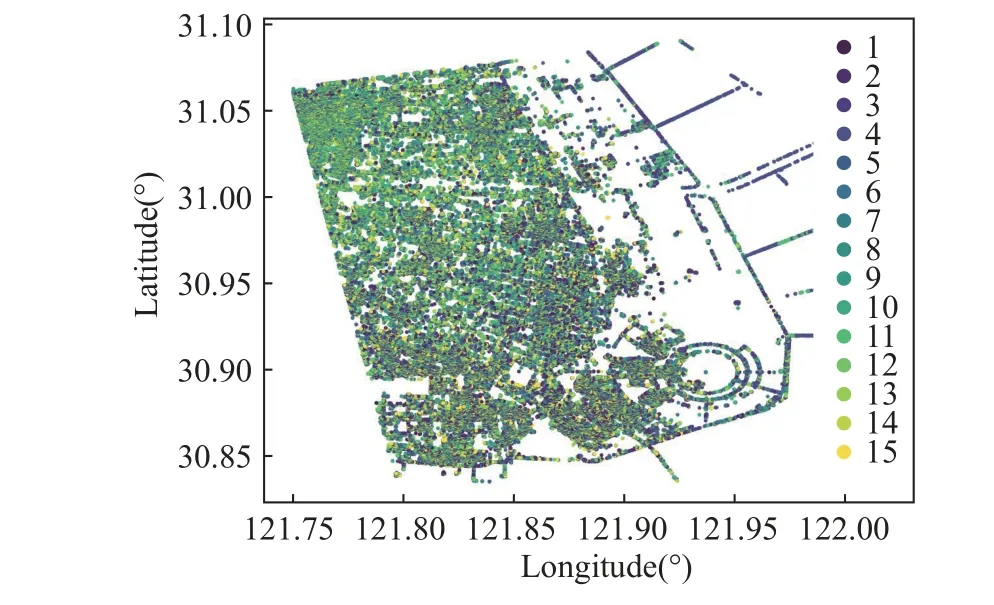
Fig.5 K-means cluster scatterers spatial distribution
3.4 Clustering Simplification
3.4.1 Non-Parametric Hypothesis Testing
On the basis ofK-means clustering, we apply AD test as a kind of non-parametric hypothesis testing method to evaluate whether deformation data of different classes obey the same distribution.We removed the linear trend component for the centroid and quartile lines of 15 types of deformation sequences and conducted AD test.The processing results are shown in Fig.7, and it can be seen that the deformation sequences only retain nonlinear features, which is very effective for our further application of AD test.We can easily classify the deformation sequences with the same nonlinear features into one class.From Fig.7, it can be observed that the original 15 classes of deformation sequences have been merged into 5 classes.Due to the presence of linear trends and the large vertical dimension, it is difficult to clearly represent the nonlinear trend of the red curve in Fig.7.We will discuss the characteristics of deformation trends after AD test in detail in Section 3.5.
The distribution of scatterers is depicted in Fig.8, showing the distinct positional characteristics of these scatterers.This outcome is determined by the characteristics of AD test.The AD test is highly sensitive to variations in sample data trends, allowing it to classify deformation sequences of scatterers, after removing linear trends, into different categories based on different distributions.Therefore, when scatterers exhibit similar nonlinear features, AD test can automatically group them into the same category.
3.4.2 Parametric Hypothesis Testing

Fig.6 Deformation trend of various centroid and quartile lines after K-means clustering (The red lines represent the centroid curves of each class, and the gray lines represent the 75% and 25% percentile lines)

Fig.7 Classification situation after AD test when significance level α = 0.2 (The black line represents the original centroid curve, and the red line represents the centroid curve after the linear trend is removed)

Fig.8 Spatial distribution of scatterers after AD test
In addition to the AD test, we also try to use variance as an indicator to distinguish between different deformation trends.By calculating the F ratio and comparing it with the critical value,we can decide whether to reject the null hypothesis of equal variance between clusters.We will show the results of the F test and analyze the variance difference between different clusters.When adjusting the significance level toα= 0.2 and after iterations, the scatterer sequences were eventually divided into 6 classes.

Fig.9 Spatial distribution of scatterers after F test
Fig.9 displays the deformation distribution of scatterers around Dianshui Lake after the F test.It can be observed that the clustering results exhibit similar trends to those obtained from the AD test.Further details and differences will be discussed in detail in Section 3.5.
3.5 Discussion
By comparing Fig.8 and Fig.9, it can be seen that after clustering simplification using F test or AD test, sequences are clustered into different categories characterized by regional distribution.Among them, in the area of clusterC= 2, it can be clearly seen that most deformation sequences are effectively identified as the same type of sequences, which also cross-confirms the effectiveness of parametric and non-parametric category simplification methods.In addition, combined with Fig.10, we can also see that the classification results of the two methods are also different.According to the analysis, we believe that this is because the F test is used to compare whether the variances between different groups are significantly different, while the AD test is used to test whether the data comes from a specific theoretical distribution, so the nonlinear characteristics are detected during classification not exactly the same.

Fig.10 Deformation clustering results for all scatterers: (a)-(f) applied by F test; (g)-(k) applied by AD test

Fig.11 Deformation trends of centroids and quartiles of each scatterer cluster: (a)-(f) applied by F test; (g)-(k) applied by AD test(The red lines represent the centroid curves of each class, and the gray lines represent the 75% and 25% percentile lines)
Fig.10 illustrates the clustering of all scatterers after simplification through both parametric and non-parametric hypothesis testing methods.The first row represents the results of F test,while the bottom row represents the results of AD test.In Fig.11, the deformation trends of the centroids and quartiles of each scatterer cluster are displayed.Despite there being some variations in the final number of categories resulting from simplification, it is still easy to find that several scatterer clusters exhibit identical clustering effects.Additionally, the centroids and quartile curves generally demonstrate similar deformation trends.This serves as mutual verification of the effectiveness of our algorithm, as it can automatically select scatterer sequences with similar nonlinear deformation trends.
For categories where the classification results differ, we attribute it to the distinct principles of AD test and F test algorithms.AD test primarily focuses on whether sample data follows a specific distribution, such as whether they all belong to a normal distribution.Its objective is to compare the similarity of fit between observed data.In contrast, F test, as a variance-based detection method, mainly emphasizes the comparison of variances among two or more groups of data.Its goal is to group deformation sequences with similar variances into one category.
In Section 3, the algorithm is applied to the temporal InSAR deformation sequence of Dishui Lake and its surrounding areas.The results show that the proposed method is quite applicable, and the features in the deformation sequence can be extracted and classified.In this paper, the significance level is used instead of a prior class number or critical value as the standard for the classification of deformation categories, which improves the generalization of InSAR sequence post-processing method.
4 Conclusions
This paper introduces a pattern identification approach that combines machine learning with hypothesis testing models for identifying different types of nonlinear deformation.TheK-means clustering is used to get the initial classification and the hypothesis test is used to evaluate the similarity of different clusters.To improve the robustness, both centroids and quartiles of the initial clusters are used in the classification simplification.Additionally, both non-parametric and parametric hypotheses are used to simplify the initial classification, showing that the parametric way is more suitable in the identification of nonlinear deformation.The demonstration in this work shows a fast and effective way to identify different types of nonlinear deformation,which contributes to the automatic interpretation of surface deformation on a large scale..
Acknowledgment
The authors would like to thank maps from Google Earth 2023, Shanghai, China, 30°N, 121°E(September 2023) for offering optical images.
 Journal of Beijing Institute of Technology2023年6期
Journal of Beijing Institute of Technology2023年6期
- Journal of Beijing Institute of Technology的其它文章
- Nonlinear Trajectory SAR Imaging Algorithms:Overview and Experimental Comparison
- 3D Target Localization Based on FrFT from Spaceborne Curve SAR
- Modeling and Analysis of the Impacts of Temporal-Spatial Variant Troposphere on Ground-Based SAR Imaging of Asteroids
- Cosserat Dynamic Modeling and Simulation of Mobile Cable on Satellite
- Analysis and Experimental Study on the Friction Force at the Binding Point of Flexible Cable on Satellite
- SAR Tomography with Improved Non-Local Means Filtering Based on Adaptive Window
