柴油车尾气智能检测诊断系统设计

黄万友,邹于建,谭世威,郭雅晶,褚瑞霞,刘冬影

山东交通学院汽车工程学院,山东济南 250357

0 引言

随着我国机动车保有量逐年增加,排放不达标的柴油车越来越多,污染物排放十分严重,对其进行有效治理迫在眉睫。全国机动车排放检验与维修制度(简称“I/M”制度)已进入实施阶段,目前机动车排放维修治理站使用的机动车诊断仪器的诊断工况为自由加速法,而机动车大多数工况为加载减速法,机动车诊断工况不能对应现有的检测工况,诊断准确率较低,诊断结果不可靠,导致在治理尾气超标时,无法快速找到超标的准确原因,机动车维护成本大大增加,“I/M”制度落地实施难以积极推进[1-2]。

当前,发动机故障大多利用振动信息分析,虽准确率高,但诊断结果十分依赖采集的振动信号,振动信号极易受到干扰,不适用于快速诊断[3-6]。在车辆检测诊断中,尾气的获取较简单,尾气成分及其含量数据中有大量的发动机燃烧信息,能够反映柴油机燃烧过程中的空燃比、喷油压力等变化规律。国内外专家也对基于尾气信息与人工智能算法进行了研究,但尾气的获取方法大多停留在理论研究阶段,且不适用于机动车定期排放检测[7-11]。

本文中基于神经网络算法,设计一种利用柴油车排放检测尾气信息准确诊断排放故障的柴油车尾气诊断系统,快速准确进行柴油机尾气超标故障诊断。

1 柴油车故障排放测试

1.1 排放试验设备

采用加载减速法和自由加速法对2辆不同柴油车进行排放检测,2辆车的发动机均采用增压中冷、高压共轨技术,满足国五排放标准,车辆A型号为唐骏欧铃K3系列轻卡,额定质量为1 496 kg,整备质量为4 495 kg;车辆B型号为豪沃ZZ4257N3247E1BB,整备质量为8 800 kg。2辆机动车配置的发动机主要技术参数如表1所示。

试验中的测试仪器为:1)MQW-5105(Z)气体分析仪。测量的尾气成分分别为CO、CO2、O2、NO、NO2,体积分数测量范围分别为 0～14.0%、0～18.0%、0～25.0%、0～5 000×10-6、0～500×10-6。2)MQY-202透射式烟度计,光吸收系数k测量范围为0～16.08 m-1。3)WZS04汽车通用转速仪。四缸四冲程发动机转速测量范围为360～9 000 r/min,六缸四冲程发动机转速测量范围为360～6 000 r/min。4)汽车底盘测功机。滚筒直径为370 mm,额定吸收功率为700 kW,最高车速为130 km/h,额定承载质量为13 t,基本惯性质量为1 454 kg。

故障模拟前,首先对2辆车辆进行无故障测试,保证发动机的排放控制系统正常工作,以此作为基准,模拟4种排放控制技术常见的故障:加载减速法工况下,对车辆A进行空气滤清器故障和SCR故障模拟,车辆B进行空气滤清器故障和进气软管漏气故障模拟;自由加速法工况下,车辆A进行SCR故障、喷油嘴损坏故障、空气滤清器堵塞故障模拟,车辆B进行空气滤清器堵塞故障、进气软管漏气故障模拟。

故障模拟方法为:1)将尿素与水按照体积比1：4配比添加到尿素箱中,稀释尿素的浓度,模拟SCR故障;2)断开其中一个喷油嘴电连接,使各气缸之间的燃油喷射量不一致,模拟喷油嘴损坏故障;3)用硬纸板紧紧盖住进气口,使进气不通畅,模拟空气滤清器堵塞故障;4)拔开进气软管,使进气软管处漏气,模拟进气软管漏气故障。

选择实测最大轮边功率时的转鼓线速度(记为工况1)和实测最大轮边功率时的转鼓线速度的80%(记为工况2)为试验工况。

1.2 试验结果分析

利用尾气信息对发动机进行故障诊断,不同的故障导致尾气中污染物排放体积分数发生变化,发动机排放参数对故障的敏感度用增长率表示,增长率

r=(a-b)/b,

(1)

式中:a为故障状态下排放参数结果,b为无故障状态下排放参数结果。排放参数包括测试过程中车辆的最大轮边功率、发动机额定转速、光吸收系数k、尾气中NOx的体积分数φ(NOx)。

加载减速法工况下车辆A、B对各故障的敏感度分别如表2、3所示。

由表2可知:对于轻型柴油机车,最大轮边功率能够反映车辆的动力性,车辆A空气滤清器堵塞故障和SCR故障均影响轻型柴油车的动力性,空气滤清器对最大轮边功率影响较大;车辆A空气滤清器堵塞后,k敏感度减小,且减小幅度较大;φ(NOx)敏感度很小,几乎为0。这是由于最大轮边功率降低,空气滤清器堵塞导致车辆发动机功率下降,低功率下排放性能较好。工况1下,空气滤清器故障的k敏感度大于SCR故障,即工况1下k对空气滤清器堵塞故障较敏感。车辆机外后处理系统中,SCR主要用于吸收NOx,SCR故障导致净化效率降低,大部分NOx无法转化为干净气体,直接排放到空气中,SCR故障对k的影响不大,φ(NOx)对SCR故障十分敏感。工况2下φ(NOx)敏感度达到了191.89%,k敏感度变化不大,但工况1下k敏感度呈现增加趋势,工况2下呈现降低趋势,同时车辆最大轮边功率的敏感度降低11.18%。

由表3可知:重型柴油车的空气滤清器堵塞故障和进气软管漏气影响车辆的动力性,尤其是空气滤清器堵塞,车辆最大轮边功率敏感度降低了41.45%;工况2 的k敏感度和φ(NOx)排放敏感度均增加,φ(NOx)敏感度增加95.77%,但工况1的k敏感度降低。进气软管漏气导致车辆吸气损失增大,混合器过浓。在加载减速法试验中,车辆最大轮边功率敏感度降低,同时其工况1、2的k敏感度和工况2的φ(NOx)敏感度也降低,且k敏感度降低明显。虽然空气滤清器和进气软管均为车辆进气系统部件,但车辆对2种故障的敏感度不同,空气滤清器故障对最大轮边功率的影响更敏感,进气软管漏气故障对k的影响更敏感,空气滤清器故障对φ(NOx)的影响更大,并且空气滤清器故障对φ(NOx)的敏感度为正,进气软管漏气φ(NOx)排放的敏感度为负。

表3 加载减速法工况下车辆B对各故障的敏感度

综上分析,排放参数对不同故障的敏感度不同,能够根据排放结果分析燃烧情况,因此可以将试验数据纳入神经网络数据库进行分析。

自由加速法工况下车辆A、B对各故障的敏感度及对应转速如表4、5所示。

表4 自由加速法工况下车辆A对各故障的敏感度及对应转速

表5 自由加速法工况下车辆B对各故障的敏感度及对应转速

由表4、5可知:3种故障对轻型柴油车发动机的转速影响不大,但是对重型柴油车发动机转速影响较大,空气滤清器堵塞导致发动机无法达到额定转速,最大转速仅为1 300 r/min。综合上文加载减速法分析结果,重型柴油车进气系统的零部件故障主要反映在动力性方面,其次对排放污染物也有一定的影响。

轻型柴油车的k对故障的敏感度较高,3种故障中空气滤清器堵塞对k的影响最大,增长率为72.09%;SCR故障的k敏感度降低。重型柴油车k的相对变化较稳定,这可能是因为当k达到车辆设定的数值时,限制发动机功率,这也是当空气滤清器堵塞时发动机最高转速只能为1 300 r/min的原因。

轻型柴油车φ(NOx)对故障敏感度非常高,3种故障都不同程度地影响φ(NOx),尤其是SCR故障对φ(NOx)的影响最大,φ(NOx)敏感度增长至90.99%。重型柴油车φ(NOx)对故障敏感度相对较低,2种故障中,进气软管漏气的影响较大,φ(NOx)敏感度增长至8.36%。综上,自由加速法也能够对故障车辆进行检测,可以以此获得样本数据。

经过分析得知,加载减速法试验中不同故障对最大轮边功率、工况1下的k、工况2下的k和工况2下的φ(NOx)4个参数影响不同,利用故障对排放参数影响的量化分析,可以为神经网络学习提供样本数据,同时也为神经网络仿真模型验证提供数据。

2 神经网络模型设计

2.1 GA-BP神经网络算法

BP神经网络采用反向传播学习算法调整权值和阈值,学习规则采用梯度下降法,神经网络具有输入层、隐藏层、输出层3层网络结构。

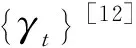
神经网络输出与期望输出误差均方差

(2)

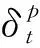
隐藏层至输出层各单元的权值修正函数

(3)

隐藏层至输出层各单元阈值修正函数

(4)

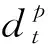
输入层至隐藏层各单元的权值修正函数

(5)

输入层至隐藏层各单元的阈值修正函数

(6)

传统BP神经网络对权值和阈值的修正仅考虑当前时刻的梯度下降,即只考虑误差的影响,而没有考虑前一时刻的梯度下降方向。

本文中将前一时刻权值和阈值的修正变量引入修正公式中,传递每次权值和阈值的变化,并且增加动量因子,调节前一时刻梯度下降对该时刻的影响。引入前一时刻修正变量后,权值和阈值调节速度缓慢下降,有助于提高收敛速度;权值和阈值向着误差最底部方向发展,有助于跳出误差曲面的局部极小值。

改进后输入层至隐藏层各单元的权值修正函数

(7)

式中mc为动量因子。

改进后输入层至隐藏层各单元的阈值修正函数

(8)

改进后隐藏层至输出层各单元权值修正函数

(9)

改进后隐藏层至输出层各单元阈值修正函数为:

(10)

引入动量项后,能够有效避免神经网络在局部极小值点修正值为0,避免陷入局部极小值。BP神经网络权值和阈值在误差曲面下降的总方向由初始的权值和阈值决定。初始权值和阈值确定多采用经验方法选取,具有不确定性,本文中增加遗传算法确定初始权值和阈值。GA-BP神经网络故障诊断算法流程为:1)获取柴油车原始尾气检测数据,并对其归一化处理,形成神经网络学习样本库。 2)利用遗传算法寻找最优的权值和阈值,并将最优的初始权值和阈值数据提供给BP神经网络,并进行训练。3)柴油机排放参数作为神经网络的输入层,故障类型作为输出层;通过隐藏层、输出层加权处理,获得输出数据,并获得输入层与隐藏层之间的权值和阈值、隐藏层与输出层之间的权值和阈值。4)利用动量项修正权值和阈值,对比当前神经网络输出与期望输出,利用式(2)计算两者的误差平方和,反向传递权值和阈值并增加动量项,根据改进后的式(3)～(10)对其修正。5)重复步骤3)和4),直到误差平方和达到设定要求。

2.2 神经网络模型设计

基于GA-BP神经网络故障诊断算法核心是将神经网络模型作为故障诊断的主要部分,利用柴油机尾气参数对不同故障的敏感度分析结果,建立神经网络模型样本集,并对该样本集进行数据预处理等,利用处理好的样本集神经网络进行训练,将训练好的网络用于故障诊断。

2.2.1 神经网络输入层设计

根据柴油车尾气参数对不同故障的敏感度可知,工况1、2的k和工况2的φ(NOx)3个参数的敏感度对研究发动机故障诊断十分有效,能够预测柴油机的故障类型和柴油机进气系统、排气系统以及燃油喷射系统的工作情况。本文将神经网络的输入数据设置为工况1、2下的k和工况2下的φ(NOx),对应的网络输入神经元数量为3。

2.2.2 输出神经元设计

选取试验中加载减速法设计的4个故障与某M站获取的某柴油车(以下称车辆C)2个故障进行分析,6种故障分别为:车辆A的空气滤清器堵塞和SCR故障,车辆B的进气软管漏气和空气滤清器堵塞故障,车辆C的进气软管漏气和喷油嘴损坏故障,用数字1～6表示。对可能存在的6个柴油机故障设置输出层神经元数为6,并且对6个故障进行数字编号,二进制编码方式如表6所示。

表6 输出神经元编码方式

2.2.3 隐藏层节点数确定

确定隐藏层数的神经元比较复杂,通常没有固定的理论支持。隐藏层数太少,网络训练不充分,隐藏层节点数太多,导致学习时间过长,甚至无法完成学习过程。

确定隐藏层节点需要借助经验公式选择,隐藏层节点数的经验公式为:

(11)

式中:N1为隐藏层节点数;N为输入层节点数;M为输出层节点数;A为常数,且1≤A≤10。

本文中输入层节点数为3,输出层节点数为6,因此设定隐藏层节点数为3～13,隐藏层节点数对应输出误差曲线如图1所示。由图1可知:隐藏层数为12时,训练集的准确率最高,因此选择隐藏层数为12。

图1 隐藏层节点数对应误差曲线

2.2.4 数据预处理

神经网络中输入数据量纲不同。本文中将工况1、2的k和工况2的φ(NOx)作为输入,并对3个输入数据采用最大值归一化处理方法进行归一化处理,输入数据区间为[0,1]。

2.3 神经网络训练及分析

根据试验数据与M站实际应用中的诊断数据,选取161组样本,其中样本数据的70%作为神经网络训练数据,30%作为神经网络测试数据。

利用MATLAB软件仿真,2种方法输入层节点均为3,输出层节点均为6,隐藏层节点数均为12。采用Tansig函数作为隐藏层传递函数,采用均方误差作为误差函数,由于输出层的参数为0或1,因此采用一次函数作为输出层传递函数,将6个输出中的最大值设置为1,其他5个输出设置为0,即可与上文二进制编码对应,获得输出值,部分输出结果如表7所示。

表7 BP神经网络部分输出结果

利用BP神经网络,设置误差函数期望误差为0.002,训练次数为1 000次,学习速率0.001,经过923次循环后,神经网络误差函数值达到目标值,误差为0.001 994 5。

利用GA算法优化BP神经网络算法,初始种群规模为50,最大迭代次数为20,交叉概率为0.8,变异概率为0.01。利用GA算法优化时,每次进化过程中的最优个体适应度如图2所示。由图2可知:迭代次数为20时,对应最佳真实适应度为0.983 702。将迭代次数为20的权值和阈值作为初始值对BP神经网络优化。

图2 适应度散点图

利用GA算法优化的GA-BP神经网络算法传递函数、目标误差参数、训练次数和学习速率设定与BP神经网络相同,增加动量因子为0.9,经过493次训练达到目标值,最终误差为0.001 993 2。

GA-BP和BP神经网络2种算法训练过程如图3所示,2种神经网络预测结果对比如图4所示。

图3 2种算法训练过程对比图 图4 2种神经网络算法预测和期望对比图

由图3可知:BP神经网络经过923次循环后,达到目标值,下降梯度越来越小,学习优化速度越来越小;GA-BP神经网络经过493次循环后,达到目标值,下降梯度没有明显减小,还可以继续学习优化,学习速度也没有明显降低。由图4可知:49组数据测试中,BP神经网络模型有4组数据预测错误,准确率为91.84%,训练时间为19 s;GA-BP神经网络模型在测试中,预测全部正确,准确度高达100%,训练时间为5 s。利用GA算法对神经网络参数优化,减少BP神经网络迭代过程,从而减少训练时间; GA算法优化效果明显,寻找到更优的权值和阈值,故障诊断准确率大大提高。

3 尾气智能诊断系统开发及实车验证

3.1 系统开发

柴油车尾气智能诊断系统包括信号采集装置和上位机软件程序,信号采集装置包括转速传感器、不透光烟度计和五气分析仪。信号采集装置用来获取车辆发动机转速、k值和排放中φ(NOx)。上位机软件程序是检测员对诊断系统日常操作的可视化界面,通过与信号采集装置通信,获取采集的信息,并进行诊断。

上位机软件程序是诊断人员诊断时日常操作的可视化界面,上位机程序在传统的车辆检测程序中,嵌入柴油车故障诊断模型,增加车辆诊断子程序。上位机程序主要包括:登录子程序、车辆登记子程序、车辆检测子程序、车辆诊断子程序。

车辆诊断程序流程如图5所示。车辆检测不合格后,提取原始的检测数据;对数据进行预处理,利用训练好的神经网络分类器通过处理过的输入数据对发动机进行故障分类诊断;得到诊断结果,并打印诊断报告;车辆维修后,获取维修人员输入的本次维修的准确的诊断报告,准确诊断报告作为神经网络分类器学习样本库中的一条样本,判断距上次更新学习后新增诊断样本数,如果没有超过100,则结束程序,如果数量超过100则进行神经网络分类器训练,训练完成后,结束程序。神经网络分类器训练程序流程如图6所示。

图5 车辆诊断流程图 图6 神经网络分类器训练程序流程图

在实际应用中,诊断出具单个故障误差较大,因此设计此系统时,出具的诊断结果为两项故障类型。输出故障时,将输出层数据由大到小排序,选取最大值和次最大值,作为故障诊断结果。故障诊断模型输出判断流程如图7所示。

图7 故障诊断模型输出判断流程图

3.2 实车试验

在实际的车辆检测中,大多数车辆应用加载减速法对车辆进行检测,只有少数车辆应用自由加速法对车辆检测,本文中选择车辆B采用加载减速法进行实车验证系统性能。为了验证系统的稳定性以及诊断性能,模拟车辆空气滤清器故障和SCR故障,针对每个故障分别对车辆进行10次加载减速法,测试本系统在20次诊断中的性能。每次车辆检测循环完成后,进行车辆诊断,记录诊断时间及诊断结果。测试完成后,对该系统进行更新,训练神经网络分类器。通过实车测试,本系统稳定运行,能够实现柴油车加载减速法检测和柴油车诊断功能。

设计的诊断系统对空气滤清器故障和SCR故障诊断时间和结果如表8所示。

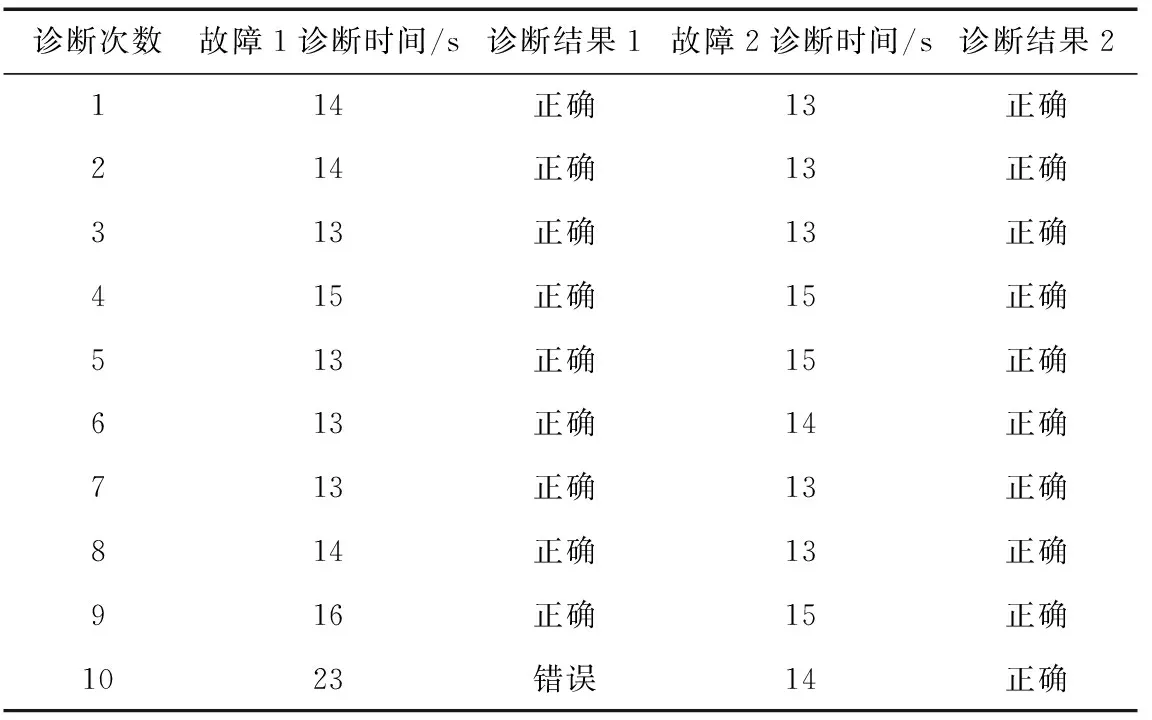
表8 柴油车尾气智能检测诊断系统性能

由表8可知:本系统能够诊断柴油车故障,诊断准确率为95%,认为该系统诊断正确;该诊断系统在20次的故障诊断中,仅在第10次空气滤清器堵塞故障诊断时,出现诊断错误,同时诊断时间也增加。本次诊断中将故障诊断为进气软管漏气,可能是因为车辆驾驶员未完全按照检测工况行驶车辆,车辆排放数据不准确,导致故障诊断错误。

20次循环诊断完成后,更新系统,重新训练柴油车故障诊断模型,实现更新功能,系统更新时间为10 min,随着样本数量的增多,系统更新时间增加。

4 结论

1)通过实车测试了柴油机部分故障对排放的影响,提出了利用加载减速法和自由加速法获取的实车检测过程尾气数据诊断柴油车排放故障。

2)建立了基于改进GA-BP神经网络的柴油车故障诊断模型,在传统的BP神经网络算法中,增加动量项和遗传算法,优化BP神经网络,诊断性能大幅提高。

3)开发了柴油车尾气智能检测诊断系统,在传统的柴油车排放检测系统中,增加故障诊断系统,将柴油车故障诊断模型嵌入故障诊断系统,实现了柴油车尾气智能检测诊断。