基于欧拉-拉格朗日方法的高压喷雾过程数值模型
余磊,肖明雅,王润涛,陈江锋,周涛涛,唐志全*
1. 安徽全柴动力股份有限公司,安徽滁州 239500;2.中国科学技术大学工程科学学院,安徽合肥 230026;3.合肥工业大学汽车与交通工程学院,安徽合肥 230009
0 引言
随着能源与环境问题日益突出,机动车污染物排放标准不断提高,2019年开始实行的国六排放标准对燃油车排放提出更加严格的要求,高效与清洁技术已经成为内燃机发展的重点方向[1-2]。燃油雾化质量是影响内燃机燃烧过程的重要因素,在很大程度上决定内燃机的动力和排放特性[3]。喷雾雾化过程是极其复杂的两相流问题,涉及到气-液两相间的相互耦合以及液滴的碰撞、破碎和蒸发等多个过程。常用的试验手段只能宏观展现燃油雾化的工作过程[4],获取的流场信息有限,数值模拟具有经济性和强大的信息获取能力,可以获得雾化过程中湍流与液滴的详细演化特征,已经成为研究喷雾发展过程的重要手段[5-6]。
模拟湍流和液相运动是喷雾雾化过程数值仿真的重点。由于直接数值模拟和大涡模拟需要巨大的计算量,目前工程应用上仍多采用Reynolds平均法(简称RANS方法)处理雾化过程中的气相湍流运动,同时耦合液滴破碎模型模拟雾化过程。万吉安[3]基于欧拉-拉格朗日方法,湍流模型采用标准k-ε模型,液滴破碎模型采用Wave模型进行柴油机燃油喷雾过程的三维数值模拟;周乃君等[7]采用标准k-ε湍流模型耦合Wave液滴破碎模型研究了各种工况下高压燃油喷射雾化过程中的喷雾贯穿距和锥角等宏观特性的发展规律;邢志海等[8]采用标准k-ε湍流模型耦合Wave液滴破碎模型对高压共轨单孔喷油器高压燃油喷雾微观特性数值模拟研究;王勇[9]采用标准k-ε湍流模型、KH-RT液滴破碎模型进行了超高压燃油雾化过程仿真研究,探讨了不同模型参数不同工况下数值模拟效果;王昆朋[10]采用RNGk-ε湍流模型耦合KH-RT液滴破碎模型探究了不同喷射压力、不同喷射策略对发动机喷雾发展和混合气形成过程的影响。虽然对喷雾雾化过程进行模拟时采用了不同的湍流模型和液滴破碎模型,但对内燃机工作过程中的高压喷雾计算,哪种模型的精度更高并无明确结论,因此有必要开展不同湍流模型和液滴破碎模型对高压喷雾过程模拟结果准确性的评估研究。
近年来,美国Sandia国家实验室下的Engine Combustion Network(ECN)研究组开展了一系列燃油喷雾试验研究,为喷雾雾化及燃烧过程的数值模拟提供了更多的标定数据,其中应用较为广泛的是以正十二烷为燃料、代号为Spray A的试验研究,这是由于正十二烷与柴油的碳链长度、沸点等性质更接近,使用正十二烷可以更准确地再现柴油喷出后的蒸发和混合过程,因此受到广大研究人员的关注[11-16]。
本文基于欧拉-拉格朗日方法,采用不同的湍流模型和液滴破碎模型对Spray A喷雾开展数值模拟研究,对比仿真与试验结果,分析不同模型对内燃机高压喷雾雾化过程模拟准确性的影响,为高压喷雾雾化过程的数值模拟研究提供参考。
1 数值模型
1.1 湍流模型
RANS方法的核心是不直接求解瞬时的Navier-Stokes (N-S) 方程,而是求解时均化的雷诺(Reynolds)方程。对流动质量、动量和能量输运方程进行Reynolds平均,构建时均输运方程。本文中不涉及气体高速流动,将流体视为不可压缩流体,故以张量表示的时均连续方程[17]和时均Reynolds方程(RANS方程)[17]为:
(1)
(2)
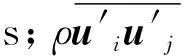
式(1)和(2)组成的方程组中未知量大于方程组数量,方程组不封闭,需要引入新的方程才能使方程组封闭。引入不同的方程则形成不同的模型。
1.1.1 Reynolds应力方程模型(RSM)
(3)
式中:Cij为对流项,DT,ij为湍流扩散项,DL,ij为分子黏性扩散项,Pij为剪应力产生项,Gij为浮升力产生项,φij为压力应变项,εij为黏性耗散项,Fij为系统旋转产生项。
雷诺应力模型是对湍流流动最完整的物理表示,可以直接模拟RANS方程中的流动项,适用于强旋转和流线曲率造成的湍流稳定性等非常复杂的流动问题。
1.1.2k-ε模型
在标准k-ε模型中,关于湍动能k的输运方程[17]为:
(4)
式中:μt为湍动黏度,μt=ρCμk2/ε,其中Cμ为经验常数;Prk为k对应的普朗特数;Gk为由平均速度梯度引起的k的产生项;Gb为由浮升力引起的k的产生项;YM为可压缩湍流中的脉动扩张项;Sk为用户定义的关于k的源项。
关于湍流耗散率ε的输运方程[17]为:
(5)
式中:C1ε、C2ε、C3ε是由研究经验得出的常数;Prε为ε对应的普朗特数;Sε为用户定义的关于ε的源项。
为了弥补标准k-ε模型的不足,科研人员提出了适用不同情况的RNGk-ε模型[18]、Realizablek-ε模型[19]。RNGk-ε模型中对湍流黏度进行了修改,解决了标准k-ε模型对于旋转流动、强曲率流动计算失真的问题。Realizablek-ε模型将湍流黏度计算中的Cμ与应变率相联系。该模型适用于高压射流、剪切流、大曲率流动,并且强化了分离与强压差流动界层的性能。
1.1.3k-ω模型
标准k-ω模型中,对应的湍动能k的输运方程[17]为:
(6)
式中:Γk为k的扩散顶,Yk为k在湍流下的耗散。
湍流耗散率ω的输运方程为:
(7)
式中:Gω为ω产生项;Γω为ω的扩散率,Yω为ω在湍流下的耗散,Sω为源项。
相比k-ε模型,k-ω模型可以更好地模拟壁面附近的流动,而且能够很好地模拟逆压梯度边界层流动和分离。但是该模型不能准确模拟自然流,对于逆压梯度造成的剪切力预测过高。相比于标准k-ω模型,通常建议选用改进的SSTk-ω模型[20]。改进的SSTk-ω模型以壁面距离为基准,在壁面近场使用k-ω模型,在壁面远场采用k-ε模型,更好地结合k-ε和k-ω模型的优点。
1.2 离散相模型
喷雾过程包含液滴的喷射、破碎等复杂过程,均需要相应的模型进行模化[21]。本文中以离散相模型 (discrete phase model,DPM) 对液滴的位置、质量、动量以及温度进行追踪求解。
弛豫时间[17]
(8)
式中:dp为液滴颗粒直径,m;Re为相对雷诺数;CD为曳力系数。
笛卡尔坐标系下x方向的离散相液滴的作用力平衡方程[17]为:
(9)
式中:u为流体速度,m/s;uP为液滴的速度,m/s;gx为液滴在x方向的加速度,m/s2;ρp为液滴密度,kg/m3;Fx为液滴受到的其他力的作用,包括热致迁移力、布朗力、萨夫曼升力等,本文中只考虑虚拟质量力即使颗粒周围流体加速引起的附加作用力、压力梯度力的作用。
虚拟质量力[17]
(10)
压力梯度力[17]
(11)
考虑瞬时湍流速度脉动对颗粒轨迹的影响,对离散相颗粒的分布采用随机轨道模型。在实际过程中,通过连续相的差得到液滴所需要的流动信息。
1.3 液滴破碎模型
由于高压喷雾雾化过程中韦伯数较高,故选用Wave Breakup Model(简称Wave模型)、KH-RT Breakup Model(简称KH-RT模型)、Stochastic Secondary Droplet Model(简称SSD模型) 3种适用于高韦伯数流场的液滴破碎模型进行分析。
1.3.1 Wave模型
基于圆柱射流稳定性的线性分析,研究人员建立了Wave破碎模型[22]。圆柱射流在环境气体中受到的小扰动
η=η0exp(inz+wt),
(12)
式中:η0为初始振幅,n为波数,z为流动方向,w为波的增长率。
基于小扰动假设,对控制射流柱运动的N-S方程进行线性化处理,代入边界条件可得到色散方程。拟合色散方程的解,可得表面波的最大增长速率的方程[22]为:
(13)

表面波的波长方程为:
(14)
式中:ΛKH为增长最快表面波的波长,m。
Wave破碎模型认为射流柱表面气液间剪切力的作用使射流柱出现了不稳定性,即KH表面波引起了射流表面的不稳定性,并最终导致了子液滴从射流柱表面剥落。因此,Wave破碎模型也称为KH破碎模型。
液滴破碎后的子液滴半径[22]
(15)
式中:B0为模型常数,本文中B0=0.61。
关于母液滴的半径表达式[22]为:
(16)
式中:tKH为KH波破碎时间,tKH=3.726B1r/ΛKHΩKH,其中,B1为与喷嘴结构、喷嘴内部流动状态有关的模型常数,常取1.7~60.0,本文中B1=9.0。
1.3.2 KH-RT模型
KH-RT模型认为液滴的破碎不仅是因为KH表面波的扰动,还有另一种不稳定波的扰动,即RT表面波。RT模型认为扰动是在高速射流的气液交界面上由密度差导致液相向气相加速而引起的。与KH模型类似,RT模型也是根据增长率最高的波的波长来决定液滴的破碎方式与破碎时间。虽然KH-RT模型中的KH波与RT波共同控制液滴破碎,但两者之间存在一定的竞争关系。在喷雾近场,由于射流内部接触的气体很少,所以KH波对液滴的破碎起主要作用;在喷雾远场,液滴与环境气体直接接触,首先在RT模型中,由液滴的破碎特征时间是否大于RT破碎时间决定液滴是否发生破碎,其次在KH模型中,由液滴韦伯数是否大于临界韦伯数判断是否发生KH破碎,临界韦伯数设为12。
KH波最大增长率ΩKH、相应波长ΛKH及破碎时间表达式在KH破碎模型中已描述,KH-RT模型中B0=0.61,B1=60。
RT波最大增长率ΩRT、相应波长ΛRT、破碎时间tRT以及子液滴半径rchild的表达式[22]分别为:
(17)
ΛRT=2πCRT/KRT,
(18)
tRT=Cτ/ΩRT,
(19)
rchild=πCRT/KRT,
(20)
式中:gt为液滴行进方向上的加速度,m/s2;CRT为破碎半径常数,CRT=1;Cτ为破碎时间常数,Cτ=0.5。
1.3.3 SSD模型
SSD模型将液滴破裂视为一种离散的随机事件导致直径尺度在一定范围内的分布。在SSD模型中,液滴破裂的概率与母液滴和次级液滴的大小无关。破裂模型可预测发生破裂的时间以及新液滴的数量和属性。液滴半径大于临界半径rcr时液滴发生破裂。
临界半径[17]
(21)
式中:Wecr为临界韦伯数,本文中Wecr=6。
破碎时间[17]
(22)
式中:B为破碎常数,B=4。半径大于临界半径的液滴的破裂时间会增大,当液滴上的破裂时间大于临界破裂时间时,发生破裂。
当一个液滴破碎时,这个液滴破碎成数个新的包裹。包裹中颗粒的半径通过对数分布函数随机获取[17]。
液滴发生分解时,创建足够多的小包裹,使每个小包裹所代表的液滴数大致等于所设置的小包裹目标数Np,本文中Np=1 000。
1.4 物理模型及计算条件
喷雾过程示意如图1所示。由图1可知:喷雾的物理过程大致可分为喷嘴孔内流动、喷雾近场的初次雾化、喷雾远场的二次雾化3个阶段。这3个阶段中包含以下几方面的复杂过程:液柱流动、分裂形成液滴;液滴进一步破碎、碰撞、聚合、再破碎;液相蒸发、与环境气体混合以及液相与气相的相互作用等,使得喷雾过程的模拟计算十分复杂。
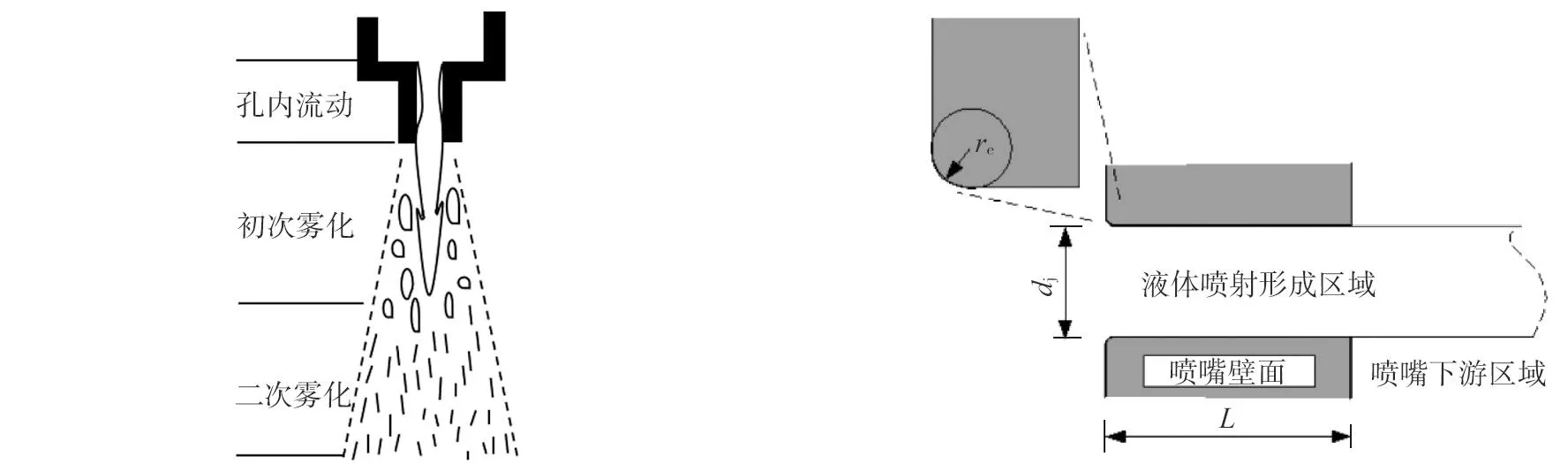
图1 喷雾过程示意图 图2 平口喷嘴结构
Spray A喷雾试验中使用单孔共轨喷油器,数值模拟选用平口雾化喷嘴模型,平口雾化喷嘴模型结构如图2所示,喷嘴结构参数孔板长度L=0.1 mm,喷射器内直径dj=0.09 mm,拐角曲率半径re=0.001 mm。
为简化计算,将喷雾过程近似看作一个空间对称的物理过程,可进一步简化为二维旋转对称的物理过程。参考Omidvar等[23]的数值计算方法,建立二维对称计算域,计算网格如图3所示,其中,对网格以喷口为中心采用横向和纵向的渐进加密,网格的长和宽分别为80、40 mm,网格数为800×400个,O(0,0)处为喷嘴位置;边界1为恒温壁面边界,边界2为压力出口边界。本文中数值模拟基于Spray A试验,基本参数采用Spray A的计算工况的参数,如表1所示。

表1 Spray A计算工况相关参数

a)局部放大 b)计算网格图3 Spray A计算网格
1.5 网格无关性分析
为了保证获得的结果不受网格质量影响,对网格进行无关性验证,选用标准k-ε湍流模型耦合Wave破碎模型进行验证,网格数量分别为20.6万、32.0万,40.5万。以y=0中轴线上的1.5 ms时气相流场的速度计算结果作为对比,不同网格数量下的y=0中轴线x方向不同位置处气相流场速度曲线如图4所示。由图4可知:除气相流场峰值速度外,3个网格的速度基本相同;网格数量为32.0万时气相流场的峰值速度与40.5万时的峰值速度几乎一致,但是网格数量为20.6万时气相流场的峰值速度明显较小,说明网格数量为32.0万时的网格精度可以满足计算要求,即满足网格无关性。因此,本文中的计算采用网格数量为32.0万的网格。
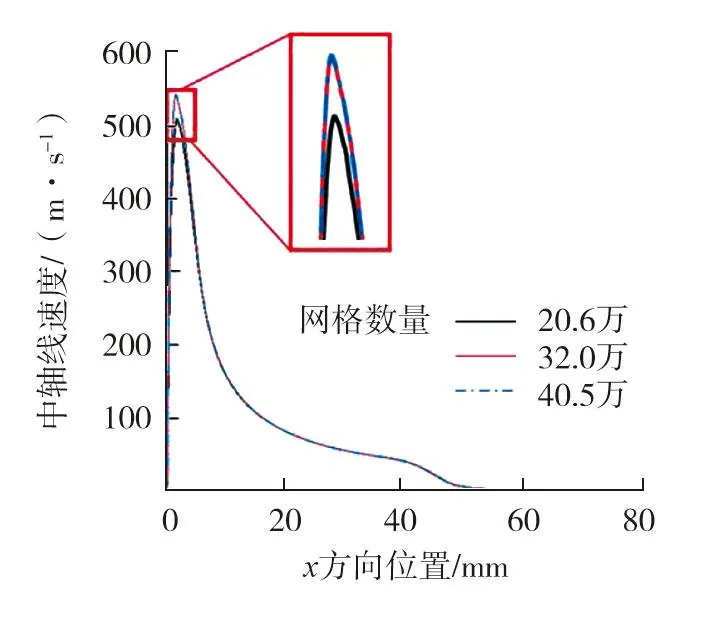
图4 不同网格数量时中轴线x方向不同位置处气相流场速度对比图
2 仿真结果及分析
2.1 湍流模型对仿真结果的影响分析
通过标准k-ε、RNGk-ε、Realizablek-ε、SSTk-ω以及RSM 5种湍流模型耦合Wave破碎模型对Spray A喷雾雾化过程进行模拟计算,分析不同湍流模型对数值结果准确性的影响,将5种湍流模型的仿真结果和试验结果进行对比,不同湍流模型对液相贯穿距的仿真结果如图5所示。

图5 试验和不同湍流模型对液相贯穿距的预测结果
由图5可知:不同湍流模型预测的液相贯穿距发展趋势基本与试验结果一致,都是先快速增长,而后液相贯穿距在10 mm附近上下波动;但RNGk-ε和RSM模型仿真的液相贯穿距比试验偏大的比例较大,这是由于模型对喷雾场中的湍动能预测偏小,流场的主流速度较大,使得液相轴向运动距离更远;5种湍流模型中,标准k-ε模型对液相贯穿距模拟结果的稳定性最好,随时间的波动最小。
不同湍流模型对气相贯穿距的预测结果和试验结果对比如图6所示。由图6可知:5种模型计算的喷雾气相贯穿距均偏小,但Realizablek-ε模型的仿真结果最接近试验结果,其次是标准k-ε模型,RNGk-ε模型的误差最大。
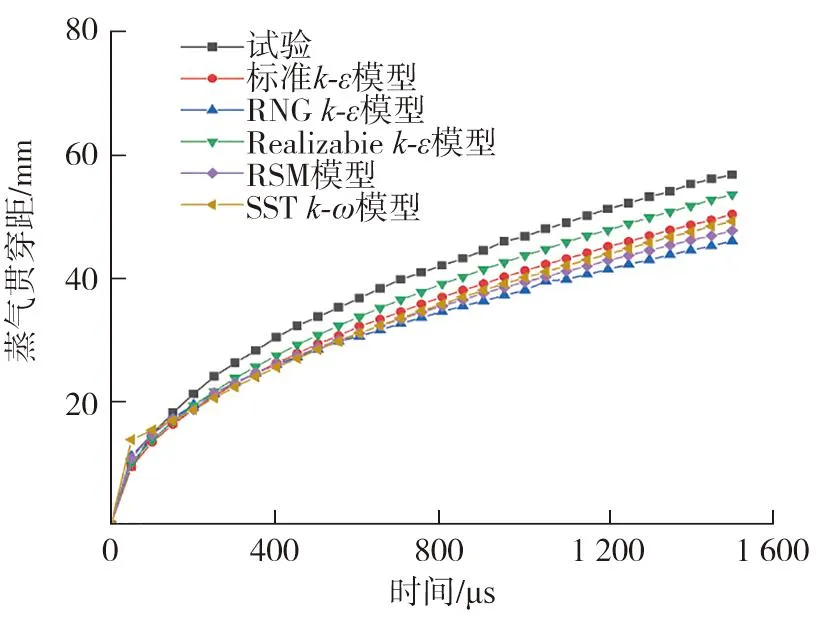
图6 不同湍流模型对气相贯穿距的预测结果和试验结果对比
不同时刻喷雾形态试验结果及不同湍流模型仿真结果如图7~12所示,其中白色点划线表示喷雾轴向到达的最远位置。由图7~12可知:仿真得到的喷雾形态与试验图像大致相同。仿真图像与试验图像的差异主要表现在2方面:1)试验图像的边界轮廓粗糙不平,仿真图像边界轮廓光滑平整,这是由于实际情况下液滴与连续相的湍流强相互作用形成喷雾的非对称结构,从而导致喷雾蒸气边缘粗糙不平,而5种湍流模型得到的是喷雾流场的湍流平均信息,形成了喷雾结构沿中心轴线成近似轴对称形状;2)模拟计算的喷雾蒸气发展一直慢于实际情况。Realizablek-ε模型计算的气相纵向发展最接近试验数据,与图6中的喷雾气相贯穿距一致;但从喷雾气相径向发展来看,SSTk-ω模型仿真结果更接近试验,RNGk-ε模型得到的蒸气形态存在一定程度的失真,主要表现在喷雾近场径向发展过慢,喷雾远场径向发展过快。

a)经过64 μs b)经过106 μs c)经过298 μs d)经过510 μs e)经过808 μs图7 气相喷雾形态演变过程试验结果
不同湍流模型对气相喷雾锥角的预测结果如表2所示。由表2可知:5种湍流模型的仿真结果与试验结果都存在一定的误差,但是SSTk-ω模型的气相喷雾锥角与试验结果的误差较小,其次是标准k-ε模型, RNGk-ε模型的误差最大,与气相喷雾形态演变过程的径向发展结果相同。
综上,Realizablek-ε模型在喷雾贯穿距、气相发展的仿真结果与试验结果最接近, RNGk-ε模型在所有结果的预测中误差都相对较大。在Lu等[21]的研究中也发现,RNGk-ε模型不能准确求解大体积运动,对喷雾体内气流速度的预测不合理,结合本文的结果说明此模型不适合Spray A条件下的高压喷雾仿真计算。虽然RSM模型能够较准确地预测喷雾体径向发展,但轴向发展的误差相对较大,而且RSM模型需要求解的方程较多,计算时间较长,对网格质量要求较高,所以也不建议采用RSM模型进行喷雾模拟。虽然SSTk-ω模型在喷雾体径向发展的预测略优于其他模型,但在对液相贯穿距的预测不如标准k-ε模型,对蒸气的发展预测不如Realizablek-ε模型,也不推荐使用。标准k-ε模型和Realizablek-ε模型的预测准确性都比较高,如果想获得更准确的液相贯穿距,优先选用标准k-ε模型;如果想获得更准确的气相贯穿距,优先选用Realizablek-ε模型。
2.2 液滴破碎模型对仿真结果的影响分析
通过标准k-ε模型结合不同破碎模型进行仿真,试验和不同破碎模型对喷雾贯穿距的预测结果如图13所示。
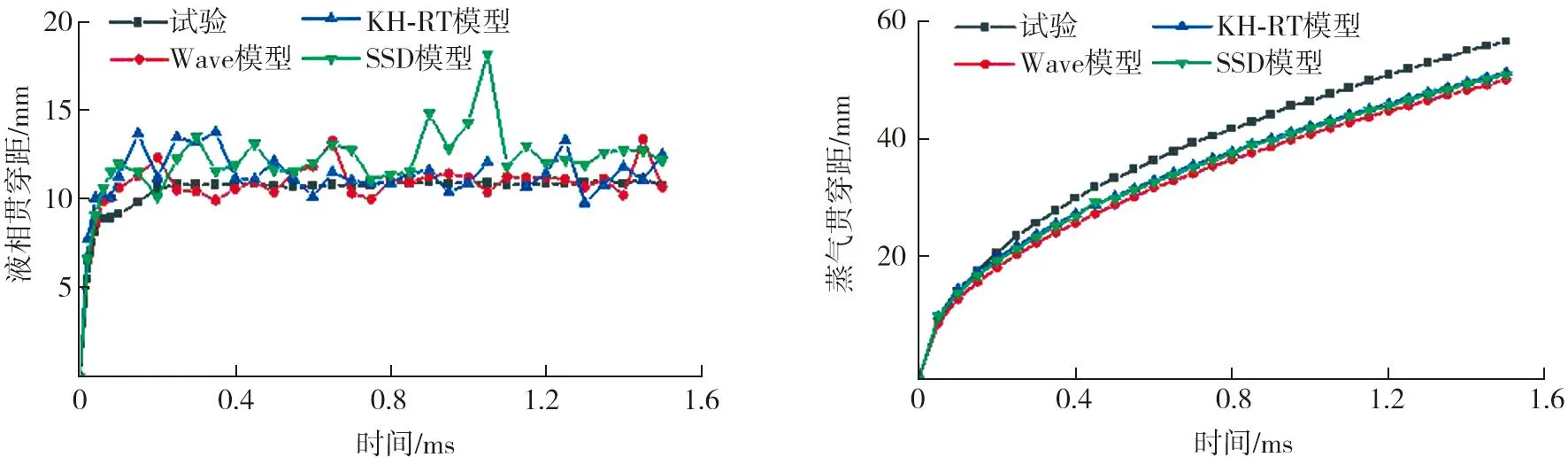
a)液相贯穿距 b)气相贯穿距图13 试验和不同破碎模型对喷雾贯穿距的预测结果
由图13可知:Wave模型与KH-RT模型计算得到的液相贯穿距与试验结果相对接近,SSD模型的预测结果相对偏大;不同破碎模型的气相贯穿距预测变化规律都与试验结果一致,但KH-RT模型和SSD模型预测的气相贯穿距相比Wave模型更接近试验结果。由于SSD模型中的液滴破碎是离散随机过程,液滴破碎的概率与液滴大小无关,导致部分液滴粒径过大,液滴获得的动量过大,轴向运动距离偏大,即液相贯穿距偏大。
不同破碎模型对气相喷雾形态演变过程的预测结果如图14~17所示,图中白色点划线表示喷雾轴向发展的最远位置。不同破碎模型对气相喷雾锥角的预测结果如表3所示。由图14~17可知:3种破碎模型计算得到的喷雾轮廓形态与试验结果基本相似,喷雾的径向发展情况与试验结果吻合良好,轴向发展与试验结果存在一定差异。结合图13中气相贯穿距以及表3蒸气锥角的仿真结果,KH-RT模型计算结果最接近试验结果,其次是Wave模型,SSD模型计算得到的蒸气形态在喷雾近场不连续,这是由于SSD模型模拟的液滴粒径较大,液滴蒸发速度慢,因此喷雾蒸气在根部出现间断。

表3 不同破碎模型对气相喷雾锥角的预测结果

a)经过64 μs b)经过106 μs c)经过298 μs d)经过510 μs e)经过808 μs图14 气相喷雾形态演变过程试验结果
由于SSD模型对喷雾蒸气形态的预测存在根部间断现象,所以SSD模型不适用于高压喷雾过程的模拟研究;KH-RT模型在液相贯穿距的预测上与Wave模型的预测结果相差不多,但在气相贯穿距和气相喷雾锥角的预测都优于Wave模型。所以,在对高压喷雾雾化过程中的数值计算中破碎模型应优先选择KH-RT模型。
3 结论
基于欧拉-拉格朗日方法,在不同湍流模型以及液滴破碎模型下对Spray A条件下的喷雾雾化过程进行仿真研究,通过对比得到高压喷雾雾化过程数值模拟研究中相对合适的湍流模型以及液滴破碎模型。
1)5种湍流模型中,RNGk-ε、SSTk-ω以及RSM模型预测的液相贯穿距和气相贯穿距与试验结果都相差比较大,这3种湍流模型不适合应用于高压喷雾雾化过程模拟研究;标准k-ε模型与Realizablek-ε模型的模拟结果与试验比较吻合,在喷雾液相贯穿距的预测中,标准k-ε模型的仿真结果更好,在气相贯穿距的预测中,Realizablek-ε模型的仿真结果更好,这两种模型都比较适合应用于高压喷雾雾化过程数值模拟研究。
2)SSD模型预测的液相贯穿对比试验结果明显偏大,而且对喷雾蒸气形态的预测存在根部间断现象,不适用于高压喷雾雾化过程的模拟研究;KH-RT模型与Wave模型的模拟结果与试验结果都比较接近,但是KH-RT模型的模拟结果准确性更高。

