导数与函数图象

杜军利

【摘  要】  本文从导数的实际意义、单调性、极值点三个角度出发，结合高考真题，阐述导数问题在高考中是如何考查的.通过针对性的甄别函数图象的练习，提升我们对导数问题的进一步认识.

【关键词】  导数；单调性；极值点

导数是研究函数的性质与形态的一个强有力的工具，在解决函数的单调性问题，求函数的极值、最值问题时应用极为方便．而根据函数的以上性质我们很容易作出函数的简图．纵观近几年高考试题，各地高考试卷中对这方面的考查是层出不穷．

1  导数的实际意义

导数反映了函数在定义域内每一点处的变化快慢程度．

例1  （2008全国卷Ⅰ）汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程看作时间的函数，其图象可能是（详情见图1）（   ）

分析  汽车的行驶路程s是时间t的函数，在经历启动、加速行驶、匀速行驶、减速行驶之后停车，其行驶速度经历由小变大，速度不变，由大变小的变化趋势，由此结合图象，选择（A）．

2  单调性的判断

对于可导连续函数来说，在某一区间则函数在该区间单调递减，反之，函数在该区间单调递增．

例2  （2008山东卷）函数的图象是（详情见图2）（   ）

分析  首先，可以判断出所给函数是偶函数，所以排除（B）（D）．其次，所给函数的导函数，而在上所以在该区间上原函数单调递增，同理，在上原函数单调递减．所以选择（A）．

3  极值点的判断

函数在某点处的导数值且在左右两侧的单调性相异，则是函数的极值点．反之，若只有则不是函数的极值点．

例3  （2006天津卷）函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点（详情见图3）（   ）

（A）1个.           （B）2个.

（C）3个.           （D）4个.

分析  函数的定义域为开区间，导函数在内的图象如图3所示，可以看出在区间内，有三个变号零点，其中只有一个零点对应的函数值，左负右正，即函数在开区间内极小值点有且只有1个，故选（A）．

4  针对性训练

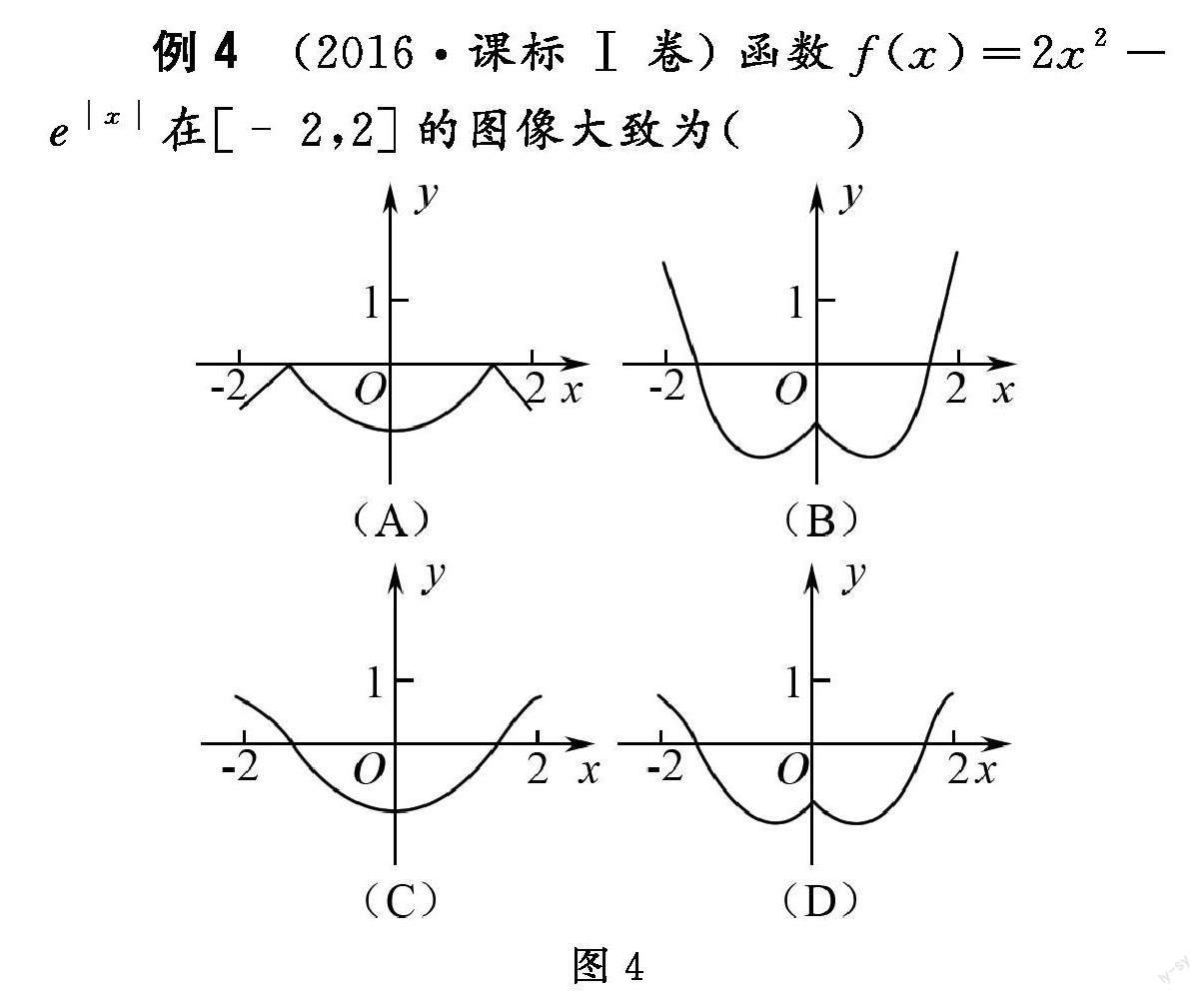
例4  已知函数y=f（x），其导函数的图象如图4，则（   ）

（A）在区间内递减.    （B）在处取得最大值.

（C）在区间内递减.    （D）在处取得最小值.

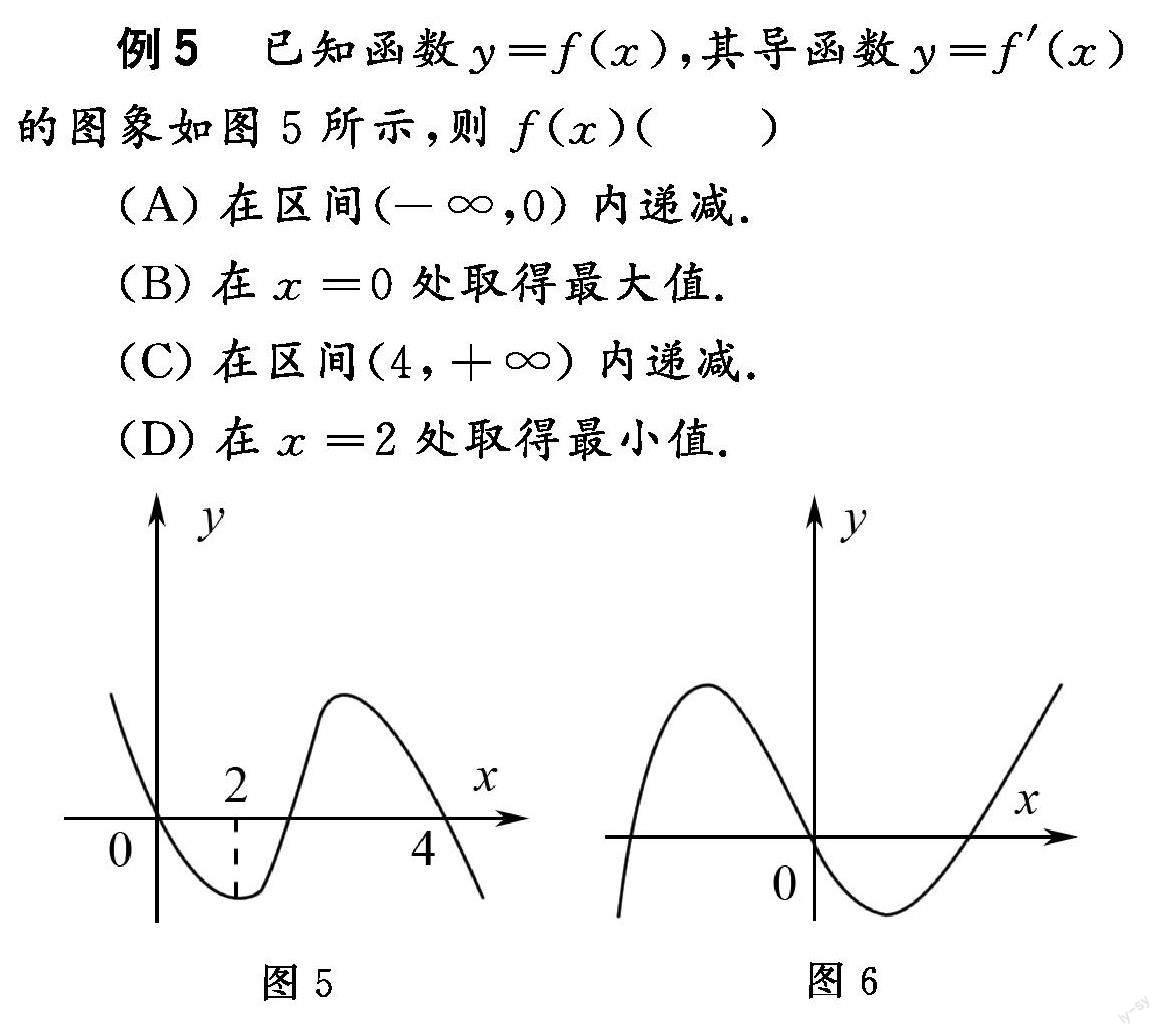
例5  已知函数的图象如图5所示，那么（详情见图5）（   ）

（A）.   （B）.

（C）.   （D）.

例6  若函数的图象的顶点在第四象限，则函数的图象是（详情见图6）（   ）

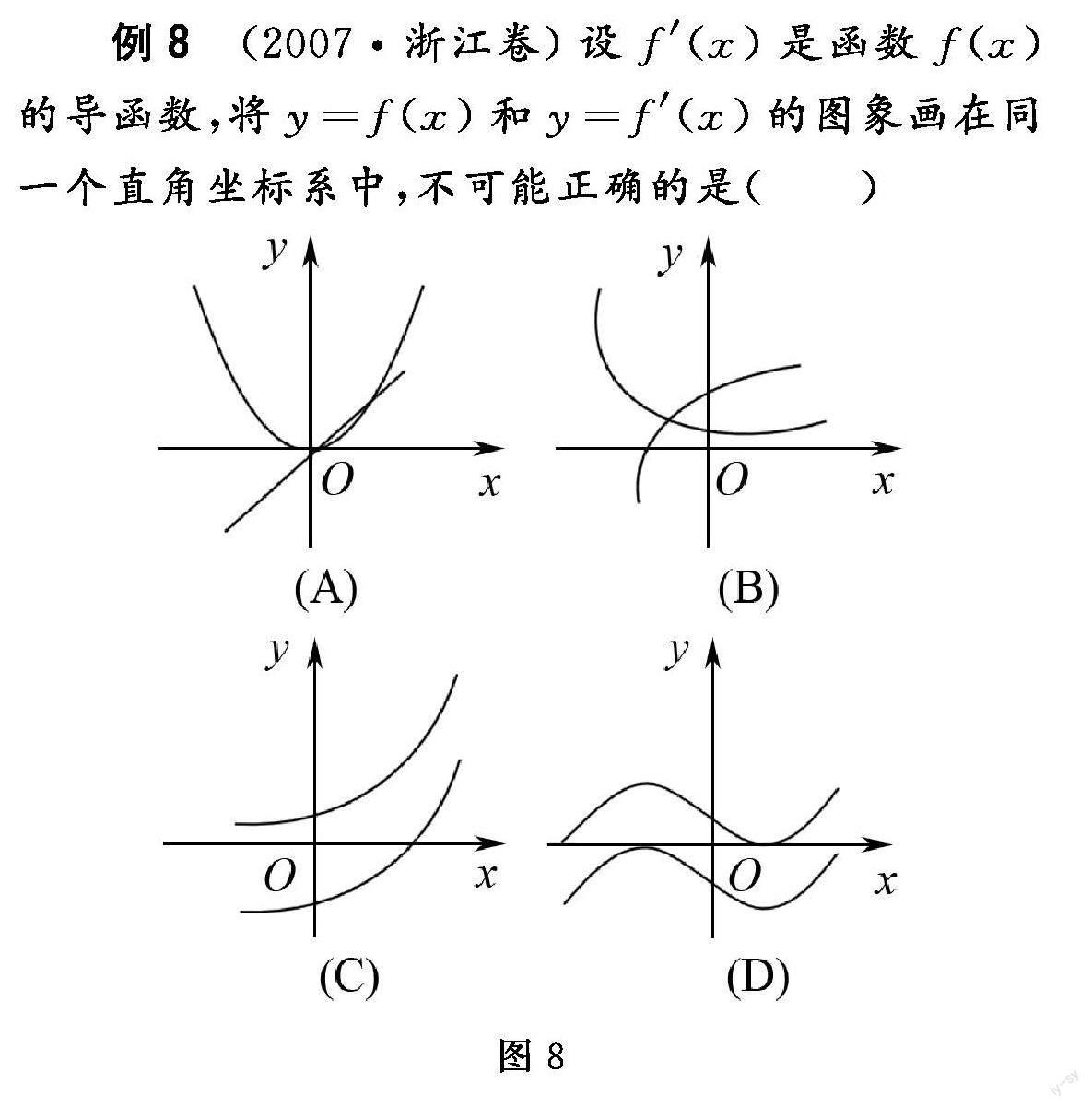
例7  （2007浙江卷）设是函数的导函数，将和的图象画在同一个直角坐标系中，不可能正确的是（详情见图7）（   ）

例8  （2005江西卷）已知函数的图象如图所示（其中是函数的导函数），的图象大致是（详情见图8）（   ）

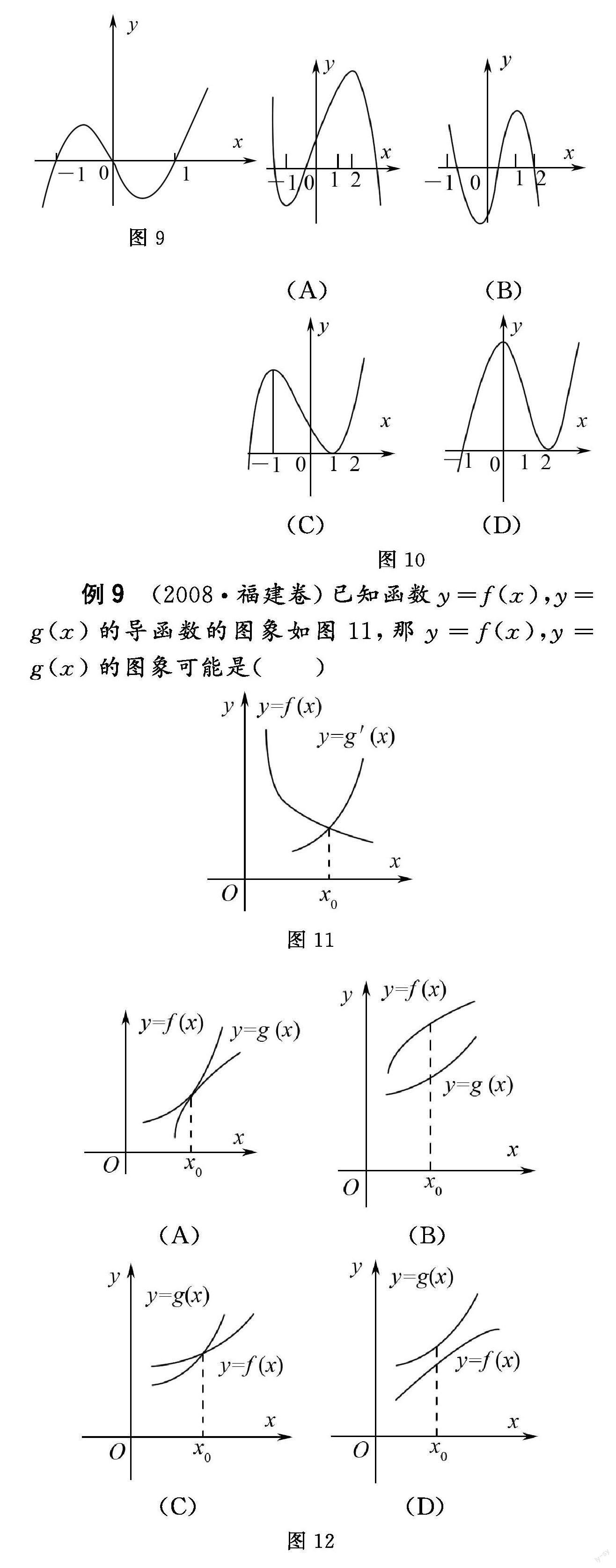
例9  （2008福建卷12）已知函數，的导函数的图象如下图，那，的图象可能是（详情见图9）（   ）

5  结语

总之，近年来高考函数图象题虽然变化很多，但不管怎么考，万变不离其宗，都是通过函数图象的“形”的特点，来间接考查函数的相关性质．综合以上分析，这类问题的解题策略简单地概括为：看图象，运用导数，看函数性质（单调性、奇偶性、对称性、极值、最值等）．灵活地运用这些解题策略，就能作出正确的判断和选择．