双光源干涉法测量液态薄膜厚度

刘维慧,梁润泽,赵泉昕,卓朝博,苗永平*

(1.山东科技大学 电子信息工程学院,山东 青岛 266510;2.山东大学 晶体材料国家重点实验室新一代半导体材料研究院,山东 济南 250100)

近几十年来,镀膜技术发展迅猛,微米、纳米级别薄膜的制造工艺日渐成熟,推动了薄膜的应用。对于如何准确测量薄膜厚度参量得到人们的广泛关注。因液态薄膜易破碎及纳米级别厚度测量精度的要求,光学干涉法在液态薄膜厚度的测量中显现出独有的优势。

以迈克尔逊干涉仪为基础,可以通过选择光源进行研究,比如利用激光外差干涉技术进行薄膜厚度测量,以精密位移平台为扫描机构可以实现薄膜厚度的逐行扫描[1];也可将经过准直系统的白光直接照射到薄膜上,通过对干涉条纹形状、分布的分析计算出薄膜的厚度[2];也可改变测量方法,比如将光学干涉原理与色度学相结合,通过计算机仿真白光干涉图进而还原薄膜厚度信息等[3-4];通过观察放入薄膜前后中央亮条纹的位置变化,反推出薄膜的厚度[5-7]等方法。目前,国内外学者对薄膜的测量主要局限于肉眼观测,虽然在一定程度上降低了测量成本,但是测量稳定性有待进一步提升,不适于工程应用;有些技术方案在理论上是可行的,但在实际测量中存在以下两个困难:(1)仪器调节复杂,耗时长,难以高效地得到清晰的白光干涉条纹;(2)依靠肉眼估算分析干涉图样,难以保证测量结果的准确度和稳定性。针对上述光学干涉法在实际应用中存在的困难,本文对基于光学干涉法的液态薄膜厚度测量技术展开深入研究和实验。

1 技术原理和调试方案

迈克尔逊干涉仪是一种利用分振幅法产生双光束以实现干涉的高精密光学仪器,通过调整全反镜的位置、角度、形状以改变空气虚膜的状态,进而实现各种类型的干涉。迈克尔逊干涉仪能将微小距离变化转化为直观可视的干涉条纹变化,因此在测量技术等方面中有着广泛的应用[8-10]。

本研究基于迈克尔逊干涉原理,综合考虑液态薄膜维持时间短、易破碎的特点,制定了其厚度测量技术方案和工作流程,如图1和2所示。

图1 光学干涉法测厚技术原理图

图2 薄膜测厚工作流程图

首先利用迈克尔逊干涉仪产生等厚干涉条纹,并确定中央亮条纹为基准条纹;随后在某一光路放入待测液态薄膜样品,并标定基准条纹的位置为初始位置;移除薄膜,干涉条纹发生变化,基准条纹的初始位置因两光束光程差的变化而移动至末态位置;最后移动动臂调整全反镜的位置以补偿光程差的变化,使基准条纹从末态位置回到初始位置;测量液态薄膜的折射率,并根据全反镜的移动距离,便可计算得到薄膜的厚度。

设薄膜折射率为n,薄膜厚度为l,则薄膜插入前后带来光程差的变化量为

δ=2(n-1)·l。

(1)

设全反镜移动距离为x,则因全反镜移动带来的光程差变化量为

δ′=2Δx。

(2)

根据上述原理,可得:

2(n-1)·l=2Δx,

(3)

则有:

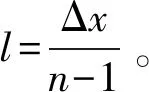
(4)

若能测得薄膜的折射率n和全反镜移动距离x,则可求得薄膜的厚度l。

1.1 干涉条纹的调试方法

只有当光束的相干长度大于两光束产生的光程差时,两光束才能发生干涉[11]。已知光的波长范围为λ～λ+Δλ时,则光束的相干长度Lc为

(5)

由式(5)可计算得到白光的相干长度约为400 nm,此长度远小于迈克尔逊干涉仪两光路之间光程差的最大范围(厘米级),故很难获得白光干涉条纹。激光具有极好的相干性和极长的相干长度,能够比较容易获得干涉条纹,但因为激光多为单一颜色,在调节时无法准确辨别基准条纹的位置变化,也就不能计算全反镜的移动距离,从而无法测量薄膜厚度。由于上述原因,液态薄膜厚度测量技术中迈克尔逊干涉条纹的调试成为技术瓶颈。

本文提出一种“激光+白光”混合调试方法,即将调试分为两步,首先使用激光作为光源,利用其相干长度大的特点进行粗调,搜索两束光产生干涉的大概区域,再切换白光光源,通过微调得到清晰的彩色干涉条纹。

图3 不同厚度空气劈尖对应的干涉条纹形状

其次进行细调。粗调完成后,两束光的光程差范围收紧在白光相干长度范围内,将光源更换为白光,使用仪器的微调旋钮可得到清晰的彩色干涉直条纹,如图4所示。

图4 白光光源的迈克尔逊干涉仪劈尖等厚干涉条纹

基于此,可知薄膜厚度不应超过白光的相干长度,在后续实验中发现,厚度在2 μm以下的薄膜,有较为良好的测量效果。

1.2 全反镜移动距离Δx的测量

在全反镜M2调节过程中,一般采用目视估算法判断所选取的基线条纹是否重合,若重合则停止调试,并读取全反镜M2移动的距离Δx;反之则继续调试,直至重合。与其他目视法一样,目视估算法存在一定的误差。为减小测量误差,本文引入基于Python的图像处理技术[12],自主开发算法,通过图像分析获取目标干涉条纹的基线并进行比对、计算基线重合度,得到全反镜M2的移动距离。

1.2.1 基本工作流程

工作流程如图5所示。

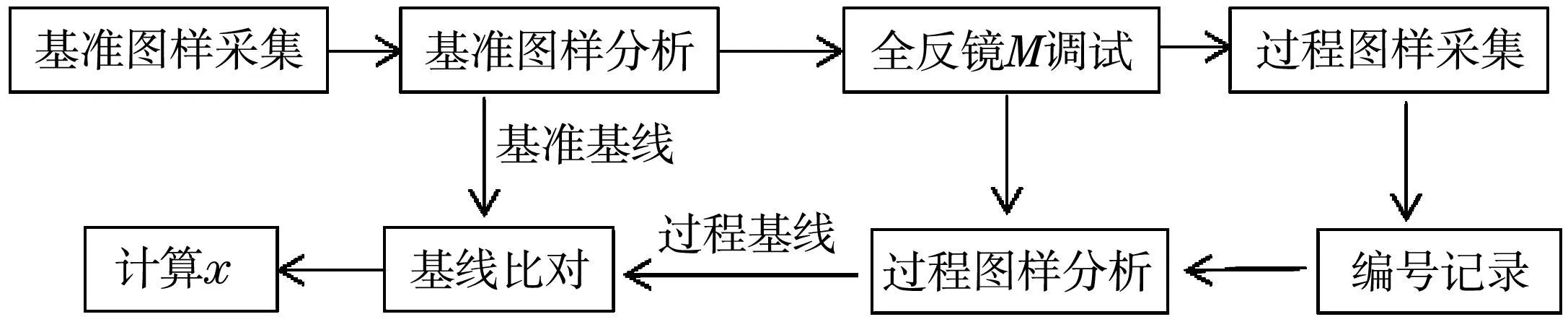
图5 基本工作流程

首先对放置液态薄膜并调试得到的清晰彩色干涉条纹图样P0进行采集,然后输入python程序进行图像分析,获得基准基线L0;移除薄膜,持续单方向按照一定步长调节全反镜,并采集过程图样,第i幅记为Pi,再逐幅分析获得过程基线,第i幅图样的基线记为Li;最后进行基线比对,选择与目标基线重合度最高的过程基线,其对应位置即为全反镜M2移动的最终位置。根据图样编号可确定全反镜的移动距离Δx。

1.2.2 图像分析

采集到彩色干涉图样后,需要对其进行分析,将采集到的图样照片中的条纹,以像素点的形式提取,并拟合为直线,作为基准或者过程基线。这是整个流程最重要的部分,基线的准确度直接影响薄膜厚度的最终结果。分析过程如图6所示。

图6 图像分析流程图

首先是图样中亮条纹坐标点的提取。通过深入研究色彩学的理论知识和图像处理算法,确定采用矢量参数HSV(即色调、饱和度、明度)模型表达彩色干涉图样信息。考虑到每次拍摄光线存在细微差距,在不同实验组中零级明条纹的颜色有一定明暗浮动,因此开发程序手动检测并确定条纹的像素参数及范围,利用cvtcolor函数计算出人工干预所选中位置的HSV值并提取对应的坐标点。最终,得到特定HSV范围内的坐标点集。

其次是像素点除杂。由于拍摄道具、图片处理等不可控因素影响,提取的像素点中存在一些离群点干扰。因此,在得到亮条纹的坐标点集后还要进行除杂处理。考虑到明条纹像素点的明度呈中间大、两边逐渐变小的分布规律,即近似正态分布。基于此,从高明度像素点的分布密度出发设计出低密度除杂算法,对分布密度较低的像素点予以剔除。

然后进行坐标点聚类筛选。由于干涉图样中存在与中央明纹HSV值相近的多条明纹,因此还需要予以清除。通过选用凝聚型层次聚类并保留数量最多的一类,来找到中央明纹对应的点集。

最后提取所保留点集的边缘点并拟合基线。由于点集存在一定的密度差异,会导致采用全部点拟合的直线存在偏差,计算量也比较大。因此,采用Gift wrapping算法对保留点集的二值图进行边缘检测。假设平面内共有n个点,对点Gi(0<=i<=n),从最左边的点i=0开始,遍历所有的点,找到点Gi+1,使得剩下的n-2个点全部在直线GiGi+1的右边,重复这一过程直到回到点G0。保留符合此算法要求的所有点,即为边缘点集。最后利用最小二乘法进行线性拟合,得到一条直线,该直线即为所采集彩色干涉图像的基线。

1.2.3 过程图样采集与编号

为了提高调试效率,按照调试-采集-分析的步骤进行。全反镜M2以固定步长Δx0单方向移动,每移动一次,采集一次图样,并按顺序编号记录、保存。全部过程图样采集结束以后,按照上节所述方法和步骤逐幅分析,得到每幅过程图样的基线。根据图样的编号可反查某幅图样所对应的动镜位置。

1.2.4 基线比对

取目标基线与坐标上下边界两点的中点,过该点做垂直于水平轴的直线,分别与目标基线L0和过程基线Li相交于两点(如图7),计算两点距离Δhi与同一方向整幅图像高度的比值,定义为条纹的重合度Ei,计算式为

(6)

像素点数目/个

挑选重合度最高的过程基线,并找到所对应彩色图样的序号,即可计算出全反镜的移动距离Δx。

2 实验系统搭建及实验过程

通过大量实验和不断改进,最终搭建包括迈克尔逊干涉仪、白光光源、He-Ne激光器、摄像头等主要部件的实验装置,如图8所示。

图8 实验装置图

3 实验及数据处理

实验以肥皂膜为典型液态薄膜进行实际测量和数据分析。

按照前述技术方案开展实验,以0.000 05 mm步长精调迈克尔逊干涉仪,得到插入肥皂薄膜前后干涉条纹图样如图9所示。

图9 插入薄膜前后选定条纹位置

借鉴文献[13-14]所述技术方案,搭建实验装置对所配置肥皂溶液的折射率进行了测试,结果为n=1.453 0。

实验所测得原始数据如表1与表2所示。

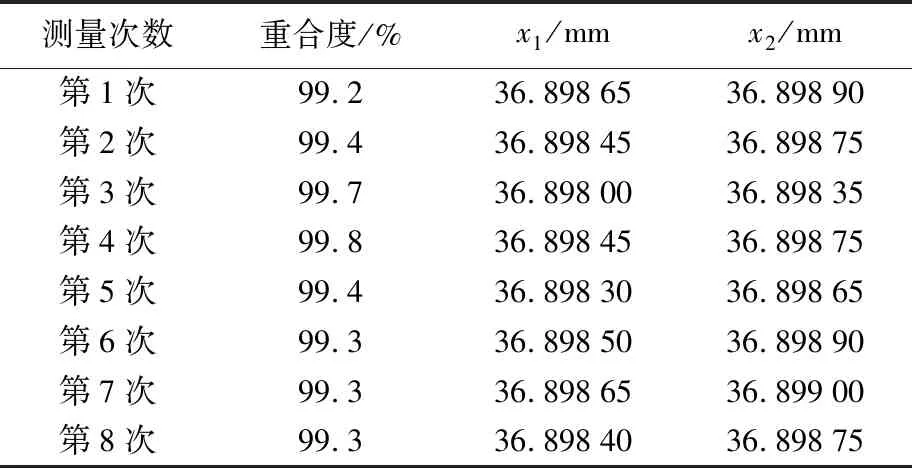
表1 图像处理法测量数据

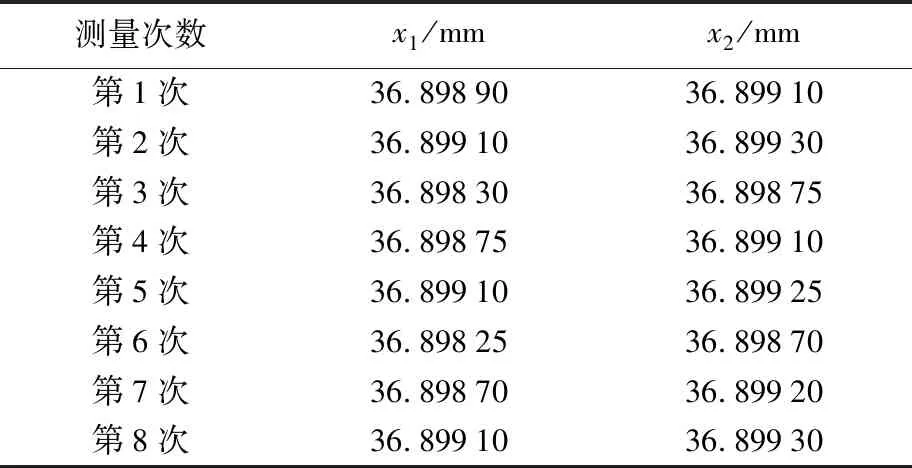
表2 目视估算法测量数据

因肥皂薄膜厚度与所用材料及配比有关,因此在进行数据处理时依据不确定度理论评价测量结果的可信度[15-19]。

综合考虑测量误差与仪器本身误差,引入A类不确定度与B类不确定度,计算得到采用图像处理法和目视估算法所得待测薄膜样品的厚度分别为:(0.73±0.08) μm和(0.69±0.23) μm,相对不确定度[20]分别为10.9%与33.3%,从数据可知,图像处理法所得到膜厚的相对不确定度更小,因此,图像处理法测量的准确度高于目测估算法。

4 结 论

本文以实验室常用的迈克尔逊干涉仪为核心仪器搭建了测试平台,在深入研究光学干涉原理的基础上,通过大量的实验总结出“激光+白光”的彩色干涉条纹调试方法,并引入图像处理技术,在python平台自主开发干涉图像分析算法,实现了液态薄膜厚度的高精度、低成本、高效测量。以肥皂薄膜为样例开展实验,数据表明图像处理技术与目视估测法相比在精确度和一致性方面有明显优势。