基于深度森林的磨矿粒度软测量模型的实现*

秦 楠 骆 俊 程小舟 刘自杰 孙 晨 张思涵徐瑞玲 陶 陶

（1.中钢集团马鞍山矿山研究总院股份有限公司；2.安徽工业大学计算机科学与技术学院；3.中钢矿院(马鞍山)智能应急科技有限公司）

在全球化的大背景下，矿产品的稳定供应对于国家经济的安全和持续发展至关重要［1-2］。选矿是非煤矿山重要的组成部分，稳定选矿生产，提高生产效率，降低能耗，提高选矿生产指标尤为重要。选矿工艺流程主要包括破碎、筛分、磨矿分级、选别、尾矿浓缩等，磨矿分级起着承上启下的作用。通过合理的磨矿分级，可以有效提高磨机的台时处理能力，使有用矿物与脉石充分解离，为后续的选别作业提供合适的条件。

磨矿分级一般采用磨机与水力旋流器闭路流程，通过对磨机运行状态的检测与控制、工艺参数的检测与控制、旋流器生产过程的控制，实现稳定溢流粒度、提高分级效率的目的。旋流器溢流粒度稳定在一定范围内，是衡量磨矿分级效果的关键指标。现阶段，溢流粒度的检测主要通过人工取样化验和仪表检测。人工取样存在滞后性，生产无法实时调节，影响产品质量。仪表检测投资成本高、易出现故障、维护量大，检测精度不能满足指标要求。为此，本文提出一种基于改进深度森林的机器学习方法，以实现溢流粒度分布的在线实时预测。

1 磨矿分级作业工艺流程

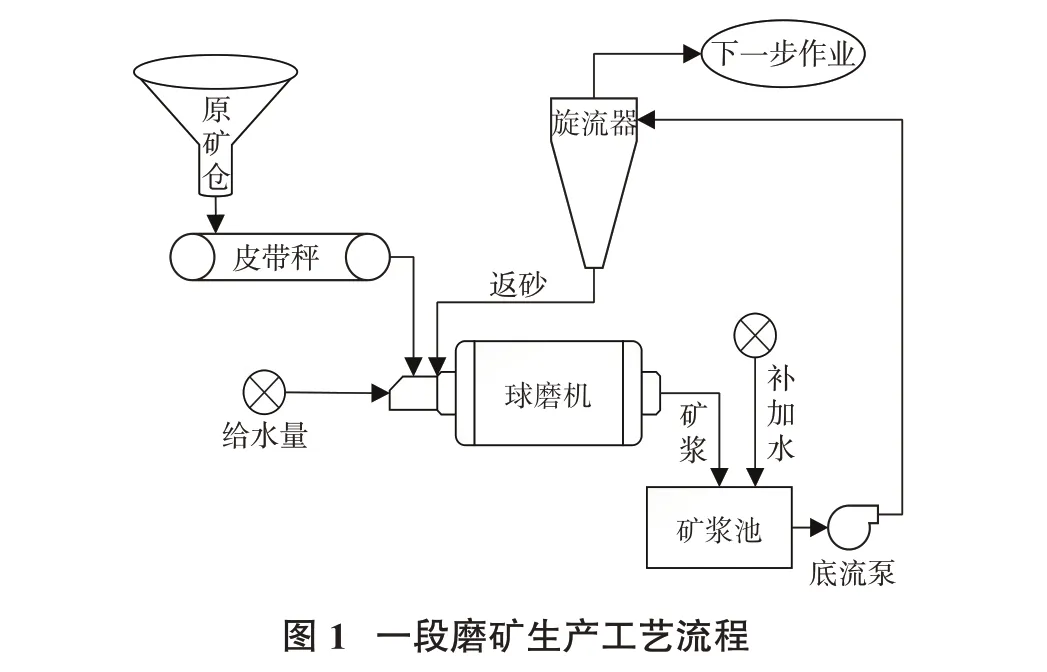
以某选矿厂一段磨矿分级环节为研究对象，预测一段磨矿流程中旋流器的溢流粒度分布，工艺流程见图1。

原矿仓矿石通过下料设备进入给矿皮带，经过给矿皮带进入球磨机，利用皮带秤计量矿石的矿量。球磨机中的磨矿浓度由矿量按比例加水间接控制，球磨机排出的矿浆经内部管道进入矿浆池，矿浆池加水调节矿浆浓度，经底流泵打入旋流器，旋流器溢流进入后续选别作业，旋流器返砂进入球磨机二次球磨［3］。设备包括给矿皮带、球磨机、矿浆池、底流泵、旋流器等生产设备，液位计、流量计、皮带秤、压力计、浓度计、粒度计等在线检测设备。工艺参数包括磨机给矿量、磨机给水量、磨机浓度、矿浆池液位、补加水流量、旋流器给矿压力、给矿流量、给矿浓度、溢流浓度、溢流粒度、返砂比。

磨矿过程是一个机理复杂、影响因素多、非线性、大滞后的时变系统，生产设备众多，难以建立所有控制参数的数学模型，且矿石硬度和粒度对球磨机运行特性有较大影响，各环节相互作用，相互影响。因此，磨矿分级作业控制要求在保证产品质量的前提下，最大限度地提高球磨机的处理能力，降低能耗。

2 基于改进深度森林的磨矿粒度软测量模型的建立

深度森林模型是由南京大学周志华课题组提出的一种基于随机森林［4］的深度学习模型。深度森林算法所需参数较少、鲁棒性强、可自动调整复杂度，对于高维、大量、复杂的数据处理问题，可以提高模型的预测能力和泛化能力，从而有效地提高数据处理效率和质量。本试验基于深度森林算法建立了回归模型，预测溢流粒度分布，深度森林模型建立流程见图2。

本文选取某选矿厂的实际生产数据，时间长度为120 d，数据采样率为1 min1 次，总样本数量为172 800，单样本包含19 个特征属性。试验模型基于深度森林模型进行改进，添加了特征提取层以提升模型输入质量和训练速度，改进多粒度扫描过程以增强深度森林的特征学习能力，模型整体运行流程如下。

（1）数据预处理。使用Python 读取数据集D，对数据集中的缺失值使用线性拟合法进行填补，针对异常值使用均值滤波进行值替换，之后将数据集D按7∶3的比例划分为训练集D1和测试集T1，D1∈Rl×m，其中l表示训练集D1的样本数大小，m表示特征变量的个数。

（2）输入特征提取。对训练集D1中的单个样本，随机打乱n次并保存为一个二维矩阵，所有样本对应产生二维矩阵的集合Matrix。使用二维矩阵集合Matrix训练单个一维卷积神经网络Conv 和其连接的线性层Linear。其中Conv 的输入通道数即为打乱次数n次，输出通道数设为1，调整卷积的核大小和步长使之输出向量大小为m/2，其连接的线性层Linear 的输出为1，即下一时刻的溢流粒度。当卷积神经网络Conv和线性层Linear训练完成后，仅使用预训练的卷积神经网络Conv 产生的中间向量，其包含的m/2 个特征作为改进深度森林模型的输入。

（3）设定训练参数。设定深度森林回归模型中的一些初始参数，如每个森林中决策树的数目n，滑动窗的大小di，对应窗口大小的步长stepi和滑动次数上限limiti等。与传统过程不同，对多粒度窗口滑动过程进行人为限制，减少了深度森林生成的时空复杂度，避免了内存溢出问题，具体设置见表1。

?

（4）多粒度窗口滑动。使用大小为di的滑动窗，分别对训练集D1进行拆分，生成不同大小的特征向量gvi。对滑动窗di提取出来的特征向量gvi分别用于训练随机森林模型和完全随机森林模型，生成2个不同的局部特征向量并连结，最终生成特征向量gi。

（5）模型生成。将上一阶段中生成的特征向量gi用于训练级联森林，gi经过级联森林的第ni级产生一个增广特征向量agni，将agni和最初的特征向量连结为第i个滑动窗第n级的特征向量gni。计算特征向量gni的训练误差，随着误差逐渐降低，将当前的特征向量作为下一层联合森林的输入，当误差连续3层不再降低，则终止训练过程，确定级联森林级数。

（6）产生预测结果。级联森林最后一层作为评估层，计算所有森林预测的平均值，即为最终深度森林回归预测的结果ŷ。

该模型对多粒度扫描的过程进行了改进。传统深度森林对多粒度扫描产生的子样本的全部结果进行拼接作为其输出，针对这部分输出，本研究利用不同的评价指标评估子样本的预测性能，选择性能最优的前85%子样本拼接，作为改进的输出结果（图3）。改进的多粒度扫描方法可有效提高模型的预测准确性，在增强深度森林的特征学习能力的同时，避免性能较差的子样本对模型结果造成负面影响［5］。

深度森林模型的复杂度可根据检验集的情况自动调整，通过设置较少的超参数，模型便可在不同规模数据集上具有优异的预测性能和较高的准确性。选择不同的森林模型（本试验采用随机森林模型和完全随机森林模型各2个），增加基模型的多样性，提高集成学习效果。试验中利用训练集D1，分别对每个森林中决策树数量（n_trees）和深度森林模型中决策树的最大深度（max_depth）2个参数调优，具体参数取值见表2。不同决策树的最大深度下，均方误差MSE 随决策树数量变化的曲线见图4。

?

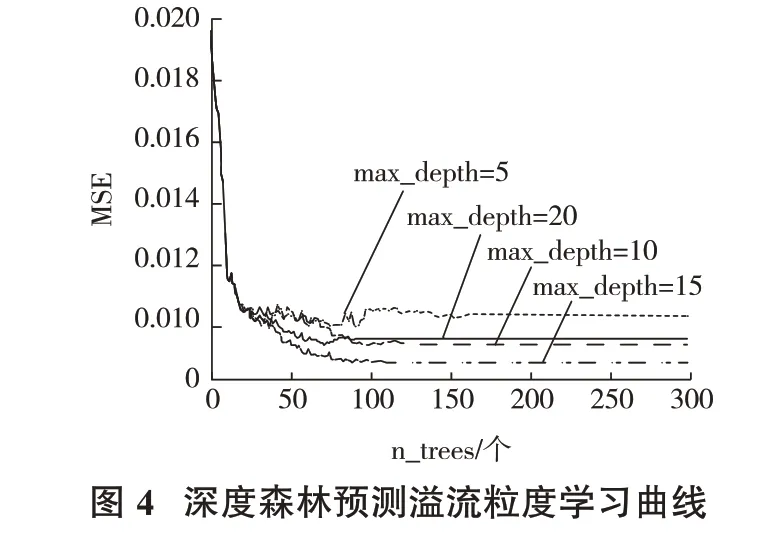
由图4 可见，n_trees 在0～50 时，MSE 下降速度较快；n_trees 在50～100 时，下降变缓；n_trees 大于150 时，MSE 趋 于 平 缓；综 上，取n_trees 为150，max_depth为15时，MSE 结果较好。

改进深度森林回归模型预测溢流粒度的初始参数设置见表3，训练好的改进深度森林模型用来预测测试集数据。

?

在改进深度森林算法预测溢流粒度的回归模型中，max_depth 取15，n_trees 取150，作为改进深度森林模型的初始参数。改进深度森林模型对溢流粒度分布预测的试验结果显示，训练集均方误差为0.009 71，决定系数为0.940 51，测试集均方误差为0.010 53，决定系数为0.929 64。测试集取前100条数据，其溢流粒度分布的真实值和预测值的比较结果见图5。

3 试验结果分析

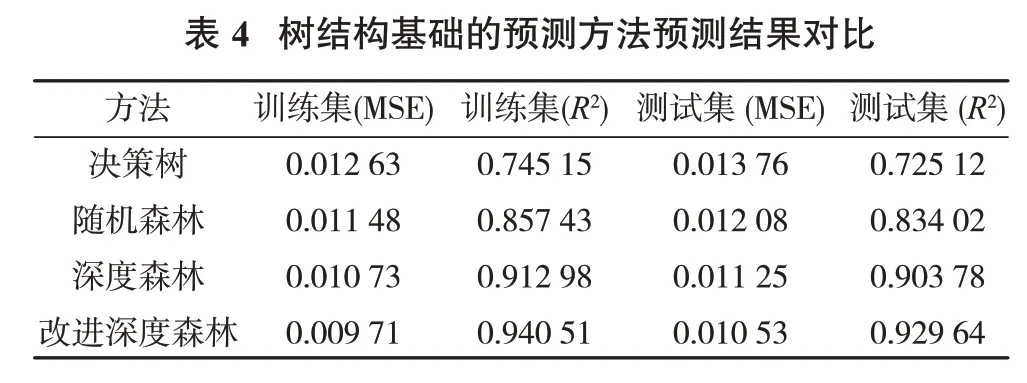
统一试验条件下，利用决策树、随机森林、深度森林、改进深度森林这4种以树结构为基础的预测模型训练样本数据，并对测试集T1进行测试，预测结果见表4，预测溢流粒度绝对误差对比见图6。

?

使用改进深度森林算法，在深度森林的基础上，对输入特征进行精练，改进多粒度扫描过程，增加基模型的多样性，提高集成学习效果。最终改进深度森林的训练集的R2达0.940 51，MSE 为0.009 71，测试集的R2为0.929 64，MSE 为0.010 53，改进深度森林模型比决策树、随机森林和深度森林模型训练集损失分别降低了23.1%、15.4%和9.51%，测试集损失分别降低了23.5%、12.8%和6.4%，预测性能较好，准确性较高。

由图6 可见，统一试验条件，选择测试集前50 条数据，和决策树、随机森林及传统深度森林模型相比，改进深度森林模型预测溢流粒度的绝对误差总体较低，显示出改进深度森林算法预测溢流粒度分布情况准确性较高。

为验证改进模型对比其他方法的效果，试验选取了传统的数学模型和主流的序列预测模型，在相同的试验条件下对比改进深度森林算法与ARIMA算法、指数平滑算法、LSTM 模型、RNN模型、Transformer模型的预测效果。预测结果见表5，预测溢流粒度绝对误差对比见图7。

?

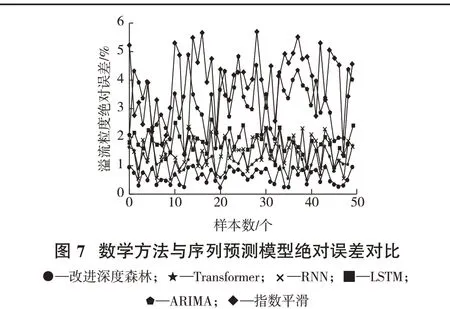
由表5和图7可知，对比数学预测方法ARIMA和指数平滑，改进深度森林模型具有较好的预测性能，而对比主流的序列预测模型，改进深度森林模型也具有一定的领先优势。总的来说，改进深度森林算法对本身的结构过程进行了一定的优化，在多领域算法试验对比上验证了模型在溢流粒度预测方面的有效性。

4 结 语

针对矿业生产中溢流粒度的预测问题，将特征提取层引入深度森林模型中，对深度森林的多粒度窗口滑动过程进行调整，改进了多粒度扫描的过程。通过选取某选矿厂的真实生产数据进行验证，将改进模型与多领域的传统算法进行对比，通过试验验证了所提出的改进深度森林模型在溢流粒度预测方面的优异性。