自动化立体仓库堆垛机路径优化方法研究

杨增钢，闫 明，雷 蕾 YANG Zenggang, YAN Ming, LEI Lei

（沈阳工业大学 机械工程学院，辽宁 沈阳 110870）

目前在使用遗传算法解决路径优化问题方面，主要分为两个维度。一是横向维度：多算法结合；二是纵向维度：将遗传算法升级。本文从横向、纵向两个维度同时对现有算法进行改进。在纵向维度，将现有自适应遗传算法中交叉、变异公式进行改进，形成IAGA 算法，以解决AGA 在进化早期出现“停滞”的问题。在横向维度，将IAGA 与SA 结合形成ASAGA 算法，以提高算法的精确度和收敛速度。

1 堆垛机调度建模

1.1 复合作业模式

复合作业方式工作过程为：从出入库站台O 点出发运行到第一个货位点进行入库操作，然后直接运行到第二个货位点，进行出货操作回到出入库站台，如此便完成了一组出入库作业。如图1 所示。

1.2 建立数学模型

考虑复合作业的实际工作情况，为使研究更方便，提出假设：

（1） 忽略堆垛机起速、降速时间；

（2） 堆垛机运动分解成两个正交方向的运动；

（3） 堆垛机收到一组指令，其中入库与出库指令数量均为k。堆垛机一次出入库作业时间为：

其中：tOA为入库运行时间，tAB空载运行时间，tOB出库运行时间。

由图1 可知，任意一组出入库组合任务中，无论其处于哪一个顺序位置上，OA 与OB 的距离是固定的，即tOA、tOB固定，而tAB（即空载时间） 却会因为相邻的入库与出库货位点的不同选择而发生变化，所以选择合适的出入库顺序使空载运行时间最短才是问题的关键。

采用单向配对的方式进行出入库任务处理，设A= ｛A1,A2,…,Ak｝，B= ｛B1,B2,…,Bk｝两个有序序列，Ak表示第k 个入库货位，Bk表示第k 个出库货位，则复合作业运行路径为：O→A1→B1→O→A2→B2→O→…→Ak→Bk。作业简化成如下方式：入库货位点集合A 按照订单自然顺序排列，作为待配对位置点，对出库货位点进行排序，使得总运行时间最小。

设A 中第i 个入库货位点的坐标为（xi, yi），重新排序后的B 中的第i 个出库货位点坐标为）。数学模型为：

式中：Vx、Vy为堆垛机水平、竖直方向运行速度，L 为货格的宽度。

2 自适应模拟退火遗传算法

2.1 自适应遗传算法设计步骤

（1） 编 码

采用顺序编码，整数的不同排列顺序即表示基因在染色体上的不同排列。

（2） 选择算子

本文采用轮盘赌法。基本思想：将个体适应度值占全部个体适应度总值的比例作为进入下一代的概率，概率公式为：

式中：f （xi）为个体i 的适应度值，为当代所有个体适应度值总和。

（3） 交叉、变异算子

a.交叉、变异方式：

采用两点交叉方式：随机选择两个交叉点的位置，两个交叉点之间的染色体片段即为交叉片段，两个父代交换交叉片段，其他位置上的基因按原来顺序且不重复原则排列在染色体上。

例如：

父代A （1,3,5,2,6,4 ）→子代A （3,5,2,1,6,4）

父代B （4,5,2,1,6,3 ）→子代B （4,3,5,2,1,6）

变异方式：随机选取两个基因位置进行交换。

例如： （1,3,5,2,6,4 ）→（1,6,5,2,3,4）

b.交叉、变异概率：

在Srinivasa[1]提出的自适应交叉、变异概率公式基础上做出改进，改进后公式如下：

由改进后的公式，避免了出现交叉、变异概率为0 的现象，进化早期保证当前最优个体能够继续进化，保证了全局收敛性。式中，fi表示要进行交叉运算的两个较大个体的适应度，K1、K2、K3、K4为常数，fmax为当代最大适应度值，favg为适应度平均值。

2.2 模拟退火算法

模拟退火算法具有跳突性，在于其Metropolis 准则：当个体A 为当前最优解时，算法不会将其直接输出为最终解，而是在其邻域随机扰动产生一新个体B。若B 适应度大于等于当前最大适应度fi，则直接接受该个体，并将B赋予A；若B 的适应度小于fi，则将根据Metropolis 准则：随机产生一个数Z∈（0,1 ），若Z≤exp （Δf/KT ）则接受B；反之，则不接受。其中，K为物理学常量，T 为当前温度。

2.3 自适应模拟退火遗传算法

为了彻底克服遗传算法过早收敛的问题，将改进后的自适应遗传算法（IAGA） 与SA 结合。结合方式如图2 所示：

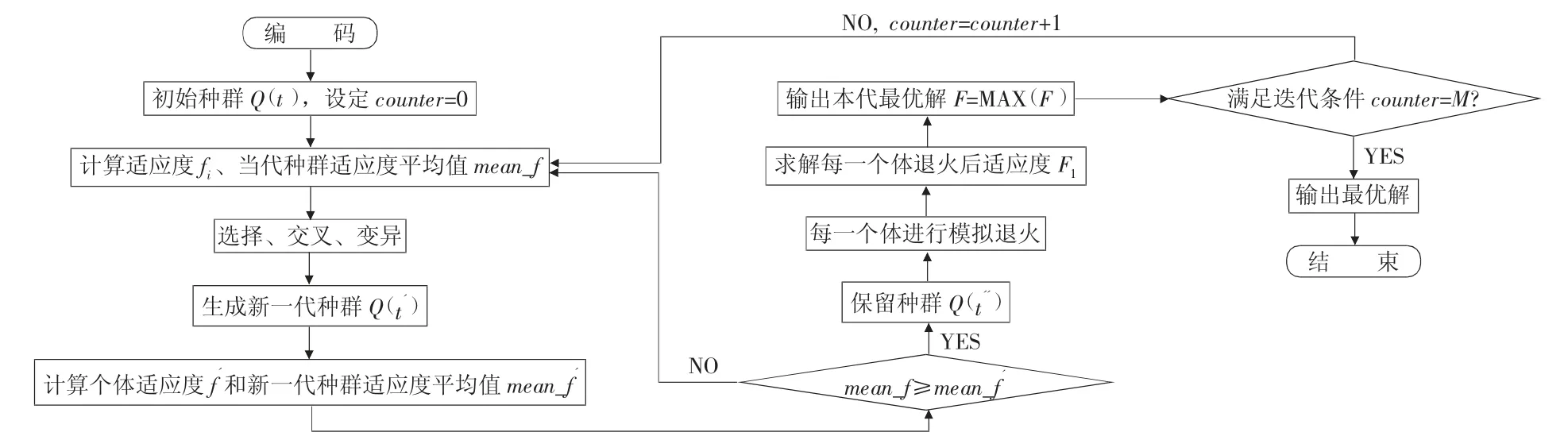
图2 ASAGA 流程图

结合方式：将遗传算法经交叉变异后，将新种群中每一个体均进行模拟退火操作，然后求解出每一个体的适应度Fi，并将这些个体组成新的组合F=max （F1,F2,…,Fn），当作本代一组最优解，作为下一代的初始种群。

3 仿真分析

3.1 参数设置

参数：货架：长100m，高30m，单元货格高度1m，宽度1m，共3 000 个货位；堆垛机：水平速度Vx=1.5m/s，竖直速度Vy=0.5m/s；随机生成40 条货单，30 条入库货单，30 条出库货单。

入库货单坐标： （2,1 8 ）（5,3 ）（20,16 ）（28,23 ）（35,12 ）（36 ,9 ）（42,28 ）（50,26 ）（58,24 ）（63,10 ）（64,15 ）（9,2 0 ）（12,20 ）（18,16）（29,13 ）（44 ,2 ）（59,17 ）（70,23 ）（72,15 ）（75 ,7 ）（79 ,1 ）（82 ,8 ）（84,30 ）（84 ,8 ）（89 ,2 ）（92,30 ）（98,21 ）（93 ,3 ）（99 ,8 ）（100,28 ）；

出库货单坐标： （3,5 ）（12,14 ）（17,21 ）（24,29 ）（29 ,7 ）（35,28 ）（43 ,6 ）（53,13 ）（60 ,2 ）（64,30 ）（66 ,2 ）（6,1 9 ）（14,25 ）（14,14）（26,30 ）（37,28 ）（38 ,2 ）（44,10 ）（47 ,9 ）（54,29 ）（65,18 ）（71,17 ）（76,13 ）（79,20 ）（80 ,5 ）（81,21 ）（88,10 ）（90 ,1 ）（93,30 ）（95 ,9 ）。

将出库货单依次编号1~30。种群规模N=100，初始温度T0=100，最终温度Tf=0.01，降温速率k=0.98，内部循环次数取50。

3.2 结果分析

使用Matlab 软件分别对各种算法运行20 次，分别取四种算法中最能代表结果平均值的一组数据，如图3 所示。

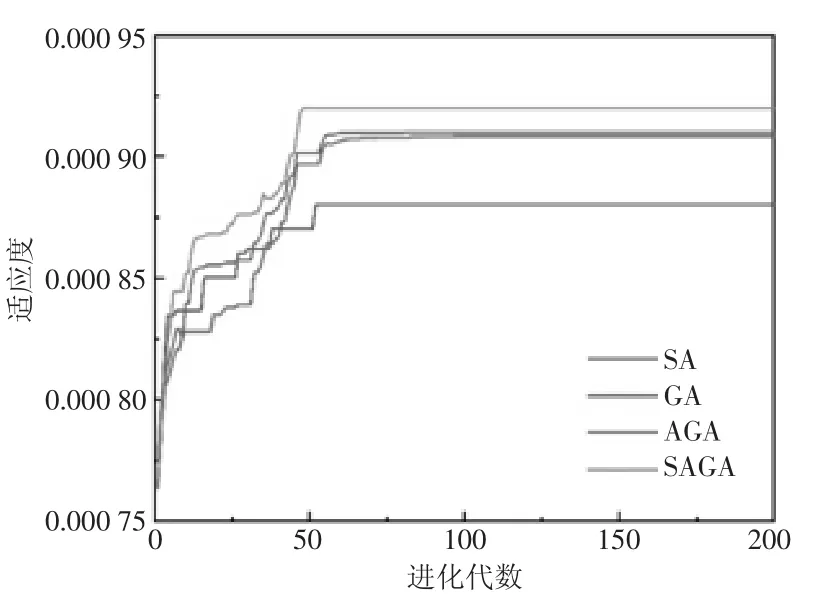
图3 四种算法最大适应度迭代曲线

由图3 看出，ASAGA 求解结果最接近理论最优值，适应度为0.000 92，即堆垛机最短作业时间为1 117s，货位出库顺序为12→1→2→4→18→7→16→6→20→19→8→3→13→14→5→17→21→24→22→23→9→25→15→27→11→10→26→28→30→29。

从纵向角度分析。IAGA 能够在算法进化初期避免出现陷入局部最优的现象，收敛速度有明显的提升，精确度也有一定幅度的提高。从横向角度分析。ASAGA 吸取了IAGA 全局搜索性强和SA 局部最优跳脱性的优点，在精确度和收敛速度上均有所提高。

4 结束语

本文研究自动化立体仓库堆垛机复合作业路径优化问题，建立数学模型，并使用SA、AGA、IAGA、ASAGA 四种算法求解，得到了最佳路径优化方案。并通过结果分析，证实了IAGA 能够解决AGA 在进化早期陷入局部最优的问题，ASAGA 能够在算法精确度、收敛速度两方面较SA、IAGA 均有一定提高，进而提高了仓库效率，降低了成本。