考虑尺寸误差与径向载荷的双螺母滚珠丝杠静刚度分析

陈光宇 翁直威 张 松

1.山东大学机械工程学院,济南,250061 2.高效洁净机械制造教育部重点实验室,济南,250061 3.山东普鲁特机床有限公司,滕州,277500

0 引言

滚珠丝杠作为一种精密传动功能部件,具有传动精度高、使用寿命长[1]的优点,广泛应用于高端加工中心、智能设备和其他工业领域[2]。实际应用中,因端部装配不当引起的径向偏心使得滚珠丝杠承受额外的径向载荷,直接影响着其机械性能,如轴向静刚度和位置精度[3-4]。同时,滚珠丝杠制造过程中产生的尺寸误差对其承载性能造成的影响也不容忽视。因此,准确地描述滚珠丝杠服役过程中相关尺寸误差和径向载荷对其承载性能影响的内在规律,建立准确的滚珠丝杠轴向变形位移和轴向静刚度计算模型,对滚珠丝杠的精密装配和高端应用具有重要的指导意义。

全滚珠的载荷分布显著影响滚珠丝杠的机械性能[5]。ZHOU等[6]、王恒等[7]、WEI等[8]分别描述了滚珠丝杠的预紧力与空载阻力扭矩之间的关系,提出了计算滚珠丝杠摩擦扭矩的理论模型,建立了滚珠丝杠的动力学模型,然而他们假设所有的滚珠都承受均等的载荷,存在一定的局限性。MEI等[9]分析了几何误差对单螺母滚珠丝杠滚珠载荷分布的影响,对相关研究产生了深远的影响。LIN等[10]提出了一个外部轴向载荷下考虑横向变形和几何误差的低阶静载荷分布模型,并进行了相关有限元分析计算。BERTOLASO等[11]采用应力场的光弹性法和位移场的标记跟踪方法测量了滚珠接触载荷和接触角的分布。ZHAO等[12]使用运动学方法分析了引入的变形系数与定义的几何误差系数之间的关系。

滚珠本身存在的尺寸误差[13]所造成的滚珠接触载荷分布不均影响着轴向静刚度,进而使得定位精度降低。程强等[14]、赵佳佳等[15]分别提出了考虑滚珠几何误差的滚珠载荷分布模型,通过计算传动过程中的行程变动量,可以较好地预测滚珠丝杠的位置精度。TAKAFUJI等[16]指出应考虑螺纹轴、螺母本身和螺纹的弹性变形来完善模型。KAMALZADEH等[17]分析了弹性接触变形对传动误差的影响,并提出补偿接触变形以提高滚珠丝杠的定位精度。XU等[18]指出,螺距与丝杠直径之比越大,载荷分布的均匀性就越差,滚珠丝杠的刚度性能也越低。

目前,关于双螺母滚珠丝杠轴向变形和静刚度的研究主要集中在仅承受外部轴向载荷的情况下,对同时承受轴向和径向复合载荷下轴向静刚度的研究相对较少。本文基于ZHEN等[19]和LIU等[20]进行的部分理论分析,主要建立了考虑尺寸误差和径向载荷的预紧双螺母滚珠丝杠轴向静刚度模型,揭示了尺寸误差、外部复合载荷、滚珠载荷分布和轴向静刚度的内在联系,并且在自主研制的滚珠丝杠加载试验台上进行了加载变形试验,验证了模型的正确性。最后,基于模型数值分析了外部径向载荷和尺寸误差对预紧双螺母滚珠丝杠轴向变形与静刚度的影响。

1 预紧双螺母滚珠丝杠的轴向静刚度模型

与单螺母滚珠丝杠相比,为了消除轴向间隙,提高轴向接触刚度,现代滚珠丝杠通常采用双螺母预紧结构。以广泛使用的双螺母垫片预紧式为例,首先需要准确计算出工作螺母与预紧螺母之间的轴向载荷分配。围绕工作螺母的载荷状态,通过描述全滚珠载荷分布计算出整个螺母的轴向变形位移,进一步可以获得轴向静刚度。在建立轴向静刚度模型时,本文同时考虑了尺寸误差和外部径向载荷的影响,并做出如下假设:①滚珠、丝杠滚道和螺母滚道之间的接触变形均在弹性范围内;②滚珠中心与丝杠滚道、螺母滚道的曲率中心在同一条线上;③滚珠与螺母滚道、丝杠滚道的接触角相同;④每个滚珠只承受丝杠、螺母接触区域的法向接触载荷,忽略相邻滚珠之间的相互作用。

1.1 预紧双螺母滚珠丝杠的复合受载状态

实际工程应用中,滚珠丝杠的安装不同于理想状态,往往存在着不同程度的径向偏心。这使得滚珠丝杠承受额外的径向载荷,螺母轴线相对于丝杠轴线产生偏移,丝杠和螺母之间全滚珠的载荷分布将不同于理想均匀状态而呈现出显著的不均匀性,进而影响轴向变形位移和静刚度。

在机床进给轴的传动结构中,螺母通过法兰固定在工作台下方,丝杠轴的两端安装在基体的轴承座内,其安装方式为一端固定一端支撑。当机床运行时,丝杠在伺服电机的驱动下通过滚珠将驱动力传递给螺母。螺母将通过连接法兰的螺栓承受作用在工作台上的复合载荷,主要包括外部轴向载荷Fa和径向载荷Fr,如图1所示。滚珠将在复合载荷的影响下产生相应变形,使得螺母相对于丝杠分别产生轴向变形位移δa和径向变形位移δr。

图1 预紧双螺母滚珠丝杠受载变形Fig.1 Load deformation of preloaded double-nut ball screw

如图2所示,在双螺母滚珠丝杠承受外部载荷之前,螺母A和螺母B将在预紧垫片的作用下发生一定量的初始变形,承受外部载荷后,工作螺母A的实际轴向载荷将相对于预紧力增大,而预紧螺母B的实际轴向载荷将减小。图2中,QAni、QBni(i=1,2,…,Z)分别为螺母A和螺母B中第i个滚珠与螺母滚道接触点处的法向载荷,Z为单个螺母中的滚珠数;βAi、βBi分别为螺母A和螺母B中第i个滚珠与螺母滚道接触点处的接触角。

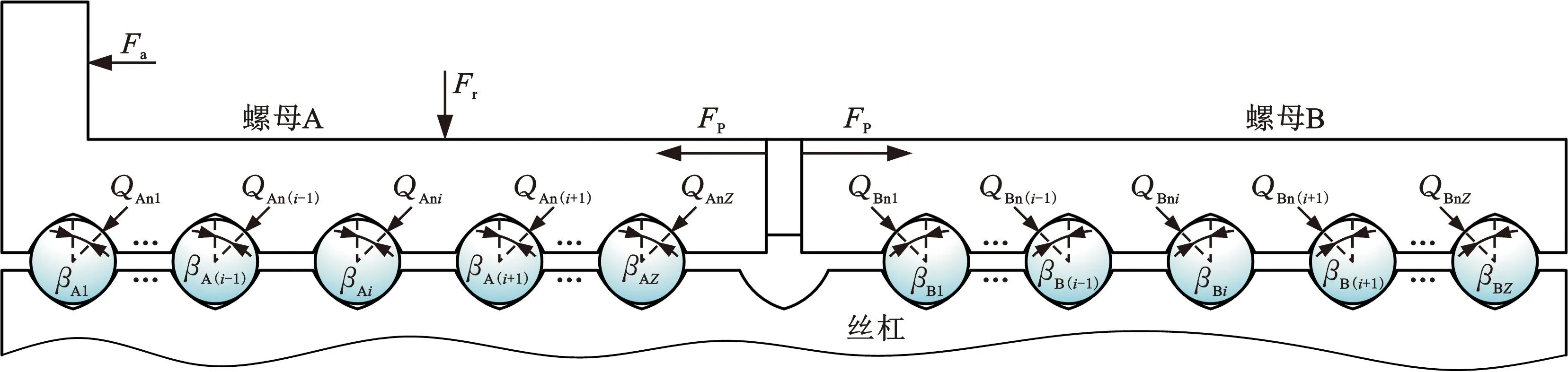
图2 预紧双螺母滚珠丝杠的多向受载Fig.2 Multi-directional load state of preloaded double-nut ball screw

在这种情况下,工作螺母A的实际载荷为FA,相对于预紧力FP的增量为F1,预紧螺母B的实际载荷为FB,相对于预紧的减小量为F2,可分别表示为

(1)

各参数之间的关系为

Fa=FA-FB=FP+F1-(FP-F2)=F1+F2

(2)

在外部载荷作用下,螺母A和螺母B的载荷状态发生变化,相应的轴向变形也会发生变化。工作螺母A将产生额外的轴向压缩变形,预紧螺母B将产生相应的恢复变形。当预紧垫圈被视为刚体时,它们的变形量应相等,可以表示为

δA-δP=δP-δB

(3)

式中,δP为仅预紧作用下螺母的轴向变形位移;δA、δB分别为预紧力和外部载荷共同作用下工作螺母A和预紧螺母B的轴向变形位移。

基于Hertz接触理论,δA、δB可以表示为

(4)

式中,K1为轴向接触变形系数。

联立式(3)、式(4),两螺母变形位移之间的关系可以表示为

(5)

因此,式(1)、式(2)、式(5)建立了求解两个螺母在预紧力和外载荷共同作用下各自轴向载荷分配的模型,其中F1值可以通过数值迭代法求解,进而得到FA和FB。

所有滚珠的法向接触载荷与工作螺母A的实际轴向载荷之间的关系可以表示为

(6)

式中,λ为滚珠丝杠的导程角。

图3展示了滚珠在滚道中的空间分布,其中rm为丝杠公称半径。每个滚珠的法向接触变形与螺母A相对于丝杠的径向接触位移之间的关系可以表示为

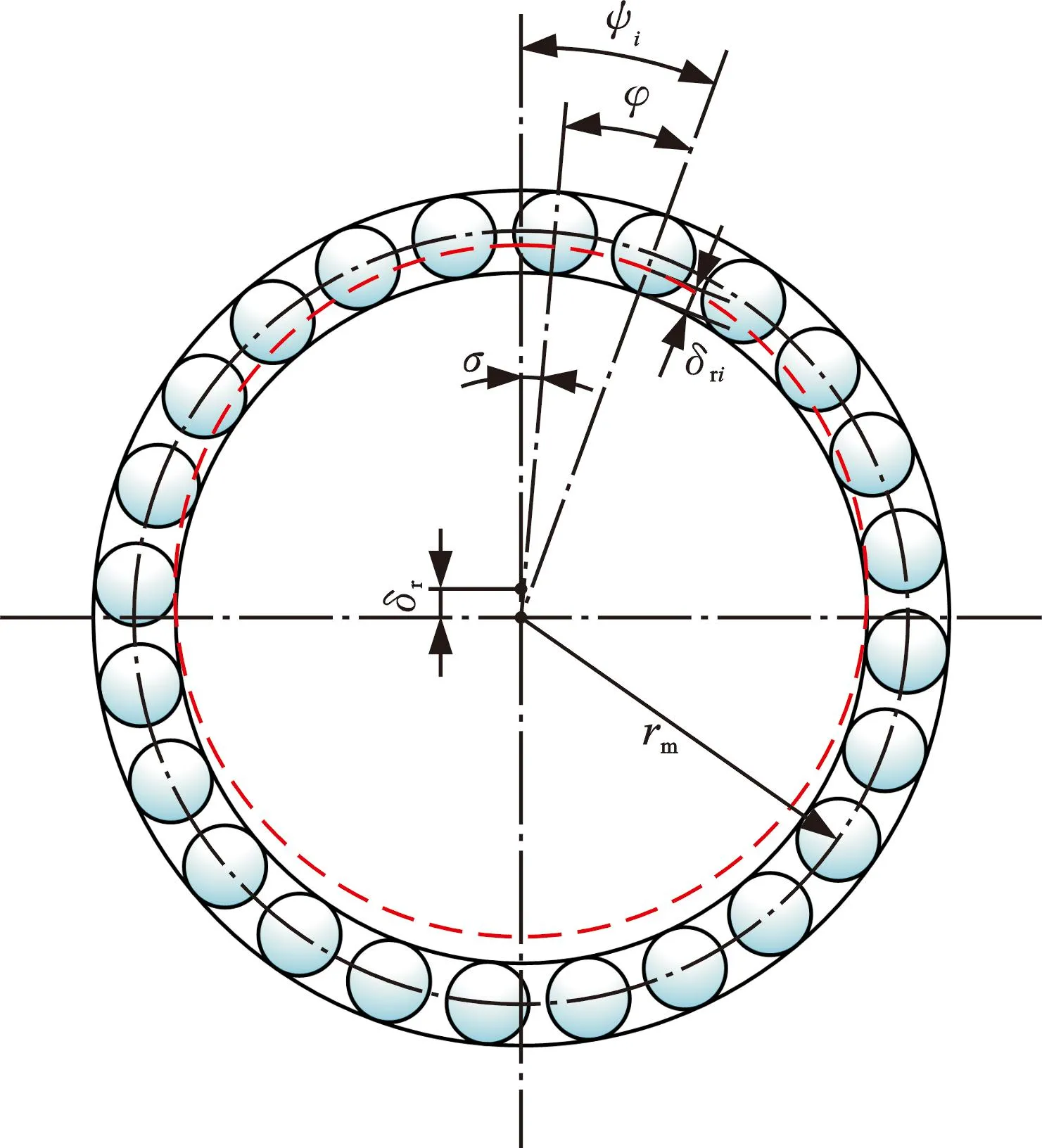
图3 滚珠在滚道中的空间分布Fig.3 Spatial distribution of balls in the raceway

δri=δrcosψi

(7)

式中,ψi为第i个滚珠在滚道中的位置角;σ为首个滚珠在滚道中的位置角;δr为丝杠轴线沿Fr方向产生的位移;δri为第i个滚珠沿径向的位移;φ为两个相邻滚珠中心的位置角;N为单个螺母中的滚珠列数。

根据径向载荷平衡条件,螺母A中所有滚珠的法向接触载荷与外部径向载荷Fr之间的关系可以表示为

(8)

1.2 理想情况下全滚珠载荷分布模型

根据上述分析,工作螺母A的实际载荷将随着外部轴向载荷的增大而增大。而外部径向载荷和尺寸误差的存在将使螺母中每个滚珠的法向载荷出现巨大差异,因此,有必要对螺母中所有滚珠的载荷分布状态进行分析和建模。

图4显示了螺母A中单个滚珠的初始接触状态。丝杠和螺母滚道的法向截面为双圆弧形状,其中β0为变形前的初始接触角,QAsi为螺母A中第i个滚珠与丝杠滚道接触点处的法向载荷。

图4 螺母A中的初始接触角Fig.4 Initial contact angle in nut A

图5 位置点的变形关系Fig.5 Displacement relation of position points

对于变形前的初始状态,丝杠滚道和螺母滚道的曲率中心之间的距离可以表示为

D=OnOs=rn+rs-db

(9)

式中,rs、rn分别为丝杠滚道法向截面半径和螺母滚道法向截面半径;db为滚珠的公称直径。

变形后,根据图5所示的空间关系,丝杠滚道中心在法向接触平面内的横向位移可表示为

(10)

其中,δAi为螺母A中第i个滚珠滚道法向截面内相关几何圆心的相对位移。同时,变形后丝杠和螺母滚道的曲率中心距离可以表示为

(11)

则螺母A中第i号滚珠与滚道之间的接触变形可以表示为

(12)

螺母A中第i个滚珠变形后滚珠滚道接触点处的接触角为

(13)

基于Hertz接触理论,接触变形与接触载荷之间的关系为

QAi=Kδ3/2

(14)

K=

式中,ks(e)、kn(e)分别为滚珠与丝杠、螺母之间接触点处的第一椭圆积分,e为中间参数;mas、man分别为滚珠与丝杠、螺母接触椭圆的短半轴系数;E′为等效弹性模量;∑ρs、∑ρn分别为滚珠与丝杠、螺母接触点的主曲率和;μs、μn分别为滚珠与丝杠、螺母接触侧的泊松比;Es、En分别为滚珠与丝杠、螺母接触侧的弹性模量。

结合上述各式,滚珠丝杠的全滚珠载荷平衡关系为

(15)

1.3 考虑尺寸误差的全滚珠载荷分布模型

滚珠丝杠的尺寸误差主要包括滚珠直径误差和丝杠导程误差。在滚珠丝杠传动过程中,滚珠的直径误差EDi直接影响滚珠的载荷分布,丝杠的导程误差EPi影响着螺母相对于丝杠的轴向变形,如图6所示。

图6 滚珠的尺寸误差Fig.6 Dimensional error of the balls

考虑到滚珠丝杠尺寸误差的影响,滚珠与滚道之间的接触变形修正为

(16)

滚珠与滚道之间的接触角修正为

(17)

存在误差时,滚珠丝杠的全滚珠载荷平衡关系修正为

(18)

1.4 预紧双螺母滚珠丝杠的轴向静刚度

尺寸误差和外部径向载荷的存在,使得不同空间位置的滚珠所承受的法向载荷显著不同。在承受外部载荷后,滚珠与滚道表面之间的法向弹性变形位移将导致螺母在轴向上相对于丝杠产生轴向变形。将预紧垫片视为一个理想刚体时,双螺母整体的轴向变形δx实际上是螺母在承受外部载荷后的轴向变形δa|Fa,Fr与螺母在初始预紧状态下的变形δa|FP之间的差值,可以表示为

δx=δa|Fa,Fr-δa|FP

(19)

式(18)和式(19)构成了求解复合载荷下双螺母滚珠丝杠副轴向变形位移的理论模型。对于滚珠丝杠,其静刚度可描述抵抗轴向变形的能力,当预紧双螺母滚珠丝杠承受外部复合载荷时,其轴向静刚度Ka实际为发生单位轴向变形位移所需要的外部轴向载荷的大小,可以表示为

(20)

因此,式(5)、式(18)、式(19)和式(20)构成了求解复合载荷下预紧双螺母滚珠丝杠轴向静刚度的理论模型。模型中包含了多个非线性方程,需要特定的迭代方法进行求解,并且针对多组外部复合载荷进行求解计算时需要单独迭代,从而可以获得多组轴向变形位移和静刚度。

2 模型求解和试验验证

2.1 轴向静刚度的求解计算

以R40-8T5-FDDC型预紧双螺母滚珠丝杠为例进行求解计算,每个工作螺母中有68个滚珠,其中60个滚珠在滚道中承受载荷,8个滚珠在反向器中不承受载荷,其具体参数如表1所示。

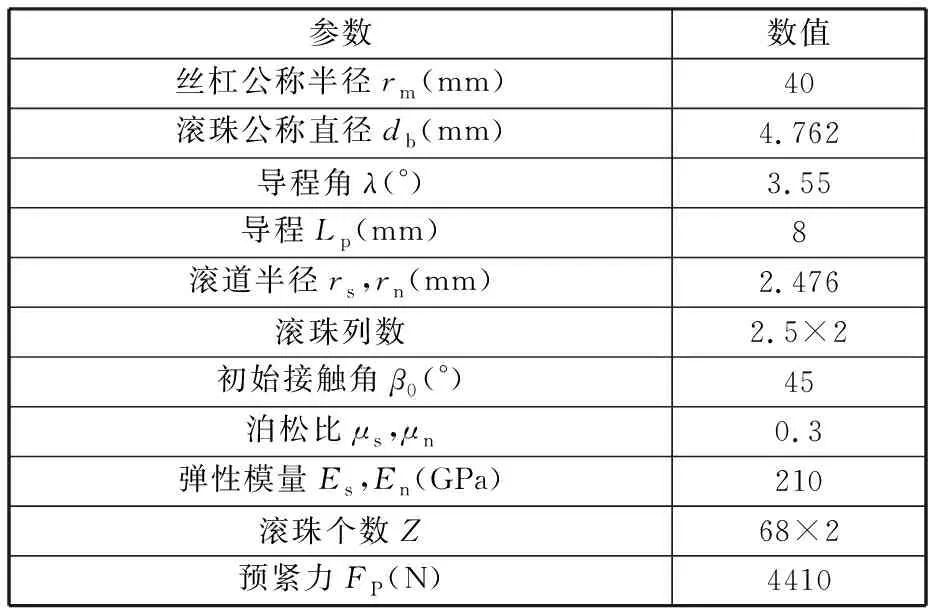
表1 R40-8T5-FDDC型滚珠丝杠的主要参数Tab.1 Main parameters of R40-8T5-FDDC ball screw

对于垫片式预紧结构,工作螺母A和预紧螺母B将由于外部载荷而同步轴向平移,因此它们的轴向变形位移应相同。随着外部轴向载荷增大,工作螺母A的实际载荷会增大,而预紧螺母B的实际载荷会相应减小,如图7所示。当外部轴向载荷增大到一定程度时,预紧螺母B的实际载荷减小到0,此时的外部轴向载荷称为临界轴向载荷Fl。此时,预紧螺母B中的滚珠与滚道脱离接触,仅工作螺母A承受载荷,相当于单螺母受载状态。且临界轴向载荷Fl与预紧力FP的大小有关。

图7 螺母实际受载随外部轴向载荷变化Fig.7 Actual axial load of the nuts varies with the external axial load

在具体的计算过程中,通过螺母载荷分配计算,将工作螺母A的实际载荷及其轴向变形位移作为整个螺母组合的轴向变形位移从而简化计算,并使用Newton-Raphson迭代法计算出整体轴向静刚度,具体求解流程如图8所示,其中eRR为载荷收敛判据值,Δδa、Δδr分别为δa、δr的增量。

图8 轴向静刚度求解流程Fig.8 Flow chart of solving axial static stiffness

2.2 试验验证

为了验证考虑尺寸误差和径向载荷的双螺母滚珠丝杠轴向静刚度模型,本文使用山东大学自主开发的滚珠丝杠复合加载试验台开展验证试验。试验台的主要结构组成如图9所示,包括滚珠丝杠、直线导轨、工作台、轴向电动缸、伺服电机、轴承、支撑导轨、龙门架、压力传感器、水平液压缸、垂直液压缸和光栅尺。通过测量双螺母滚珠丝杠在预定载荷下的轴向变形位移,进而获得其轴向静刚度,最后对试验结果和理论结果进行了比较和分析。

图9 滚珠丝杠加载试验台结构组成Fig.9 Structure of the ball screw loading test bench

本试验通过限制丝杠旋转并借助工作台向螺母同时施加轴向和径向载荷来达到载荷施加要求,过程中使用激光干涉仪(XL-80,Renishaw,英国)测量滚珠丝杠的轴向变形位移,进而通过换算获得轴向静刚度,试验的现场设置如图10所示。

图10 滚珠丝杠轴向变形试验现场Fig.10 Ball screw axial deformation test site

文献[21]指出,对于双螺母滚珠丝杠,螺母安装方式对轴向静刚度存在一定的影响,主要呈现在工作螺母的受载状态。为在最大程度上降低滚珠丝杠的安装方式对承载性能的影响,试验中滚珠丝杠的安装遵循螺母法兰靠近固定端的原则。在安装过程中,严格遵循装配工艺要求,多次使用激光校正安装,使丝杠两端轴承座和螺母座成三点一线,从而保证丝杠轴线和配套的导轨轴线平行,尽可能地减小安装误差对于测量数据准确性的影响。

试验台加载机构可同时向工作台施加外部轴向载荷和径向载荷。外部径向载荷施加0,2,4,6 kN四组水平。保持每组径向载荷不变时,外部轴向载荷从0缓慢增大到40%Ca(Ca为额定动载荷),即18 kN。激光干涉仪的当前位移测量数据每500 N记录一次。试验重复三次,取每个数据采集点的平均值作为最终测得的轴向变形位移。

对于测试中使用的R40-8T5-FDDC滚珠丝杠,根据工厂设置参数表和国家标准GB/T 17587.3-2017,丝杠精度等级为P3,滚珠精度为G16,具体参数见表1。根据文献[13]的相关研究,滚珠丝杠制造过程中产生的尺寸误差服从正态分布,由相应精度公差值和拉依达准则(3σ准则),将滚珠直径误差(μm)设置为N(0,(0.8/6)2),将滚道导程误差(μm)设置为N(0,(4/6)2)。以外部轴向载荷为X轴、测量的轴向变形位移为Y轴,绘制了不同外部径向载荷条件下测量数据的散点图。同时基于MATLAB软件,采用Newton-Raphson迭代法计算了预紧双螺母滚珠丝杠在不同径向和轴向载荷下的轴向变形位移,数值计算结果与试验结果的对比如图11所示。根据式(20)将试验变形位移换算为轴向静刚度值并与理论值进行对比,如图12所示。

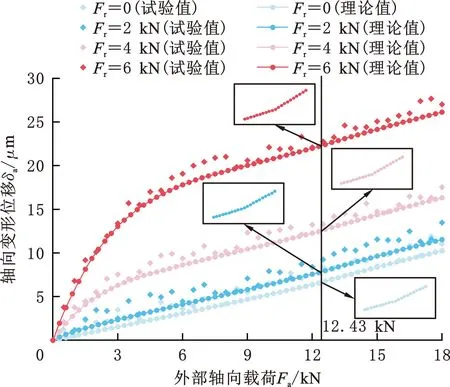
图11 轴向变形试验结果与理论结果对比Fig.11 Comparison of experimental results and theoretical results of axial deformation

图12 轴向静刚度试验结果与理论结果对比Fig.12 Comparison of experimental results and theoretical results of axial static stiffness

从试验结果对比中可以看出,轴向变形位移与轴向静刚度的试验值与理论值吻合良好。四个外部径向载荷水平下的平均相对偏差分别约为14.3%、13.8%、12.1%和9%,表明模型具有较高的计算精度。当外部轴向载荷达到12.43 kN时,轴向变形位移的曲线斜率增大,轴向静刚度呈现一次急剧下降的趋势。这是因为12.43 kN是预紧力FP为4.41 kN时双螺母滚珠丝杠的理论临界轴向载荷Fl。当外部轴向载荷大于12.43 kN时,预紧螺母B中滚珠与滚道脱离接触并失去预紧效果,此时只有工作螺母A承受轴向载荷,相当于单螺母受载状态。

根据1.1节中建立的螺母载荷分配模型,当预紧力FP=4.41 kN时,轴向临界载荷Fl为12.43 kN,对应的临界轴向变形位移为δl。图11中,当外部轴向载荷Fa为12.43 kN,外部径向载荷Fr为2,4,6 kN时,轴向变形位移δa均大于Fr=0时的位移值,也就是说Fr分别为2,4,6 kN时双螺母滚珠丝杠的轴向临界载荷Fl实际上会略小于12.43 kN。出现这一现象的原因是在螺母载荷分配计算过程中对径向载荷进行了简化处理,忽略了它造成的影响。

值得注意的是,图11中显示轴向变形位移的试验测量值通常高于理论值,轴向静刚度的试验值通常低于理论值。这是因为在建立模型时,主要考虑了滚珠与滚道间的接触变形,而忽略了实际工作台、轴承、丝杠、螺母等的变形和扭转刚度带来的影响。由于试验设备和条件的限制,无法准确测量试验台轴向传动系统各部件的准确变形,只能从整体变形位移的角度来验证模型的准确性,因此,本文建立的计算模型可以在一定程度上通过考虑外部径向载荷和尺寸误差来计算滚珠丝杠的载荷分布,进而获得预紧双螺母滚珠丝杠的轴向变形位移和轴向静刚度。

3 结果和讨论

3.1 外部径向载荷对轴向静刚度的影响

图13显示了预紧双螺母滚珠丝杠的轴向变形位移随外部轴径向载荷的变化。在保持外部径向载荷不变的情况下,当外部轴向载荷从0 变化到18 kN时,轴向变形位移相应按照不同的趋势增大。当外部径向载荷从0变化到6 kN时,滚珠丝杠的轴向变形位移急剧增大,并且变化得越来越快。当不承受外部径向载荷时,轴向变形位移随外部轴向载荷线性变化,这与LIU等[20]的模型计算相符。由图13可以看出,在外部轴向载荷较小的情况下,外部径向载荷对滚珠丝杠的轴向变形位移的影响更集中。当外部轴向载荷Fa<9 kN和外部径向载荷Fr>3 kN时,轴向变形位移变化非常剧烈,这是由于外部径向载荷使得部分滚珠与滚道脱离接触所致。

图13 轴向变形位移随外部载荷变化Fig.13 Variation of the axial deformation displacement with external loads

当外部轴向载荷Fa=5 kN、外部径向载荷Fr在1～5 kN之间变化时滚珠的载荷分布如图14所示。工作螺母A中的滚珠有2.5圈,相应的滚珠载荷分布呈现2.5个正弦周期。当外部径向载荷增大时,滚珠载荷分布的幅度相应地增大,滚珠的载荷分布峰值出现在1号、24号和49号滚珠上,它们恰好为工作螺母A的受力侧。随着外部径向载荷逐渐增大,滚珠上的最大法向接触载荷从202.38 N增大到510.23 N,最小法向接触载荷从125.35 N减小到0,所有滚珠的法向接触载荷极差从77.02 N增大到510.23 N。当外部径向载荷Fr>3 kN时,非承载滚珠开始出现,承载载荷的滚珠数量减少,每个滚珠将由于更大的法向接触载荷而发生更大的变形,因此滚珠丝杠将产生更大的轴向变形位移。

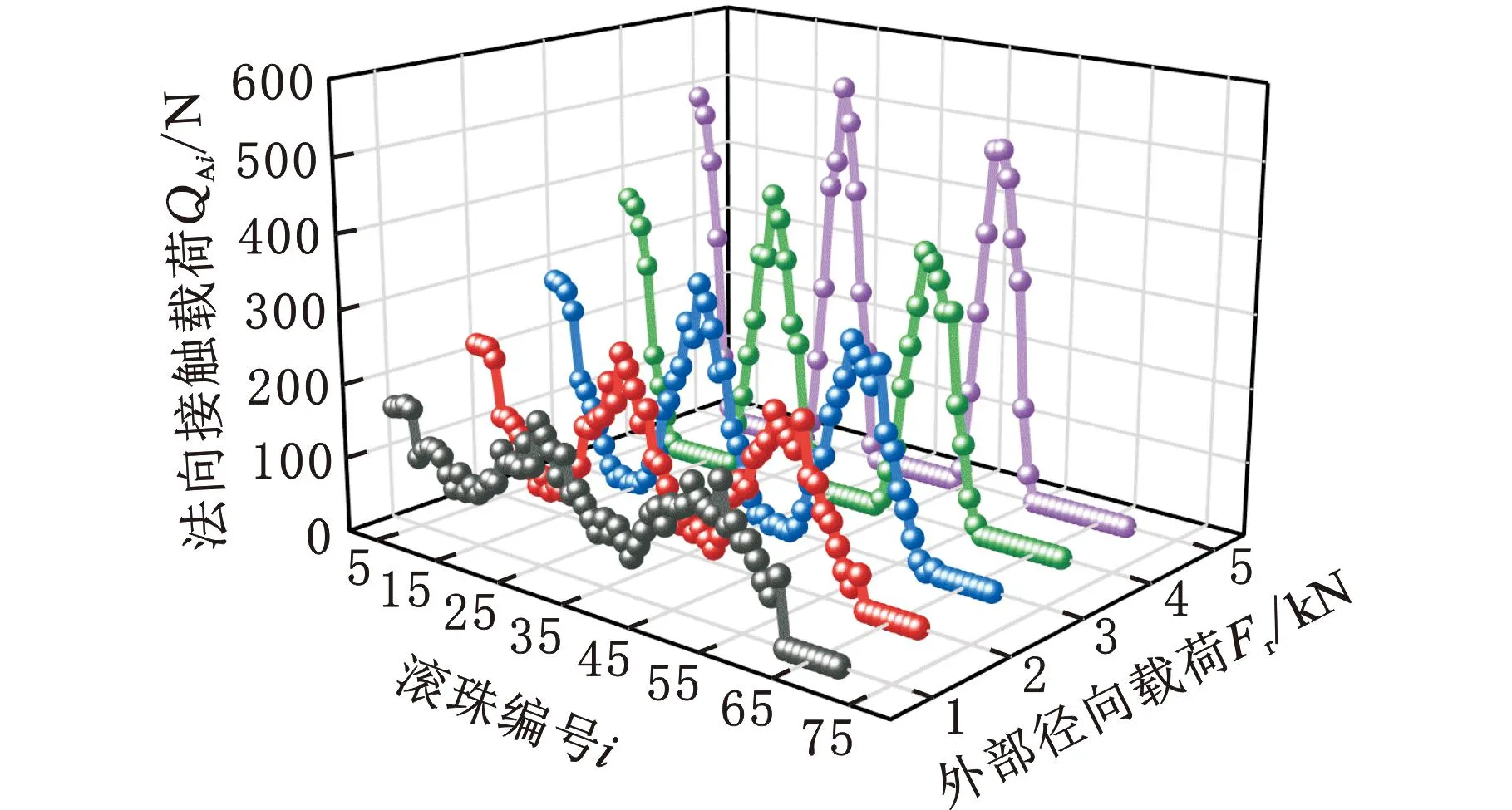
图14 Fa=5 kN时滚珠载荷分布随Fr的变化Fig.14 Variation of ball load distribution with Fr when Fa=5 kN

外部轴向载荷Fa=9 kN、外部径向载荷Fr在1～5 kN之间变化时滚珠的载荷分布如图15所示。与Fa=5 kN相比,Fa=9 kN时每个滚珠上的载荷分布相应增大,但保持相同的周期性变化。随着外部径向载荷的增大,滚珠的载荷分布幅度增大,但增大的速度减小。滚珠的最大法向接触载荷从287.65 N增大到591.87 N,最小法向载荷从153.57 N减小到78.43 N,所有滚珠的法向接触载荷极差从34.08 N增大到513.44 N。当外部径向载荷较大时,不受载滚珠的数量显著减少,所有滚珠载荷分布的差异性变化缓慢。当螺母承受同样水平的外部径向载荷时,较大的外部径向载荷会使得承载滚珠的数量更多,滚珠载荷的差异性也同时减小。

图16展示了预紧双螺母滚珠丝杠的轴向静刚度随外部轴向载荷和外部径向载荷的变化。在保持外部轴向载荷不变的情况下,轴向静刚度随着外部径向载荷的增大而相应减小,并且减小速度越来越快。当外部轴向载荷较小时,外部径向载荷的增大使得轴向静刚度显著减小。然而,对于不同水平下的外部径向载荷,随着外部轴向载荷的增大,轴向静刚度呈现不同的变化规律。当受到较小的外部径向载荷时,随着外部轴向载荷的增大,轴向静刚度先减小后增大。当受到较大的外部径向载荷时,随着外部轴向载荷的增大,轴向静刚度先增大后减小再增大。

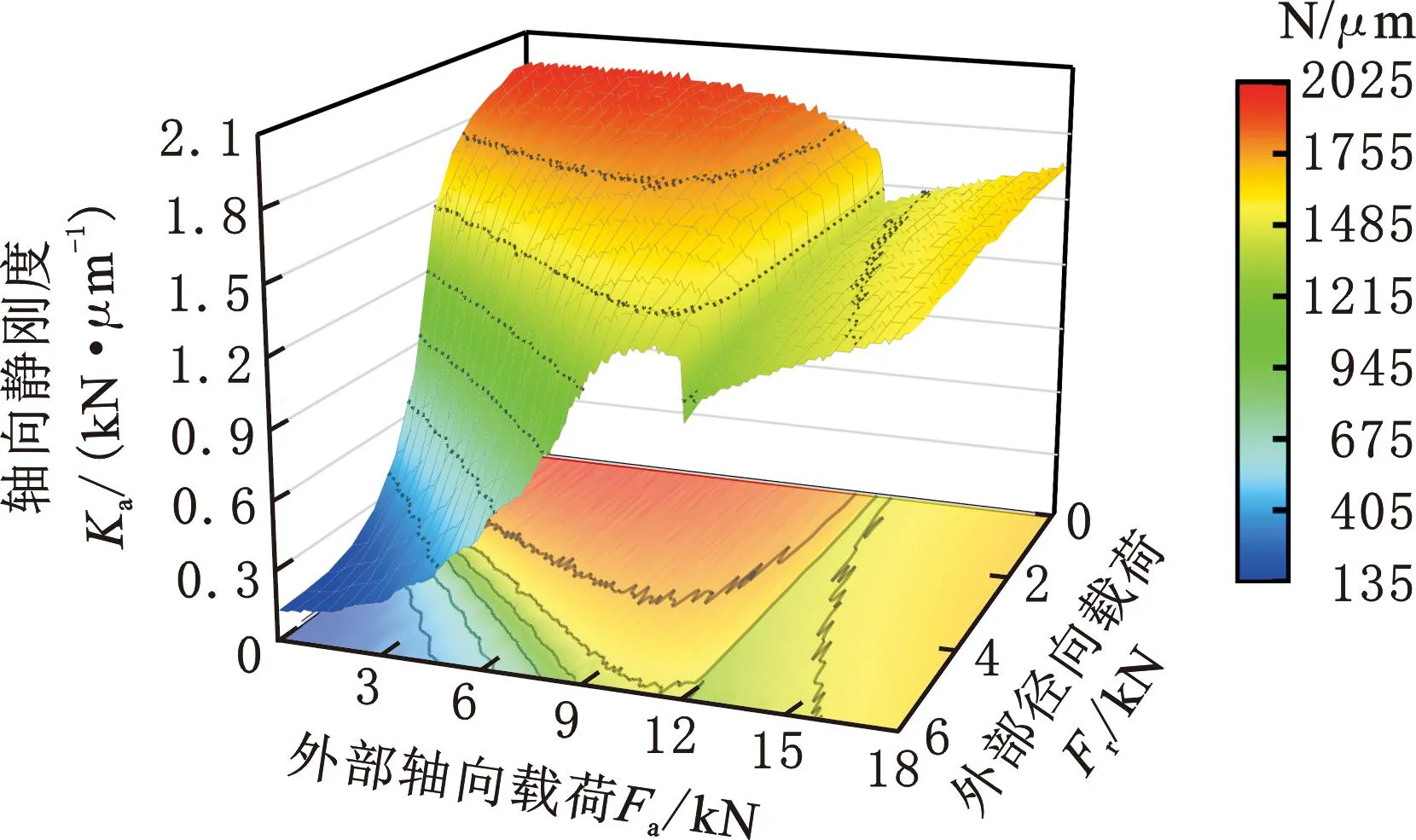
图16 轴向静刚度随外部加载的变化Fig.16 Variation of the axial static stiffness with external loads

当外部轴向载荷达到12.43 kN时,轴向静刚度同样呈现出一次骤降现象,这是因为12.43 kN是临界轴向载荷值,而预紧螺母B恰好处于卸载状态,此时相当于单螺母受载状态。当外部轴向载荷继续增大至超过双螺母滚珠丝杠的临界轴向载荷值时,轴向静刚度会随着外部轴向载荷的增大而增大。值得注意的是,通过较高的外部轴向载荷引起的足够大的弹性变形可以抵消由于外部径向载荷引起的滚珠受载不均而造成的双螺母滚珠丝杠的低刚度区,而这个抵消的范围随着径向载荷的增大而减小,这种现象也可以与前述的滚珠载荷分布变化得到印证。

3.2 尺寸误差复合外部径向载荷对轴向静刚度的影响

从模型的建立过程可以看出,滚珠的尺寸误差和滚珠丝杠滚道的导程误差对轴向变形位移和轴向静刚度具有相似的影响,因此,本文仅以滚珠尺寸误差为例,分析它对双螺母预紧滚珠丝杠轴向变形位移和轴向静刚度的影响。

滚珠的精度对滚珠丝杠的传动性能有重要影响。根据机械设计手册,具有不同滚珠精度的滚珠直径误差如表2所示。滚珠精度等级的数量越多,精度越低,滚珠直径误差越大。图17展示了根据MATLAB生成的每个滚珠精度等级服从正态分布的滚珠直径误差数据,用以分析滚珠丝杠的轴向变形位移和轴向静刚度的变化。

表2 滚珠精度及公差Tab.2 Ball precision and dimensional error

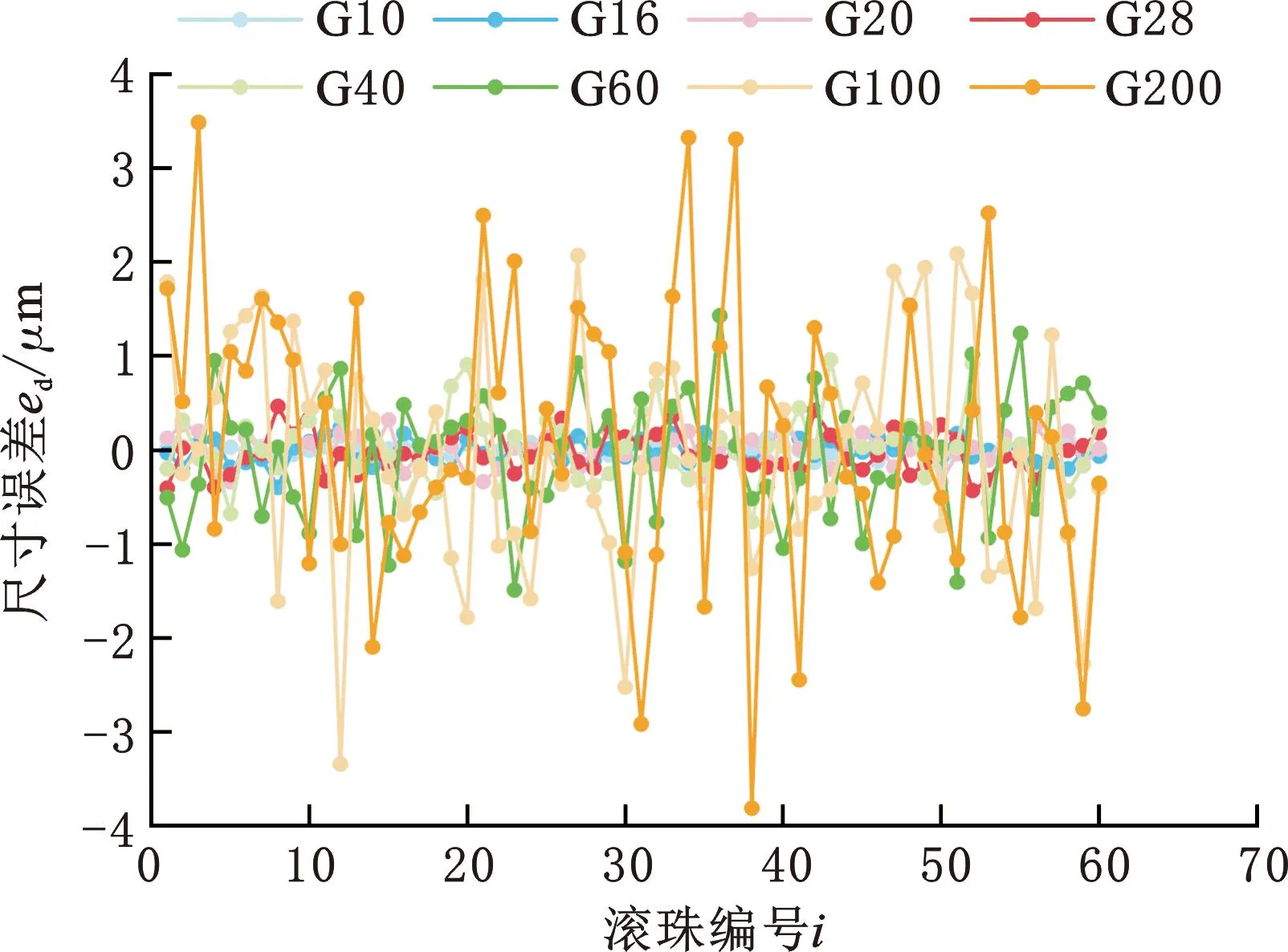
图17 不同滚珠精度产生的尺寸误差Fig.17 Ball dimensional errors due to different ball precision

图18显示了在外部轴向载荷Fa=5 kN和外部径向载荷Fr=1 kN条件下,工作螺母A的滚珠精度为G10～G60时的滚珠的载荷分布。随着滚珠精度等级的降低,滚珠的实际直径差异性明显,每个滚珠产生的法向接触变形变得不均匀。过大的滚珠尺寸会使滚珠承受过高的载荷,而过小的滚珠尺寸则会使滚珠承担较低的载荷,甚至会不受载,使滚珠的载荷分布发生很大变化。全滚珠的不均匀载荷分布会显著影响滚珠丝杠的轴向变形位移和轴向静刚度。

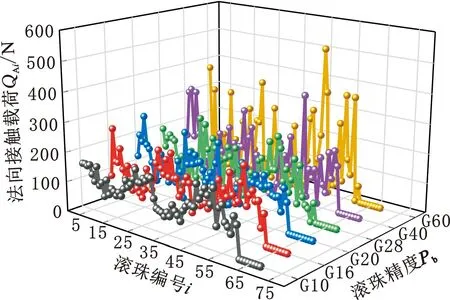
图18 Fa=5 kN、Fr=1 kN时滚珠载荷分布随滚珠精度的变化Fig.18 Variation of ball load distribution with ball precision when Fa=5 kN,Fr=1 kN

轴向变形位移随外部轴向载荷和滚珠精度等级的变化如图19所示。在相同的外部轴向载荷下,滚珠精度越低,滚珠丝杠的轴向变形位移越大。当滚珠精度为G10～G40时,轴向变形位移的差异并不明显,这是因为尽管滚珠之间存在尺寸差异,但滚珠之间的载荷分布波动性不够剧烈,且没有不受载滚珠,如图18所示。当滚珠精度继续降低到G60、G100和G200等级时,轴向变形位移显著增大。这是因为不同滚珠之间的尺寸差异过大,从而导致产生更多的不受载滚珠,因此轴向变形位移随着滚珠精度的降低而增大,并且变化得越来越快。

图19 轴向变形位移随滚珠精度的变化Fig.19 Variation of axial deformation displacement with ball precision

滚珠精度影响滚珠载荷分布引起的轴向变形位移的变化,同样影响着轴向静刚度。当保持外部径向载荷Fr=1 kN时,预紧双螺母滚珠丝杠的轴向静刚度随外部轴向载荷和滚珠精度的变化如图20所示。在相同的外部轴向载荷下,随着滚珠精度的降低,滚珠直径误差的增大导致轴向变形位移增大,滚珠丝杠的轴向静刚度相应降低。这种刚度的降低适用于整个轴向外部载荷范围。随着外部轴向载荷从0增大到3 kN,轴向静刚度略微增大。原因是外部轴向载荷抵消了外部径向载荷引起的低刚度效应。然而,由于滚珠精度的降低,这种抵消低刚度的效应是不够的。随着外部轴向载荷持续增大直到超过丝杠的临界轴向载荷,不同滚珠精度下的轴向静刚度同步降低,当外部轴向载荷达到临界外部轴向载荷时,轴向静刚度急剧减小而后继续增大,与前述情况一致。结合图18中不同滚珠精度下的滚珠载荷分布情况,较低的滚珠精度会带来较大的滚珠直径误差,且会减少实际承受载荷的滚珠数量,从而降低滚珠丝杠的轴向静刚度。

图20 轴向静刚度随滚珠精度的变化Fig.20 Variation of axial static stiffness with ball precision

4 结论

本文分析了预紧双螺母滚珠丝杠在轴向和径向复合载荷作用下的协同变形关系。基于受力平衡,得到滚珠载荷分布模型,进一步计算了滚珠丝杠在不同载荷条件下的轴向变形位移和轴向静刚度。数值模拟了外部径向载荷和滚珠尺寸误差对滚珠丝杠轴向静刚度的影响。结论如下:

(1)工作螺母和预紧螺母分配的实际轴向载荷与临界外部轴向载荷和预紧力有关。当超过临界外部轴向载荷时,它实际上变成了单螺母接触状态,滚珠丝杠的轴向变形位移增大得更快,轴向静刚度呈现出先急剧减小、然后缓慢增大的变化趋势。

(2)随着外部径向载荷的增大,滚珠的法向接触载荷不均匀性增大,进而出现不受载滚珠,导致滚珠丝杠的轴向变形位移增大,轴向静刚度减小。当外部轴向载荷较小而外部径向载荷较大时,将表现出明显的“低刚度区”,而这种现象可以随着轴向载荷的增大在一定程度上被抵消。

(3)滚珠尺寸误差的增大同样会使得不同滚珠之间的负载差异变得显著。随着滚珠精度的降低,滚珠丝杠在相同载荷下的轴向变形位移增大,轴向静刚度减小。与径向载荷带来的低刚度影响不同的是,外部轴向载荷的增大并不能消除因滚珠精度降低而产生的“低刚度区”。

本文详细分析了考虑尺寸误差时预紧双螺母滚珠丝杠在轴径向复合受载过程中的轴向变形位移和轴向静刚度变化,这有助于指导预紧双螺母滚珠丝杠在静止或低速工况下的承载能力评估和精度设计。