层理面强度对水力裂缝缝网演化影响研究*

韩伟歌 彭皓睿 崔振东 朱正国 刘 利 张康健

(①石家庄铁道大学,道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043,中国)(②河北省金属矿山安全高效开采技术创新中心,石家庄 050043,中国)(③中国科学院地质与地球物理研究所,中国科学院页岩气与地质工程重点实验室,北京 100029,中国)(④中国科学院地球科学研究院,北京 100029,中国)(⑤中国科学院大学,地球与行星科学学院,北京 100049,中国)(⑥中铁十八局集团有限公司,天津 300222,中国)

0 引 言

随着世界经济技术的不断发展,常规油气资源日渐枯竭,全球战略目光均已向非常规油气资源转移。而非常规油气储层渗透率低,想要实现经济有效开采,需要对储层进行压裂改造,产生连通压裂缝网,为致密油气增加渗流通道,提高储层渗透率。而致密沉积储层层理面较为发育,层理面可以为水力裂缝提供较好地导流通道,层理面也将直接决定水力压裂缝网的复杂程度(刘玉章等,2017)。因此,探明水力裂缝与层理面的交互机制对揭示复杂压裂缝网的成因机理至关重要。

众多学者开展了室内水力压裂试验,观察了层理面对水力裂缝扩展的影响过程(侯冰等,2014)。侯振坤等(2016)通过页岩真三轴水力压裂试验提出软弱结构面的存在是复杂缝网形成演化的基础。李晓等(2019)通过对不同层理角度的页岩试样进行压裂试验,揭示了层理面倾角对裂缝扩展路径、孔压曲线和起裂压力的影响规律。孙可明等(2016)根据三轴水力压裂试验结果,得到层理方向决定了水力裂缝扩展方向。Daneshy(1978)通过理论和试验结合的方法研究了层理界面对水力裂缝扩展的影响。李芷等(2015)采用真三轴水力压裂试验,分析了水力裂缝与层理面交汇机制,水力裂缝在与层理面接触后天然层理面开始拉张或剪切破裂。衡帅等(2015)采用真三轴水力压裂试验,分析了层理在页岩压裂缝网形成中的重要作用。赵子江等(2019)采用循环渐进升压的排量控制方式,分析了页岩层理面激活沟通过程。此外,学者也对层理面其他特性及断层尺度和微纳观尺度(Cui et al.,2018; 崔振东等,2018; 冯雪磊等,2021)下的裂缝扩展过程进行了研究,Guo et al.(2018)研究了层理面密度对水力裂缝扩展的影响,并以此建立了3种裂缝扩展模型。赵海军等(2016)利用数值模拟,分析了不同尺度下的天然结构面对水力裂缝扩展与演化的影响。同时,油气储层中的天然裂缝可为油气提供更多的运移通道(霍健等,2021)。Huang et al.(2017)通过真三轴水力压裂实验揭示了层理面附近水力压裂的基本传播规律,提出水力裂缝的3种穿透模式。而这3种穿透模式在水力裂缝与天然裂隙相互作用数值模拟研究中也被众多学者认可,普遍认为水力裂缝与天然裂缝相互作用模式主要为:穿透、截获和偏转(Zhang et al.,2017; Zhou et al.,2017; 郭静芸等,2018; Fu et al.,2019)。而这种模式主要受地应力差和水力裂缝与天然裂缝的夹角影响(李勇明等,2015),通常认为较低地应力差条件或者水力裂缝与天然裂缝呈较小夹角时,水力裂缝容易被天然裂缝捕获。此外,Zeng et al.(2016)综合考虑了裂缝间距和天然裂缝对水力裂缝的影响,探讨了复杂裂缝网络形成机理,得到裂缝间距和应力各向异性对裂缝形态有显著影响。Nagel et al.(2013)也根据水力裂缝产生的应力阴影现象,分析了新生水力裂缝对原位地应力场的影响及其与天然裂缝之间的相互影响,得到水力裂缝引起的应力场变化会显著影响天然裂缝的状态,同时天然裂缝也影响水力压裂的成功性。目前研究结果均表明层理面的存在对裂缝的扩展具有重要影响(赵金洲等,2014; 王燚钊等,2018),而层理角度则主要决定岩石的破裂模式(张桂民等,2012; 张树文等,2017),直接影响裂缝形态,决定压裂效果。当前的研究热点主要聚焦在层理面角度对水力裂缝缝网演化的影响,但是层理面参数不仅仅有层理面角度,对于不同地区致密储层的层理面强度性质(胶结程度)也不相同,而目前对于层理面胶结程度对水力裂缝缝网演化影响的研究还较少。而揭示层理面强度对水力裂缝扩展的影响可指导不同地域针对性地设置压裂方案,对优化压裂设计,提高油气开采率具有重要意义。

本文通过Python编程对有限元数值模型全局嵌入了0厚度Cohesive单元,建立了含软弱层理面的离散网络模型,基于该模型研究了层理面胶结程度对水力裂缝扩展的影响,并进一步结合Matlab程序对Abaqus有限元软件进行二次开发,实现了声发射(AE)数值模拟,结合AE数值结果精细化分析了水力裂缝的扩展过程,揭示了水力裂缝与层理面的交互模式,为缝网形成演化机理分析提供重要理论支撑。

1 数值计算原理

1.1 黏性单元本构方程

黏聚力模型(Cohesive zone model)首先由Dugdale(1960)和Barenblatt(1962)提出,该模型可较好地解决裂纹尖端奇异性问题,可实现多种工况的裂纹扩展研究(沈珉等,2018)。Cohesive单元采用基于牵引分离规律的线弹性本构模型,在损伤开始前,应力-应变满足线弹性关系,即:

(1)

式中:t代表应力;ε表示应变; 下标n表示法向; 下标s和t表示两个切向方向;K为单元刚度。

1.2 Cohesive模型流-固耦合原理

1.2.1 应力平衡方程

岩石作为多孔介质其变形的力学平衡方程可由虚功原理给出(Han et al.,2020):

(2)

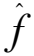
(3)

式中:ρw是液体的密度;g是重力加速度,软件里假设它在竖直方向上是恒定的。

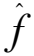
(4)

式中:f为不考虑流体重力的单位体积力。

1.2.2 裂缝面内流体流动模型

假设裂缝内的流体是连续且不可压缩的,则流体在裂缝扩展面单元中的流动可划分为切向流动和法向流动。

(1)流体切向流动方程:裂缝单元表面的切向流动可以用牛顿模型来模拟。在牛顿流体的情况下,体积流量可由以下表达式给出(Han et al.,2021):

Q=-ktp

(5)

式中:Q为排量;kt为切向渗透率;p为沿着破裂面的压力梯度。

切向渗透率可根据雷诺方程来定义:

(6)

式中:d为破裂单元裂缝面的张开位移;μ为压裂液黏度。

(2)流体法向流动方程:流体在破裂单元表面的法向流动可解释为流体流进模拟区域单元上的体积速率,对应于工程中的滤失现象。

流体在破裂单元上、下表面法向流计算公式(Han et al.,2021):

(7)

式中:qt、qb分别为流体进入破裂单元上下裂缝表面的体积流速;pt、pb对应上下表面孔隙压力;pi为破裂单元边上虚拟节点的流体压力;ct和cb分别对应上下表面滤失系数,其定义为单位面积、单位压差、单位时间的滤失体积。

1.3 裂缝扩展准则

1.3.1 损伤起始准则

本文采用最大主应力准则作为裂缝起裂准则:

(8)

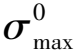
(9)

即cohesive单元在纯压缩状态下不会产生起始损伤。

1.3.2 损伤演化准则

损伤演化规律用于描述材料刚度退化的速率,定义损伤变量D来代表材料的总体损伤,D在损伤过程中从0演化到1。损伤变量对应力分量的影响可由下式给出:

(10)

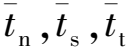
(11)

损伤变量D本文采用基于有效位移的线性软化形式来表示:

(12)

(13)

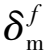
1.4 声发射数值模拟方法

声发射(AE)技术作为检测裂缝扩展的有效手段,可以连续、实时地监测裂纹的产生和发展,在岩石力学领域得到了广泛应用(He et al.,2010; 韩伟歌等,2017)。为了深入分析裂缝扩展过程,本文基于声发射方法的基本思想,采用Python编程语言对ABAQUS软件进行二次开发,结合MATLAB编程处理模拟数据在有限元里实现了声发射数值模拟技术,准确获取了AE定位图和AE特征参数。其基本思想如下(韩伟歌等,2019):

首先,提取所有损伤单元及开始损伤时间,统计不同时间下的损伤单元数,以此作为声发射事件数; 其次,获取损伤单元的节点坐标和耗散能,从而计算声发射事件点定位坐标及声发射能量; 最后,得到损伤单元参数MMIXDME以此判断裂缝破裂类型。MMIXDME参数定义如下:

(14)

式中:Gn、Gs、Gt分别表示3种破裂类型的断裂能。MMIXDME数值为0时表示纯拉破裂,为1时为纯剪破裂,两者之间则表示为拉剪混合破裂(韩伟歌等,2021)。

2 数值模型

岩石作为矿物集合体,由各种矿物颗粒组成,具有矿物非均质性,而页岩层理面又极为发育,需同时考虑页岩矿物非均质性及层理各项异性。

首先,建立尺寸为50m×50m的二维数值模型,在模型中心预制与最大主应力方向平行的初始裂缝作为射孔,射孔长度设为1m。同时,采用0厚度cohesive单元构建与最大主应力方向呈30°的层理面。为了实现裂缝扩展的随机性,通过二次开发对模型全局嵌入0厚度cohesive单元(图1),并分别对层理面处cohesive单元和实体单元间cohesive单元赋予不同材料属性,从而突出层理面软弱特征。

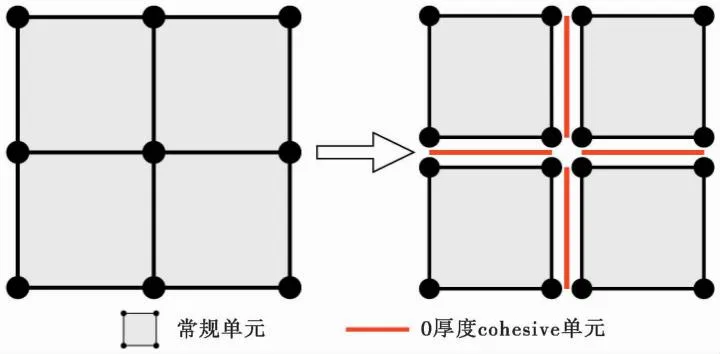
图1 嵌入cohesive单元示意图

此外,根据页岩XRD矿物成分分析结果,确定页岩所含矿物种类及占比(Cui et al.,2022)(表1),通过Python编程对ABAQUS模拟软件进行二次开发,以网格单元来表征矿物颗粒,通过将相同类型矿物单元建立成集合,并对不同集合进行赋值,实现不同矿物间的材料差异性,从而实现页岩矿物的非均质性。通过上述手段实现了矿物非均质性及层理面各向异性模型的建立(图2)。

表1 矿物成分及参数

图2 矿物非均质性模型

为了模拟不同层理面强度对水力裂缝扩展的影响,引入无因次层理面强度系数F:

(15)

式中:Tb为层理面cohesive单元的抗拉强度;Tr为实体单元间cohesive单元的抗拉强度。

通过将层理面处的cohesive单元设置为不同的强度参数,进行4种无因次层理面强度系数下的数值模拟试验,具体参数如表2所示。

表2 Cohesive单元参数

基于文献数据设置储层参数,水平最大主应力和最小主应力分别为13MPa和7MPa,最大主应力沿Y轴方向。渗透系数为10-7m·s-1、滤失系数为10-14m·(Pa·s)-1、压裂液黏度为0.001Pa·s、最大排量为0.01m2·s-1(Han et al.,2020)。模型网格单元数为68,806个,其中实体单元采用四节点平面应变孔隙流体/应力单元(CPE4P),单元总数为22983个; cohesive单元采用四节点黏性孔隙流体/应力单元(COH2D4P),单元总数为45,823个。设置Geostatic与Soils分析步,采用瞬态固结分析,总分析步时间为60s。

3 模拟结果

提取不同层理面强度参数影响下的数值模拟结果,根据二次开发声发射模拟方法获取声发射模拟数据,结合数值模拟结果与声发射数据,得到层理面强度参数对水力裂缝扩展的影响,研讨了层理面强度参数对水力裂缝缝网形成演化的影响。

3.1 裂缝路径和长度

首先提取了不同层理面强度下的裂缝扩展路径(图3)。根据裂缝路径图可知,裂缝从射孔处起裂后,主裂缝沿最大主应力方向扩展。而层理面会阻碍裂缝沿最大主应力方向扩展,由于层理面强度较弱,导致裂缝沿层理面顺层滑移,层理效应明显。层理面较弱时,水力裂缝扩展路径由层理面主导,裂缝直接沿着层理面滑移贯通。随着无因次层理面强度系数的增大,裂缝扩展由层理面主导逐渐转变为层理面和地应力共同作用,破裂方式也由顺层破裂转变为顺层和穿层破裂交互发生的复合破裂类型。当无因次层理面强度系数为1时,层理面对裂缝扩展路径将不起任何作用。此外,顺层破裂裂缝宽度要小于穿层破裂,低缝宽的顺层破裂不利于支撑剂的运移填充。根据裂缝路径可知,当无因次层理面强度系数为0.5时,裂缝扩展路径最复杂,越易产生高缝宽的复杂交错裂缝网络,有利于支撑剂的运移,可实现高效油气开采。

图3 裂缝路径,其中裂缝宽度由颜色表征,从蓝色到红色裂缝宽度逐渐增大

此外,提取了不同层理面强度系数下的总裂纹长度及顺层、穿层裂纹长度(图4),随着强度系数的增大,顺层裂缝长度越来越小,直到强度系数为1时达到0,表明层理面强度越弱,裂缝受层理面的影响越大,裂缝顺层滑移长度越大。总裂缝长度与穿层裂缝长度越来越大,在强度系数为0.75时到达峰值,之后降低。表明层理面的存在有利于裂缝长度的增长,有利于增大裂缝面积,增加油气渗流通道,但是层理面强度参数对水力裂缝的扩展影响并非绝对的,当无因次层理面强度系数为0.5时,可以得到复杂的压裂缝网,当强度系数为0.75时,可得到最大的裂缝长度,而当强度系数再增大到1时,裂缝复杂程度和裂缝长度均劣化。

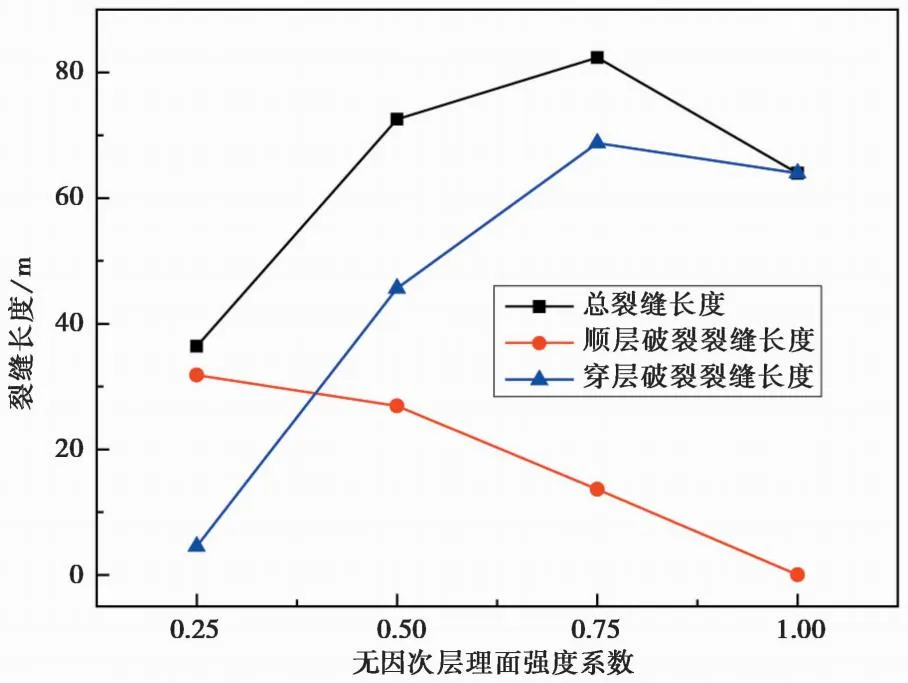
图4 裂缝长度

3.2 声发射定位图和声发射事件数

利用Python编程获取声发射参数,结合Matlab程序实现了AE定位图绘制(图5)。

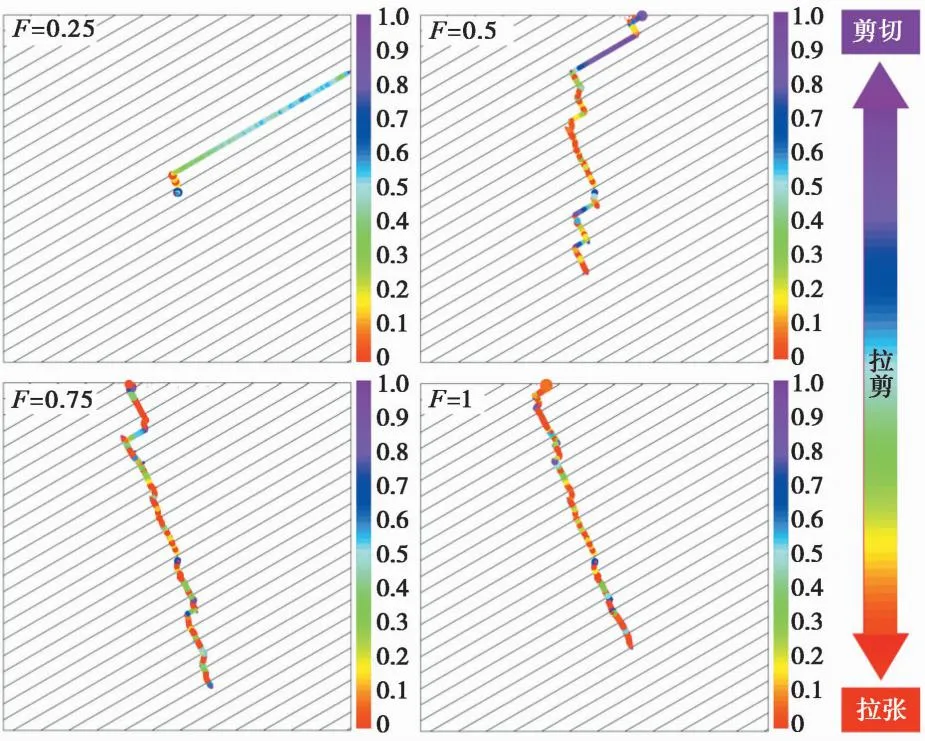
图5 声发射定位图

其中:AE能量和破裂类型分别由AE事件点大小和颜色来表示,红色表示为纯拉破裂,紫色为纯剪破裂,两者之间为拉剪混合破裂。根据声发射定位图可知,整个水力裂缝的扩展过程是拉张破裂和剪切破裂同时作用的结果,顺层滑移破裂总是表现为剪切破裂类型,穿层破裂则为拉张破裂类型。拉张破裂类型的能量要大于剪切破裂类型,并且裂缝在贯通模型边界时,存在大能量声发射事件点。无因次层理面强度系数为0.25时,在射孔下部产生剪切破裂,由于层理面强度较弱,并且在矿物非均质性的影响下,裂缝还没有克服射孔下部强矿物的影响,裂缝就已经沿着层理面滑移贯通,因此在射孔下方没有声发射事件发生。

此外,认定参数MMIXDME值小于0.5时拉张破裂占主导,0.5～1之间为剪切占主导,基于此利用Matlab提取了不同破裂类型的AE事件数(图6)。4种工况下拉张破裂类型AE事件数要明显大于剪切破裂类型AE事件数,拉张破裂占主导地位。随着无因次层理面强度系数的增大,总AE事件数、拉张破裂AE事件数、剪切破裂AE事件数均呈先增大后减小的趋势,即随着层理面强度的增大,破裂事件数逐渐增大,但强度增大到某一值时,则声发射事件数开始减小。强度系数为0.5时的剪切破裂事件数最多,强度系数为0.75的拉张破裂事件数最多。因此,层理面强度太强或太弱,都不利于水力裂缝缝网的产生。

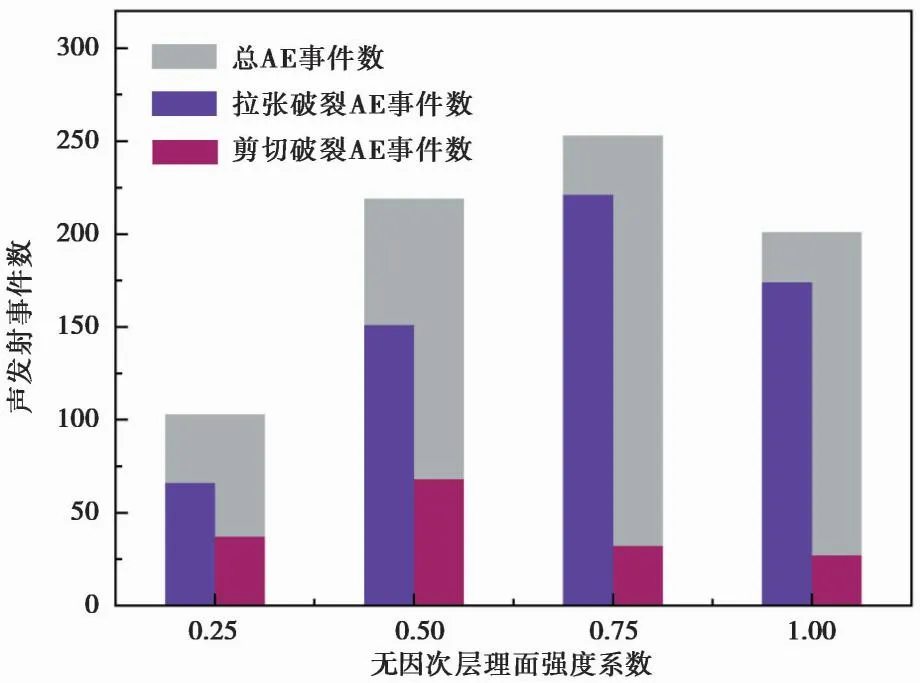
图6 声发射事件数

3.3 孔隙水压力曲线和声发射能量

进一步提取了不同层理面强度的孔隙水压力曲线及整个压裂过程中的声发射能量如图7所示。不同层理面强度下,声发射能量与孔压曲线均表现出相似变化趋势。达到起裂压力后裂缝起裂,开始产生声发射能量,随着压裂的进行,孔压不断增大,裂缝持续扩展,声发射能量分布在整个压裂阶段,直到裂缝贯通,孔压骤降,压裂完成。根据孔压降出现的时间,可以判断层理面强度越弱,裂缝越容易顺着层理破裂贯通,越早出现孔压降。无因次层理面强度系数为0.25时,在压裂初始阶段,存在高能量声发射事件,之后声发射能量趋于平稳,结合图3裂缝路径可以发现,裂缝起裂后主要顺着层理面滑移破裂,所以有较为平稳的声发射能量。强度系数为0.5时,声发射能量在整个压裂过程中分布参差不齐,根据图5声发射定位图可知,穿层破裂声发射能量要大于顺层破裂,因此,高低声发射事件能量的交错分布表明了穿层破裂与顺层破裂的交替发生。在裂缝贯通模型边界时,出现孔压降,同时有高声发射能量的声发射事件产生。

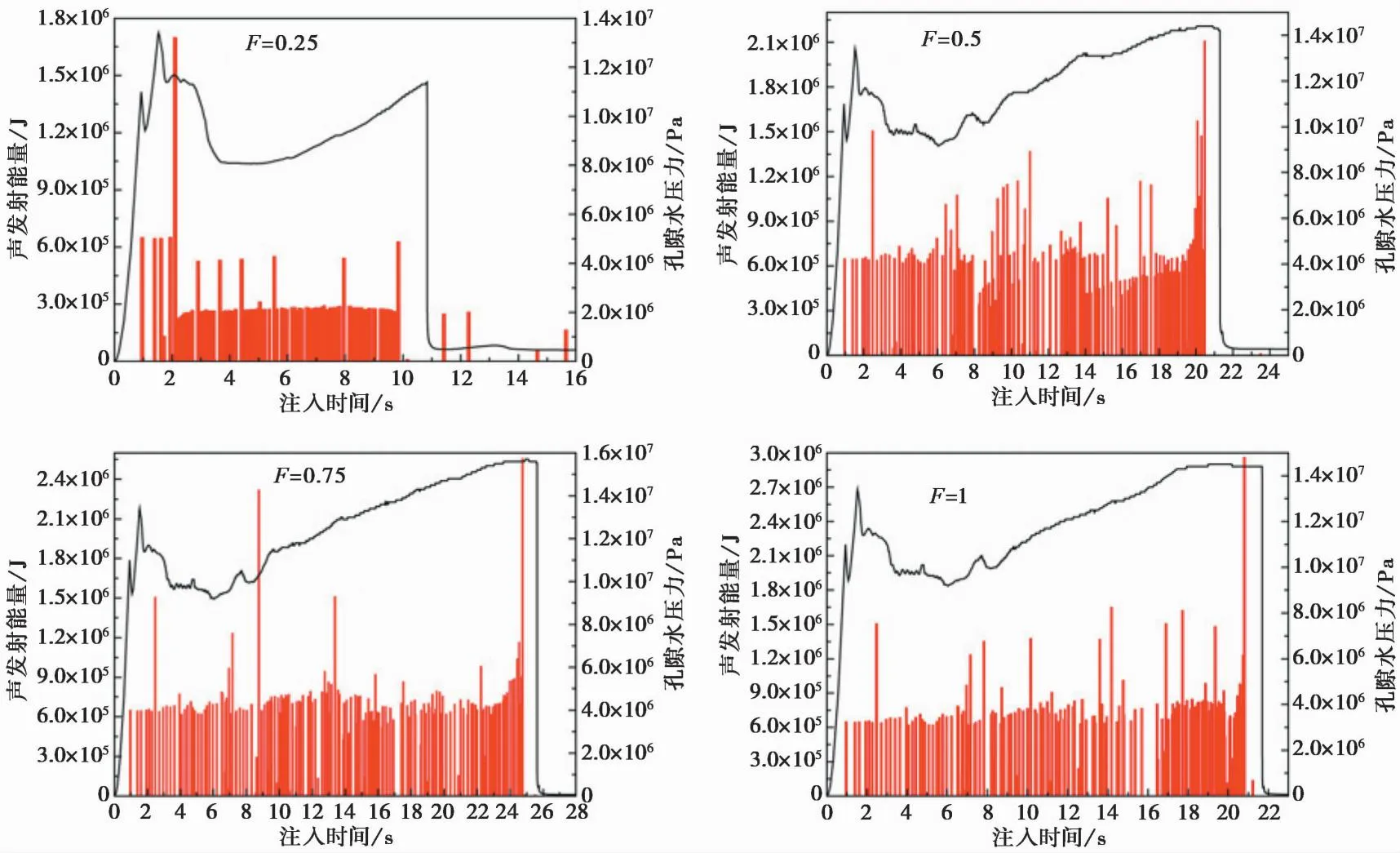
图7 孔隙水压力随时间变化曲线和声发射能量随时间分布图

4 讨 论

4.1 矿物非均质性对水力裂缝扩展影响

由上述研究内容可知在F=0.25时,水力裂缝在射孔上部沿着层理面滑移贯通,射孔下方储层并未开裂。由于本文考虑了岩石的矿物非均质性,因此,认为这种现象是矿物非均质性导致的。为验证这种假设,提取F=0.25时,不同注入时间下流体有效速度矢量云图(图8)。

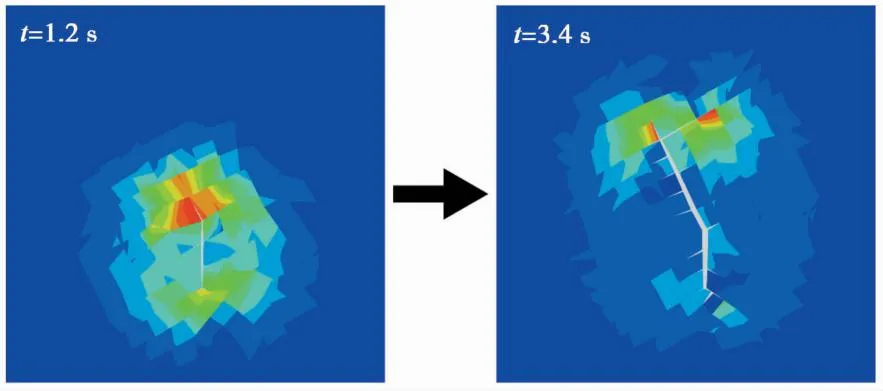
图8 不同时间下流体有效速度矢量云图

由图8可以发现,云图分布存在明显的非均质性。在裂缝开始扩展前,流体有效速度主要集中在射孔上方,促使射孔上部储层开裂; 上部裂缝扩展至层理面后,流速主要沿着层理面分布,而此时流体在层理面内流动更加通畅,导致射孔下部的压力持续减小,更难以开裂。结合图2矿物非均质模型可以发现,在射孔下部存在坚硬石英聚合体,从而导致了该位置储层在一定压力下难以开裂,而随着上部储层的开裂扩展,流体持续向上部汇聚,使得射孔下部更难以达到起裂应力,从而导致了裂缝的非同步性扩展。

4.2 排量对水力裂缝扩展影响

针对矿物非均质性引起的水力裂缝非同步扩展问题,考虑不同排量大小对水力裂缝影响。在F=0.25时,增加最大排量为0.1m2·s-1时的数值模拟结果(图9)。

图9 F为0.25时不同排量下裂缝扩展路径

对比两种排量下的结果可以发现,大排量在一定程度上可以减小矿物非均质性的影响,射孔上下储层均开裂,最终沿着层理面滑移贯通破坏。排量为0.1m2·s-1时,提供了更多的能量可抵抗射孔下部石英聚合体的影响,水力裂缝穿透聚合体,扩展至层理面,从而被层理面捕获。此外,排量越大裂缝宽度越大,越有利于支撑剂的运移。

针对上述F=0.75时的工况,由于此时层理面强度较强,层理面效应较弱,层理作用下的位错缝网较少,考虑从排量控制方式上增加层理面的积极作用。因此,开展两种排量控制方式下的模拟研究,排量控制方式如图10所示。

图10 不同注入速率控制方式

一种为直接加载,另一种为循环加载,即加载至最大排量后,再卸载一定时间,如此往复循环。最终提取两种加载方式下的裂缝路径(图11)。

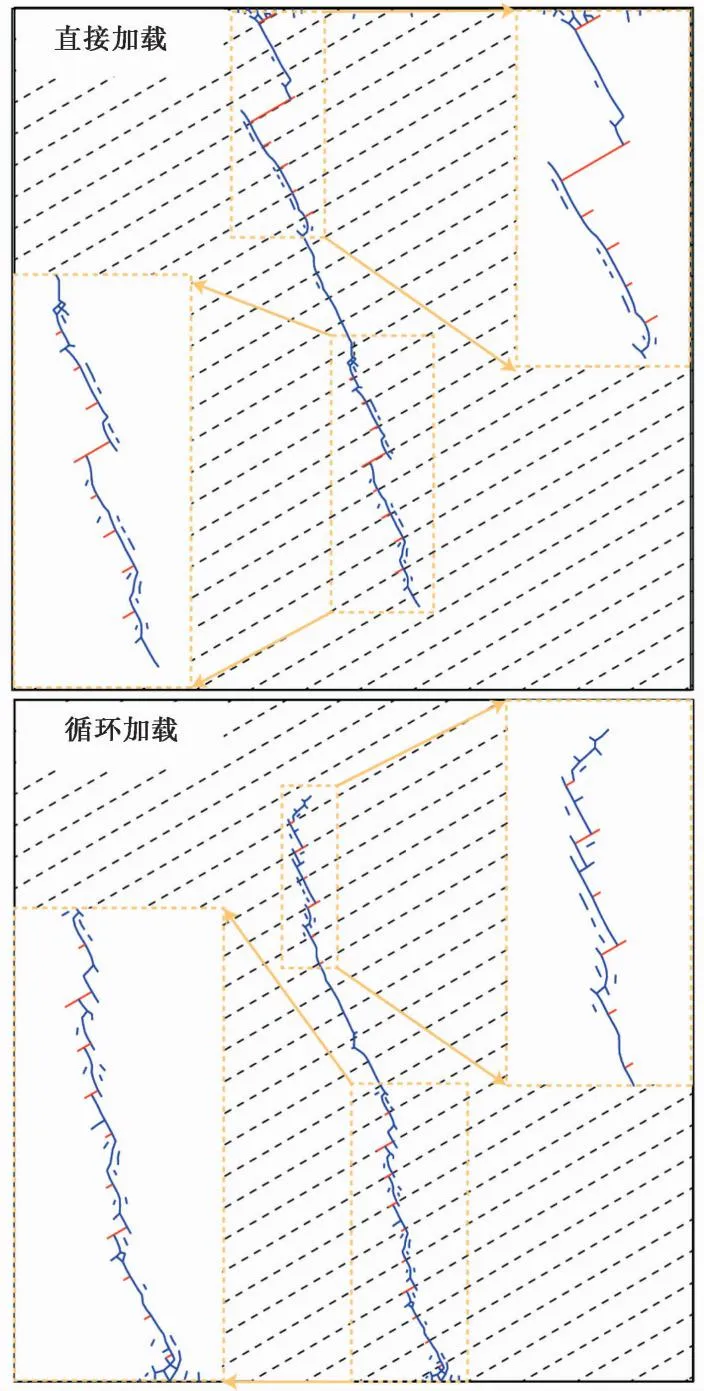
图11 不同注入速率控制方式下裂缝路径

图11中蓝色为穿层破裂,红色为顺层破裂。可以发现,直接加载方式下,由于层理面的软弱性,共有14处层理面被激活起裂,但水力裂缝并没有继续沿着层理面滑移破坏,位错式裂纹只有2处,不利于产生压裂缝网。而在循环加载方式下,共有16处层理面被激活,其中7处小位错滑移裂纹,层理面位错滑移式裂纹的产生充分发挥了层理面的积极效应,有利于产生压裂缝网。此外,循环加载方式下,在主裂缝附近存在更多的次级裂缝,增加了裂缝面积,为油气提供了更多运移通道。

5 结 论

本节采用全局嵌入0厚度cohesive单元的方法,研究了不同层理面强度对水力裂缝缝网演化的影响,结合声发射数值模拟结果,分析了不同层理面强度下的水力裂缝扩展过程,得到以下结论:

(1)最大主应力和层理面均是裂缝扩展的控制因素,最大主应力宏观上决定水力裂缝整体走势,而层理面则会在局部捕获水力裂缝,干扰裂缝扩展方向。并且,层理面越弱,对水力裂缝的捕获能力则越强,裂缝越容易顺层滑移破裂。

(2)矿物非均质性可引起应力非均匀分布,导致水力裂缝非同步扩展,间接增加水力裂缝的复杂程度。

(3)孔隙水压力及声发射能量变化特征可间接表征裂缝扩展情况,声发射能量分布越交错复杂,孔隙水压力曲线越波动,则裂缝路径越复杂。

(4)层理面强度太强或太弱均不利于压裂缝网的产生,层理面强度参数存在最优值,本文中无因次层理面强度系数为0.5时,裂缝扩展路径最复杂,易产生复杂交错裂缝网络,有利于致密油气开采。

(5)根据不同层理面强度破裂特征可针对性的设计压裂方案。对于弱层理面油气储层可适当增大排量以减弱层理面的不利影响。而针对高强度层理面储层可采用循环加压、憋压等方式充分激活天然层理面,增大裂缝网络面积,实现油气高效开采。