页岩气藏高精度地震地层压力预测方法及应用

张入化，王秀姣，石学文，陈 胜，张洞君，杨亚迪，王 鼐

1 中国石油西南油气田公司页岩气研究院；2 中国石油勘探开发研究院

0 前 言

地层压力是指作用于地层孔隙空间流体上的压力，也称地层孔隙压力［1-2］。地层压力既表征了地下油气层的聚集状态，也是油气运移的重要动力［3-4］。压力异常反映了地层的烃源条件、封盖条件以及生烃增压、加热增压、烃类液-气转化增压以及黏土矿物转化增压等各种地质过程。地层压力系数为实测地层压力与同深度静水压力之比。当压力系数等于或接近1 时，即地层压力与静水压力相当，为常压地层；当地层压力小于静水压力时称为低异常流体压力，或简称低压异常；当地层压力大于静水压力时，孔隙流体承受了上覆岩层的部分压力，则称高压或超压地层。

在北美页岩气勘探开发过程中，其地质条件稳定，保存条件良好，储层超压特征不明显，大部分页岩气藏为正常压力甚至低压气藏，地层压力与页岩气产量不存在明显的相关关系，因此，在北美页岩气甜点预测中并没有将储层压力作为一个关键评价指标。中国南方页岩气与北美页岩气的地质背景存在明显差异：中国南方页岩气形成时代较老，经历了多期次剧烈的构造运动，页岩成熟度相对较高，压实作用强烈，储层孔隙度较低。勘探开发实践表明：上扬子区目前已开发的页岩气藏大部分为高压或超压气藏［5］，储层超压特征明显；地层压力越大，测试产量越高，开发潜力越大。因此，准确的地层压力预测，既是保证钻井施工安全以及钻井方法选择的需要，也是甜点预测及井位部署的重要依据［6-8］。

异常高压的形成机理比较复杂，概括起来有：欠压实作用、构造挤压、水热增压、生烃作用、蒙脱石脱水作用、石膏/硬石膏转化、流体密度差异、水势面的不规则性及深部气体充填封存箱的分隔和抬升。在正常压实过程中，随着上覆沉积物的增加，伴随着水的排出和沉积物的压实过程，沉积颗粒之间相互接触，岩石基体支撑上覆岩层的重量，这时的地层孔隙压力等于静水压力。如果由于某种原因造成排水能力减弱，使得本应由骨架承担的压力转移给了孔隙流体，继续增加的上覆沉积物的重量部分由孔隙流体承担，这种情况下则出现欠压实的现象，即异常高压［9］。目前的地层压力预测技术的原理主要基于欠压实作用。地层压力预测方法主要有3 类：钻前预测法、随钻监测法和实测地层压力［10-12］。后两种方法主要基于测井资料来预测地层压力，具有事后性和局部性；钻前预测法主要利用地震资料，预测覆盖面积广，可用资料丰富，可以有效获得研究区内纵、横向的压力展布特征，具有前瞻性和全局性。利用地震资料进行地层压力预测的方法很多，按照孔隙压力计算公式的特点可以分为2 类：①基于正常压实趋势线的方法，如Eaton法［13-14］、Brewer 法［15］、Stoneley 法［16］和 等 效 深 度法［17］等方法。该方法应用的前提是必须根据地层岩性、孔隙度等建立一条由浅至深的正常压实趋势线，但目前正常压实趋势线的建立多依靠研究人员的经验决定。该方法仅适合沉积环境相对简单的连续沉积盆地，对不连续沉积的地层预测结果往往误差较大。②不依赖于正常压实趋势线的方法，该方法以有效应力原理为基础，主要根据地层速度异常判定异常压力的存在，如Bowers 法［18］、Fillippone 法［19］、刘震法［20］和Etminan 法［21］等方法。这类方法避免了正常压实趋势线求取不准所带来的预测误差，公式简单、应用较为方便，但由于其在推导过程中仅用到了地层的纵波速度，忽略了孔隙流体对纵波速度的影响，很容易将流体引起的速度降低当作岩石骨架应力的影响，从而导致预测结果产生较大偏差。

本文在借鉴已有方法的基础上，从岩石力学角度出发引入横波速度，重新推导了有效应力计算公式，克服了储层孔隙流体带来的计算误差，最终建立了由纵波速度、横波速度、密度构成的新的地层压力预测模型，得到了较为准确的地层压力预测结果。

1 地层压力地震预测方法

1.1 有效应力原理

1943 年，Terzaghi 经过多年对饱和多孔介质力学特性的研究，考虑两种力的综合影响，提出了著名的有效应力定理［22］。该理论的基本思想是储层骨架和孔隙流体共同承担上覆地层压力，岩石骨架所承受的重力与有效应力的大小相等、方向相反，在已知上覆地层压力的情况下，只需通过求取垂直有效应力Pe，就可以计算得到孔隙压力Pp：

式中:Pp为地层孔隙压力，MPa；Pov为上覆岩层压力，MPa；Pe为地层岩石垂直有效应力，MPa。

通常，上覆地层压力是储层以上岩石的重力，可作为埋深的线性函数处理，其计算公式如下:

式中：Pov为上覆地层压力，MPa；g为重力加速度，m/s2；H为储层埋藏深度，m；ρ为上覆地层密度，kg/m3；z为深度变量。当上覆地层压力确定时，有效应力越小，孔隙流体所承受的压力越大，储层超压特征越明显；反之，如果地层有效应力越大，即地层的岩石骨架承受了大部分上覆地层压力，则储层孔隙流体承受的压力越小，储层就表现为低压异常。

1.2 基于纵横波速度的地层压力预测法

目前，以有效应力原理为基础的地层压力预测方 法 有 很 多，常 用 的 有Bowers 法［18］和Fillippone法［19］等方法。其中，Bowers 利用垂直有效应力与纵波速度之间的原始加载及卸载曲线方程直接计算垂直有效应力，然后利用有效应力定理基于上覆岩层压力和垂直有效应力确定地层孔隙压力［18］：

式中:Pe为垂直有效应力，MPa；Vi为层速度，m/s；V0为地表或海底速度，m/s；A、B分别为与沉积环境相关的系数，可通过实测压力反算得出。

Fillippone 公式则是根据地层速度直接计算地层孔隙压力［19］：

式中:Pp为地层孔隙压力，MPa；Pov为上覆岩层压力，MPa；Vi为层速度，m/s；Vmax为地层孔隙度为零时的速度，m/s；Vmin为有效应力为零时的速度，m/s。

这类方法利用上覆地层压力和有效应力直接求取地层压力，不需要建立正常的压实趋势线，公式简单、应用较为方便，但同时该类方法在计算过程中仅用到了地层的纵波速度。岩石物理研究表明，纵波速度易受孔隙流体的影响而发生畸变，仅用纵波速度很容易将流体引起的速度降低当作岩石骨架应力的影响，从而导致预测结果产生较大偏差。

Domenico 于1977年所做的岩石力学实验表明，有效应力与纵、横波速度间存在密切联系［23］。地震岩石物理研究表明：流体中横波速度为零，横波速度只与岩石骨架有关。因此，本次研究中引入横波速度，重新推导了地层压力计算公式，有效表征岩石应力。根据广义胡克定律可知：

式中:K为岩石骨架体积模量，MPa；Pe为岩石骨架有效应力，MPa；ΔB/B为单位体积岩石压缩量。于是：

根据波动方程可知纵、横波速度与岩石力学参数间存在如下关系：

式中:Vp、Vs分别为岩石的纵波速度、横波速度，m/s；K为岩石骨架体积模量，MPa；μ为岩石剪切模量，MPa；ρ为岩石密度，kg/m3。由公式（7）、（8）可知体积模量与纵、横波速度间存在如下关系：

由于在盆地正常沉积压实过程中，地层横向应变远远小于纵向应变，因此单位体积应变量可用单位厚度的应变量代替，于是将公式（9）代入（6）可得：

这里，利用孔隙度变化梯度近似表征单位厚度压缩量，即：

式中：θor为深度H处的孔隙度，%；θ0为地面处的孔隙度，即临界孔隙度，%。将公式（2）、（10）、（11）代入（1），最终得到了新的地层压力计算公式：

式中:Pp为地层孔隙压力，MPa；g为重力加速度，m/s2；ρ为上覆地层密度，kg/m3；z为深度变量；Vp、Vs为岩石的纵波速度、横波速度，m/s；H为储层埋藏深度，m；θor为深度H处的孔隙度，%；θ0为地面处的孔隙度，即临界孔隙度，%。

利用纵波速度、横波速度、密度及临界孔隙度构建了新的地层压力计算公式，其中纵波速度、横波速度、密度可通过地震叠前反演获得，临界孔隙度则根据储层岩石物理建模得到。Nur于1992年提出临界孔隙度模型，该模型指出对于大多数岩性稳定、矿物成分相对稳定的岩石，都有一个相对固定的临界孔隙度［24］。当岩石孔隙度小于临界孔隙度时，岩石压实成岩，矿物颗粒相互接触传递有效应力；当岩石孔隙度大于临界孔隙度时，矿物颗粒间相互分离，主要通过孔隙流体传递有效应力。基于临界孔隙度，Nur 提出了岩石骨架与固体基质弹性模量之间的关系［24］：

式中:Kdry为岩石骨架的体积模量，MPa；μdry为岩石骨架的剪切模量，MPa；Kma为固体基质的体积模量，MPa；μma为固体基质的剪切模量，MPa。固体基质的体积模量和剪切模量可由各矿物组分的体积模量和剪切模量根据Voigt-Reuss-Hill 近似模型计算得到，孔隙度θor利用多矿物最优化算法求取，Kdry、μdry则在已知孔隙度和固体基质模量的情况下，应用Krief模型［25］求取。最后，基于以上已知量根据公式（13）、（14）求取临界孔隙度θ0。

由于横波速度不受孔隙流体的影响，更能反映岩石骨架的成分和有效应力，本文中新推导的公式在求取有效应力的过程中加入了横波速度，可以有效改善有效应力计算精度，提高地层压力预测精度。

2 实际应用效果分析

2.1 研究区概况

四川盆地总面积约为26×104km2，是中国常规天然气探明储量及累计产量最多的盆地之一，也是目前中国页岩气探明储量和产量最丰富的盆地［26］。LU208 井区位于重庆市荣昌区，工区地表为丘陵地形，地貌以低山深丘为主，平均海拔为300～400 m。研究区构造位置隶属于川南低陡构造带，目的层上奥陶统五峰组—下志留统龙马溪组埋深为2 300～3 800 m，区内发育系列断背斜，背斜隆起区构造相对窄陡、断层较发育，向斜区构造相对宽缓，整体呈现出洼隆相间的构造格局（图1）。

图1 LU208井区上奥陶统五峰组底界构造图Fig.1 Structure map of the bottom of the Upper Ordovician Wufeng Formation in LU208 well area

研究区地层发育齐全，自下而上发育前震旦系变质岩、震旦系—中三叠统海相沉积岩以及上三叠统—白垩系陆相碎屑岩。下志留统下部发育龙马溪组优质页岩，与下伏上奥陶统五峰组灰黑色页岩、泥灰岩整合接触，上部为石牛栏组灰绿色、黄绿色、浅灰色砂岩或泥页岩（图2）。龙马溪组总体以黑色、灰黑色碳质、泥质和粉砂质页岩为主，地层厚度为350～650 m，分布稳定，发育水平层理、交错层理，含大量笔石化石；页岩有机碳含量高，优质页岩厚度大，是现阶段页岩气勘探开发的有利目标层系。

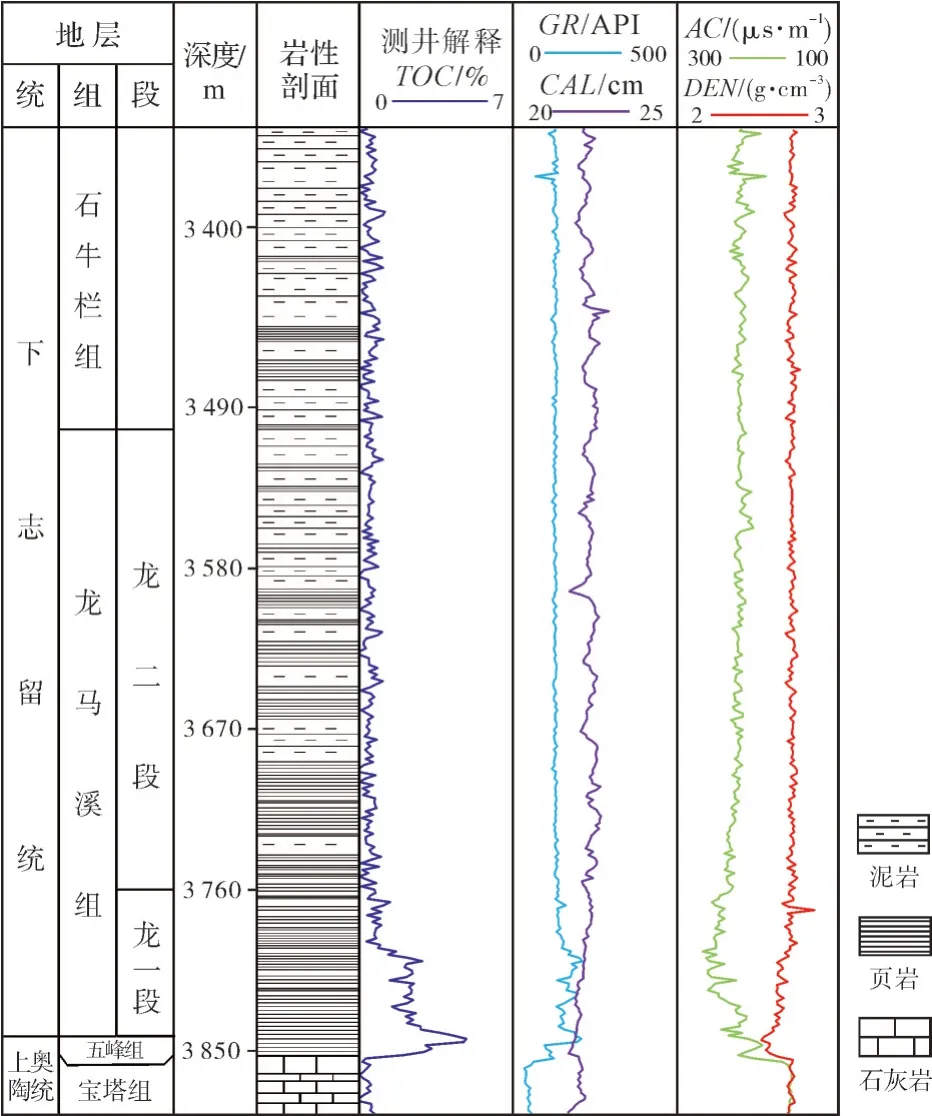
图2 LU208井区下志留统龙马溪组地层综合柱状图Fig.2 Comprehensive stratigraphic column of the Lower Silurian Longmaxi Formation in LU208 well area

图3 页岩地层压力预测流程图Fig.3 Workflow of formation pressure prediction for shale

根据岩性和测井响应特征，将龙马溪组划分为龙一段和龙二段（图2）：龙一段发育黑色、深灰色页岩，TOC较高，测井曲线呈低声速、低密度、高伽马的特征；龙二段以灰色、深灰色、灰黑色泥岩为主，夹少量薄层粉砂岩、石灰岩和页岩，页理不发育，TOC低，测井曲线呈较高声速、较高密度、较低伽马的特征。龙一段下部—五峰组优质页岩段，主要由黑色碳质、硅质页岩组成，含大量的笔石生物群，页岩层理发育，声速和密度较低，TOC一般在2%以上（图2），是本次研究的主要目的层段。

2.2 研究思路

首先，基于地震、测井解释资料进行岩石物理分析，确定页岩储层岩石物理特征。然后，应用钻井、三维地震资料，进行叠前弹性参数反演，预测目的层段的速度、密度等关键弹性参数的空间分布。最后，结合井-震标定结果，将地震数据和反演得到的数据体转换到深度域，通过建立由纵波速度、横波速度、密度构成的新的地层压力预测模型，实现了页岩地层压力定量预测。

2.3 叠前反演

页岩储层关键评价参数数据体均基于地震弹性参数反演获得，反演结果的准确性是预测地层压力的关键。目前，常规的叠前反演技术主要是基于叠前时间/深度偏移的CRP道集数据，通过使用不同的Zoeppritz方程近似式，直接反演或求解得到不同的弹性参数反射率。其中，最常用的是Aki-Richards公式［27］：

式中:Rpp为纵波反射系数；i为入射角；Vp、Vs分别为纵波速度、横波速度，m/s；ρ为密度，kg/m3；ΔVp、ΔVs、Δρ分别为纵波速度、横波速度、密度变化量。在常规的求解过程中，往往假定Vs/Vp为常量，将公式进一步简化为线性近似式求解。但由于这种线性近似，往往影响了反演结果的可靠性和预测精度，这里，本文采用量子蒙特卡洛方法［28-29］直接进行非线性反演，不再将Vs/Vp视为常量。此外，随着入射角度增大，ΔVp/Vp、ΔVs/Vs、Δρ/ρ的系数变化差异较大，ΔVs/Vs和Δρ/ρ的系数变化量远小于ΔVp/Vp。这种系数项随入射角变化趋势的不同造成了方程求解过程中的奇异性，导致弹性参数反演精度不同：纵波速度反演精度较高，横波速度与密度反演误差较大。研究中为有效均衡系数项引起的响应差异，提高反演精度，引入了加权系数λx：

式 中：λx=CxM/Mx。其 中，Mx分 别 为ΔVp/Vp、ΔVs/Vs、Δρ/ρ的系数项；M为系数项之和；Cx为系数调节因子，无量纲。通过引入加权系数，对各系数项进行均衡，改善求解过程中各参数的响应敏感度，提高叠前反演的预测精度。

图4 为叠前反演得到的纵波阻抗、横波阻抗和密度预测结果，可以看出优质页岩段表现为明显的低纵波速度、低横波速度和低密度特征。

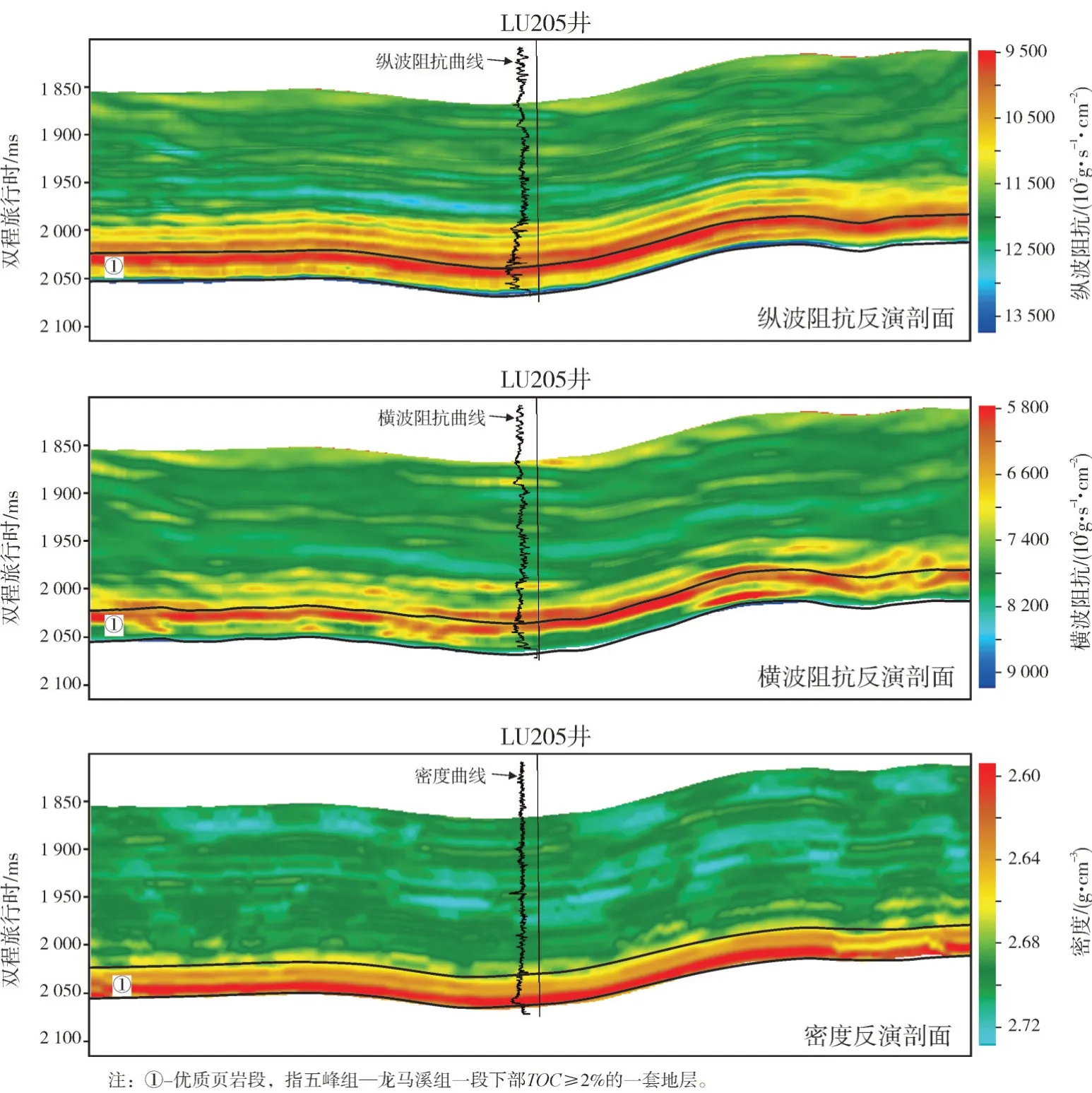
图4 过LU205井的叠前反演剖面（剖面位置见图1）Fig.4 Pre-stack inversion profile calibrated by Well LU205(profile location is shown in Fig.1)

2.4 地层压力预测

基于叠前反演得到的纵波速度、横波速度和密度数据体，应用本次研究推导的地层压力预测公式，最终得到地层压力预测数据体。图5 是地层压力预测剖面，可见优质页岩段地层压力整体偏高，压力系数整体在2.15以上，高压异常明显。

图5 过LU205井地层压力反演剖面（剖面位置见图1）Fig.5 Inversion profile of formation pressure crossing Well LU205(profile location is shown in Fig.1)

图6 为优质页岩段平均地层压力预测平面图，其中暖色调代表地层压力高值区，冷色调为地层压力低值区。对照构造图（图1）分析，平面上地层压力受构造及断裂作用影响：背斜部位断层发育，压力容易释放造成地层压力偏低；向斜部位地层压力偏高，意味着储层含气性较好，保存条件优越，是有利的页岩气开发区带。

图6 LU208井区优质页岩段地层压力预测平面图Fig.6 Plan of predicted formation pressure of the high quality shale section(lower part of Longmaxi Formaiton-Wufeng Formation)in LU208 well area

为了进一步验证新方法的有效性和预测结果的准确性，将工区内4 口有实测压力值的井与地震预测结果进行了误差统计。对比结果（表1）表明：地层压力预测结果与实际测井解释结果误差较小，4口井的平均误差为4.71%，吻合程度较高。本文的地层压力预测方法以地层压实理论为基础，充分考虑了速度对地层压力的影响，应用高精度的叠前反演算法准确求取速度和密度，从而提高了压力预测精度。由于形成地层超压的原因是多方面的，除压实成因外，还有水热增压作用、构造作用、蒙脱石脱水作用等因素，对于非压实成因的地层压力预测此方法不适用。

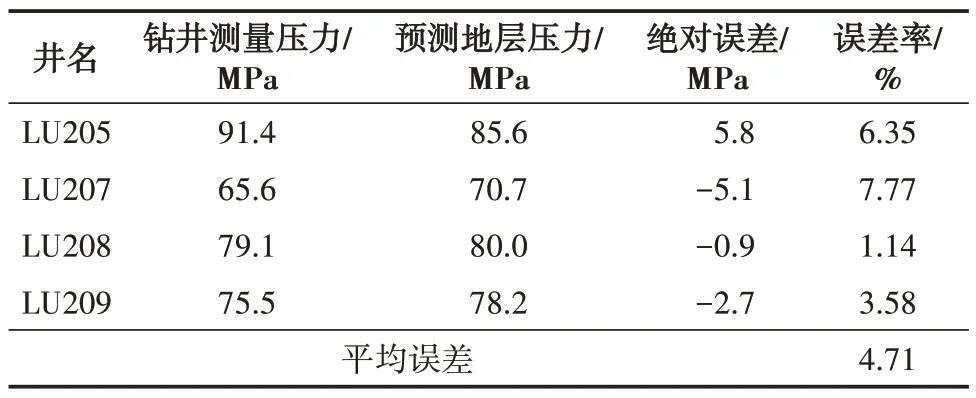
表1 LU208井区地层压力预测结果与钻井实测结果对比Table 1 Comparison of formation pressure prediction results and drilling measurement results in LU208 well area

3 结 论

中国南方海相页岩气勘探开发实践表明：页岩气储层地层压力与产量之间存在明显的正相关关系，地层超压是页岩气高产的必要条件。地层压力预测对页岩气大规模高效开发具有重要意义。本次研究以地质力学的有效应力原理为基础，引入横波速度，推导了新的地层压力计算公式，建立了由纵波速度、横波速度、密度构成的新的地层压力预测模型。该方法在川南地区LU208井区五峰组—龙马溪组海相页岩气勘探中得到有效应用，预测结果具有较高的准确性和适应性。研究结果对我国南方海相页岩气甜点预测和钻井部署具有重要意义。