漫谈无理数的“那些事”
文/江苏省无锡市梅里中学 朱嘉颖
数学源于对真实问题的思考,离不开善于观察的慧眼。数从自然数走向小数,从正数走向负数,从有理数走向实数的漫长过程中,我们与无理数相遇了。
无理数的“真面目”
我们知道,无理数是无限不循环小数。我们还能在数轴上找到表示无理数的点。比如,我们可以在数轴上方画一个Rt△ABC,点A在原点处,点B在数轴1 的位置,AB=BC=1。在Rt△ABC中,AC2=2,AC=。以原点为圆心,AC长为半径作圆弧,与数轴正半轴的交点即为所求的(如图1)。
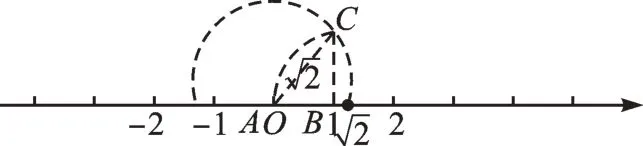
图1
观察数轴,我们可以发现1<<2,那么到底是多少呢?我们可以通过不断尝试大于1 且小于2 的数,逐渐接近的精确值。在数学中,不断缩小取值范围可以通过“二分法”实现。我们先取1 与2 的中间值1.5,因为1.52=2.25>2,所以1<<1.5。接着试1 与1.5 的中间值1.25,因为1.252=1.5625<2,所以1.25<<1.5。为了运算的简便,我们不妨尝试计算1.3,因为1.32=1.69<2,所以1.3<<1.5。接下来我们尝试1.4,因为1.42=1.96<2,所以1.4<<1.5。以此类推,的取值范围不断精确,最后,我们可以推得≈1.414。如果有兴趣的话,你可以继续用“二分法”来尝试确定、的大小。
无理数“PK记”
既然无法精确表示无理数的值,我们该如何比较无理数的大小?如和。
取中间值法、平方法、数轴法,我们可以从“数与形”两个角度,比较两个无理数的大小。
无理数的“分割术”
方法二,用“形”:在数轴上把表示3 的点画出来。我们知道3 无法表示为一个两条直角边都是正整数的直角三角形的斜边,所以我们只能逆向思维,表示为一个一条直角边为1、斜边为2 的直角三角形的另一条直角边。如图2,AB=1,用圆规在数轴上截取AC=2,则BC=。观察可知,的整数部分是1,则小数部分是-1。

图2
显然用“数”的方法,我们可以更快地将无理数进行“分割”。
无理数的“应用界”
当然,无理数还有很多的妙用。在数学中,我们可以在方格纸中画一个三条边长都是无理数的三角形;在生活中,普遍应用于艺术设计、建筑设计等领域的黄金分割比也是个无理数……
我相信,只要我们拥有一双善于发现的眼睛,一定可以发现更多与无理数相关的“故事”。
教师点评:
小作者用数学的眼光发现问题、提出问题,从有好奇心走向数学思考,进而分析问题、解决问题。我们的数学学习始于好奇,精于思考,成于坚持。让我们像科学家一样思考,不断提高自己的数学思维能力。

