基于CNN-CA 模型的地表覆盖变化模拟

孔凡强，刘柄宏，葛潇钦，王品源，张清琪

（1.浙江省测绘科学技术研究院，浙江 杭州 310000 ；2.绍兴市上虞区自然资源监测中心，浙江 绍兴 312000）

0 引言

地表覆盖数据具有全覆盖、无缝隙、无重叠、种类繁多等特征。它的预测对产业、人才布局具有重要影响。早期研究一般仅对地表覆盖各地类相互转化总量进行预测，比较常用的模型是马尔可夫模型[1]，它将地表覆盖变化看作以年为单位的离散过程，且每年的转化率相等，以此预测地表覆盖数据。随着计算机技术的发展，元胞自动机开始被引入该领域[2-3]，从邻域出发预测中心单元的变化规律。土地地类的转化仅与邻域相关，这与地理角度中的距离相关性不谋而合。这种方法取得了较好效果，随之也带动了矢量元胞自动机的发展[4]。但元胞自动机局部驱动土地变化，导致预测转化总量会与实际差距较大，因此，CAMarKov 方法成为了主流方法。它将马尔可夫模型与元胞自动机相结合，具备总量控制与局部驱动的双重优势[5-6]，进一步提升预测精度。鉴于元胞自动机的参数确定存在人为主导的缺陷，许多学者结合元胞自动机与客观方法研究地表覆盖变化，如遗传算法[7]、支持向量机[8]、系统动力学[9]、深度学习[10]等，通过已有的样本预先训练确定相关参数，进而预测未知的数据。这使得地表覆盖变化预测方法进一步完善，精度越来越高。

综上所述，地表覆盖变化情况复杂，影响因子多，单一方法难以准确模拟。地表覆盖变化受邻域状态变量和邻域空间分布状态的影响，元胞自动机无法实现通过邻域状态模拟复杂系统。基于此，本文采用卷积神经网络-元胞自动机模型（CNN-CA），利用卷积神经网络提取元胞的邻域空间分布特征[11-12]，通过元胞自动机提取元胞的邻域状态特征，组合空间分布特征与状态特征并模拟地表覆盖变化。本文利用6 种卷积核和采样窗口组合搭建神经网络结构，分别模拟地表覆盖变化，并对模拟结果的生产者精度（PA）、用户精度（UA）、总体分类精度（OA）和Kappa 系数4个指标进行计算，分析卷积核与采样窗口大小对卷积神经网络计算质量的影响。CNN-CA 模型能够顾及元胞空间分布特征，可以进一步提高CA 模型的模拟应用能力。

1 地表覆盖CNN-CA 模型

CNN-CA 模型充分发挥卷积神经网络和元胞自动机的优势，通过卷积神经网络计算各单元向各地类的转化概率，并顾及元胞邻域状态，建立了模型框架，如图1 所示，该模型框架包括输入数据、卷积神经网络、元胞自动机、模拟输出4个部分。选取11 个影响因子作为输入数据，对矢量数据进行栅格化，保持各个影响因子栅格单元的尺寸和坐标一致。通过模拟区域的界线提取栅格数据掩膜，形成一组范围相同、行号和列号相等的数据。为了加快神经网络训练速度并保持各个特征的相同维度，还需要对栅格数据进行标准化处理，即每个单元格数值除以该层数据的最大值，使栅格数据范围为0～1。模型搭建的卷积神经网络包括2 个卷积层和2 个池化层；通过全链接层输出转化概率。元胞自动机用于计算元胞邻域状态空间，通过状态空间计算元胞向每种地类的转化概率。融合2 个模型计算概率并计算最终元胞的转化方式。依据CNN-CA 模型结构，元胞向各个地类转化的概率计算方法如公式（1）所示，随机约束计算方法如公式（2）所示。

图1 CNN-CA 模型框架

式中：Pm为元胞向m地类转化的概率；为卷积神经网络计算的元胞（i，j）向m地类转化的概率；为元胞自动机计算的元胞（i，j）向m地类转化的概率，即中心元胞邻域m地类占邻域的比例，若元胞邻域不存在m地类，则Pm为0，这种情况与实际不相符，因此本文在占比的基础上加0∙5；为元胞（i，j）向m地类转化的随机约束；a为0～1 的随机数；k为控制随机强度的参数，本文令k=2。

2 CNN-CA 模型应用分析

2.1 研究区

本文研究区位于浙江省绍兴市上虞区的曹娥街道和百官街道，地处浙江省绍兴市东北部、钱塘江南岸，拥有高速公路、高铁、铁路、港口、运河等基础设施。近几年，研究区的经济、农业、工业、商业产值均稳步提升，地表覆盖变化较明显。因此，本文以研究区为试验区验证模型的准确性。

2.2 数据来源和处理

本文试验数据均来自浙江省地理国情监测项目，其中，2017 年、2019 年、2021 年原始地表覆盖数据是1：1 万矢量数据。本文将三级地类转化为二级地类，研究区包括林草覆盖、种植植被、房屋建筑（区）、铁路与道路、构筑物、堆掘地表、水域7 种二级地类。将矢量数据转化为20 m×20 m 栅格数据；将5 m 分辨率数字高程模型（DEM）重采样为20 m 分辨率地形数据，由DEM 数据计算生成坡度、坡向数据；利用空间矢量数据计算距农村道路距离、距公路距离、距城市道路距离、距高铁距离、距普速铁路距离、距行政中心距离、距便民中心距离的欧式距离并按1 000 m 分级别的栅格作为影响因子，选取区政府和乡镇政府驻地为行政中心，以学校与医院2 个类型计算便民中心。

2.3 参数确定与模型训练

卷积神经网络采样窗口与卷积核的大小对模拟结果影响很大。本文在其他参数保持不变的情况下，采用9×9、17×17、23×23 采样窗口与3×3、5×5 卷积核的两两组合试验，形成6 种网络结构。6 种网络结构都是3 层结构，第一个卷积层采用55 个卷积核，第二个卷积层采用275 个卷积核，第三个卷积层采用1 375 个卷积核，每个卷积层后接入一个2×2 的最大值池化层压缩数据。为保证输入与输出图像一致，模拟前需对各个栅格数据进行扩展。网络最后的全连接输出层神经元有7 个，对应7 种不同的地表覆盖类型。本文以研究区2017—2019 年地表覆盖变化情况为整体样本，通过采样窗口共获取212 790 个样本；神经网络训练时将batch 设置为30，即每次对30 个样本进行训练；将epoch 设置为15，即总体样本循环训练15 次；采用交叉熵损失函数，通过梯度下降法优化网络结构，不同网络结构的运行效率如表1 所示。

表1 不同网络结构的运行效率

由表1 可知，采样窗口大小和卷积核大小都与训练时间成正比。卷积核变大时需要计算的参数增多，每个5×5 卷积核比3×3 卷积核多16 个偏移参数和16 个权重参数；采样窗口变大时参与运算的栅格数量增多，所花费时间也增多；模拟时间同理，模拟时间仅执行1 次运算，所以时间增加幅度小。另外，由训练集精度可知，采样窗口和卷积核的尺寸不是越大越好，尺寸过大会导致参与运算的范围变大、冗余数据变多，产生过拟合的问题。9×9 采样窗口、5×5 卷积核网络的训练集精度最高，9×9 采样窗口、3×3 卷积核网络的执行速度最快，23×23 采样窗口、5×5 卷积核网络的执行速度和训练集精度均最低。

元胞自动机采用5×5 扩展莫尔型邻域为模拟范围，计算邻域状态对元胞变化的影响。

2.4 试验结果与分析

本文利用6 个不同的CNN-CA 模型对研究区进行模拟。选取生产者精度、用户精度、总体分类精度和Kappa 系数4 个评价指标进行模型评价。生产者精度表示某类别真实数据被正确分类的概率；用户精度表示落在某类别的检验点被正确分为该类别的比例；总体分类精度表示所有正确分类的数量占总数的百分比；Kappa 系数用于分类的一致性检验，数值范围为0～1，Kappa 值越大表示分类精度越高，一般75%以上的Kappa 值表示分类精度及可信度较高。计算方法如公式（3）～（6）所示。

式中：PAi表示i地类生产者精度；Ni表示i地类正确分类的数量；Oi表示真实数据中i地类的总数；UAi表示i地类用户精度；Mi表示模拟数据中i地类的总数；OA表示总体分类精度；A表示正确分类的土地数量；Z表示总体土地数量；Kappa表示Kappa 系数；PO表示模拟正确的栅格数量占栅格总数的比例，为观察一致性；PC为期望一致性。

生产者精度与用户精度用于评价单一地类的模拟精度，总体分类精度与Kappa 系数用于评价总体的模拟精度。计算模拟结果与2021 年地表覆盖数据的混淆矩阵，通过混淆矩阵计算6 个网络模型的4 个评价指标。

模拟精度评价指标如表2 所示，模拟精度与训练集精度类似。各地类模拟精度与总体精度的采样窗口和卷积核尺寸都不是越大越好。6 种网络结构的总体分类精度均达83%以上，除堆掘地表和铁路道路的单个地类模拟精度达73%以上且大部分模拟精度高于85%，表明模型模拟精度很高；Kappa 系数均达79%以上，表明模拟结果一致性较好。以上结果说明，模型对地表覆盖变化预测具有一定的可靠性，总体上各个地类的模拟都达到了比较满意的效果。9×9 采样窗口、5×5 卷积核网络在各项指标中脱颖而出，除堆掘地表外指标精度都达90%以上，模拟效果最好。在9×9与17×17 采样窗口中，5×5 卷积核的模拟精度总体比3×3 卷积核的模拟精度更高；在23×23 采样窗口中，卷积核的尺寸与模拟精度没有一定关系。这说明采样窗口变大导致冗余数据增多，难以通过卷积核尺寸控制模拟精度，过大的采样窗口不适于地表覆盖变化模拟。基于CNN-CA 模型的铁路与道路指标模拟精度最高，9×9 采样窗口、5×5 卷积核网络的铁路与道路生产者精度和用户精度分别达到0∙982 和0∙992，这是因为铁路与道路具有变化周期长、分布稳定的特点。堆掘地表的6 种网络结构模拟均处于较低水平，其中，生产者精度约60%，用户精度基本处于40%以下。在地理国情监测分类中，凡是有堆积物的地表都被划为堆掘地表，难以通过特征模拟其变化规律，这最终导致卷积神经网络模拟精度低。

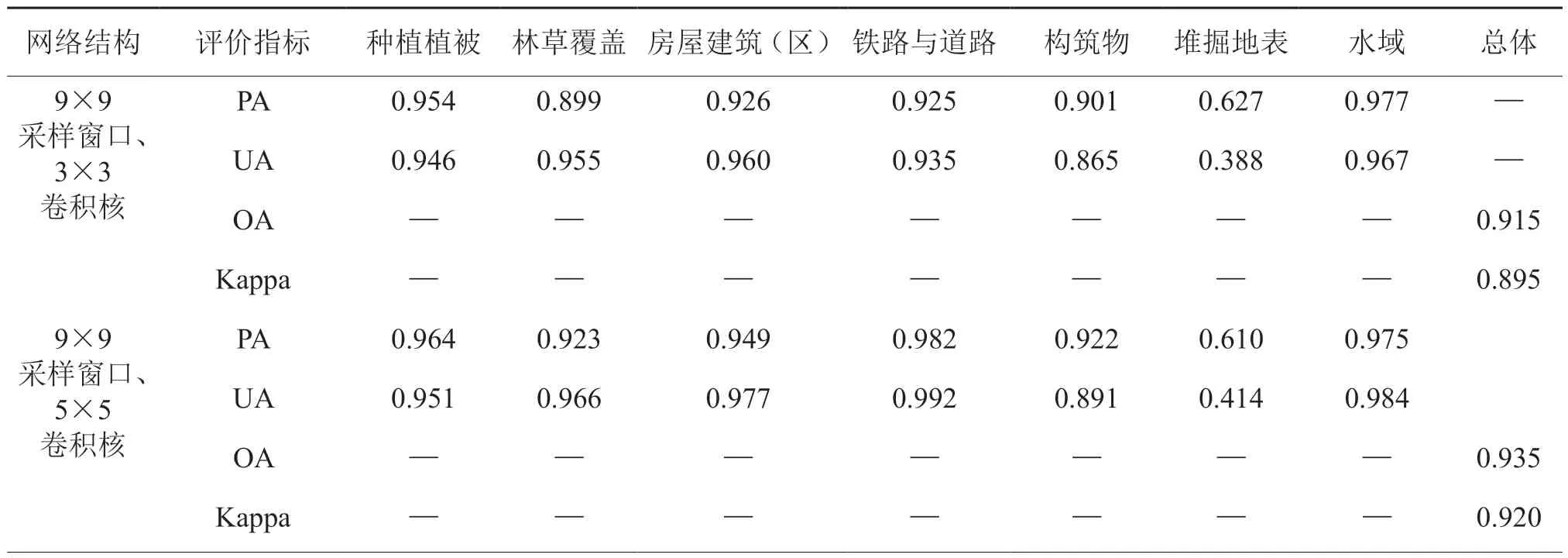
表2 模拟精度评价指标

3 结论

本文采用的卷积神经网络-元胞自动机模型，在传统元胞自动机模型的基础上加入卷积神经网络，将元胞邻域的空间分布特征作为影响因子并纳入计算。利用6 种不同网络结构对研究区地表覆盖变化进行模拟，对比分析不同卷积核和采样窗口对模拟结果质量的影响。研究结果表明，地表覆盖变化模拟卷积核和采样窗口的尺寸不是越大精度越高，而是由实地特点确定。此外，本研究对模拟结果进行多个指标评价，讨论了不同地类模拟精度的原因。结果表明，CNN-CN 模型在地表覆盖变化模拟中的总体分类精度和单一地类模拟精度较高，且模拟效果的一致性较好。因此，该模型能够较好地模拟地表覆盖变化，在该领域具备一定的指导作用。

本文对于人为定义超参数的测试较少，如网络层数与网络学习率，这将是后续研究的重点内容。