航空发动机涡轮叶片疲劳寿命预测和可靠性分析

马 雄，李 翠，杨 飘

(贵州民族大学数据科学与信息工程学院，贵州贵阳)

引言

目前，我国航空发动机的叶片材料主要分为变形耐高温合金、铸造高温合金、超塑性成形钛合金、金属间化合物和新型材料五类，其中最常见的航空发动机叶片材料是变形高温合金，已有50 多年的历史。我国的军用航空发动机叶片材料以K465、K4002、DZ125、GH4033、GH4037 为主。孙宇博利用Paris 公式为理论依据，结合不同应力水平作用下疲劳裂纹扩展速率及尖端强度因子的变化，建立振动试样剩余寿命计算模型，通过振动疲劳试验测得结果对数值模型计算的可靠性进行验证[1]。李福以材料GH4037 为研究对象，获取微观组织参数以及材料数据，进行归一化分析处理。分析隐含层数、隐含层节点数、学习效率、训练目标、传递函数、训练函数等对BP 网络模型建立的影响[2]。一些人建立基于材料GH4037 数据的优化BP 网络蠕变寿命分析模型，获取微观组织蠕变剩余寿命，为蠕变寿命可靠性分析提供模型[3]。

本文以常温下GH4033 型涡轮叶片作为研究对象，首先对试验数据进行正态性检验，基于应力-寿命试验数据建立SN 曲线，然后引入概率P（存活率），绘制P-S-N 曲线。其次，根据安全系数K 和应力-强度干涉模型，在符合工程要求的可靠度下，对强度参数进行极大似然估计，从而得到航空发动机涡轮叶片的强度。

1 GH4033 合金材料疲劳试验

以GH4033 为材料的合金主要以镍-铬合金为基体，主要用做航空发动机的涡轮工作叶片，在700～750 ℃仍然能够保持足够的高温强度，是国内外航空发动机涡轮叶片常使用的合金材料之一。

GH4033 合金的化学成分及力学性能如表1、表2所示[10]。

表1 GH4033 合金化学成分

表2 GH4033 室温下力学性能

林杰威根据国家标准GB/T 228－2002，设计了圆棒拉伸试验[11]。此标准适用于本文的20 ℃空气条件下，测定GH4033 合金圆形横截面试样在旋转状态下承受弯曲力矩时的疲劳性能。试验结果如表3 所示。

表3 室温下GH4033 疲劳试验数据

从试验数据中可以发现，随着等幅降低应力，试件的疲劳寿命在增长。试件6 在载荷550 MPa，循环次数为3×107下，也未发生疲劳破坏。再增加循环次数或降低载荷，GH4033 材料也不会发生疲劳破坏。因此，负载550 MPa 对应的循环次数3×107，便是GH4033 的疲劳极限。但有些试件的寿命不知道，可以使用线性插值来估算缺失值，如表4 所示。

表4 线性插补后的GH4033 应力- 寿命数据

试验数据的正态性检验：

首先，我们对这两组数据取对数，然后采用Shapiro-Wilk 方法对应力数据进行正态性检验。显著性水平取值为0.05，假设检验为：

H0:这两组数据服从对数正态分布;

H1:这两组数据不服从对数正态分布。

利用Shapiro-Wilk 检验得到的结果如表5 所示。

表5 Shapiro-Wilk normality test

2 P-S-N 曲线下的疲劳寿命预测

前面，已经得到了室温下GH4033 的疲劳试验数据，此时就可以画出叶片材料GH4033 的S-N 拟合曲线，如图1 所示。

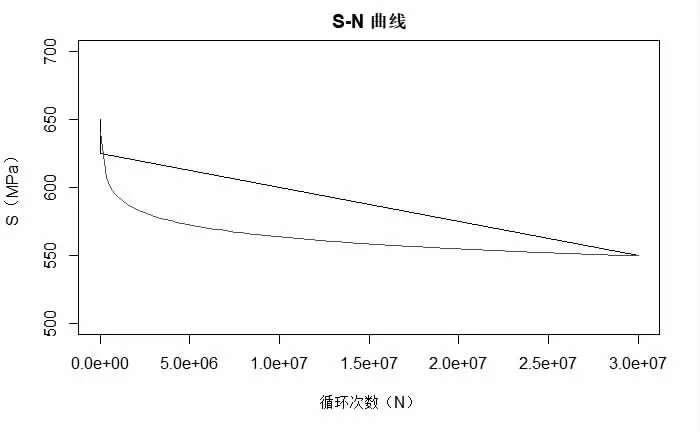
图1 室温下GH4033 材料的S-N 曲线

Weibull 分布：

非负随机变量寿命T 服从Weibull 分布，T 的失效密度函数为

对应的寿命分布函数为

失效率函数为

可靠度函数为

由表5 可知，应力数据经过Shapiro-Wilk 检验的P 值大于0.05，说明原假设成立，应力这组数据服从对数正态分布。寿命数据经过Shapiro-Wilk 检验的P 值小于0.05，说明原假设不成立，寿命这组数据不服从对数正态分布。

由于检验出寿命数据不符合对数正态分布，因此使用实际工程中广泛应用的Weibull 分布模型，对前面的疲劳试验数据进行拟合，在S-N 曲线的基础上绘制出P-S-N 曲线。主要步骤如下：

Step1：根据疲劳试验数据对应力和寿命分别取对数，按照log（N）排序，计算累积失效率。

Step2：对疲劳试验数据进行Weibull 分布拟合，利用最小二乘法估计出Weibull 分布的形状参数和尺度参数。

Step3：经过逆变换得到失效率函数，从而得到可靠度函数。

Step4：绘制P-S-N 曲线，如图2 所示。

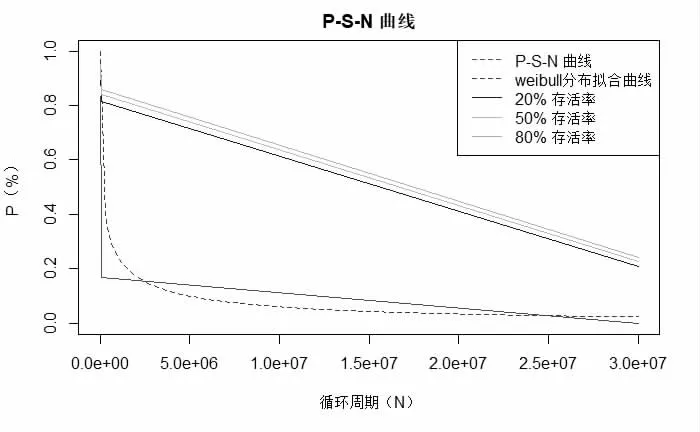
图2 GH4033 材料的P-S-N 曲线

利用R 软件计算出拟合的Weibull 分布形状参数m 为37.5，尺度参数 η为49735。此时，我们可以得到，航空发动机涡轮叶片在可靠度为0.5 时，它的循环周期为158045，即航空发动机涡轮叶片的平均寿命为158045 次循环。同时，对于航空发动机涡轮叶片，我们一般保证99.87%的可靠度，此时叶片的循环周期为15668。当航空发动机涡轮叶片循环周期达到15668以后，我们可以对叶片进行故障检修，对叶片发生故障的可能性进行评估，达到降低发动机出现故障的风险。

3 应力- 强度干涉模型下可靠性分析

大多数的合金结构服从对数正态分布，因此我们设航空发动机涡轮叶片的强度X～LN（），应力Y～LN（），X 与Y 相互独立，得到叶片的结构可靠度为

航空发动机涡轮叶片的安全系数一般1.2～1.5之间。

为了保证最大的疲劳强度，我们取安全系数K=1.5。

当航空发动机涡轮叶片的强度试验数据未知，而航空发动机涡轮叶片要保证99.87%以上的可靠度时，可以根据公式(7)和表6，估计出强度数据。由表2 我们可知，拉伸强度的真实值为880 MPa。表7 是疲劳强度在极大似然估计下的估计值。

表6 在安全系数K=1.5 的结构可靠度及可靠指标计算

表7 参数估计值与真实值的对比

4 结论

本文基于应力-寿命疲劳试验数据，绘制了S-N曲线和P-S-N 曲线，发现GH4033 型材料的航空发动机涡轮叶片是无限寿命设计，然后结合安全系数K，利用应力-强度干涉模型，对航空发动机涡轮叶片的疲劳寿命和可靠性进行分析。该模型可以进行故障风险评估以及优化涡轮叶片的巡检时间预测，减少发动机故障的可能性，延长航空发动机叶片的疲劳寿命。