Wordle答题情况的预测与分析

蔡忠哲，曾日威，林承铖，李韶伟

（台州学院电子与信息工程学院，浙江 临海 317000）

0 引言

Wordle 是《纽约时报》推出的一款“猜词”游戏，因具有趣味性和益智性，深受大众欢迎。Wordle 玩家可通过多次的“试错”得到线索，从而猜出“谜底”；而Wordle 依照“试错”的次数可以给玩家评分。本文利用该游戏的运作原理和单词的属性解决两个问题，以实现《纽约时报》可以预测未来某一天Wordle 游戏的答题情况，并对“谜底单词”进行难度分类。两个问题具体如下：

问题一：根据2023 年美国数学建模竞赛（MCM/ICM）赛题数据，建立合理的预测模型，预测2023 年3月1 日的答题情况，并研究单词属性对答题情况的影响。

问题二：建立“谜底”单词的难度分类模型，并说明分类结果的正确性。

1 模型建立与求解

1.1 ARIMA-LSTM预测模型

因赛题所提供的时序数据中含有线性和非线性成分，预测难度较大，所以我们选用了ARIMA-LSTM预测模型（自回归滑动平均取值和长短期记忆神经网络的组合模型：Autoregressive Integrated Moving Average，Long Short-Term Memory）［1-2］，以便精确地预测2023 年3 月1 日的答题结果。

1.建立ARIMA 模型（自回归滑动平均模型，Autoregressive Integrated Moving Average）。建立过程包括：数据的平稳性检验、差分化、确定参数、参数显著性检验、模型预测。

（1）平稳性检验。依据自相关函数ACF（Autocorrelation Function）和偏自相关函数PACF（Partial Autocorrelation Function）［3］的结果来量化数据的平稳性，定义自相关函数为

自相关数为

其中：ft为当天需要该次数完成游戏的人的比例数，为该段时间内需要该次数完成游戏的人所占比例数的平均值，E表示期望，k为滞后系数。

定义偏自相关函数为

根据原始数据描绘图形，如图1 所示。由图1 可直观看出，原始数据的平稳性不佳，需要对其进行差分处理。

图1 原始数据图形

（2）差分化。根据人们的数据处理经验，对数据差分的阶数不宜过高。本文对数据经过一阶差分处理，即可得到“平稳”的数据，因此确定差分阶数d= 1。

（3）确定参数。通过对自相关ACF 和偏自相关PACF 进行分析，确定ARIMA 模型的参数p和q，相关的数据图形如图2 所示。

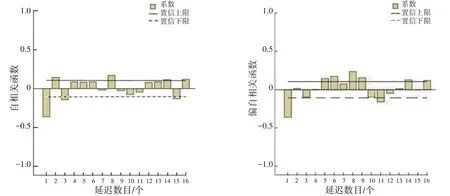
图2 自相关图与偏自相关图

从图2 中的自相关ACF 图可以看出，数据为3 阶拖尾；而从偏自相关PACF 图可以看出，数据为1阶拖尾。因此，可以确定p= 3,q= 1。这样，模型的3 个参数(p,d,q)已全部确定。

（4）参数显著性检验。通过残差检验来判断数据是否为白噪声序列，基于假设检验H1和H0，通过构建LB（Ljung-Box）统计量来分析，即

假设H1成立时，模型有效性显著；而假设H0成立时，残差序列存在线性关系，模型的显著性不足。通过实际的数据检验可得H1成立，模型有效性显著。

（5）ARIMA 模型预测。经过上述步骤，模型被确定下来，使用该模型可预测得到各类型人数的比例，即

其中：Yt-j为差分平稳序列；Zt-m表示随机误差；p为自回归系数；q为移动平均数。

经过模型预测，可得到从2022 年1 月1 日至2023 年3 月1 日的答题情况，如图3 所示。接着，可进一步得到2023 年3 月1 日的预测结果。

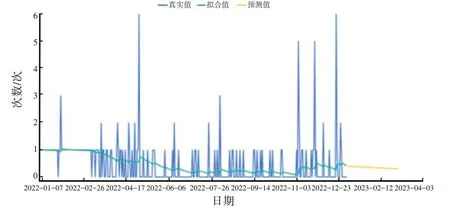
图3 2022 年1 月1 日到2023 年3 月1 日的预测结果

2.构建LSTM 模型（长短期记忆神经网络，Long Short-Term Memory）。建立过程包括：处理数据、参数设定、训练与输出。

（1）处理数据。将原始的序列数据做类似归一化处理，得到：

其中：yt1为处理后的数据，ytmax、ytmin分别为最大值、最小值。

（2）参数设定。对于LSTM 模型中的参数，包括训练窗口数、节点数、迭代训练数等，为保证预测的效果，选用修正线性激活函数ReLU（Rectified Linear Unit）［4］。

（3）训练与输出。输入答题人数进行训练，使用ARIMA 模型预测答题情况，经反向归一化后得出预测值。为保证预测的准确性，采用加权平均方法将两种结果结合起来，得到更为合理的预测值，如表1 所示。

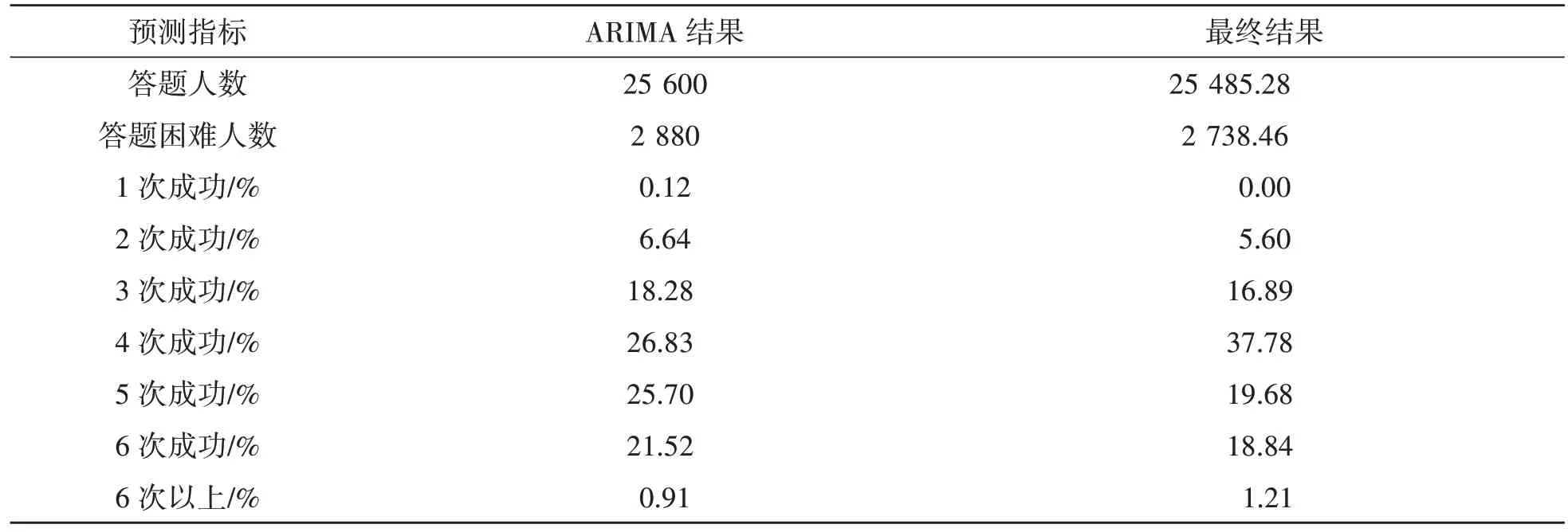
表1 预测结果

1.2 K-means聚类分析模型

K-means 聚类分析［5］可实现高效的分类，要依照难度对“单词”进行分类。首先，要确定每一个单词的“难度”。显然，体现单词难度的指标有很多，例如单词生僻程度、单词中重复字母出现的个数等，为避免人为赋值的主观性，这里采用所有人通过游戏所需不同次数的概率Pi来构建难度指标。

（1）指标选取。对一个单词来说，确定简单模式的人为V，困难模式的人为T，简单模式下不同次数通过游戏的人为（v1，v2，...，v7），困难模式下不同次数通过游戏的人为（t1，t2，...，t7）。那么，对该单词来说，第j次通过的概率为

但是，每个单词在困难模式和简单模式下耗费不同次数通过游戏的人数是未知的，因此上述公式无法直接求解。对公式进行放缩后得到：

经过变形，上述不等式的两边都是可求的，此时Pj可简化为取两数的平均值，即

由此下来，每个单词的难度指标已构建完成。根据选取的指标，计算每个单词各项难度指标值，得出题目所给单词的难度特征。

（2）原始数据标准化。建立原始数据与处理后数据的关系式：

其中：X为原始数据；x为处理后的数据。

将处理后的数据集分为4 类，在数据集中随机选取4 个中心点，坐标为

（3）计算距离。计算得到所有点与中心点的距离：

其中：Dm,i为第m个点到第i个中心点的距离；m为数据点个数；为第m个点第k项指标值。

（4）聚类分组。根据所有的点与各中心点的距离，把所有的点分配给距离其最近的点，形成一个小类群。

（5）中心点的计算。设置每个类群中心点的计算公式，即

其中：xj,i为该类群中第j个点第i项分量；M为该类群中点的个数。

（6）迭代。不断重复上述步骤，直到迭代收敛，所有的点被分为几个小类群，也得出了每个类群的中心点。对所给点进行聚类的结果如图4 所示。

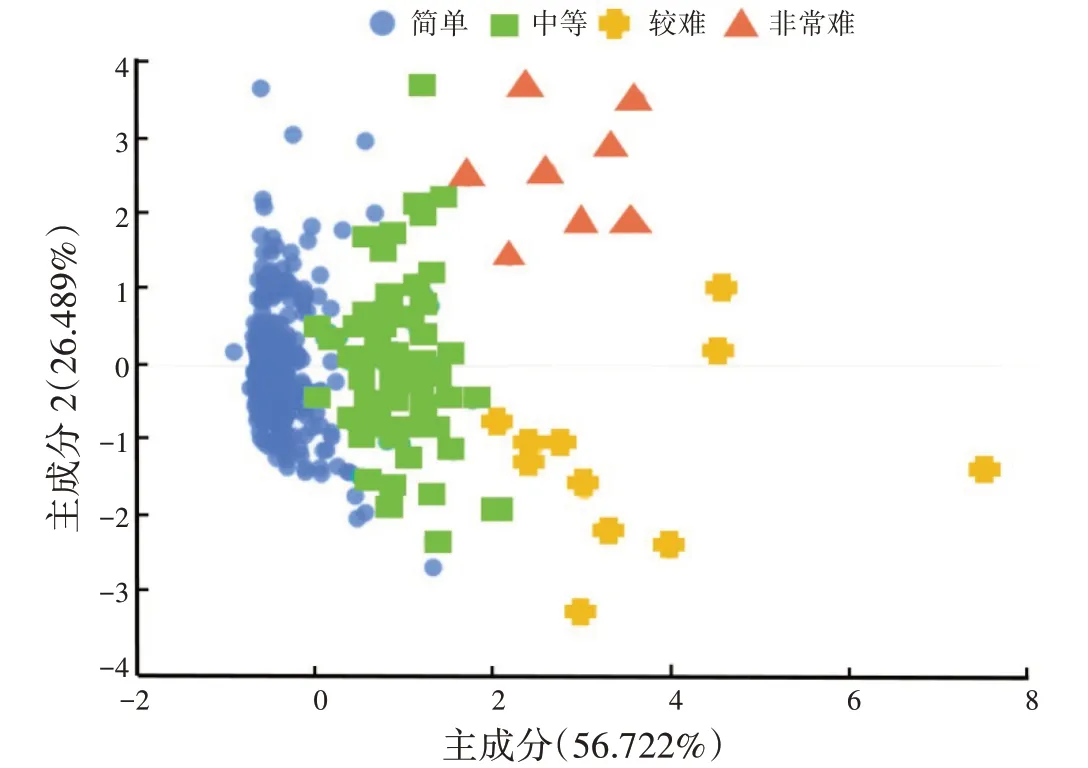
图4 聚类散点图

由图4 可知，聚类结果共分为4 类，各类占比分别为78.552%，16.156%，3.064%，2.228%；将4 类结果分别命名为简单、中等、较难、非常难。经验证，该分类结果与实际相符，数据可靠。

（7）轮廓系数计算。为了说明分类模型的聚类效果较好，引入衡量聚类效果优劣的轮廓系数，它是一个可以用来描述聚类后各个类别轮廓清晰程度的指标。

首先，定义内聚度，即求出一个点与所处类群内元素的紧密程度，公式为

其中，Dij为第i个点到第j个点的距离，内聚度越小说明结构越紧密。还需要在每一个类群中计算bi，计算方法同aj，但要取其最小值，即

接着，定义轮廓系数，公式为

轮廓系数的取值在-1～1 之间，轮廓系数越接近1，说明聚类效果越好；反之，效果越差。经过计算，分类结果轮廓系数为0.83，数值接近1，说明分类后轮廓清晰，效果较好。

（8）模型准确性验证。为了验证分类模型的准确性，即确定预测分类结果和实际分类结果的差异，引入用于显示预测情况与真实情况差异的混淆矩阵［6］。首先，根据分类结果构建4×4 的矩阵A(aij)。其中，aij表示实际属于第i类而被预测为第j类的个数。接着，定义几个重要的指标：TP(i)表示实际为第i类而被预测为第i类；FP(i)表示实际为其他类而被预测为第i类；TN(i)表示实际不是第i类，预测也不是第i类；FN(i)表示实际为第i类而被预测为其他类。最后，引入精度和正确率指标，计算公式分别为：

其中，M为样本总数。分别计算出4 类结果的TP(i)，FP(i)，TN(i)，FN(i)，如表2 所示。

表2 混淆矩阵的几个指标

按照式（17-18）分别计算出分类模型的精度和正确率，如表3 所示。由表3 可知，精度和正确率可以说明分类模型的效果，数值越高说明分类模型准确性越强。从表中正确率可以看出，本模型对简单和中等难度单词分类的准确性较高，对较难和非常难单词的分类准确性一般。由于较难和非常难的单词在所有单词中占比较低（<5.3%），所以分类结果不会对游戏造成负面影响。

表3 分类模型的准确性和精确度

2 结语

本文首先构建了ARIMA-LSTM 模型来预测Wordle 的答题情况。通过数据分析，确定模型的参数值，再综合两个模型的预测值，给出2023 年3 月1 日的预测结果。根据结果，3～6 次尝试的成功率占比总计达92.33%，说明绝大多数人需要通过3～6 次尝试才能完成比赛。其次构建了单词的“难度”指标并进行聚类分析。根据聚类结果，将所有单词分为简单、中等、较难、非常难4 类，其中简单类占比最高；同时成功利用混淆矩阵引申出的精度和正确率，衡量单词分类结果的准确性。结果表明：大多数被选为“谜底”的单词是较为简单的，这也比较符合实际。因为如果选择的单词很难，会大大削弱玩家的参与热情和积极性，不利于游戏推广。因此，Wordle 游戏可采用本文的模型确定备选谜底单词的“难度”，避免将难度太高的“单词”作为“谜底”。