基于AHP-Fuzzy法的地铁盾构施工风险评价

朱永祥,管红兵,闫秀芳

(滁州职业技术学院 建筑工程学院,安徽 滁州 239000)

一、引言

随着我国经济社会的发展,城市化建设水平也日新月异,但城市人口的剧增,同时也带来了繁重的交通拥堵问题,一些大城市开始建设城市轨道交通项目来解决这一问题[1]。在城市轨道交通项目中,地铁是较为常见的轨道交通类型。地铁具有运距大、效率高、准点率高以及载客量大的优点,但其建设难度却远超一般建设项目。

地铁的修建方法,有明挖法、盾构法等,其中盾构法是目前地铁建设中地下隧道修建的常见方法。盾构法是指利用大型盾构机械,完成掘进取土、隧道管环安装、同步注浆等工序,并循环交替前进,直至隧道贯通[2]。盾构法具有施工机械率高、施工效率高、对地面交通影响小的诸多优点,但施工风险高也不得不引起关注,近年来,在国内一些城市修建地铁的过程中,出现了诸如地面塌陷、周边建筑受损的风险问题,一些问题甚至导致了人员伤亡。

对盾构施工开展风险评价,是实施风险管理,并有效降低风险的基础。风险评价主要通过运用风险评价方法,对影响盾构施工安全的风险因素指标进行识别,再用这些指标对施工安全风险的影响程度进行评估,最终确定出盾构施工的风险安全等级,为采取相应的风险措施提供依据。国内在盾构施工风险识别、评价及预测方面的研究也已成为广大研究人员关注的重要领域。如王胜楠(2021年)通过综合采用专家调查、WBS、4M1E等方法,确定了具有一般通用性的盾构施工过程风险清单和盾构施工设备风险清单[3]。朱倩倩(2020年)在沉降风险预评价的基础上构建改进的PSO-RBF神经网络预测模型,通过沉降预警阈值的设定达到施工过程中对地面沉降量进行预警的目的[4]。赵雅云在(2017年)将可拓评价方法运用于地铁盾构施工的安全风险评价中,并结合工程案例予以验证[5]。赵珍妮(2021年)在模糊综合贝叶斯网络法的基础上对地铁盾构施工风险评价开展研究,取得了实际应用效果[6]。赵辉等(2021年)构建了基于PCA-Shapley值的地铁盾构施工风险灰色聚类评价模型,通过实际案例得到应用[7]。上述所提及的风险评价方法,应用过程相对复杂,且对专业知识的要求较高,相对而言,近年来被广泛应用到风险评价问题中的层次分析法及模糊数学评价法,以及兼容了层次分析法和模糊数学评价方法优点的AHP-Fuzzy,其应用过程相对简单,评价结果具备足够的准确性,能满足对风险评价问题的使用要求。

二、AHP-Fuzzy法概述

AHP-Fuzzy法即基于层次分析法的模糊数学综合评价方法,其中AHP为层次分析法的英文简写,Fuzzy则指模糊数学评价法。模糊数学评价法的基础为模糊数学,模糊数学的提出主要是基于客观世界存在许多不确定性现象,无法给出具体的定值描述和边界划分;而风险问题或风险现象,在对其评价风险程度或风险发生概率时,无法用具体的语言表达,而只能使用一些模糊性的语言表述,如表达风险程度时,用严重、轻微等语气用词,表达风险发生概率时,则使用可能、大概率等语气用词。其次,对应风险问题的形成,又直接或间接受到来自外界或自身多种因素的影响,存在多种性质不同、程度不同、发生概率也不同的风险源。因此,对应风险评价问题往往采用模糊数学评价方法。

决定风险问题评价等级的指标是指影响风险程度或风险发生概率的各种风险因素,这些因素对风险的形成有着不同的影响权重,权重代表了该指标在整体中的相对重要程度,因此,赋权也是评价方法中的核心问题之一,模糊数学评价法在对各种风险指标分析时,需要将各类风险指标按照隶属层级关系,划分指标层次,再对各层级指标赋予不同的权重,权重的确定除了可以通过专家主观判断法,更为客观的方法主要使用层次分析法。层次分析法(AHP)是美国运筹学家萨蒂于上世纪70年代初,为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法[8]。该方法将半定型、半定量的问题转化为定量计算,确保了指标赋权的客观性和准确性。

AHP-Fuzzy法将层次分析法和模糊数学评价法有机结合起来,利用AHP法,完成评价问题的层次划分以及各层次指标因素权重赋值;再利用Fuzzy模糊数学评价方法,通过构建模糊评价矩阵,计算出综合隶属度,定量确定出风险等级。

三、AHP-Fuzzy法在盾构施工风险评价问题的应用

本文所探究的盾构施工风险评价问题,具有模糊评价性质。从影响盾构施工的风险因素分析看,盾构施工的风险源较多,如施工资源要素的风险源、施工技术的风险源、施工管理的风险源、施工环境的风险源等,且这些风险源互相影响和干扰。对这些风险源的描述,也无法用具体的语言表达,而只能用模糊性的语言表达,因此,用AHP-Fuzzy法不失为一种用于解决盾构施工风险评价问题的方法。

(一)AHP-Fuzzy法的评价步骤[1]

1.构建风险评价因素集合

风险评价因素集合是将风险评价问题,按照风险形成的若干因素,分类形成不同类别因素所构成的数集。当风险评价问题较为复杂时,风险评价因素按风险属性在一级风险因素划分基础上,还可以进一步细化为若干层次的子因素数集。

即

U={U1,U2,…,Un}

其中U1还可进一步细分出相应的子因素集合。

Ui={ui1,ui2,…,uim}

这里定义U为一级风险评价因素集合,Ui为二级风险评价因素集合,uim为所识别出的具体因素。

2.计算出各层次风险因素的权重

在确定各层次风险因素权重时,采用层次分析法进行计算。

在应用层次分析法时,先构建完成各层次风险因素相互比较判断矩阵,其次,再利用根法求解出风险因素的权重,最后还需要进行一致性验证,确定权重的可用性,尽可能排除判断偏差。

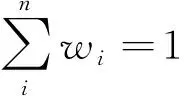
3.建立评价等级集

评价等级为专家针对各类风险因素对风险评价结果的影响程度,给出不同等级的评价语句,如对某一类风险因素,专家的评价等级可以用轻微、中等、较大、严重、重大等五个等次表示,当用数值量化后,则形成如下评价等级数集,即V={1,2,3,4,5},1对应轻微评价语句,依次类推。

4.构建风险因素的模糊判断矩阵

模糊判断矩阵R表达因素集U和评价集V之间的模糊关系,采用统计对某个风险因素持某等次评语的专家人数占专家总人数之比的数值表示模糊判断矩阵中的各个元素。

则风险因素的模糊判断矩阵可表示为

5.模糊综合评价,计算隶属度值

将风险因素的模糊判断矩阵与风险因素权重向量进行合成,再通过对矩阵计算分析,确定出各风险因素对应的风险等级。

B=WR=

|b1,b2,b3,…bm|

如果B中各组成元素总和不等于1,还需要对B进行归一化处理,形成归一化后的模糊综合评价矩阵B0=|b10,b20,b30,…bm0|。

对于多级因素构成的评价体系,需要进行多级模糊综合评价,并计算出综合隶属度。

(二)案例应用

下面通过某盾构施工安全风险评价问题,使用AHP-Fuzzy法开展评价分析,说明该评价方法的应用过程。

本案例以滁宁城际铁路二期工程为依托,该工程自滁州高铁站起至凤阳北路站,全长13.276千米,其中花博园站至市政府站区间沿线为该市主干道,周边建筑及地下管线较为密集,施工条件复杂,隐藏着较多的施工环境风险,该区间施工采用盾构法完成隧道开挖。虽然盾构法具有机械化程度高、对地面交通影响小、施工效率高的诸多优点,但由于暗挖作业,推进过程对地层扰动,不可避免诱发地层变形和周边建筑管线变位,从而可能造成一定的施工安全风险,甚至引发事故灾害。因此,为正确评价该盾构区间施工安全风险,根据评价结果采取必要的防控措施非常有必要。

1.施工风险识别并构建风险因素评价集合

首先根据所要开展的研究问题,采取征询专家意见、查阅相关案例资料等方式,将本项目施工安全风险评价问题,按照影响施工安全的风险因素的组成,构建递阶层次。影响施工安全的因素包括4M1E,即人的因素、机械设备因素、施工材料因素、施工技术因素以及施工环境因素五个方面。每类影响因素又可以细分为若干项子因素,最终构建出如下多层次评价指标体系。

其中人员、机械、材料、施工方法、施工环境构成了盾构施工风险评价问题的二级风险因素。每个二级风险因素之下又细分出若干个三级风险因素。以下用数学的方式构建出盾构施工风险评价因素集合。

U={U1,U2,…,Un}=

{人员,机械,材料,施工方法,施工环境}

人员={人员能力水平,人员职业素养,

人员身体状况,现场管理制度}

其他二级因素的细分,可参考人员风险因素的分解,这里限于篇幅,不再详细列出。

2.构建判断矩阵,完成各层次风险因素的权重计算

判断矩阵的构建,采用0～9标度法,通过向专家征询意见的方式,对风险评价指标进行两两对比,根据对比结果,赋予风险评价指标相应的分值,最后通过yaaha软件完成各指标权重辅助计算。限于篇幅,这里仅举例一级风险因素以及二级风险因素中人员风险的判断矩阵构建、各风险因素的计算过程和结果。

表1 一级风险因素判断矩阵表及权重计算结果

表2 二级风险因素(人员风险因素)判断矩阵表及权重计算结果

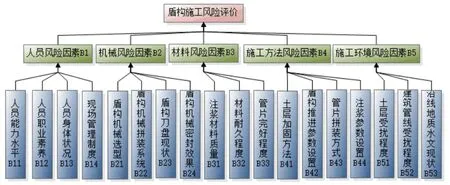
图1 案例工程盾构施工风险因素层次结构图

3.建立评价等级集,并构建各层次风险因素的模糊判断矩阵

采取征询专家意见的方法构建评语集,根据风险评价所需的专家学识、特长等条件,邀请了10名专家组建专家小组,这些专家包括盾构施工方的工程技术人员、从事盾构施工教学和研究的高校教师以及盾构施工监理方、项目建设单位方等专家,由他们对项目的风险情况进行评价。

经过专家的综合评价,认为本项目盾构施工的风险评价等级可以划分为五个级别,依次为无风险、较轻风险、中等风险、重大风险、极大风险。于是,形成了风险评价评语集如下:

评语集=(无风险、较轻风险、中等风险、重大风险、极大风险),用具体数值量化为V ={1,2,3,4,5}。其次可根据风险因素类别,按照风险评价等级,10名专家分别对这些风险因素进行不同等级评价,按照对同一因素持不同评价等级的专家人数构建模糊判断矩阵,并归一化处理后如下:

这里以人员风险因素为例,说明模糊判断矩阵的构建方法。

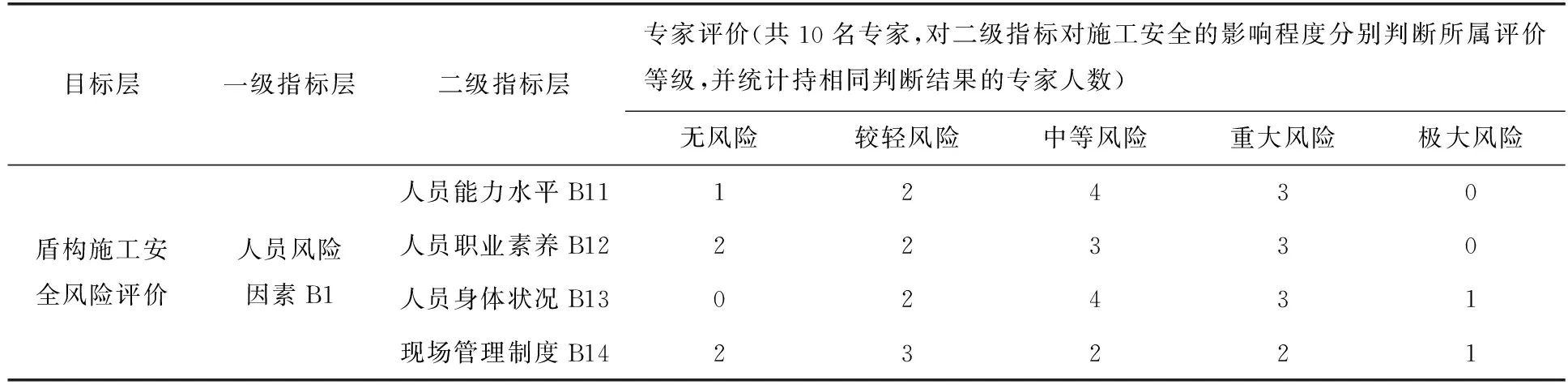
表3 人员风险因素专家评价情况表

将上面的专家打分情况,归一化处理形成模糊判断矩阵如下:

人员风险因素B1模糊判断矩阵

其他因素按照同样方法,形成相应的模糊判断矩阵。

4.模糊综合评价,计算隶属度值

首先进行二级风险因素评价隶属度计算:

人员风险因素B1评价隶属度

S1=W·R=

其他二级风险因素,按照同样的方法依次完成评价隶属度计算。

在二级评价基础上,进行一级评价如下

S=

已知一级指标层中各风险因素的权重集向量如下:

W=

于是,一级模糊评价矩阵构建如下

U=W·S=

在此基础上,一级风险因素的评价得分计算如下:

F=U/·VT=

在对二级风险因素评价时,这里只给出人员风险因素B1的评价得分计算过程,其他二级风险因素可按此方法计算,这里不再赘述。

F1=S1·VT=

综上,该盾构施工风险评价结果见下表4。

表4 盾构施工风险评价结果

四、结论

AHP-Fuzzy法在风险问题评价方面有较好的应用。研究依托某地铁工程盾构施工实例,应用该方法完成盾构施工风险问题的评价分析,在确定风险因素指标权重值时,则采用层次分析法完成其不同风险指标的权重计算。

研究的最终结论表明:对盾构施工风险评价结果影响的五类一级指标风险等级均为中等,在此基础上,对盾构施工风险评价总体结果也为中等,表明了各类现状风险因素均具有可控性。在实际施工中,应加强对风险因素的监测,及时发现风险异常现象并予以控制,从而保障该盾构施工预期目标实现。