基于高考题探究高中数学解题技巧教学——以数列题为例

杨红利

(江苏省如皋市长江高级中学,江苏 如皋 226500)

数列是指按照一定规律排列的一系列数的集合,是高中阶段的一个重要内容,同时也是高考必考内容之一.该类题在解答题、选择题和填空题均会有所呈现[1].主要考查以下几个方面:(1)考查等差数列和等比数列的基础知识、数列的单调性及周期性等;(2)考查通过已知条件求数列的通项公式;(3)考查在解决数列的基本问题之后,考查数列求和方法,在此基础上,进一步考查“裂项相消法”“错位相减法”等方法.在求和之后,可能会与不等式、函数、最值等问题进行综合.注意当与不等式结合时,“放缩”思想及方法尤为重要;(4)考查“新数列”是等差或等比数列的证明方法,并求出通项公式[2].

1 求数列的通项公式

求数列通项公式主要以考查由递推公式求通项公式,或已知前n项和求通项,或已知前n项和与第n项的关系式求通项为重点,特别是数列前n项和Sn与an关系的应用.该类题难度中等,常常出现在选择题、填空题以及解答题的第(1)小问中.

1.1 公式法

若能够根据题目中的已知信息,推出数列{an}是一个等差或者等比数列,则可以根据通项公式an=a1+(n-1)d或an=a1qn-1进行求解.

例1(2019全国1理9)Sn是等差数列{an}的前n项和.已知S4=0,a5=5,则( ).

A．a>0,b>0 B．a>0,b>0

C．a>0,b>0 D．a>0,b>0,

解析由题意可知,{an}是一个等差数列,则可以根据公式法进行求解.设等差数列{an}的公差为a>0,b>0,由a>0,b>0,得a>0,b>0,解得a>0,b>0,所以a>0,b>0,故答案为A.

1.2 Sn与an的关系式法

若已知数列{an} 的前n项和Sn与通项an的关系式,求an时,可以运用该方法求解.做题步骤为由Sn与an的关系式,类比出Sn-1与an-1的关系式,然后两式作差.要注意分n=1和n≥2两种情况进行讨论,一定要检验n=1是否也适合an.

1.3 累加法

当数列{an}中有an-an-1=f(n),即第n项与第n-1项的差是个有“规律”的数时,就可以用这种方法.解题步骤为首先写出所有项式子,而后等式的左右两边进行相加,最终运算求出通项公式.

例3已知a1=0,an+1=an+2(n-1),求通项an.

解析∵an+1-an=2n-1

∴a2-a1=1,a3-a2=3 ,a4-a3=5…

an-an-1=2n-3 (n≥2)

以上各式相加得an-a1=1+3+5+7+…+(2n-3)=(n-1)2(n≥2)

又a1=0,所以an=(n-1)2(n≥2),而a1=0也适合上式,

∴an=(n-1)2(n∈N*)

2 数列求和

高考数列求和部分重点考查裂项相消法和错位相减法,多为解答题第二问,难度为中档.

2.1 利用常用求和公式求和

该方法比较简单,根据等比数列或者等差数列的求和公式进行运算即可.

解析设等差数列Sn的公差为Sn,则由Sn,Sn可得,Sn,Sn.

2.2 裂项法求和

裂项相消法就是将数列{an}的每一项进行分解,使相加后项与项之间能够相互抵消,但在抵消的过程中,有的是依次项抵消,有的则是间隔项抵消.其可以细分为以下几种:

表1 裂项相消常用公式

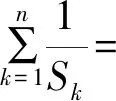
2.3 错位相减法求和

如果数列{an}是等差数列,{bn}是等比数列,求数列{anbn}的前n项和时,常采用错位相减法.做法为在等式两边同时乘以等比数列的公比,然后将Sn和qSn两式相减.

例6(2020年高考数学课标Ⅲ卷理科)设数列{an}满足a1=3,an+1=3an-4n．(1)计算a2,a3,猜想{an}的通项公式并加以证明;(2)求数列{2nan}的前n项和Sn．

解析(1)由题意可得a2=3a1-4=9-4=5,a3=3a2-8=15-8=7,由数列{an}的前三项可猜想数列{an}是以3为首项,2为公差的等差数列,即an=2n+1,证明如下:当n=1时,a1=3成立;假设n=k时,ak=2k+1成立．那么n=k+1时,ak+1=3ak-4k=3(2k+1)-4k=2k+3=2(k+1)+1也成立．则对任意的n∈N*,都有an=2n+1成立;

(2)由(1)可知,an·2n=(2n+1)·2n

Sn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n,①

2Sn=3×22+5×23+7×24+…+(2n-1)·2n+(2n+1)·2n+1,②

2.4 分组法求和

就是将数列的项分成几项,将这几项分别求和,然后再合并,从而得到该数列的和.例如当一个数列可写成cn=an±bn的形式,而数列{an},{bn}其中一个是等差数列,另一个是等比数列时,那么可用分组求和法.另外,如果一个数列可写成cn={an,n为奇数;bn,n为偶数}的形式,也可以使用该方法.

例7(2016年全国II)Sn为等差数列{an}的前n项和,且a1=1,S7=28．记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1．

(1)求b1,b11,b101;

(2)求数列{bn}的前1 000项和．

(2)记{bn}的前n项和为Tn,则T1 000=b1+b2+…+b1 000=[lga1]+[lga2]+…+[lga1 000]．

当0≤lgan<1时,n=1,2,…,9;

当1≤lgan<2时,n=10,11,…,99;

当2≤lgan<3时,n=100,101,…,999;

当lgan=3时,n=1 000．

∴T1 000=0×9+1×90+2×900+3×1=1 893.

3 数列与二次函数

通项公式、前n项和公式都是关于正整数的函数,要善于从函数的观点认识和理解数列问题.在高考中,经常将函数与数列的最值以及数列的取值范围结合起来进行考查.在求解时,考生很容易忽视n为正整数的特点,或即使考虑了n为正整数,但对于n取何值时,能够取到最值求解出错.在关于正整数n的二次函数中其取最值的点要根据正整数距离二次函数的对称轴远近而定.

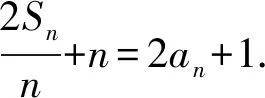
(1)证明:{an}是等差数列;

(2)若a4,a7,a9成等比数列,求Sn的最小值．

得2Sn+n2=2ann+n,①

所以2Sn+1+(n+1)2=2an+1(n+1)+(n+1),②

②-①,得2an+1+2n+1=2an+1(n+1)-2ann+1,化简得an+1-an=1,所以数列{an}是公差为1的等差数列．

通过对高考数列题的深入研究和探讨,我们可以发现数列题的解题技巧和方法并不是固定的,而是需要根据题目的具体情况来灵活运用.因此,在教学中,教师应该注重培养学生的数学思维能力和解题策略,帮助学生理解数列的概念和性质,并掌握数列题的常用解题方法.同时,学生也应该注重平时的练习和积累,不断巩固和提高自身的解题能力.