基于整数规划模型的生产订单分配及运输的最优策略＊

黄朝阳，蔺艳阳，李诺琳，吴兴艳，韩锋，张景胜

（北京联合大学，北京 100020）

0 引言

提高经济效益是企业现代化管理的根本任务，成本控制在使企业获得更高的经济效益上有着举足轻重的作用。只有努力加强成本管理、优化资源配置、提高产品品质等，企业才能获得长久发展的动力。随着企业间的竞争越来越激烈，许多企业通过控制生产成本、物流运输成本、储存成本等，全方面控制成本，提升企业竞争力。想要获得长期的效益，不能一味地降低人工成本与原材料成本，而是要从战略的高度实施成本控制，在现有“产供销”方案的基础上进行创新和优化，合理提高生产力，调整订单分配策略、物流运输战略、存储战略，使企业更快地适应新市场［1］。数学建模仿真所使用的Matlab、Simulink、SystemView 等软件计算仿真功能强大，应用范围广泛，能完成数据和数值分析等工作，可以极大地提高教师使用软件的灵活度和熟练度［2］，常被用作处理涉及大量数据的企业生产规划与运输管理问题。文章研究分析生产优化和物流运输，探索使综合成本最小的解决方案。

1 问题背景及简述

在首届北京市属高校数学建模联盟赛中，A题旨在引导大学生通过数据分析与建立数学模型解决综合成本最小化的成本控制问题。A 题题干如下：某集生产端、供应链公司和销售端一体的食品集团，随着该企业不断扩展业务范围，近期的战略重点开始转向预制菜业务。随着预制菜业务的迅速增长，沿用以往经验进行的管理，有可能导致供大于求，造成资源浪费；有可能导致供不应求，丢失应有的市场份额。该企业为使预制菜业务更快地打入市场，实现盈利，需要结合生产能力和市场变化平衡供需矛盾，做到既不浪费，又可满足市场需求，同时使公司效益最大化，则需要根据各产品的销量高低、毛利率高低、市场最新竞品情况等因素综合定制各产品的需求量，确定各产品最终的要货量、订单分配以及物流运输方案。现要将15 种产品分别由5 个不同的工厂运往分布在不同城市的分仓中备货，以供销售端需求，其中供应链公司将会在第1 周收集销售端第4 周、第5周的需求量并将订单分配给5 个工厂，5 个工厂则需要根据要货量在接下来的两周中，即各厂总工作时间均不大于240 h 的情况下，生产出足够的产品并运往各分仓。其中，各工厂生产工序中的设备具有并行性和可替代性，不同产品的产能存在相互制约的情况，并且对于成本问题，供应链公司要平衡需求与供应之间的矛盾，以最小综合成本（生产成本+物流运输成本）满足销售端需求的问题，即根据需求量和各公司产能情况，结合综合成本，在最大化满足需求量的前提下，将订单合理地分配给5 个工厂。附件2 阐明各个工厂产能及其生产各个产品所需成本。附件3主要提供的数据为各厂到各分仓不同箱规产品的单盒平均物流运输成本。附件4提供各产品运输所要求的箱规及近2周在各仓的要货量。由于设备产能存在瓶颈，当销售端需求不能被满足时，需要进行合理的调减测算，从而有效提升销供产各方的沟通及决策效率，确定各产品的最终要货量和订单分配方案。并针对附件4中数据，分析并解决以下问题。

问题一：现根据附件2 的工厂产能情况，在不考虑成本的前提下，建立模型分析5 个工厂能否在2 周内完成附件4中要货量的需求。

问题二：基于问题一可能出现的2 种不同结果，分别进行解决。若问题一中可以满足需求，则需要在满足综合成本最小的情况下将订单量合理分配给5个工厂；若问题一的结论是不能满足需求，则需将要货量适当等比例减小，以刚好达到产能能够满足要货需求且剩余10%的要货量的要求，在此基础上，同时满足综合成本最小，并且订制分配方案。

企业采购、生产、仓管、销售等各个环节的数字化和智能化可以有效地提升企业管理效率和效益，帮助企业降本增效，提高企业可持续竞争力［3］。针对企业生产优化和物流运输使综合成本最小化的问题，根据其“产供销”一体化管理，结合满足要货量需求，生产工艺和工时及运输要求的约束条件，建立以三维数据为基础的整数规划模型，利用Lingo 编程进行求解，可以同时得到最佳的订单分配方案和物流运输方案，使企业的综合成本最小化，获得最大的经济效益。依据题目建立的模型，系统地分析、规划供应和转运的最优方案，在企业实际采购方面具有一定的参考价值。模型中分析问题、解决问题的方法与思想针对其他模型也可以使用。因此，可以将本生产成本分析模型推广运用到其他企业［4］。

2 模型假设和符合说明

2.1 模型假设

本文模型假设如下：①生产工序仅考虑3个瓶颈工序，忽略其他工序；②在生产周期的2 周时间内设备正常运行；③忽略产品在运输途中的损耗；④假设运输量和要货量相等；⑤不考虑同一产品在不同设备之间转换的时间。

2.2 符号说明

基于整数规划模型的相关符号说明见表1。

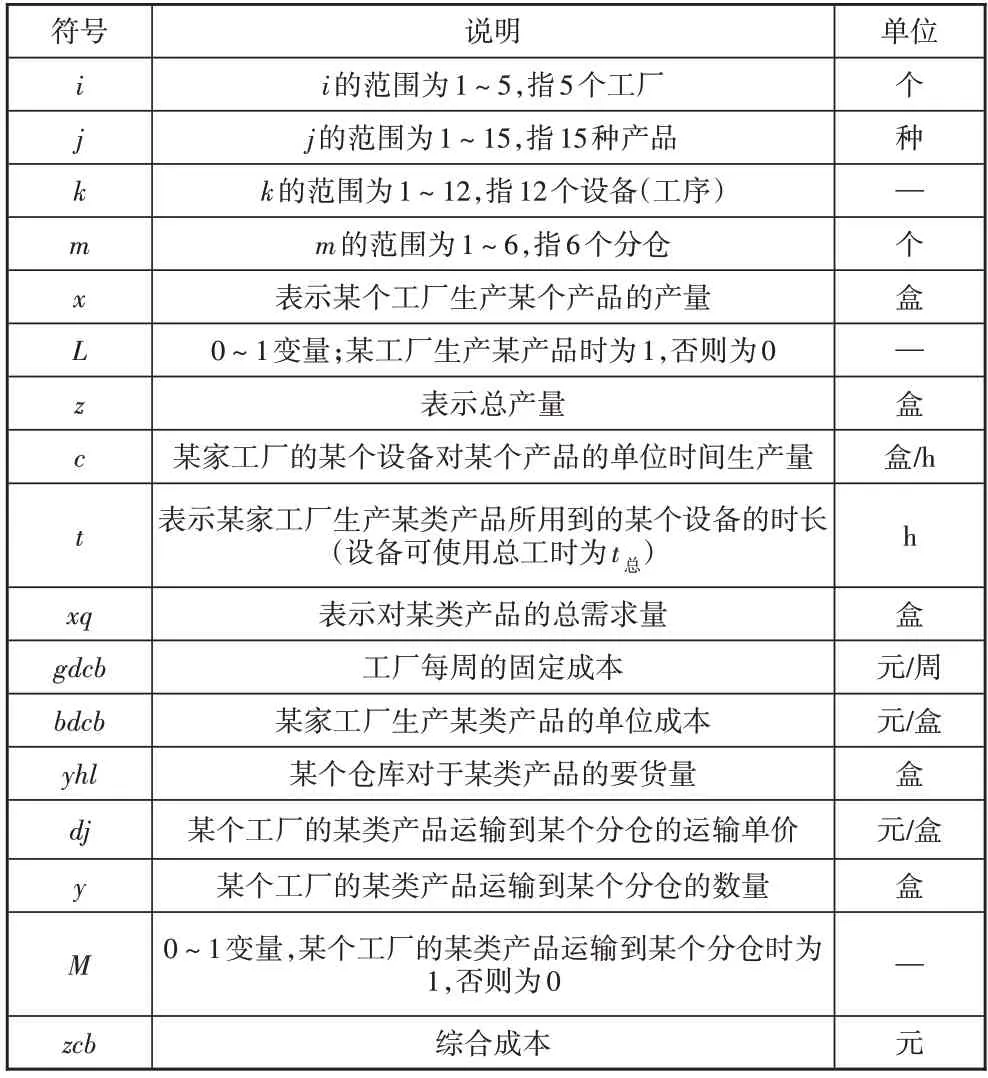
表1 基于整数规划模型的相关符号说明

3 问题分析

在问题一中，5 个工厂能否在2 周内完成要货量的需求时，要先考虑并分析产品加工的工作流程，根据附件中“热加工工序上，当一个产品在几类设备都有产能数据时，表示这个产品的工艺要求用这几类设备按一定顺序共同完成热加工”可知，热加工工序下6 种设备相当于串联关系。同理，根据附件中提出的“在内包装和速冻工序上，当一个产品在几类设备都有产能数据时，表示这几类设备具备可替换性，这个产品可以用这几类设备中的任何一类完成该工序”，故可将内包装工序中的4 种设备和速冻工序中的2 种设备分别视为并联关系，详细的生产顺序如下：整体流程（如图1所示）—产品8生产流程（如图2所示）—产品4 生产流程（如图3所示）。由背景信息可知，一种设备在单位时间内只能生产一种产品，但不同种设备可以在同一时间内生产不同产品，结合附件中所给的单位时间内每种设备的最大产能数据，只要在限制条件下生产量满足需求量即可，故该问题的解决方案为在先不考虑成本的情况下，假设每一种产品的5 个工厂生产总量超过该产品的总需求量，以每一类设备生产所有产品所用总时间不能超过2 周的总工时240 h，每个工厂的每一种产品都要经过不可替代的部分热加工工序，每个工厂的每一种产品都要经过可替代的内包装工序，每个工厂的每一种产品都要经过可替代的速冻工序作为限制条件，以5 个工厂的最大总产量为目标，建立整数规划模型，编写Lingo［5］程序进行求解。

图1 整体流程图

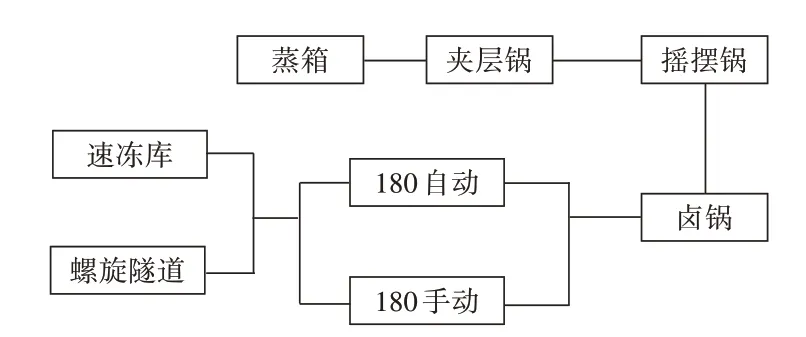
图2 产品8生产流程图

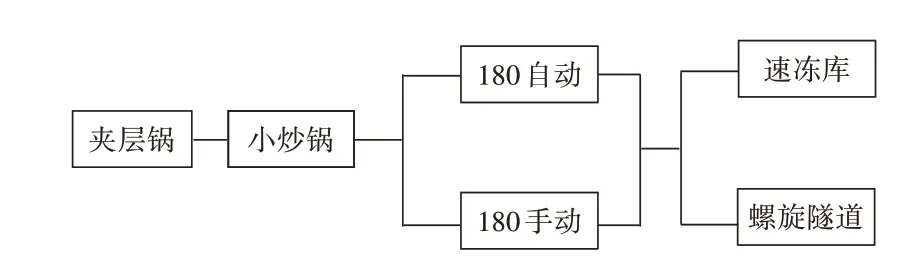
图3 产品4生产流程图

关于问题二，已于问题一中得知其在规定时间内生产量可以满足要货量，因此需要同时考虑生产成本（包含固定成本和变动成本）与物流运输成本。在满足综合成本最小的前提下，根据需求量同时得出5 家工厂的生产规划及运输到6 间仓库的物流运输方案［6］。层次分析法是一种计算简便且适合于多目标、多准则的系统评价方法，有许多其他方法不可比拟的优点。为有效解决生产企业的生产与运输问题，可以将这种分析方法的关键步骤与仓库选择决策问题相联系，用于生产企业的仓库选择决策上，以建立仓库评价的递阶层次结构，构建合适的层次结构模型［7］。根据综合成本最小原则，由于其固定成本不变，故只需考虑变动成本及物流运输成本，使该2项成本之和最小即可。保留问题一的限制条件，如某个工厂的各个设备生产15 种产品所花费时间ti，j，k之和均不能超过240 h。在此基础上，再添加5家工厂所生产的某类产品实际运输至某间仓库的总数量满足该仓库对该类产品的需求，同时5家工厂所生产的某类产品总和应满足实际运送至6间仓库的数量，即生产量大于/等于实际运输量，大于/等于要货量等限制条件，同时建立以二维数据和三维数据为基础的整数规划模型，使用Lingo 编写程序进行求解，得到最优的订单分配策略和最佳物流运输方案。

4 模型的建立与求解

4.1 问题一模型的建立与求解

4.1.1 模型的建立

在问题一中，先不计利润，只考虑满足要货需求，以5个工厂的最大总产量为目标，即

约束条件包括以下方面：

每一种产品的生产总量必须超过该产品的总需求量，即

每一个设备下所有产品加工所用总时间不能超过2周的总工时240 h，即

每个工厂的每一种产品都要经过不可替代的部分热加工工序，热加工工序所需每个设备的加工量都必须大于该工厂生产该类产品的产量，即

每个工厂的每一种产品都要经过可替代的内包装工序，只要可替代工序设备的总加工量都必须大于该工厂生产该类产品的产量，即可满足要求，即

同理，每个工厂的每一种产品都要经过可替代的速冻工序，速冻工序所需设备总加工量都必须大于该工厂生产该类产品的产量，即可满足要求，即

此外，由于现实生产问题存在生产数量必须达到一定值的要求才能生产，故在建立模型时运用0～1规划进行约束，经过对所给数据进行分析，可知某工厂生产某产品时，其最小生产量应不少于8 000件，为方便编程，对生产量的上限进行约束，需要取一个最大生产量达不到的值，该处取值为999 999 999，则该约束条件为

此外，所有变量只能取非负整数。因此，建立如下整数规划模型。

目标函数：

约束条件：

所有变量都取非负整数。

4.1.2 问题一模型的求解

为方便编程，在算法上做以下处理：将内包装工序和速冻工序中设备不生产某类产品时，单位时间产能空缺的位置补充为0，表示该设备下该产品的产量为0；热加工工序中的设备不生产某类产品时，相当于该类设备不启动，也就不用消耗工时，单位时间产能空缺的位置补充一个很大的数，假设该加工能力很大，消耗工时就会很少，程序中补充为999 999 999。

编写Lingo程序［5］，主要运行结果见表2。

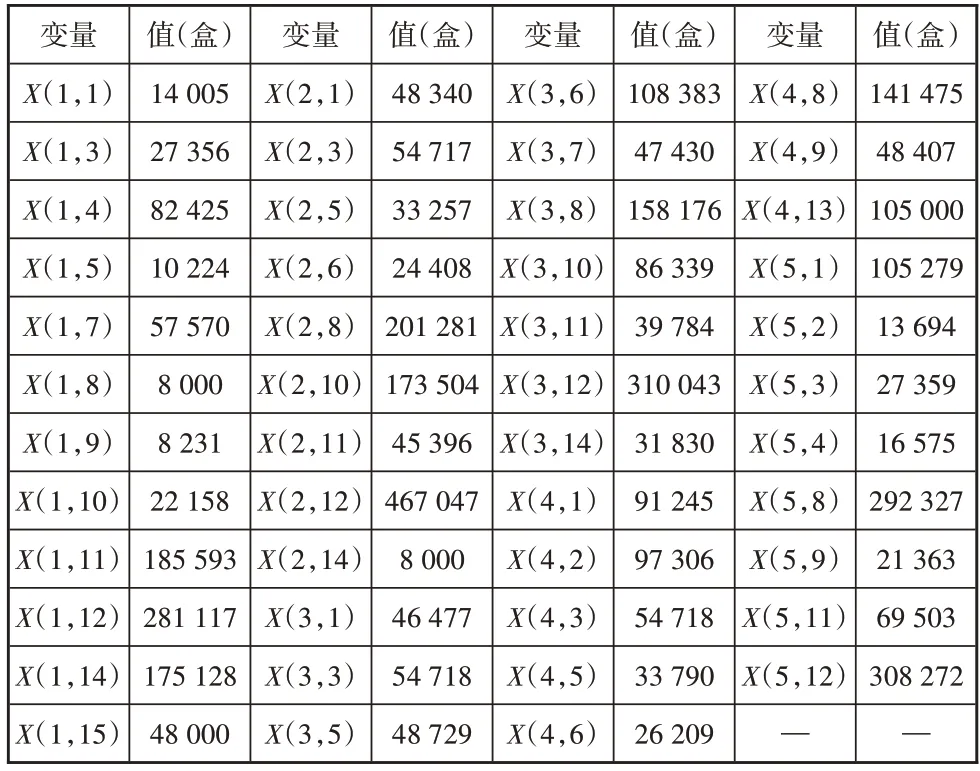
表2 各工厂能生产各类产品的数量

各分仓总要货量总计为180多万件，通过建模运算后，得到在规定时间内满足对各产品需求量的情况下，最大产量可以达到435 多万件，远远大于总要货量，其中每个工厂在规定时间内生产的各产品数量（见表2），如X（1，3）=27 356，表示在第一家工厂生产第三类产品的量为27 356 件，其余以此类推。综上，5 个工厂能在规定时间内可以满足总要货量需求。

4.2 问题二模型的建立与求解

4.2.1 问题二模型的建立

通过解决问题一可知，企业能完成要货量需求，因此第二问研究如何分配生产订单及合理制定物流运输方案，使综合成本最小化。

综合成本=生产成本+物流运输成本，全资工厂的生产成本=变动成本+固定成本，委外工厂的生产成本为各产品生产量×单件采购成本的和，即生产成本为

物流运输成本为运输量与单位运价的乘积之和，单盒物流运输成本主要与产品的包装规格和运输路程有关，即物流成本为

使目标最小化，即

约束条件要保留问题一中的所有约束，再通过物流运输的量保证各分仓的每一种产品均达到要货量要求，即

此外，由于现实运输中对运输的数量也有一定的要求，故在建立模型时同样运用0～1 规划对运输量进行约束，综合运输车辆的最大容量、各仓库的实际需求量及各工厂的生产量，结合运输费用应尽量减小的原则，得出某工厂运往某分厂的某产品时，单类产品最小运输量应不少于1 500 件，为方便编程，对运输量的上限进行约束，需要取一个最大运输量达不到的值，该处取值为999 999 999，则该约束条件为

因此建立线性规划模型如下［5］。

目标函数：

约束条件：

所有变量都是非负整数。

4.2.2 问题二模型的求解

为方便编程，在算法上做了以下处理：内包装工序和速冻工序中的设备不生产某类产品时，单位时间产能空缺的位置补充为0，表示该设备下该产品的产量为0；热加工工序中设备不生产某类产品时，相当于该类设备不启动，也就不用消耗工时，单位时间产能空缺的位置补充一个很大的数，假设该加工能力很大，消耗工时就会很少，程序中补充为999 999 999。编写Lingo程序，程序运行主要结果见表3和表4。

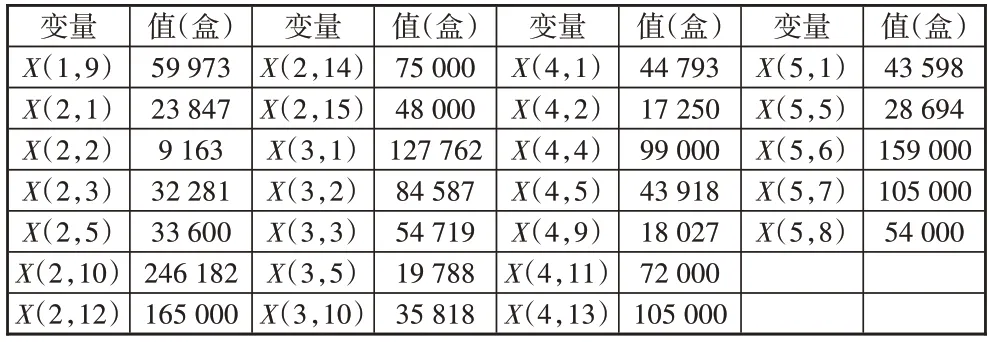
表3 各工厂生产各类产品的数量

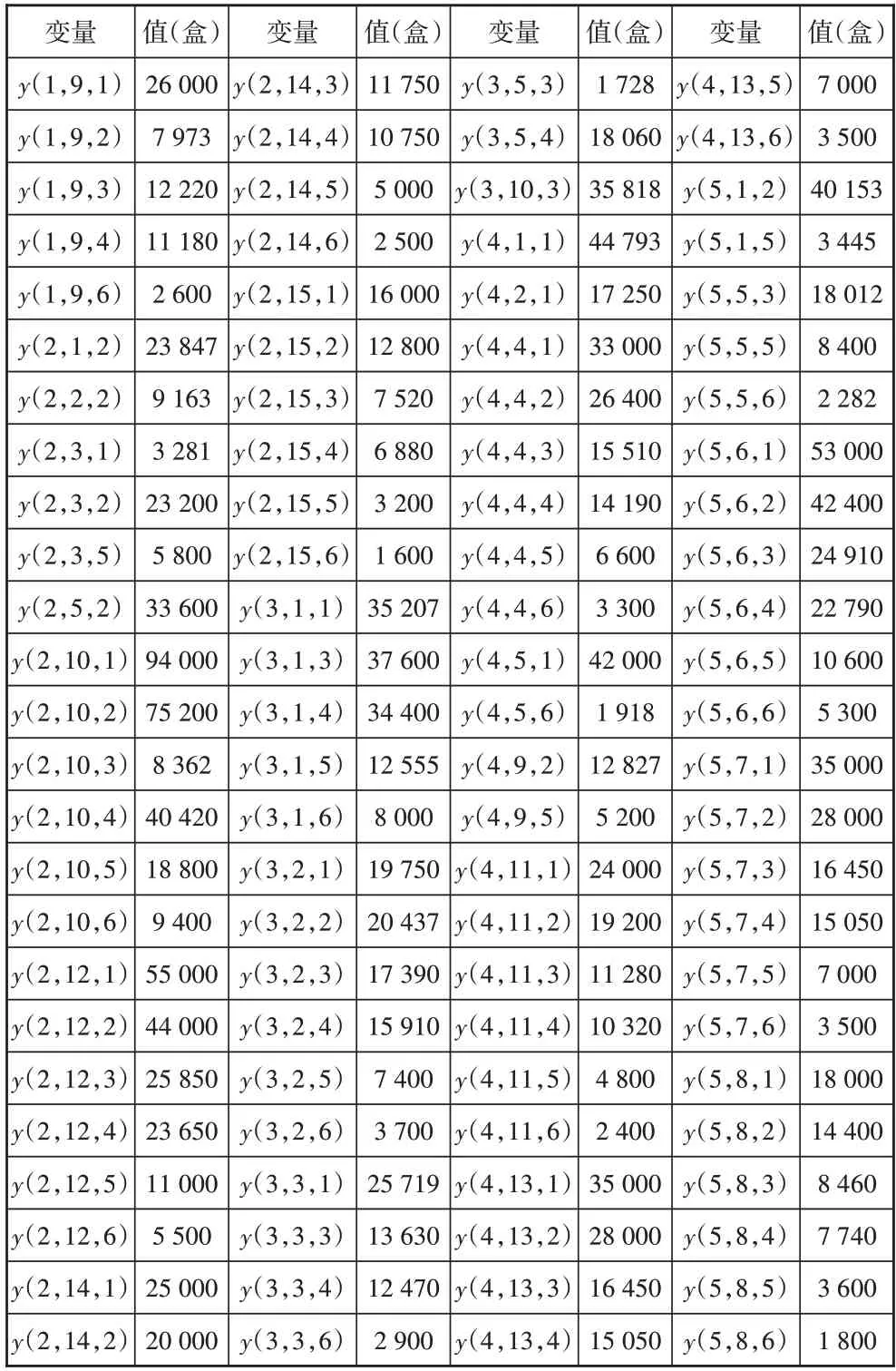
表4 各工厂生产的各类产品运输到各个分仓的数量

Global optimal solution found.

Objective value：0.394 907 8E+08

Total solver iterations：95 917

表3、表4 给出在综合成本最小情况下的订单分配策略和物流运输方案。例如，x（1，9）表示第1 家工厂生产第九类产品59 973件，y（1，9，2）表示第1家工厂运往第2 号分仓的第九类产品为7 973 件。按表2、表3所示结果进行生产和运输，即为综合成本最小的最优方案。

4.2.3 敏感性分析

敏感性分析用来评估输入变量变化引起的最优值的变化百分比。当输入变量变化时，不必重新解题就可以得到最优解的变化［8］。建立该模型的主要目标是实现企业经济效益最大化，即探究各种因素对综合成本的影响的敏感性。对单位成本bdcb、运输单价dj、单位时间生产量c和总工时t总4个重要因素，上下变化幅度为1%～2%，对应的综合成本的变化百分比如图4所示。

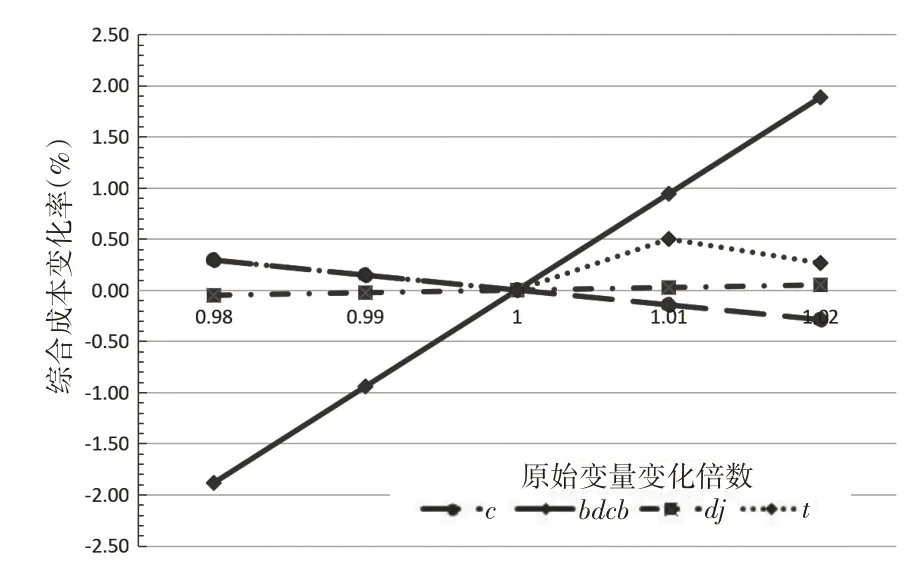
图4 变量敏感性分析

由图4 可知，综合成本zcb对于运输单价dj、单位时间生产量、总工时t总的灵敏度低，因此综合成本zcb相对于运输单价dj、单位时间生产量、总工时t总的稳定性好。综合成本zcb随单位成变化的百分比数值相当，综合成本zcb对于单位成本bdcb的敏感性不强，故综合成本zcb相对于单位成本bdcb的稳定性也较好。

5 模型评价

5.1 模型的优点

模型有以下优点：一是类比物理学中的串并联电路，形象理解不同的加工工序的本质区别；二是比较全面地分析问题，得到针对不同问题的整数规划模型；三是合理参考运输模型等典型模型；四是编写Lingo程序时，对于无需经过的工序，将其生产能力赋一个极大的值，以方便编程，节省软件运行时间，方便、高效地求解规划问题。

5.2 模型的缺点

模型有以下缺点：一是忽略产品在各个工序间转换的时间，得出的最大产能会高于实际最大产能；二是只考虑了3 个瓶颈程序，现实中的限制条件会更多。

6 模型推广与展望

6.1 模型推广

基于对此问题的理解与分析，问题一的模型还可以运用到各个厂家评估自己生产产品的产量能否在规定时间内满足客户的需求，如汽车、制药等行业。问题二的模型还可以应用于快递运输行业，即商家根据客户购买的物品从厂家那里购买之后用哪一种快递运送给客户的总成本最小。并且，可以解决网上超市一地多仓的订单分配与物流的配送问题。

6.2 模型展望

由于题目中给的单位运输价是盒/元，故建立的模型是按盒运送的，实际运输货物时是按箱运送的，不太符合实际运输情况，但是可以根据不同企业具体运输情况替换变量，进一步化为箱数进行运输，让箱数乘以容量恰好刚刚满足仓库需求量，此时计算运输费用，能更好地优化模型，得到更准确的综合成本。

7 结论

为使该企业获得最大的利润，本文依据集团产供销一体化的经营管理模式，基于满足要货量需求的基础，进一步详细研究了生产端、供应链公司及销售端中生产成本与物流运输问题，同时结合生产工艺和工时及运输要求的约束条件，建立以三维数据为基础的整数规划模型，从而确定了最佳的订单分配方案和物流运输方案，为其他相同或相似经营模式的公司提供有价值的参考模型，提高其决策效率和经济效益。