考虑信号传递路径的行星齿轮传动太阳轮裂纹故障响应分析

姚 俊，章翔峰，周建星，谢高敏，王烨锋，解开泰

（新疆大学智能制造现代产业学院，新疆 乌鲁木齐 830047）

引言

行星齿轮传动系统具有安全性高、体积小、噪声低、承载能力强等优点，在船舶、航空、风力发电等领域应用广泛［1］。然而，行星齿轮传动系统结构复杂，工作环境恶劣，导致设备故障几率大大增加，其中故障信号的采集受路径传递的影响，对故障早期诊断与预警造成极大干扰。因此，研究考虑信号传递路径的行星齿轮传动故障响应分析对系统故障诊断、预测，以及安全性评估具有重要意义。

国内外学者对行星齿轮传动系统故障响应分析已进行了大量研究。在振动响应求解方面，贺朝霞等［2］引入了时变的啮合刚度、综合啮合误差激励，建立时变的、多自由度耦合行星齿轮传动系统动力学模型，求解行星齿轮传动系统动态响应。黄奕宏等［3］推导了行星齿轮传动系统振动信号数学模型，分析了啮合频率周围调制边带产生的原因。许华超等［4］基于齿轮系统动力学推导出行星齿轮传动系统的平移-扭转耦合非线性振动微分方程，提出一种利用正弦激振扫频模拟行星齿轮传动系统内激励，并通过求解传动系统振动微分方程得到其响应的方法，从而量化评价各激励对系统振动响应的影响程度。在裂纹故障的产生方面，张俊等［5］基于势能法建立含齿根裂纹损伤的齿轮副啮合刚度与传动误差计算模型，求解行星传动系统的振动响应，揭示行星齿轮箱齿根早期裂纹损伤的故障机理。Han 等［6］分析了环齿轮裂纹故障对外啮合齿轮副之间动载荷的分配影响；Yang 等［7］考虑了齿裂纹张开状态对直齿圆柱齿轮副啮合刚度和动态响应的影响，证明了齿圈裂纹故障很少影响外啮合齿轮副之间的动态载荷分配。Zhang 等［8］分别采用集中质量模型和有限元模型对两级行星齿轮传动动态特性进行对比分析，研究了耦合-扭转刚度、耦合-平动刚度对系统振动模式的影响。Wan 等［9］计算了含裂纹损伤齿轮副的啮合刚度，并分析了裂纹损伤对齿轮-转子系统振动特性的影响。Liang 等［10］建立了行星齿轮传动系统动力学模型，分析了太阳轮出现裂纹时的时变啮合刚度。故障分析方面，王鑫等［11］对比研究正常与耦合故障特征下的分岔特性，分析耦合故障引起的故障特征频率。孟宗等［12］建立了行星传动纯扭转模型，对太阳轮故障进行了固有特性分析。王子涵等［13］建立了刚柔耦合动力学模型，仿真分析了轮齿故障产生原因并模拟故障运行。

综上所述，已有的研究主要集中在降低各种误差对整体模型的影响，以及分析传动系统中各种故障信号的特点，针对故障信号传递路径的研究相对较少。齿圈作为行星齿轮传动系统中的重要部件之一，承受多种激励的共同作用，信号沿齿圈传递对系统振动响应的影响不容忽视，特别是出现太阳轮裂纹故障时，分析故障信号更为复杂。因此，研究考虑信号传递路径的行星齿轮传动系统太阳轮不同故障损伤程度的振动响应对故障诊断具有重要意义。

鉴于此，本文建立了行星齿轮传动系统动力学模型，分析了内齿圈在太阳轮裂纹故障下受到的故障激励作用，建立了考虑信号传递路径时变效应的内齿圈有限元模型，求解内齿圈的振动响应，研究在传递路径影响下，太阳轮裂纹故障振动响应的变化趋势。

1 系统动力学模型构建

以SQI 公司生产的风力发电机组试验台行星齿轮变速箱作为研究对象，行星齿轮组由太阳轮、内齿圈、行星架以及4 个相同的行星轮沿圆周方向均布的2K-H 行星齿轮传动系统构成，如图1 所示。行星齿轮组具体参数如表1 所示。

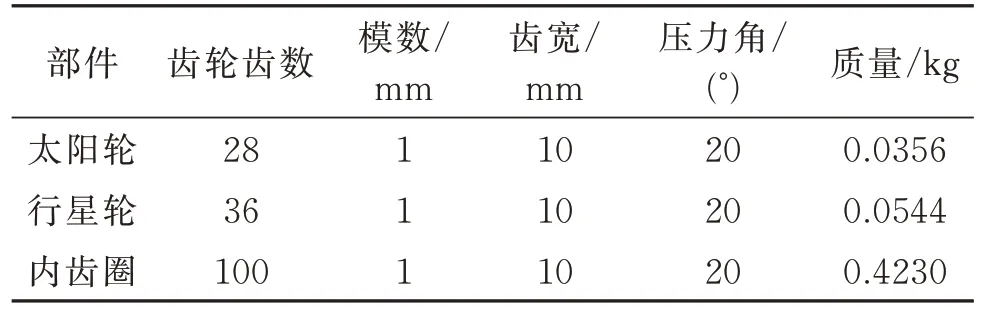
表1 传动系统参数Tab.1 Transmission system parameters

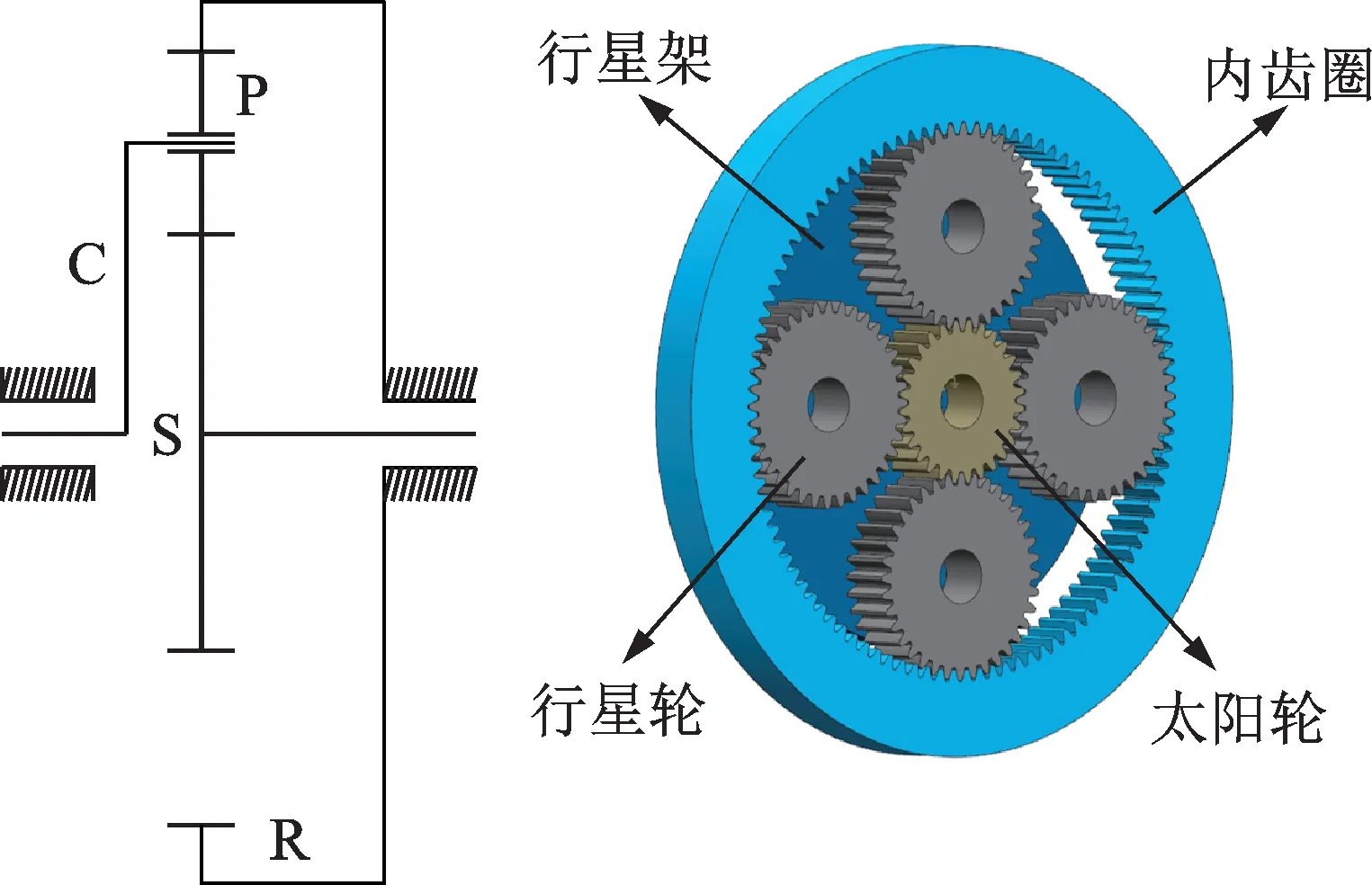
图1 行星传动系统模型Fig.1 Planetary drive system model

构建行星齿轮传动系统动力学模型，如图2 所示。太阳轮与行星轮、行星轮与内齿圈之间采用具有时变刚度的弹簧联接，模拟啮合单元的啮合过程；内齿圈上均匀分布着8 个固定支撑，kr为支撑刚度；ks，kpi和kc分别表示太阳轮、行星轮和行星架的扭转刚度；krpi，kspi分别表示行星轮与内齿圈、太阳轮与行星轮之间的时变啮合刚度，其中i=1，2，3，4；θpi为不同行星轮的扭转角微位移，其中i=1，2，3，4；θr，θc和θs分别表示内齿圈、行星架和太阳轮的扭转角微位移；wpi和vpi分别表示不同行星轮沿中心线的径向、切向微位移，其中i=1，2，3，4；ksθ，kcθ分别表示太阳轮与行星架的扭转刚度；xs，xr和xc分别表示太阳轮、内齿圈和行星架的横向微位移；ys，yr和yc分别表示太阳轮、内齿圈和行星架的纵向微位移。

建模过程中，不考虑模型的装配误差、齿侧间隙、摩擦力等因素，内齿圈和行星轮的扭转微位移和平移分解至两者之间的啮合线上，则沿啮合方向的啮合力计算如下：

式中φpi为第i个行星轮的相位角，αi为第i个行星轮与内齿圈的啮合角（i=1，2，3，4）；Rr，Rpi分别为内齿圈基圆半径、行星轮基圆半径。

行星轮与内齿圈啮合单元动力学微分方程如下：

式中Ir为内齿圈转动惯量；mr为内齿圈质量；ηrpi为啮合单元沿啮合线弹性变形。则可简写为：

式中M为内齿圈质量阵；krp为啮合单元时变刚度阵；kr为内齿 圈支撑 刚度阵；krθ为内齿 圈扭转刚度阵；U为位移矢量。

2 故障刚度计算

研究太阳轮裂纹故障对行星齿轮传动系统的影响，先确定裂纹故障主要引起啮合刚度的哪些参数变化。当太阳轮齿齿根位置出现裂纹时，裂纹的深度、角度导致转动惯量、故障截面积随之变化，而弯曲刚度、剪切刚度的计算需考虑故障转动惯量、故障截面积的影响，因此故障啮合刚度计算公式为：

式中Kd为剪切刚度，Ke为弯曲刚度，Kg为径向压缩刚度，Kj为赫兹接触刚度，Km为基体柔性刚度。

故障转动惯量、故障截面积的计算公式为：

式中e为裂纹深度；gc为裂纹角度；hx，hc等参数见图3。

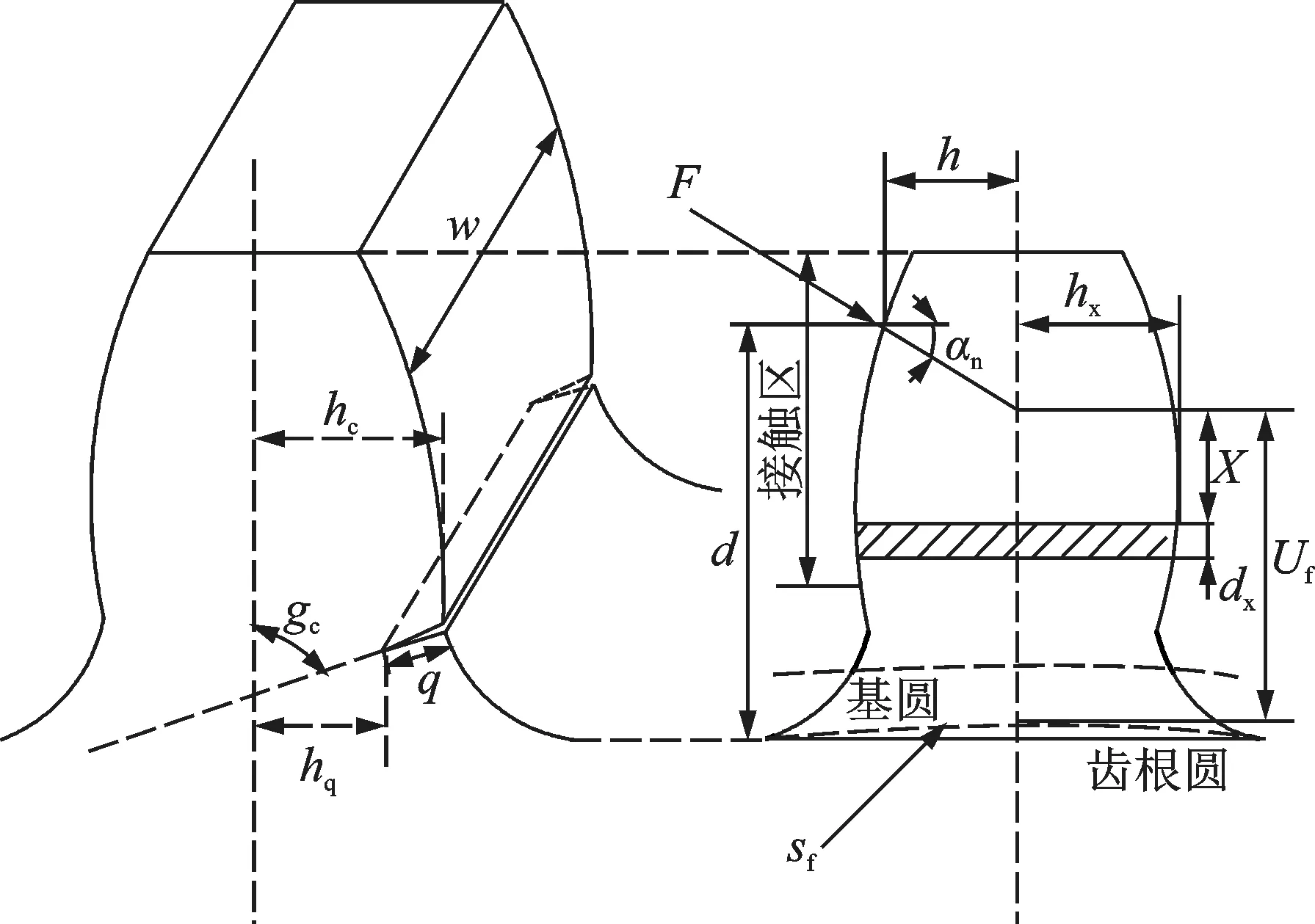
图3 齿裂纹示意图Fig.3 Schematic diagram of tooth crack

轮齿齿根位置出现裂纹，齿轮转动惯量以及故障截面积发生改变，轮齿模型具有更大柔性，因此啮合刚度相对减小，且随着裂纹深度不断增加，啮合刚度不断降低，轮齿啮合刚度随裂纹深度变化如图4所示。

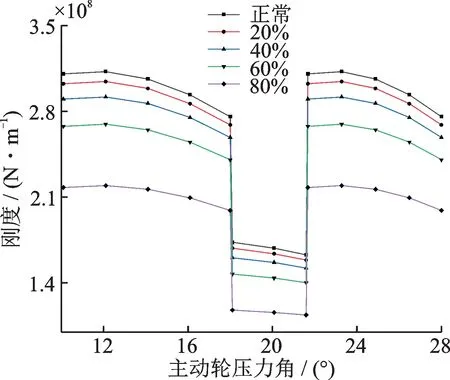
图4 轮齿啮合刚度Fig.4 Gear tooth meshing stiffness

3 裂纹故障动载荷分析

在设定输入转速为600 r/min，负载为500 N·m的情况下对系统动力学模型进行仿真，并对比分析正常动载荷和裂纹动载荷两种工况。

如图5 所示，正常工况下，行星传动系统具有对称性，所提取的动载荷呈现周期性波动，正常工况下峰值为2173.21 N，谷值为2120.86 N，均值为2149.47 N，波动幅值为23.74 N，周期T=0.00457 s。相较于正常工况，故障工况下的动载荷时域依然呈现周期性波动，在太阳轮裂纹故障因素的影响下，提取的动载荷来自于四个行星轮与内齿圈的接触，分别为接触1，2，3，4。太阳轮故障齿与某一行星轮开始啮合，齿轮之间啮合动载荷受故障齿影响骤减，与此同时其余三个行星轮与太阳轮的啮合动载荷受故障影响骤增，此时故障动载荷平均值为2145.61 N，太阳轮与行星轮动载荷的变化使行星轮与内齿圈动载荷随之变化，太阳轮故障齿处依次与四个行星轮啮合即为一个故障周期，即0.128 s。

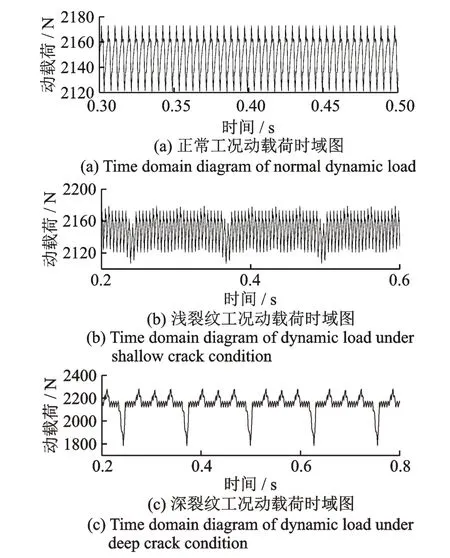
图5 不同工况动载荷时域图对比Fig.5 Comparison of dynamic load time domain diagrams under different working conditions

由物理模型参数可计算得出太阳轮相对旋转频率为：

式中ns为太阳轮转速；nc为行星架转速。

由时域图可知，随着裂纹出现至不断加深，太阳轮每旋转1 周啮合力骤减1 次、突增3 次，所以其傅里叶频谱图中除了啮合频率frp及其备频nfrp（n=1，2，3，4）以外，还包括三种故障信号，其故障频率分别为fsc=7.81 Hz，2fsc=15.62 Hz，3fsc=23.43 Hz（如图6 所示）。从低频带放大图中可以看到，低频带分别在fsc，2fsc，3fsc处出现明显幅值波动，而4fsc处出现频率耦合，幅值相对减小。对比浅裂纹、深裂纹故障工况与正常工况的频域图，故障导致自低频段开始，每个故障周期出现明显幅值增加，频域图出现大量边频带，故障边频带出现在nfsc处，而随着裂纹深度的加深，低频段的幅值也不断增加。

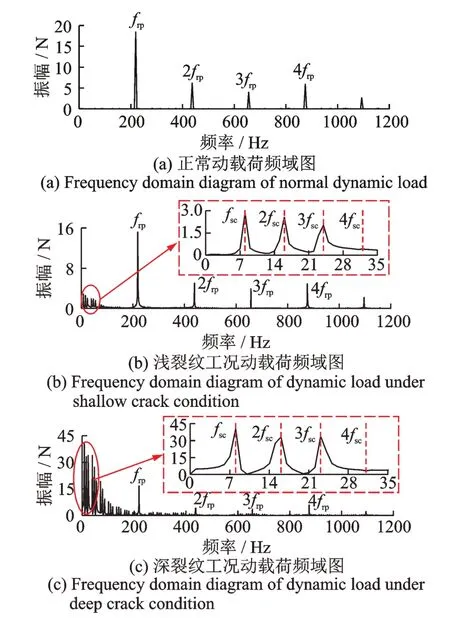
图6 不同工况动载荷傅里叶频域图对比Fig.6 Comparison of Fourier frequency domain diagrams of dynamic load under different working conditions

4 考虑传递路径下的振动响应求解

考虑信号传递路径时，信号应具备时变效应［14］，而时变效应的出现，是由于行星传动系统中四个行星轮安装于行星架固定位置，运行过程中，行星架除了自转之外，同时带动行星轮公转，各行星轮与内齿圈的啮合点与传感器之间的距离随时间周期性变化，引起了振动信号的调制，行星轮系振动信号频谱中出现行星架转频成分的边频带。因此，建立系统动力学模型作为未考虑传递路径时变效应的对照组，提取行星轮与内齿圈之间接触位置的动载荷信号，其接触相对行星轮静止，进行动载荷傅里叶频谱分析，主要成分为啮合频率及其倍频，无行星架运行振动传递路径时变效应具备的行星架转频成分，继续采集对照组模型内齿圈上两支撑中间齿齿根位置的振动信号，此时信号采集位置固定，且满足行星轮与内齿圈啮合点与信号采集点距离随时间周期性变化，采集的信号傅里叶频谱成分仍为啮合频率及其倍频。分析其原因，对照组模型中内齿圈为刚性模型，在不同位置的激励同时作用下，内齿圈作为一个刚性整体同时振动，不能准确反映行星架信号传递路径时变效应。为此，建立考虑传递路径时变效应的柔性内齿圈有限元模型。

行星齿轮传动系统各部件之间啮合关系复杂，为简化计算，同时保证计算结果的正确性，网格划分如图7（a）所示，加密接触区的网格；按轮齿承载接触分析（LTCA）等分动载荷，将某一齿上所受的动载荷12 等分，载荷施加位置如图7 所示，通过将动载荷不断施加于内齿圈上的接触齿面实现等效行星轮与内齿圈啮合过程。

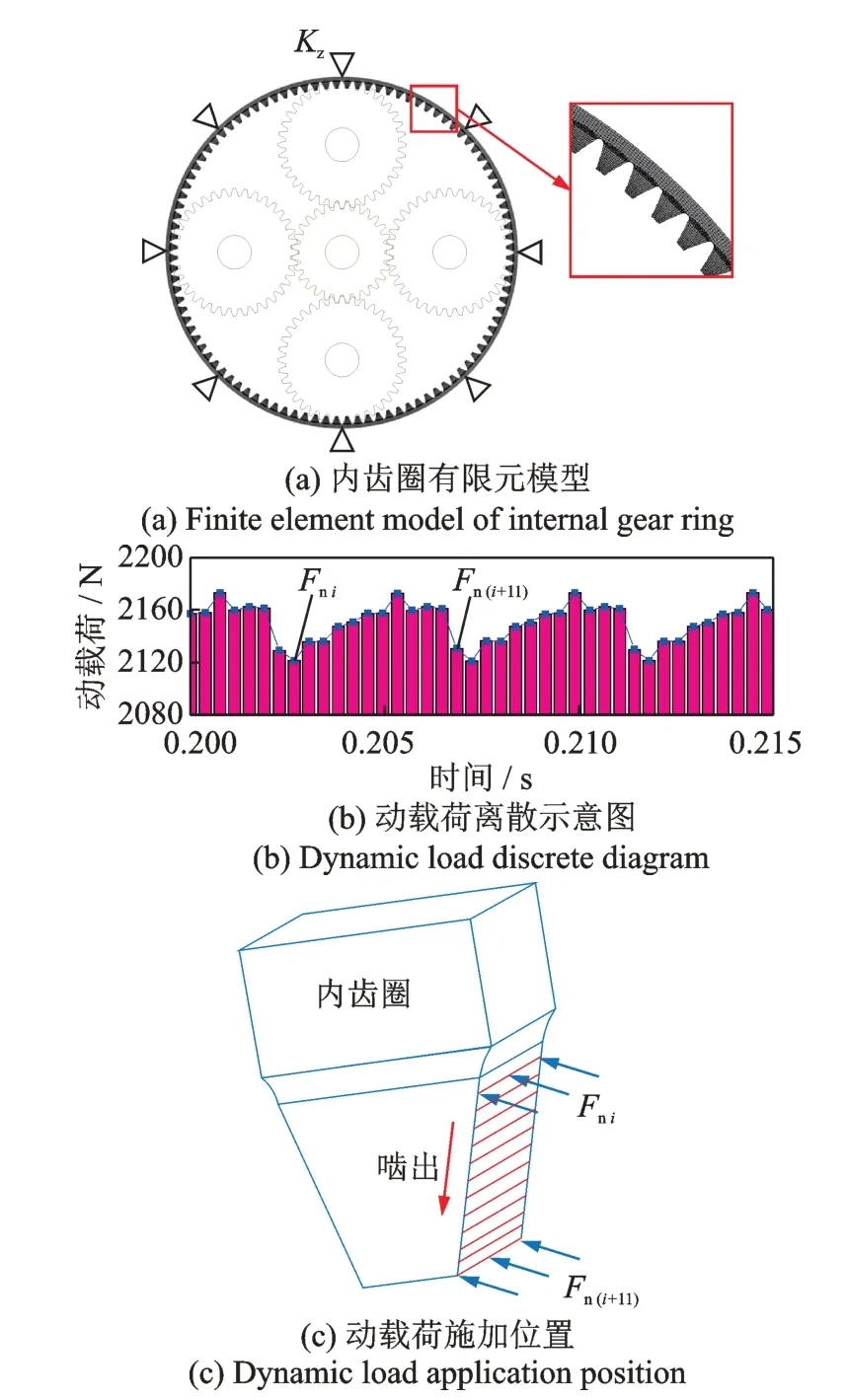
图7 有限元模型以及动载荷施加示意图Fig.7 Finite element model and schematic diagram of dynamic load application

在啮合激励作用下的内齿圈动力学方程为：

式中M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；v为节点的位移向量；G为外载荷矩阵。

对有限元模型模态提取，选择前50 阶模态矩阵进行解耦，再采用Newmark-β 时间积分法对式（9）进行求解。

对考虑传递路径的振动信号进行傅里叶频谱分析，如图8 所示，频谱成分中啮合频率附近出现了以4n倍行星架转频fc为调制频率的调制现象（n为正整数），且行星架转频的倍频与啮合频率及其倍频耦合。综上所述，振动信号在传递路径的影响下出现时变效应，验证了所建立的有限元模型能有效反映信号在路径中的传递规律。

图8 振动响应傅里叶频域图Fig.8 Fourier frequency domain diagrams of vibration response

5 故障振动响应分析

传感器安装位置如图9 所示。太阳轮故障传递路径大致分为三种，太阳轮-太阳轮轴-箱体-传感器为路径一；太阳轮-行星轮-行星架-行星架轴-箱体-传感器为路径二；太阳轮-行星轮-内齿圈-传感器为路径三；根据路径一、二的距离不会随着故障啮合位置的变化而变化的特点，传感器固定时，故障信号经由路径一、二传递不受啮合位置变化的影响［15］。而路径三具备随啮合位置变化传递距离也不断变化的特点，可能的啮合位置如图10（a）～（d）所示［15］。

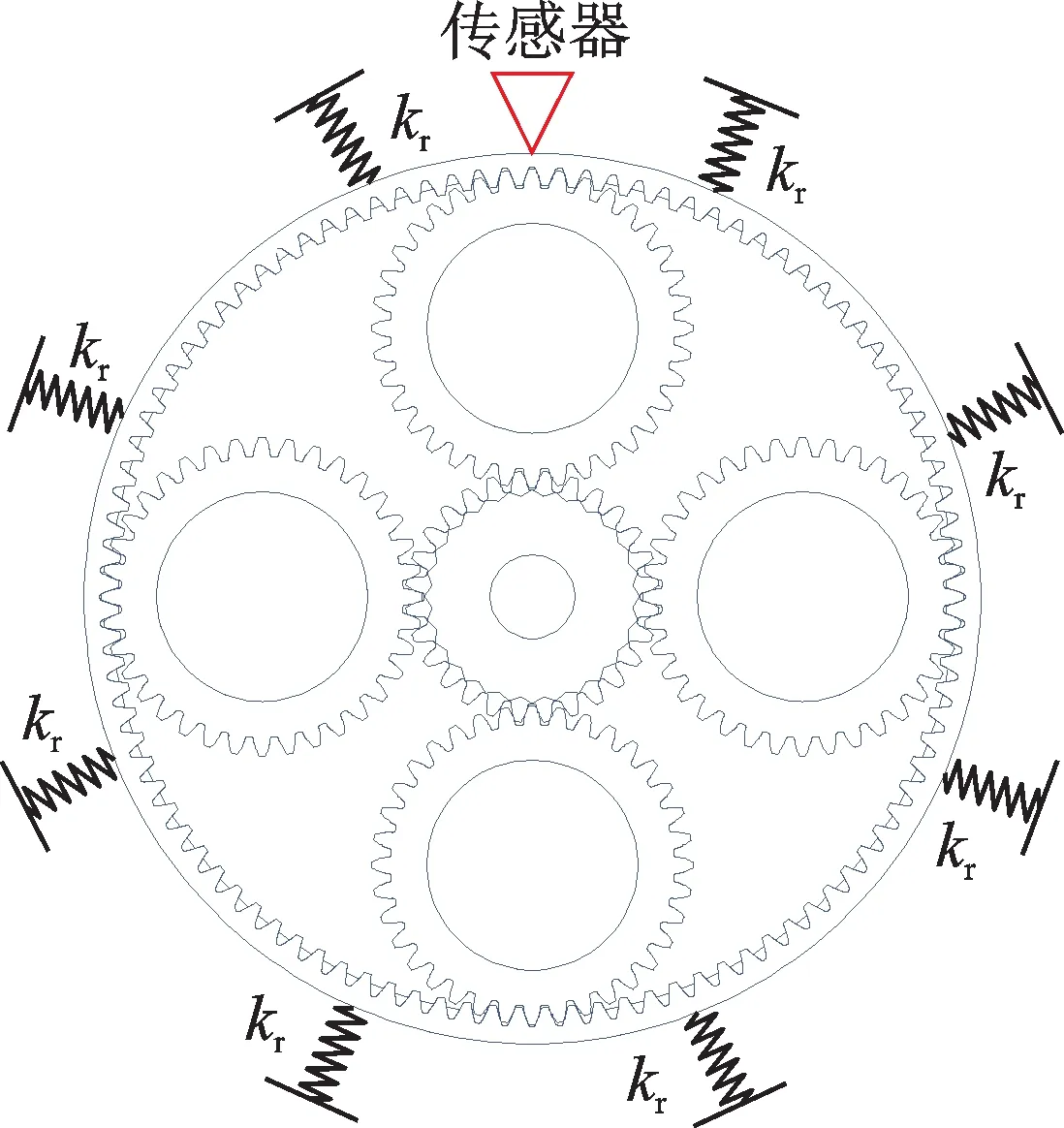
图9 传感器安装位置示意图Fig.9 Schematic diagram of sensor installation position

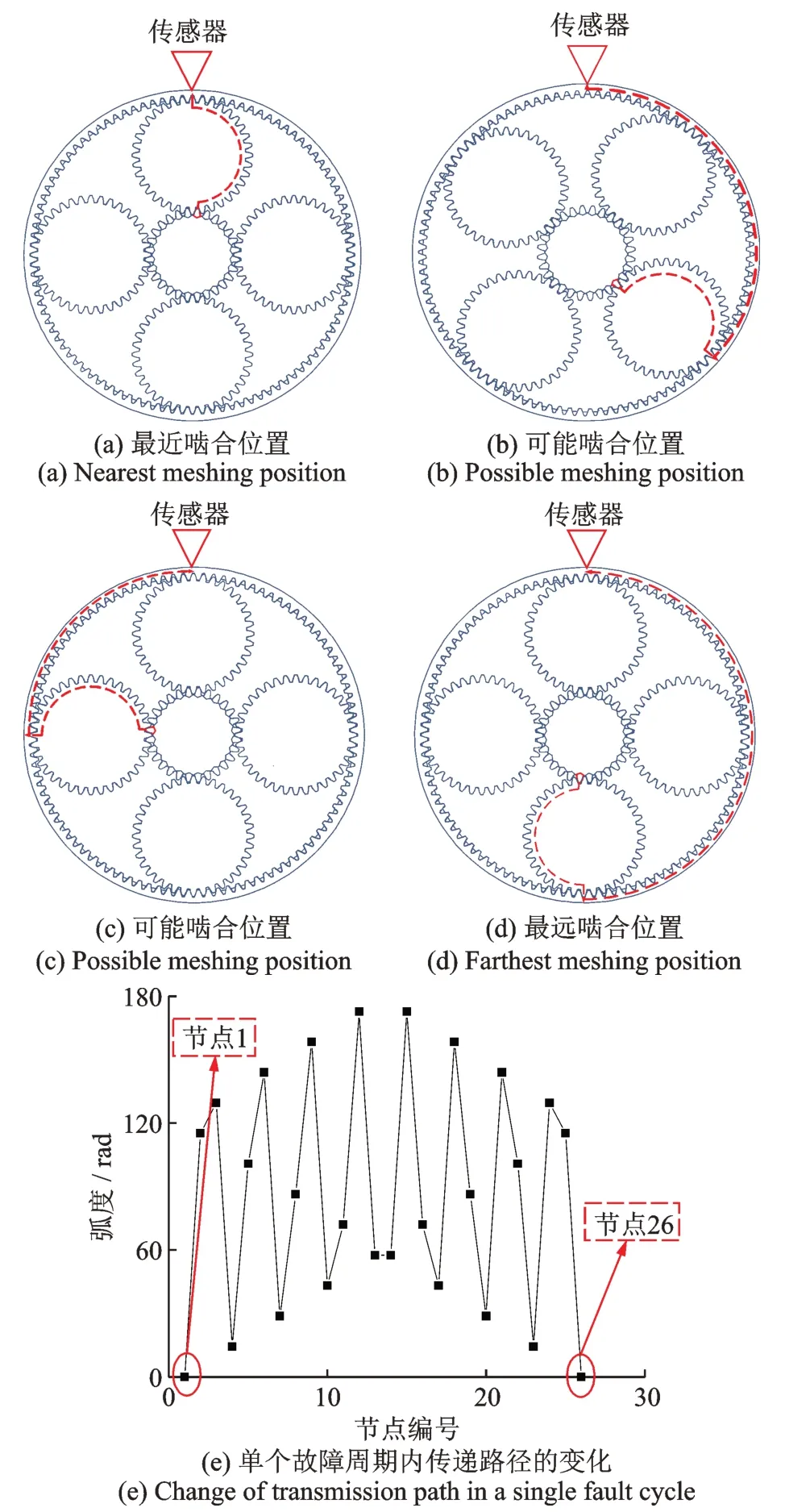
图10 不同啮合位置下的传递路径变化示意图Fig.10 Schematic diagram of transmission path changs at different meshing positions

振动响应的分析中，将最短传递路径作为主要传递路径考虑，行星轮与内齿圈啮合位置位于内齿圈左侧时，左侧至传感器距离最短；啮合位置位于内齿圈右侧时，右侧至传感器距离最短。

已知传递路径距离随太阳轮故障齿运行中依次与不同行星轮啮合而不断变化，由式（8）可求出当前转速下的太阳轮相对行星架的旋转频率fsc，行星传动系统结构为四行星轮对称分布，则太阳轮上故障齿与相邻两行星轮啮合时间间隔ts为：

式中N为行星轮个数。

引入太阳轮裂纹故障进行仿真，采集相同位置振动响应，已知四个不考虑加工误差的行星轮均布在太阳轮四周，与太阳轮啮合状态相同，则太阳轮故障啮合最小周期即为tg：

依据文献［15］，仿真中设定四个行星轮不考虑制造误差，因此最小故障周期tg是伪潮汐周期［14］，实际制造过程中存在误差，最小故障周期为潮汐故障周期4tg。

当传感器位置固定时，以太阳轮故障齿与某一行星轮啮合过最短传递路径（节点1）为初始位置，在与下一次啮合过最短传递路径（节点26）之间间隔时间tg内，故障齿还将与不同行星轮啮合过25 次，传递路径距离（用弧度表示）随之变化，如图10 所示。由图10（e）可知，在传递过程中存在两次传递距离达到最远位置。

如图11（a）所示，无故障工况下振动信号呈现周期响应，随着行星轮不断接近传感器所在位置，振动不断增大，当行星轮啮合过传感器以后，振动随之减弱。由图11（a）可知，无故障工况下最小振动响应周期为Tx=0.114 s，为1/4 的行星架转动周期，时域波形始终在零点上下波动。引入太阳轮齿裂纹故障，对比故障时域包络图（图11（b），（c））可知，太阳轮故障导致最小振动响应周期变为故障周期tg，故障周期tg约为7Tx。

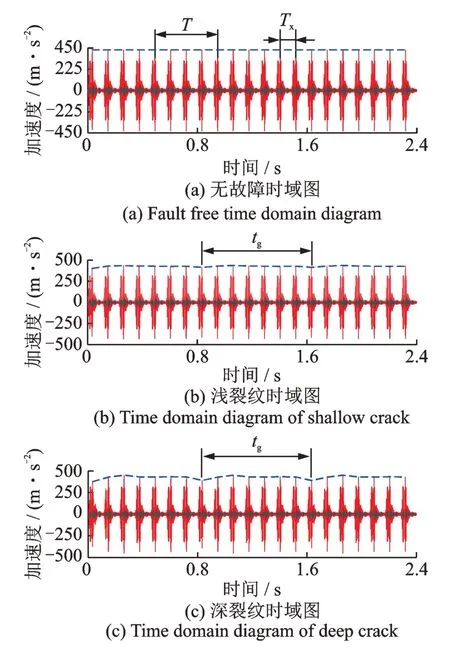
图11 振动信号时域图Fig.11 Time domain diagrams of vibration signal

取相邻两支撑作为故障啮合位置进行分析，将两支撑中的12 齿分别编号，如图12（a）所示。对比12 齿正常与故障工况的加速度均方值变化。当啮合位置靠近支撑时，啮合位置受故障影响最大，且随着故障信号传递，两支撑内各齿的加速度均方值均减小。当啮合位置处于支撑中间时，受故障影响位置最大的仍为啮合位置，其余各齿的加速度均方值仍减小。因此在故障信号传递至齿圈上后，在齿圈上两支撑中间，故障振动信号对故障啮合点的影响最大，并且沿着齿圈向周围扩散，影响逐渐减小。

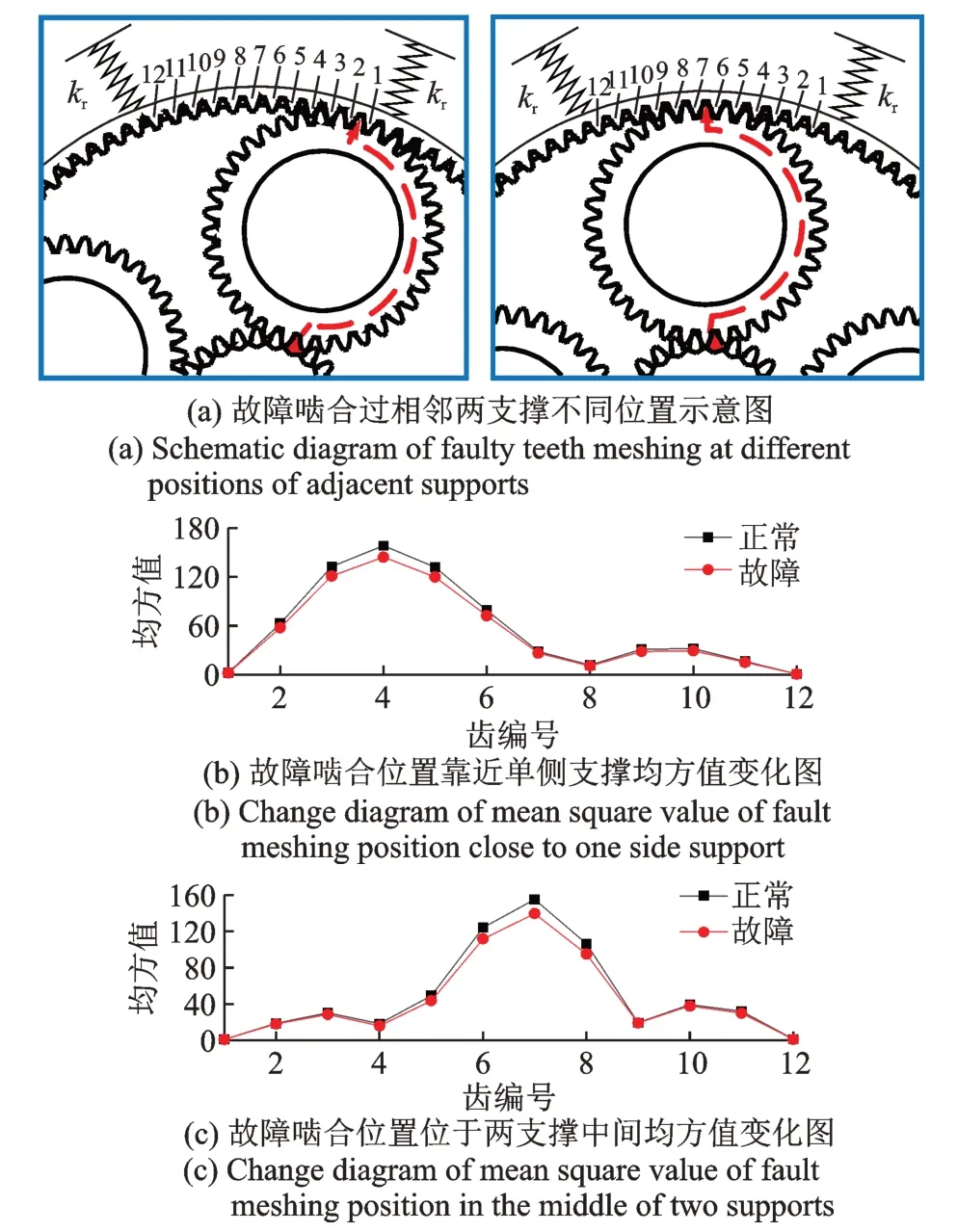
图12 故障齿啮合过相邻两支撑不同位置对均方值的影响分析Fig.12 Analysis of the influence of fault teeth meshing over two adjacent supports at different positions on the mean square value

动载荷分析中，已知当太阳轮故障齿与某一行星轮啮合时，此行星轮与内齿圈接触动载荷会出现骤减；同时，另三个行星轮与内齿圈接触动载荷均出现骤增，分析仿真结果如图13 所示。每次太阳轮故障齿与行星轮啮合时，故障信号经由齿圈上不同啮合点沿传递路径传递至传感器，时间间隔为ts，取单个故障周期tg内25 个故障啮合位置的信号均方值，分析在传递路径影响下，传感器采集的故障信号变化规律。发现单个故障周期内信号均方值并不是随着传递距离越近，信号减弱越严重；考虑传递路径时，除了故障齿啮合导致的振动信号传递之外，另三个行星轮啮合传递的故障信号也被传感器采集，导致采集的振动响应出现调制，故障振动响应出现了随机增强或减弱。因此，每隔ts采集到的信号在故障振动响应影响下均会出现明显波动，但波动趋势并没有随着传递路径距离变化而变化。

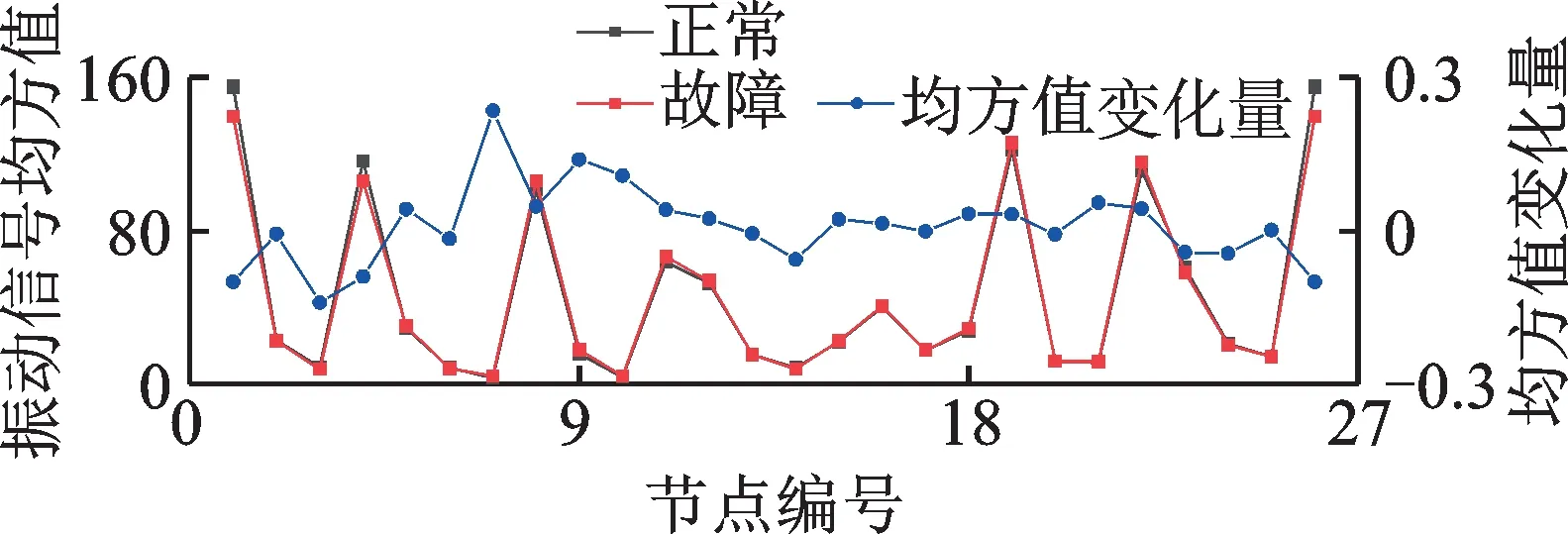
图13 单个故障周期振动信号均方值对比图Fig.13 Comparison chart of the mean square value of the vibration signal of a single fault cycle

如图14 所示，太阳轮出现裂纹故障时，已知故障周期tg=0.8 s，故障傅里叶频域图低频带相比正常工况出现大量n倍故障频率成分的波动幅值（n为正整数），在啮合频率附近出现了以故障频率fg为间隔的边频带，且随着裂纹深度的增加，frp-nfg和frp+nfg的振幅也随之增大。由于行星架转频的4 倍频为故障频率fg的整数倍，因此部分故障频率边频带与行星架转频的倍频耦合。

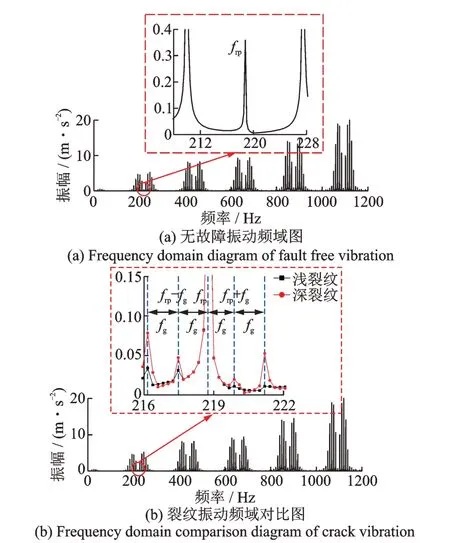
图14 振动信号傅里叶频域图Fig.14 Fourier frequency domain diagrams of vibration signal

低速运行时正常工况径向位移如图15所示，径向位移幅值较小，则行星传动系统运转较为平稳。对比故障工况下的径向位移图可知，低速运行时故障振动幅值增大，太阳轮故障导致整个传动系统稳定性降低，并且这种影响会随着转速的增加而相应增大。

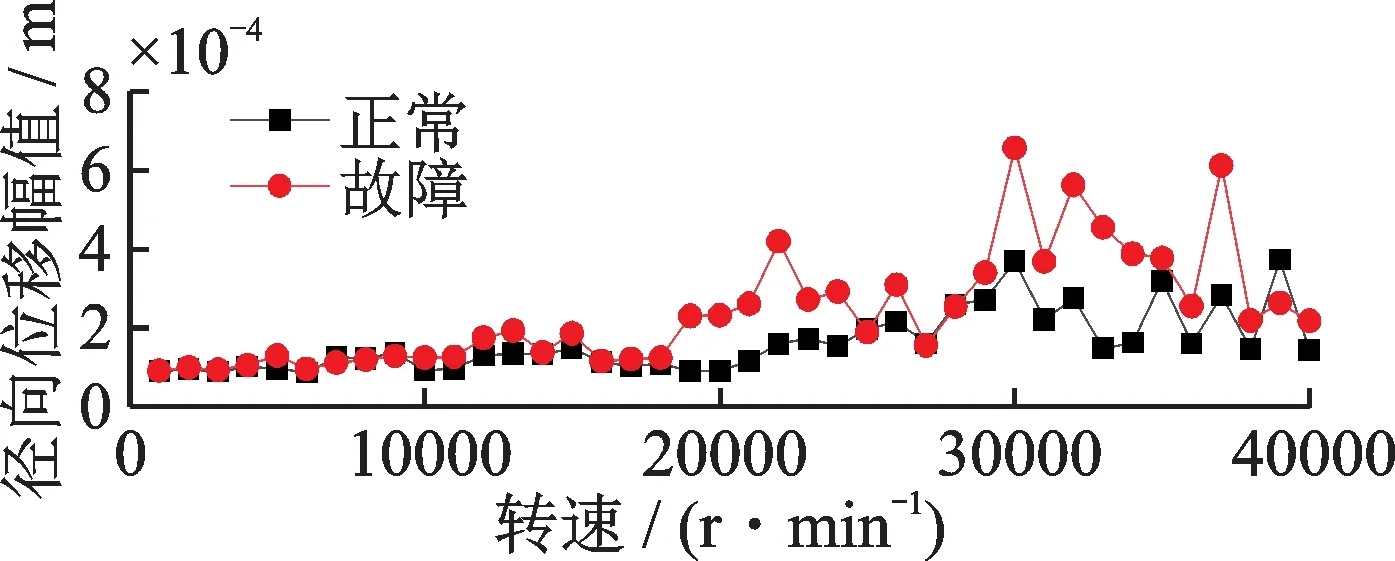
图15 不同转速下的径向位移幅值图Fig.15 Diagram of radial displacement amplitude at different speeds

6 实验信号验证

采用SQI 公司生产的风力发电机组实验台进行实验，实验台由磁粉制动器、二级定轴减速器、风电行星增速器和驱动电机组成，采集模块为Dewesoft数据采集系统，采样频率为20000 Hz。如图16所示。

图16 故障信号采集实验台Fig.16 Fault signal acquisition experiment platform

采集的原始实验数据如图17 所示，原始振动信号时域成分中包含大量冲击信号。对其进行频谱分析，频域成分中在啮合频率附近存在大量边频带，行星架转频、啮频及啮频倍频成分明显，边频带的成分难以区分，故障特征被噪声掩盖，因此，对原始故障信号进行特征提取。

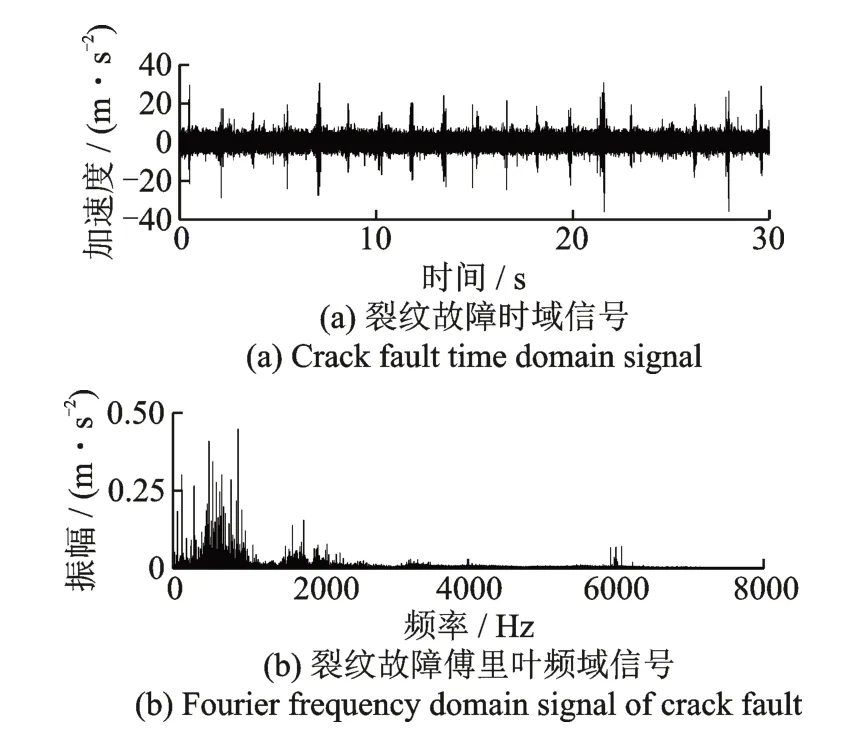
图17 故障实验信号Fig.17 Fault test signal

Antoni 提出的快速谱峭度法（FSK），能准确反映强噪声的振动信号瞬时冲击成分［16］，具体信号处理流程如图18 所示。

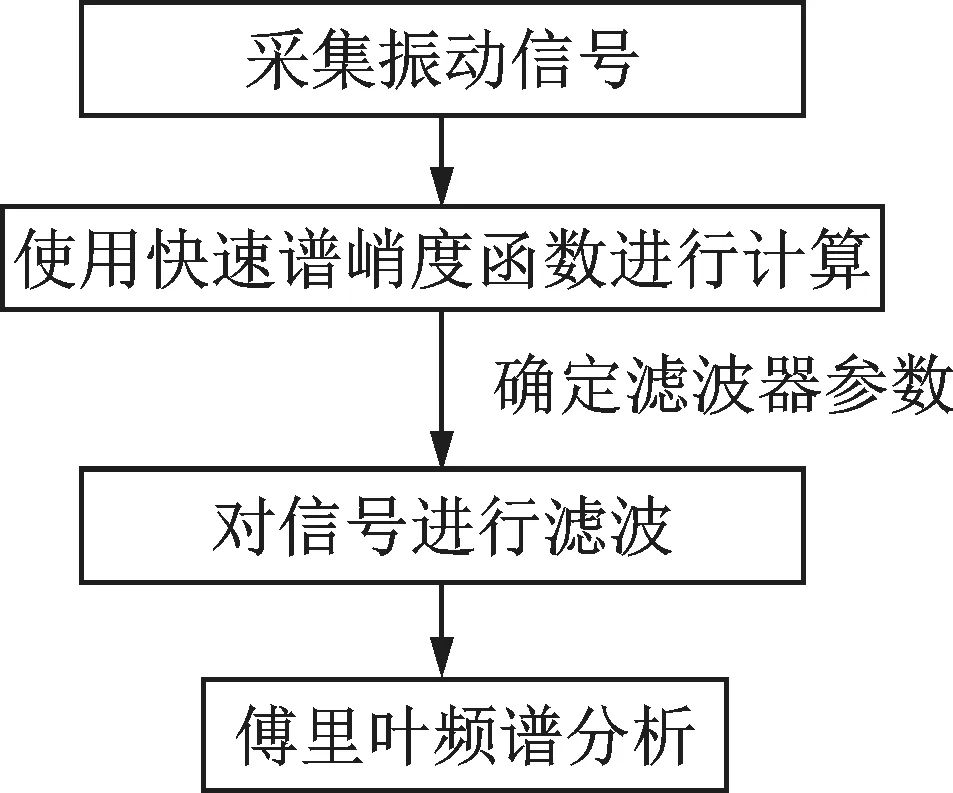
图18 信号处理流程Fig.18 Signal processing flow

对实验信号进行快速谱峭度分析，采用FSK 提取故障信号特征，结果如图19 所示。

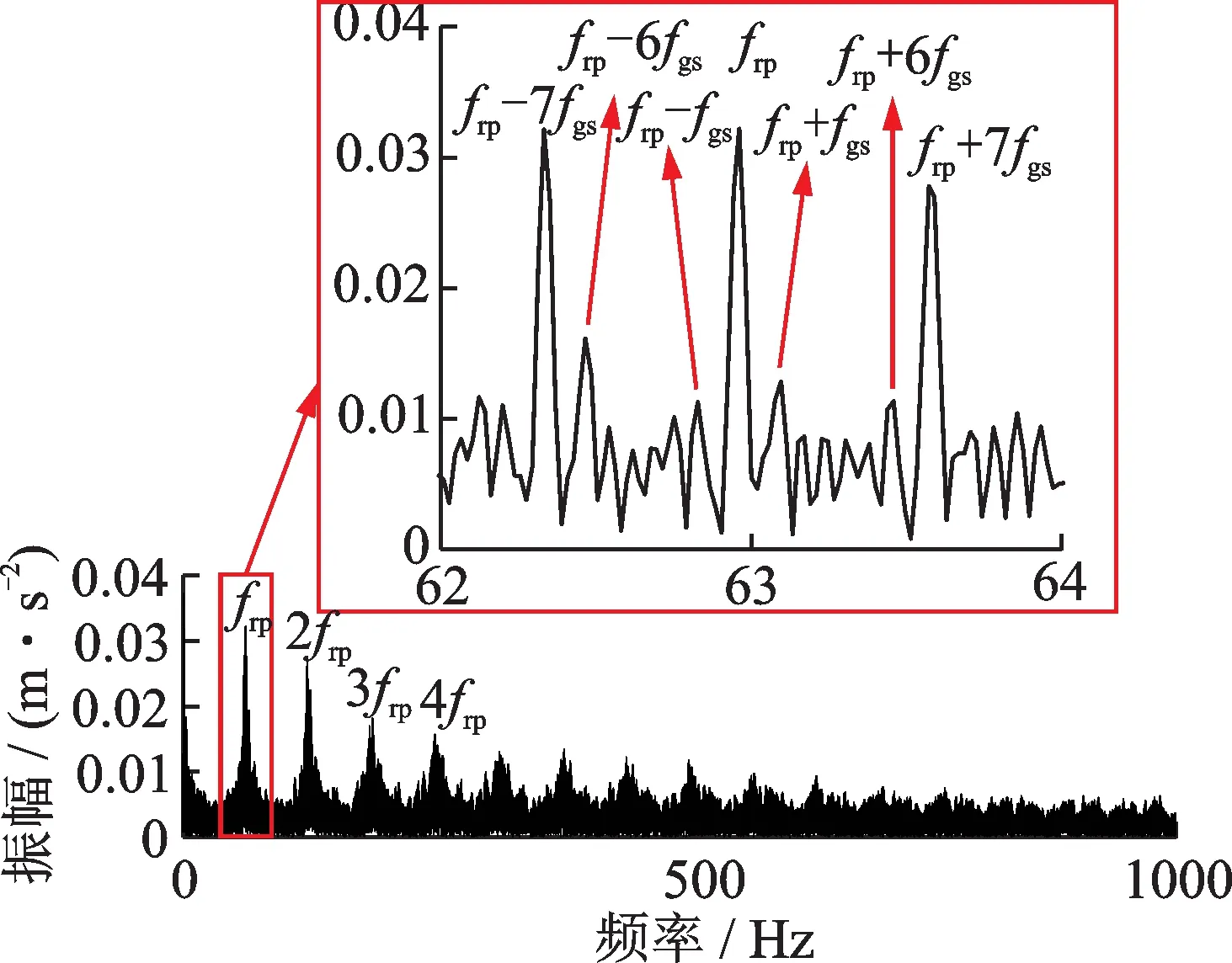
图19 太阳轮裂纹故障实验信号Fig.19 Experimental signal of crack fault of sun gear

分析实验信号，由图19已知实验信号输入转速为174 r/min，由于实际制造中不可能制造出完全一致的四个行星轮，实验信号应采用潮汐周期4tg作为故障周期，对应太阳轮故障仿真信号中故障频率（1/4）fg，即fgs。因此，实验信号中故障频率间隔的边频带frp±fgs对应仿真信号中frp±fg，验证太阳轮裂纹故障仿真信号中故障频率间隔的边频带，其中实验信号啮合频率的边频带中fgs，6fgs和7fgs几个成分较为明显。

7 结论

以行星齿轮传动系统为研究对象，针对太阳轮齿根裂纹故障情况，采用有限元法建立齿圈结构动力学分析模型，对比分析了考虑与未考虑传递路径的齿圈振动响应，开展了试验测试与仿真结果的对比分析，得出如下结论：

（1）仅考虑与太阳轮故障齿啮合的行星轮的传递信号，在路径中的传递随距离增加呈现不断衰减趋势；当考虑所有行星轮的传递信号，故障信号出现调制现象，随传递距离增加呈现衰减或增加趋势。

（2）随着太阳轮裂纹故障程度的加深，故障振动信号频域边频带中故障频率的幅值不断增加。

（3）随着转速的升高，内齿圈振动幅值受太阳轮裂纹故障影响随之增大。低速工况下太阳轮故障引起齿圈振动幅值增大，导致行星传动系统稳定性降低，并且这种影响会随着转速的升高而不断增加。