一种具有能量俘获自参数摆动力吸振器的设计及参数影响分析
陈晓哲,焦志成,石加联
(1.东北大学秦皇岛分校控制工程学院,河北 秦皇岛 066004;2.辽宁科技大学机械工程与自动化学院,辽宁 鞍山 114051)
引言
目前,振动抑制的主要方法有:主动控制、被动控制、混合控制和半主动控制[1]。上述方式中,被动控制不需要外部能源,仅通过自身阻尼消耗振动能量进而实现振动抑制,所以其结构简单,易于实现,工程应用也最为广泛。
动力吸振是一种常见的被动减振方式,其原理是在振动过程中通过动力吸振器吸收振动系统的能量来降低主系统的振动[2]。基于该吸振原理,学者们对动力吸振器的工程应用展开了研究。杨恺等[3]设计了一种主被动电磁式动力吸振器,其实验结果表明,该吸振器在主动控制后对共振和非共振模态抑振效果更好,可用于抑制柔性结构的多模态振动。邢昭阳等[4]提出了一种向振动控制系统中引入负刚度的动力吸振器,系统在低频区的响应由于负刚度特性被放大,减振性能提高。代晗等[5]在反共振点处对一种接地负刚度时滞反馈控制的动力吸振器进行了优化,结果表明该类吸振系统抑振效果优越。
上述研究中,只考虑了对主结构的振动进行抑制,却没有考虑到对这些振动能量的回收。实际上,通过换能器不仅可以将多余的振动能量转化为电能进行储存,为一些微型传感器等设备提供电能,还能减小振动给设备带来的危害。根据能量间不同的转换机制,振动能量俘获系统可以分为静电式、电磁式、压电式、磁致伸缩式、摩擦起电式以及它们的混合式[6]。在这些机制中,电磁式振动能量俘获系统结构简单、发电量大、输出阻抗小,已经成为重要的振动能量采集方式之一,受到国内外学者的广泛关注[7]。例如,陈春明等[8]利用杠杆机构,放大了磁铁与线圈之间的相对位移,设计了一种新型电磁式振动能量采集器,通过与等效的线性振动能量采集器对比发现,相同激励下该系统的能量采集效率是线性采集器的1.76 倍。刘仲琳等[9]采用磁化电流法分析非线性磁力,探索随机激励下双稳态振动的磁场变化对感应电动势的影响规律。曹淑瑛等[10]对电磁式振动能量的采集电路进行了系统地分析,重点研究了在低输入电压下如何实现高效的电能转换。
虽然振动能量回收机理成功地应用在动力吸振器的设计上,但是对于动力吸振器的研究常常只针对某一特定频率进行回收效率方面的探讨。由于工程中的振动频带往往以较宽形式存在,导致实际应用中回收效率并不高。因此,设计合理的动力吸振器结构,并拓宽其抑振频带,提高其回收效率是一个亟待解决的问题。考虑上述需求,本文基于自参数摆系统,将振动抑制和能量回收两种工程需求结合在一起,设计了一种具有能量回收功能的自参数摆动力吸振器,并建立了该振动系统的动力学模型,通过理论分析和数值仿真研究了设计参数对系统抑振性能和俘能性能的影响。
1 系统的结构设计及数学模型
1.1 结构设计
图1(a)为本文所提具有能量俘获功能的自参数摆动力吸振器的结构示意图。与传统摆类吸振器不同的地方在于此结构采用封闭线圈来代替子结构摆,并且在摆的运动平面上,摆的两侧对称装有两块大小相同的强磁铁。当系统受到外部激振时,可以将主结构y方向上直线运动的振动能量传递给子结构线圈ψ方向上的摆运动。因为线圈切割强磁铁的磁感线时会产生感应电流,所以该系统可以在抑制振动的同时也对振动能量进行回收。
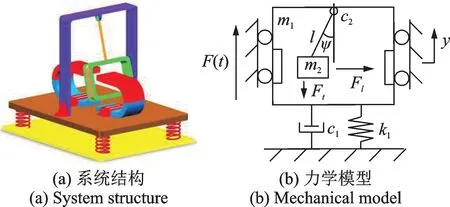
图1 自参数摆动力吸振器Fig.1 The model of auto-parametric pendulum dynamic vibration absorber
1.2 数学模型
图1(b)为该系统的力学模型,其主要包括一个主质量块m1和一个附着在主质量块上的线圈摆m2。主质量块与固定底座间由弹簧来连接,其刚度为k1、阻尼为c1。线圈m2的摆长为l,机械阻尼系数为c2,电阻尼系数为ce,摆角为ψ。一简谐激振力F(t)=F0cos(ωt)作用在主质量块上。
基于拉格朗日方程建立该自参数振动系统的运动微分方程,如下[11]:
考虑到磁力是线圈摆角ψ的函数,可以将磁力以摆角ψ近似展开[12],获得其近似表达式如下:
2 理论分析
2.1 多尺度法求解
考虑到线圈摆在平衡点ψ≈0 附近为小振荡,计算时可忽略式(4)中摆角ψ的高阶项,同时可将非线性项sinψ和cosψ用泰勒级数展开为:sinψ≈ψψ3/6+o(ψ5),cosψ≈1-ψ2/2+o(ψ4),则式(3)和(4)可进一步化简为[13]:
为研究系统的主共振和2∶1 的内共振,令Ω≈ω1+εσ,ω1≈2ω2+εσ1,其 中σ和σ1为调谐参数。应用两个不同的时间尺度T0和T1,其中Ti=εiτ,(i=0,1),ε表示一 个小参 数,设方程 的一次近似解为[14]:
将式(7)分别代入式(5)和(6),分离虚部和实部后,最终整理得:
式中ϕ1=σT1-γ1,ϕ2=2γ2-γ1-σ1T1,γ1和γ2表示系统通解中的相位角。
2.2 稳定性判断
为判断上节得到的两种平衡解的稳定性。需将非自治系统转化为自治系统,令h1=a1cosϕ1,h3=a2cos [(ϕ1-ϕ2)/2],h4=a2sin [(ϕ1-ϕ2)/2],h2=a1sinϕ1并将其代入式(8)~(11)后,可得自治系统的雅可比矩阵B及特征方程为:
基于李雅普诺夫稳定性理论,解的稳定性取决于雅可比矩阵的特征值[16]。如果其中一个特征值具有正实部,则系统的解将是不稳定的。若所有特征值的实部均为负值,则系统解将是渐近稳定的。
3 数值分析
3.1 抑振机理分析
基于理论分析,取各参数为f=0.01,q1=0.3,q2=0.1,q3=0.2,λ1=0.01,η=0.5,λ2=0.01 和ω2=0.711,分别代入式(12)和(13),把得到的结果用式(15)的稳定性条件进行判断,可得上述参数对应的系统幅频曲线,如图2 所示。其中,绿色点表示在相同条件下,用龙格库塔法求解式(3)和式(4)的数值解。从图2 可以看出,解析解和数值解的结果非常接近,这说明了解析解的正确性,也说明上述假设(摆的运动幅度较小)的合理性。
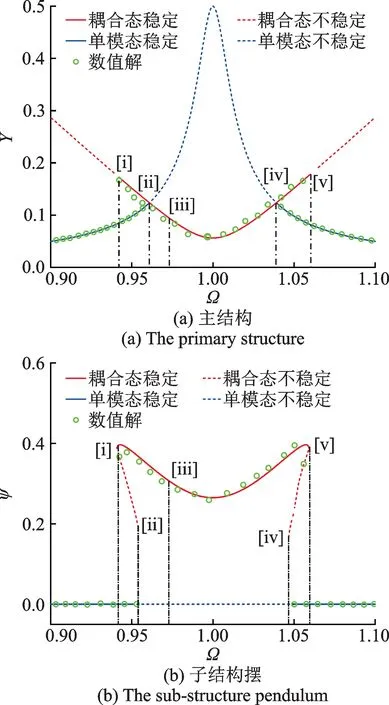
图2 幅频特征曲线Fig.2 Amplitude frequency characteristic curves
接下来分析系统的抑振性能,当横坐标Ω小于[i]值或大于[v]值时,系统处于单模态运动,即子结构线圈摆不发生摆动,此时系统只存在主质量块的运动,没有产生抑振效果。当Ω在区间值[ii]~[iv]变化时,系统处于耦合态运动,即主系统和子系统都存在运动。随着子系统产生摆动,振动能量从主系统转移到子系统。主质量块摆动的幅值变小,说明子结构摆的摆动对主质量块的运动产生了抑振效果。当Ω在区间值[i]~[ii]或[iv]~[v]变化时,此时系统存在两种稳定运动状态。系统选择在哪种稳态下运动取决于初始的外部激励条件。
观察图2(a)的幅频曲线,可知在主共振区Ω=1时主系统的振动幅值最小,子系统对主系统的抑振效果最为明显。因此,通过结构设计使外激振源的频率处于主共振区,不仅可使原系统幅值减小,而且通过摆的运动还可以将这部分振动能量转化为电能进行回收。
3.2 设计参数对抑振性能的影响
从图2 可以看出,该动力吸振器有效的工作区间是[ii]~[iv]这段频带,称其为抑振频带。该频带的宽窄是评价抑振性能的重要指标之一。因此,研究不同设计参数对抑振频带的影响,是动力吸振器结构设计的关键环节。根据式(12)和(13)中的解析式可得该非线性振动系统的幅频特征方程为:
如果直接对式(16)进行求解,过程将会十分复杂,所得结果的表达式也将非常繁琐。为使求解过程变得简单,接下来利用小参数法进行化简求解[17]。将下列参数进行摄动f=εf1,Ω=1+εΩ1,λ1=ελ,并代入式(16)中整理得:
根据式(17),可得系统的抑振频带为:
从式(18)直接可以看出,抑振频带与参数λ1成反比,与参数f成正比。为了更直观地说明参数λ1与f对系统抑振性能的影响,选择几组不同参数的组合进行定量的数值分析。图3 为主质量块的幅频图,其他参数与3.1 节相同。

图3 不同λ1 与f 时的幅频曲线Fig.3 Amplitude frequency curves for different λ1 and f
如图3 所示,当参数λ1减小或f增大时,主质量块在耦合模态下的振动幅值并不会发生明显变化,但是在单模态下运行时,系统的抑振频带则会相应地增宽,这与式(12)和(13)的结论相符合。
同时,在式(18)中,不易直接观察到设计参数q1和ω2对抑振频带的影响。为了得到最优的抑振频带,可令dΔ/dq1=0,可以得到q1和ω2的关系式为-ω2=q1。将该关系式代入式(12)和(13),进一步分析q1和ω2与抑振频带之间的关系。采用表1中的参数来计算在不同参数条件下主质量块的幅频响应曲线,如图4 所示。
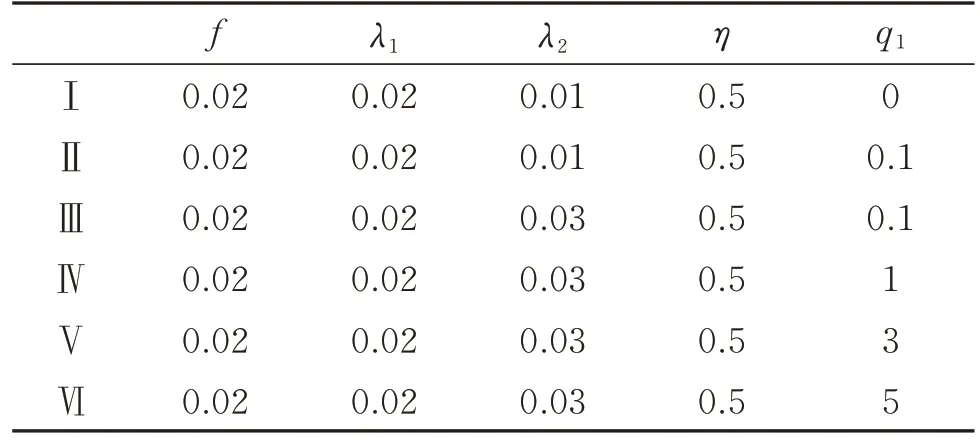
表1 频带比较的系统参数表Tab.1 Parameters for frequency bandwidth comparison

图4 不同参数的幅频响应Fig.4 Amplitude frequency response for different parameters
观察图4 中各曲线的交点,并对比I 和Ⅱ,发现相比于传统的摆类吸振器(q1=0),在增加磁力后,主质量块的振动幅值减小,抑振频带加宽。对比Ⅰ和Ⅲ也可以看出,用封闭线圈代替传统结构中的摆后,当附加磁力较小时,主质量块的振动幅值变大,抑振频带减小。这是由于线圈摆在摆动时所产生的电阻尼ce导致系统参数λ2变大,进而导致系统抑振效果变差。但对比Ⅳ,Ⅴ和Ⅵ后可知,随着附加磁力q1的增加,主质量块的振动幅值逐渐变小,抑振频带随之变宽。基于以上分析可以得出,该动力吸振器由于引入线圈摆的设计,其抑振性能相比于传统摆动力吸振器得到了一定的提高。
3.3 俘能性能机理分析
基于本设计中引入的线圈摆,该动力吸振器会将部分振动能量转换为电能。俘能器的瞬时功率P在负载电阻R上产生,可以表示为:
3.4 设计参数对俘能性能的影响
为分析设计参数对系统俘能性能的影响,取f=0.02,η=0.5,λ1=0.02,λ2=0.03,其余参数见3.1 节,来计算不同磁力q1作用下系统的平均功率曲线,计算结果如图5 所示。图中曲线均满足条件
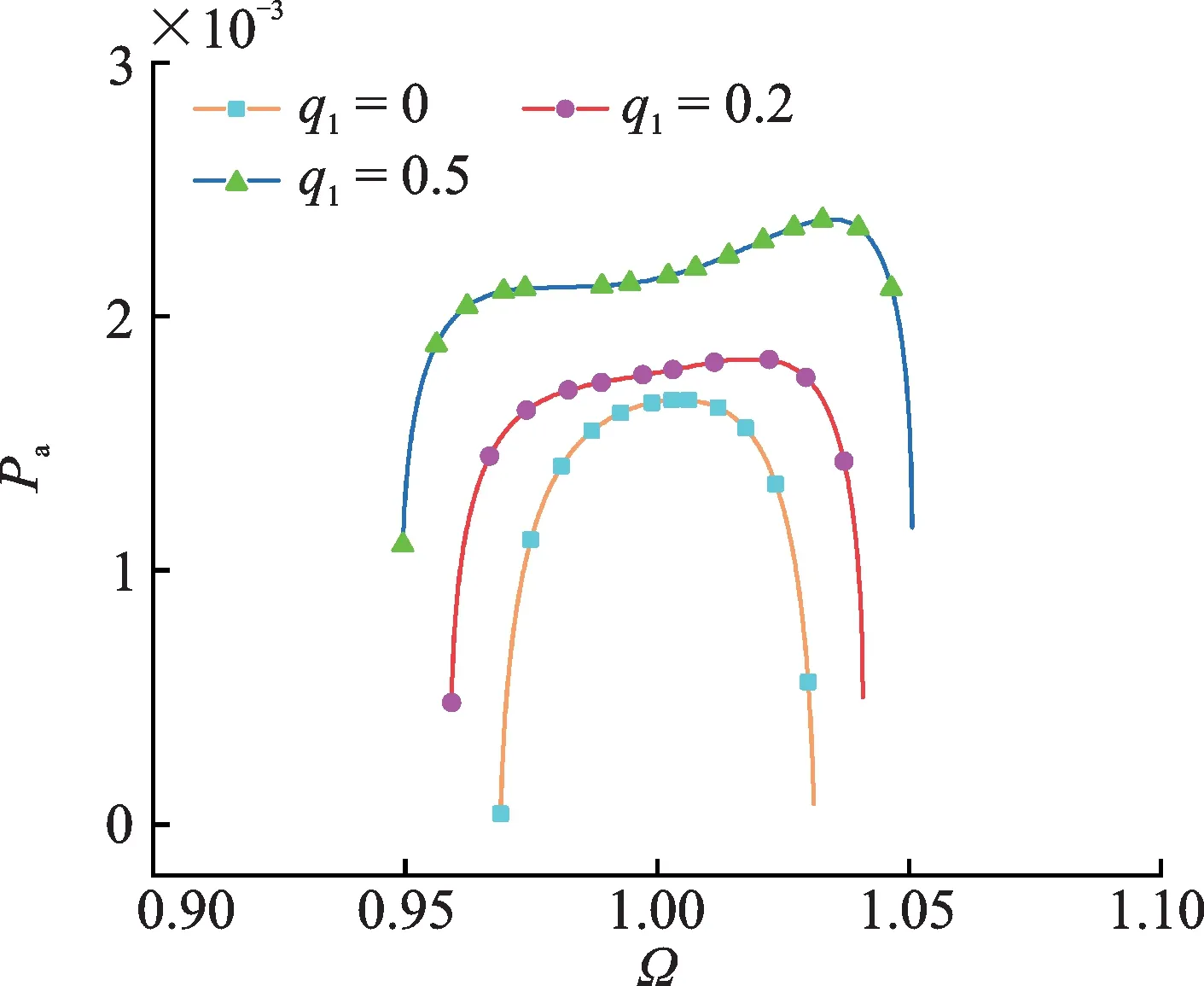
图5 不同磁力下的平均功率Fig.5 Average power for different magnetic forces
由图5 可知,随着附加磁力的增加,能量收集的幅值和带宽都在变大,该变化规律与设计参数对抑振性能的影响变化是相同的。
观察式(21)和(22)发现,当没有附加磁力q1,即q1=0 时,参数ω2的最优值为0.5。增加磁力后,即q1>0 时,参数ω2的最优值将变大,且大于0.5。因为参数ω2的增加会使主质量块的振动幅值amin减小,抑振频带Δmax变大,所以该状态下系统的抑振效果较好,并且俘获的能量也较多。
综上所述,为了使系统的抑振性能更好,在结构设计时,应取较小的参数λ1和λ2,较大的参数ω2和q1。根据1.2 节中所设的无量纲参数,上述参数的变化可通过设计较小的机械阻尼c1,c2,弹簧刚度k1和摆长l,或增加附加磁铁的磁力等来实现。
4 仿真验证
为了更直观地看出主质量块与子结构摆的耦合运动关系,计算了不同频率Ω下系统的时域曲线,如图6 所示。其中各参数同3.1 节。从图6(a)可以看出,系统此时处于稳定的单模态运动,即摆不发生摆动,也不产生抑振效果。对于图6(b),系统处于稳定的耦合状态,此时主质量块的振动幅值减小,其很大一部分振动能量被转移到摆的运动中,使主质量块的振动得到了有效的抑制。当频率接近共振频率时,此时主质量块的振动幅值最小,抑振效果最好,如图6(c)所示。

图6 时域仿真Fig.6 Time domain simulation
图6 显示了该动力吸振器从单模态(摆不发生摆动)到耦合模态(摆发生摆动,产生抑振效果)的过程。对比图2,时域仿真与理论结果在各个阶段的变化是一致的,这也验证了本文所采用的解析方法是正确和有效的。
5 结论
针对传统摆类动力吸振器抑振频带窄的现状,本文设计了一种具有能量回收功能的自参数摆动力吸振器,研究了该非线性振动系统的动力学特性,并通过数值分析获取了各设计参数对系统抑振性能和俘能性能的影响规律,得到了以下结论:
(1)通过设置自参数摆及附加结构强磁铁,应用封闭线圈来代替摆结构,有效地减小了主质量块的振动幅值,拓宽了动力吸振器的抑振频带,解决了传统摆动力吸振器频带窄的问题,而且还实现了振动能量的回收。
(2)应用简化的频带表达式对比了不同情况下主质量块的幅频曲线,发现在参数f较大或λ1较小时抑振频带变宽,但这两个参数值不会影响到主质量块的振动幅值。当参数q1和ω2较大时,主质量块的振动幅值变小,抑振频带变宽,收集功率也变大。特别是当参数q1与ω2的关系为-ω2=q1时,系统的抑振频带最宽。
(3)参数λ1,λ2,q1和ω2决定着系统的抑振性能和俘能性能。通过改变系统的设计参数,如较小的机械阻尼c1,c2,弹簧刚度k1和摆长l,或增加附加磁铁的磁力有利于提高该吸振器的工作性能。