基于时域残余力向量特征分解的结构损伤识别方法研究
曹震雄,翁 顺,李佳靖,陈志丹,于 虹,闫俊锋,余兴胜
(1.华中科技大学土木与水利工程学院,湖北 武汉 430074;2.中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
引言
残余力向量是将结构损伤状态下的模态数据代入到结构未损伤状态下的特征方程中所产生的误差。残余力向量法是一种基于结构动力学特性的损伤识别方法,结构的动力学特性会随其物理参数(质量、刚度和阻尼)变化,故而由此构建的损伤识别指标能够用于诊断结构的损伤。残余力向量作为一种损伤识别指标有着概念明确、计算简单的优点,能够反映结构的整体和局部信息,因此得到了国内外学者的关注,取得了许多研究成果。
Zimmerman 等[1]提出了一种名为子空间转角法的损伤检测算法,用于分析结构损伤的位置和程度,后来该算法被称为残余力向量法。将该方法用于弹簧模型和二维桁架的试验中,成功地检测出了损伤,但该方法易受噪声的影响。周先雁等[2]将残余力向量法与灵敏度分析相结合,实现对结构损伤的识别。Fukunaga 等[3]通过计算结构的残余力向量确定损伤的大致位置,依据残余力向量误差最小化确定实际损伤位置并得到结构的损伤程度,通过对堆成叠合板结构的数值模拟,验证了该方法的有效性,不过其识别结果受有限元模型精度和测量数据噪声的影响。Ge 等[4]在使用残余力向量定位损伤的基础上,采用矩阵凝聚方法和比例损伤模型,通过计算结构损伤前后刚度和质量特性的变化来量化损伤。Amiri 等[5]使用对角化方法优化模态残余力向量,以避免该方法对框架中间层损伤情况的误判。何伟等[6]针对测试模态信息不完备的情况以及自由度缩聚带来的误差影响,提出了一种改进的残余力向量法,将损伤前后结构同阶的残余力向量差值作为新的损伤指标进行损伤识别,并用简支梁模型数值模拟验证了该方法的有效性以及良好的抗噪性。Behtani 等[7]将残余力向量法应用到复合材料层状梁结构的损伤识别,并用石墨/环氧复合梁的数值模拟验证了该方法的有效性。Wu 等[8]提出了一种实用的残余力分解方法来识别网壳结构的损伤。张干等[9]将残余力向量法应用到高桩码头基桩的损伤识别中,并将残余力绝对值作为损伤指标,拓宽了残余力向量法的应用范围。
传统的残余力向量法都是依据模态参数,通过计算残余力向量判断损伤位置。在此基础上,于德介等[10]结合神经网络方法,将结构残余力向量作为网络的输入,使用正交空间格点法对网络的训练样本进行预处理,解决了训练样本在数据空间分布不均匀的问题,从而提高识别精度和收敛速度。袁颖等[11]将残余力向量法与改进的遗传算法相结合,基于常规模态分析,将结点的残余力向量构造成遗传算法目标函数,在噪声条件下利用改进的遗传算法进行结构损伤定位和定量研究。Yun 等[12]提出一种将残余力向量的灵敏度用于子集选择过程的损伤检测方法,首先进行一个子集选择过程来识别最可能损坏的单元,然后采用稳态遗传算法进行优化以获取与损伤单元相关联的参数的值,在识别多损伤工况时表现良好。Saberi[13]将残余力向量法与电荷系统搜索算法结合,实现对结构损伤的识别。赵一霖等[14]将残余力向量法与树种算法结合,通过残余力向量法找出结构的疑似损伤单元,再利用改进的树种算法反演和识别损伤程度,简支梁数值模拟结果表明该方法有较高的求解精度和较好的鲁棒性。上述文献中使用的方法皆基于动态测试的模态参数,可统称为模态残余力向量,该方法概念明确,相关理论较为成熟,但是测试数据需要进行模态分析等时频变换,且该方法对局部损伤不敏感,不含与损伤相关的时间信息。
杨秋伟等[15]提出了一种静力残余力向量法,利用静力测试位移数据来进行损伤评估,精度更高且更易实现,并进一步提出了静力缩聚残余力向量法,使该方法的应用范围更广,通过对桁架和梁结构模型的数值模拟验证了该方法的有效性。但该方法不含与损伤相关的时间信息,且实际工程中难以施加较大静力荷载。与模态参数相比,动力响应数据能够直接测得,不需进行模态分析等复杂操作,相较于静力测试数据更加容易采集。
因此,本文基于动力响应数据,推导强迫振动下时域残余力向量的计算公式,根据其值在时间上的变化确定损伤时刻;根据时域残余力向量的定义,使用其变异系数构建损伤位置指标,判定损伤发生的位置;在此基础上,对结构刚度变化矩阵进行特征分解,定义了损伤程度参数,以此识别结构的损伤程度。利用时域残余力向量法对武汉军山大桥模型进行损伤识别,数值算例表明,该方法能准确识别损伤的时间、位置和程度,且计算过程简单,无需繁琐的时频变换和迭代运算,具备较好的噪声鲁棒性。
1 时域残余力向量法
1.1 时域残余力向量
对于一个多自由度的线性体系,其结构动力平衡方程为:
式中M,C和K分别为结构的质量、阻尼和刚度矩阵;F(t)为外荷载;x(t),(t)和(t)分别为结构的位移、速度和加速度响应。
一般认为结构发生损伤时刚度发生改变,质量不改变,则有如下关系:
式中Mu,Ku分别为未损结构的质量和刚度矩阵;Md,Kd分别为损伤结构的质量和刚度矩阵;ΔK为结构发生损伤前后刚度矩阵的变化。
由式(1)和(2)可得损伤结构的动力平衡方程为:
将式(3)进行变量分离可得:
式(4)左边含有参量ΔK和x(t)所组成的项以及外加荷载项,其中ΔK是与损伤相关的未知量。式(4)右边由参量Mu,C,Ku和动力响应x(t),(t),(t)所组成,其中Mu,C和Ku是已知参量,动力响应可以通过传感器测得,故通过求解式(4)可识别结构损伤状况。
定义结构的时域残余力向量(Time Domain Residual Force Vector,TRF)为:
通过前面的分析可知,时域残余力向量是将结构损伤状态下的动力响应代入到结构未损伤状态下的动力平衡方程所产生的误差,故而可以通过结构损伤前的物理参数和损伤后的动力响应求得结构的时域残余力向量。
由式(5)可知,当结构没有损伤时,ΔK=0,此时时域残余力向量也为零。结构发生损伤后,ΔK≠0,此时时域残余力向量不为零,且其值与结构的损伤程度相关。因此,可以通过时域残余力向量的突变点判断损伤发生的时刻。
1.2 损伤定位
矩阵TRF中的非零行与损伤位置相关,考虑到模型误差与噪声的影响,TRF中元素离散程度较大的行表明了潜在的损伤位置,为排除结构不同位置结点数据尺度差异的影响,取各结点自由度TRF的变异系数作为损伤定位的指标。实际工程中遇到的噪声多为高斯白噪声,其均值和方差为常数,而噪声影响下未损伤单元相关结点的TRF主要由噪声引起,故而未损伤单元相关结点自由度的TRF变异系数相近,可以通过减去损伤无关结点自由度的TRF变异系数来避免噪声可能造成的损伤位置的误判。为降低噪声影响,定义结构损伤位置指标为:
式中d为自由度编号;σd为d自由度对应的时域残余力向量的标准差;μd为d自由度对应的时域残余力向量的平均值;median(σ/μ)为各结点自由度对应的时域残余力向量的变异系数的中位数。由时域残余力向量的性质可知,损伤位置对应自由度的Loc值会远大于其他位置的Loc值。
1.3 损伤定量
为了确定结构损伤的程度,通过矩阵分解技术[16],对时域残余力向量中的ΔK进行分解,从中提取出刚度损伤参数,即为损伤程度参数,以此来衡量结构的损伤程度。
整体刚度矩阵为单元刚度矩阵经过转换后的叠加:
式中Ti为将局部坐标下n×n单元刚度矩阵转换为整体坐标下与自由度对应的m×m单元刚度矩阵的变换矩阵;n为单元自由度个数;m为结构整体自由度个数;Ki表示第i个单元的刚度矩阵;N为结构的单元个数。
对单元刚度矩阵Ki进行特征值分解,得到:
式中ui为第i个单元的n×r特征向量矩阵;pi为第i个单元的非零特征值{p}i的对角矩阵;r为矩阵的秩。
以一个12 自由度的梁单元为例,可以得到其非零特征值和相应特征向量分别为:
式中E为单元的弹性模量;A为单元的截面面积;G为剪切模量;Izz和Iyy为截面 惯性矩;L为单元长度。
由式(9)和(10)可知,采用式(8)特征分解后,梁单元刚度矩阵特征向量只与单元长度相关,而一般认为损伤前后单元长度不发生改变,因此单元特征向量矩阵在损伤前后不发生改变,而单元刚度非零特征值则与弹性模量和剪切模量相关,即为刚度参数。
整体刚度矩阵可写为:
定义连接矩阵:
进一步整体刚度矩阵可表示为:
式中P为各单元刚度矩阵非零特征值{P}的对角矩阵,{P}为:
若各单元刚度参数的折减程度为αi,则损伤前后的单元刚度参数有如下关系:
将式(16)代入式(13)中,可得如下关系式:
将式(17)代入式(2)中,可得:
则时域残余力向量TRF的表达式可写为:
式(20)中只有一个未知量α,对上式方程两边进行变换可得:
式中A+为A的广义逆矩阵,可通过下式求解:
为了方便求解,定义参数:
则式(21)可写作:
将矩阵展开,可得:
由上述分析可知,结构动力响应是测试数据,则γi和χi都可以通过式(23)计算得到。用单元对应刚度参数的减少评估单元损伤程度,其表达式为:
式中αi即为单元损伤程度参数,其值为单元损伤程度,下标i表示单元刚度参数编号。当某单元损伤程度参数为0,说明损伤前后该单元刚度参数相同,即单元未发生损伤;当损伤程度参数为1,说明该单元损伤后刚度参数为0,即完全损坏。
2 数值试验
2.1 武汉军山大桥算例
将上述基于时域残余力向量的损伤识别方法应用于武汉军山大桥模型的损伤识别。军山大桥全长4881.178 m,桥梁长2847 m,引道长2034 m。军山大桥包括主桥、过渡孔桥、引桥、引道等部分,是一座五跨连续半漂浮体系双塔双索面钢箱梁斜拉桥。主桥长为964 m(48 m+204 m+460 m+204 m+48 m),主梁连续长度为964 m,宽为38.8 m,过渡孔桥主孔跨径为56 m,引桥跨径均为30 m。桥梁全景图及有限元模型如图1 所示。
根据施工图纸建立该工程结构有限元模型,包含758 个单元、611 个结点、3634 个自由度,模型总质量为2.16×109kg。整个模型的单元类型共有“BEAM4”和“LINK8”两种,其中与拉索对应的451~594 号单元采用“LINK8”单元,单元结点有x,y,z三个方向的平动自由度。与索塔对应的1~284号单元和747~758 号单元采用“BEAM4”单元、与主梁对应的285~450 号单元、595~746 号单元均采用“BEAM4”单元,单元结点有x,y,z三个方向的平动自由度和绕x轴、y轴、z轴的转动自由度。以单元刚度折减模拟结构的损伤,为模拟该方法在结构受到单点激励和多点激励下的表现,外荷载分别采用简谐荷载和地震荷载两种。设置不同损伤位置、损伤程度的9 种损伤工况,工况设置如表1 所示。其中,简谐荷载只作用在结构的176 号结点处,为单点激励;地震荷载作用在结构整体上,为多点激励。在简谐荷载和地震荷载两种外荷载作用下,工况1 和4为单损伤工况,工况2 和5 为多损伤工况,工况3 和6为添加10%噪声条件下的多损伤工况,工况7~9 为结构发生较小损伤时的工况。各工况损伤位置如图2 所示,16 号单元为桥墩处的单元,单元两边的结点分别为175 和176 号结点,64 号单元为桥塔处的单元,单元两边的结点分别为184 和185 号结点。各损伤工况中,损伤均设置为第10 s 发生。采用本文提出的时域残余力向量方法,分别对不同工况下的结构损伤进行识别。
在数值试验中,使用高斯白噪声模拟测量噪声,则测量加速度为计算加速度与测量噪声的和[17]:
考虑阻尼影响,以黏滞阻尼理论为基础,根据下式[18]:
由结构固有频率计算出瑞利阻尼系数a0和a1,其中ωm和ωn一般为结构的基频和对结构动力响应贡献显著的高阶频率,ξm和ξn为对应的阻尼比。
本文取结构的第1 阶和第5 阶固有频率进行计算,对应阻尼比均取0.02。
2.2 简谐荷载作用下的损伤识别
模拟简谐荷载作用在军山大桥的176 号结点处(对应桥墩处的16 号单元)。采样频率为200 Hz。施加荷载形式如图3 所示,为两个简谐荷载叠加,如下式所式:

图3 简谐荷载Fig.3 The harmonic load
将Newmark-β 法计算损伤结构的动力响应作为现场试验数据。根据式(5)将损伤结构的动力响应数据代入到未损伤结构的动力平衡方程中,求出结构各结点的时域残余力向量。利用求出的时域残余力向量矩阵计算损伤位置指标,从而确定损伤单元。最后根据式(23)~(26)计算损伤单元对应的损伤程度。
2.2.1 损伤时刻识别结果
由前述对时域残余力向量的分析可知,当结构未发生损伤时,时域残余力向量理论值为0;结构发生损伤后,时域残余力向量非零,考虑到计算误差和测量噪声的影响,可通过分析相关单元结点处时域残余力向量值的变化来判断损伤发生的时刻。以16 号单元对应的176 号结点为例,损伤单元对应结点的时域残余力向量值与时间的关系如图4 所示。
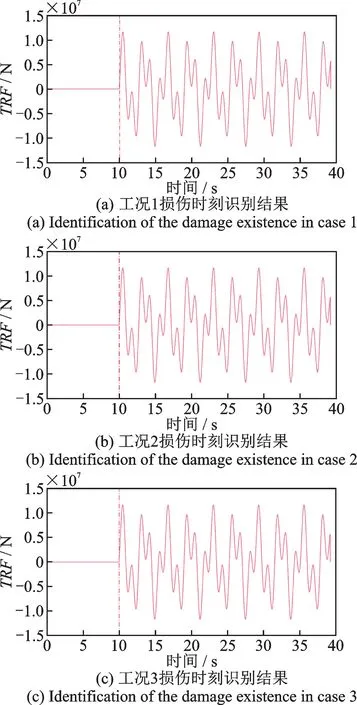
图4 简谐荷载作用下工况1~3 的损伤时刻识别结果Fig.4 Identification of damage existence for cases 1~3 under harmonic loading
图4(a),(b)表明,在不含噪声的工况1 和工况2中,176 号结点的时域残余力向量值在第10 s 之前都约为0,在第10 s 突然增大,并开始变化。由此可以判断两工况下16 号单元损伤的发生时刻皆为第10 s,与预设的损伤时刻相符。图4(c)给出加速度响应含10%测量噪声下的损伤识别结果(工况3),图中176 号结点的残余力向量值自第10 s 开始突变,且此后的值远大于第10 s 之前的残余力向量值,由此可以判断该工况下,损伤时刻为第10 s。综合比较图4(a)~(c)可以得出,简谐荷载作用时,单处损伤、多处损伤以及噪声工况下,模型的损伤时刻都可通过时域残余力向量的突变来识别。
2.2.2 损伤位置与程度识别结果
由时域残余力向量的定义可知,未损伤处结点的时域残余力值会远小于损伤处的时域残余力值。在噪声影响下,未损伤处结点的时域残余力在整个时间段中的变化是相对平稳的,而损伤处结点的时域残余力在损伤时刻则会发生突变。因此用各结点的损伤位置识别指标先确定损伤位置,再计算损伤单元的损伤程度,可以减小矩阵的计算量。各结点的残余力向量在其每个自由度上都存在分量,在识别损伤位置的过程中,只需要选取结点的一个自由度方向上的时域残余力向量计算Loc值来代表此结点即可,这里选取的是y自由度方向上的时域残余力向量。
简谐荷载作用下的3 个工况损伤位置识别结果如图5 所示。
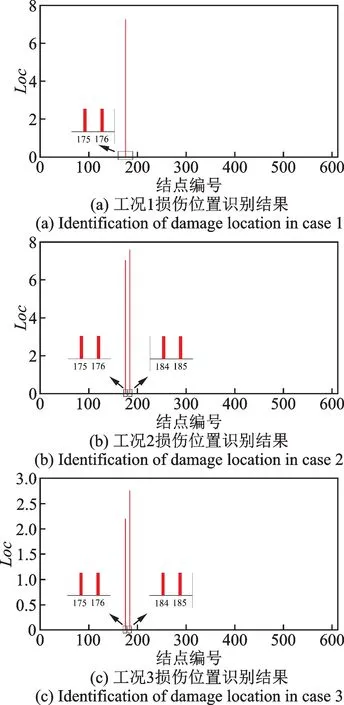
图5 简谐荷载作用下工况1~3 的损伤位置识别结果Fig.5 Identification of damage location in cases 1~3 under harmonic loading
图5(a)表明,175 号与176 号结点的损伤位置指标要远大于其他结点,可知与这两结点相关的16 号单元发生损伤。图5(b),(c)分别是无噪声和有噪声下结构发生多处损伤的工况,两图中175 号、176号和184 号、185 号结点的损伤位置指标都明显大于其他结点,由此可以确定与之相关的16 号单元和64号单元发生损伤。对比图5(b)和(c)发现,在简谐荷载作用下,噪声对损伤位置的识别结果影响不大,该方法在识别结构损伤位置方面具有较强的噪声鲁棒性。
获取了损伤位置之后,根据式(23)~(26)计算损伤单元的损伤程度,得到损伤程度识别结果如图6 所示,表2 给出了各工况损伤程度识别结果的相对误差。
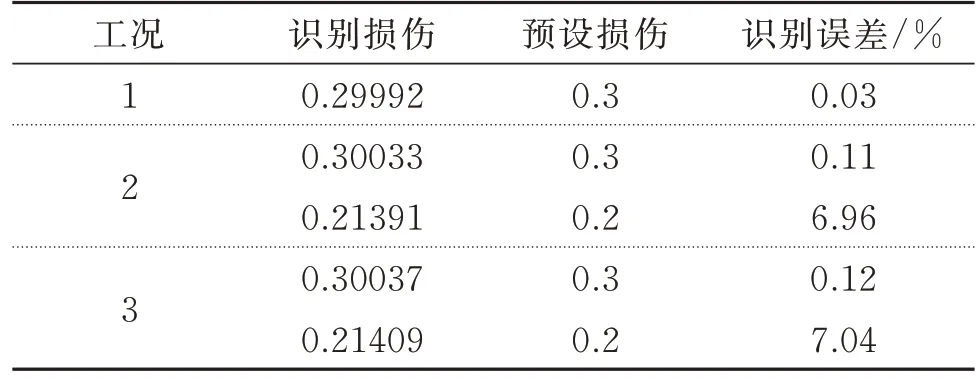
表2 简谐荷载作用下工况1~3 损伤程度识别结果Tab.2 Damage identification results for cases 1~3 under harmonic loading
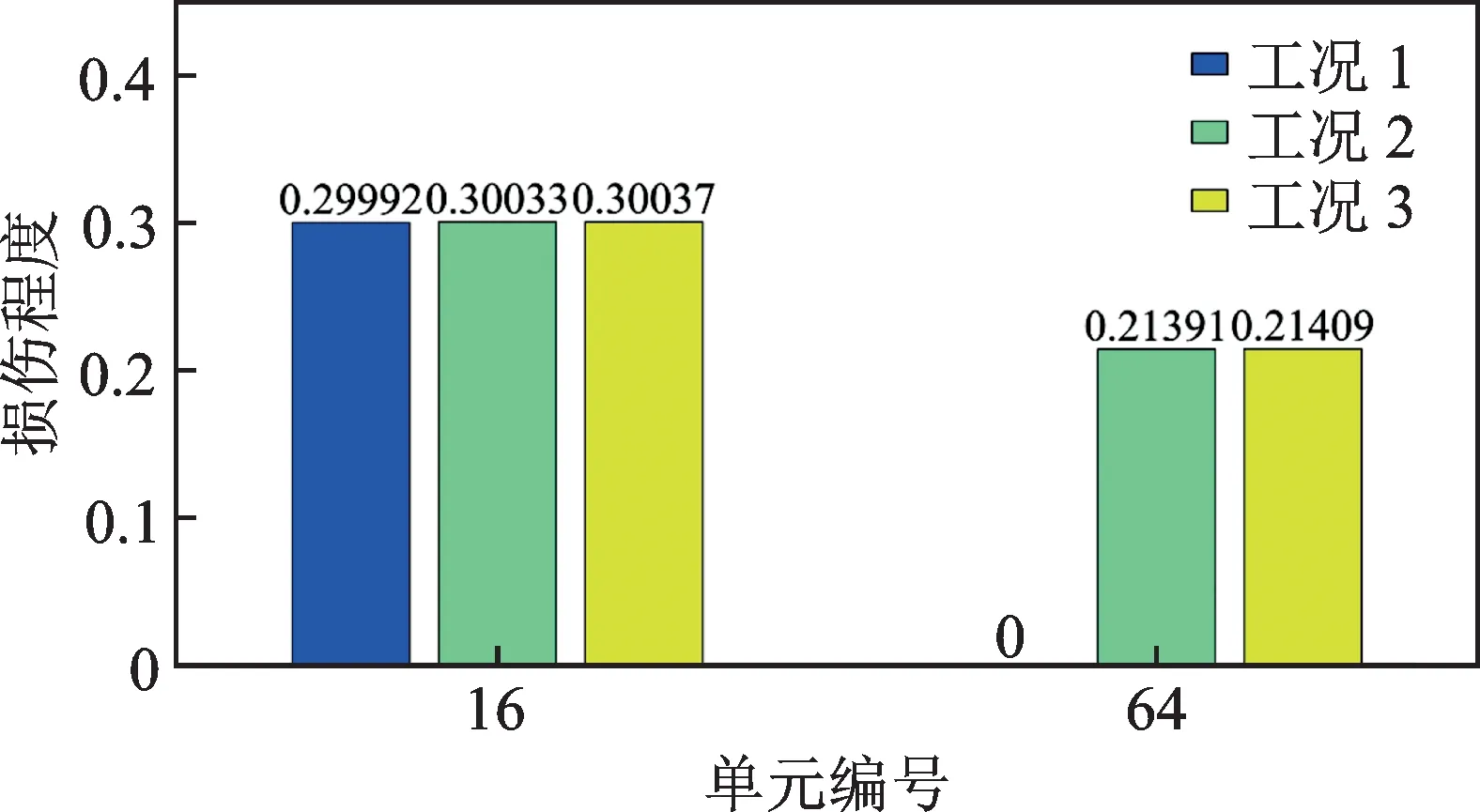
图6 简谐荷载作用下工况1~3 的损伤程度识别结果Fig.6 Damage identification results for cases 1~3 under harmonic loading
由图6 和表2 所示,工况1 简谐荷载作用下,识别出16 号单元损伤,其损伤程度为0.29992,相比于实际设置的损伤程度0.3,误差为0.03%,此单处损伤工况下,损伤程度识别精度较高;工况2 是结构处于简谐荷载作用下,桥墩处的16 号单元和桥塔处的64 号单元发生损伤,两处的损伤程度识别结果分别为0.30033 和0.21391,相对于实际的损伤程度0.3 和0.2,误差分别为0.11%和6.96%;在噪声条件下,两单元的损伤程度识别结果分别为0.30037 和0.21409,误差分别为0.12%和7.04%,相较于不含噪声的工况2 误差略大。因为结构的时域残余力向量矩阵实质上是病态矩阵,对扰动比较敏感,而且当简谐荷载作用在16 号单元时,64 号单元的动力响应较小,容易受到噪声影响,但对比工况2 和3,可以发现噪声对损伤单元的损伤程度识别结果影响较小。
2.3 地震荷载作用下的损伤识别
为了研究时域残余力向量方法在地震荷载下的损伤识别效果,设置了工况4~6。地震荷载采样频率为200 Hz,总的时间步为7851,地震波加速度时程曲线如图7 所示。
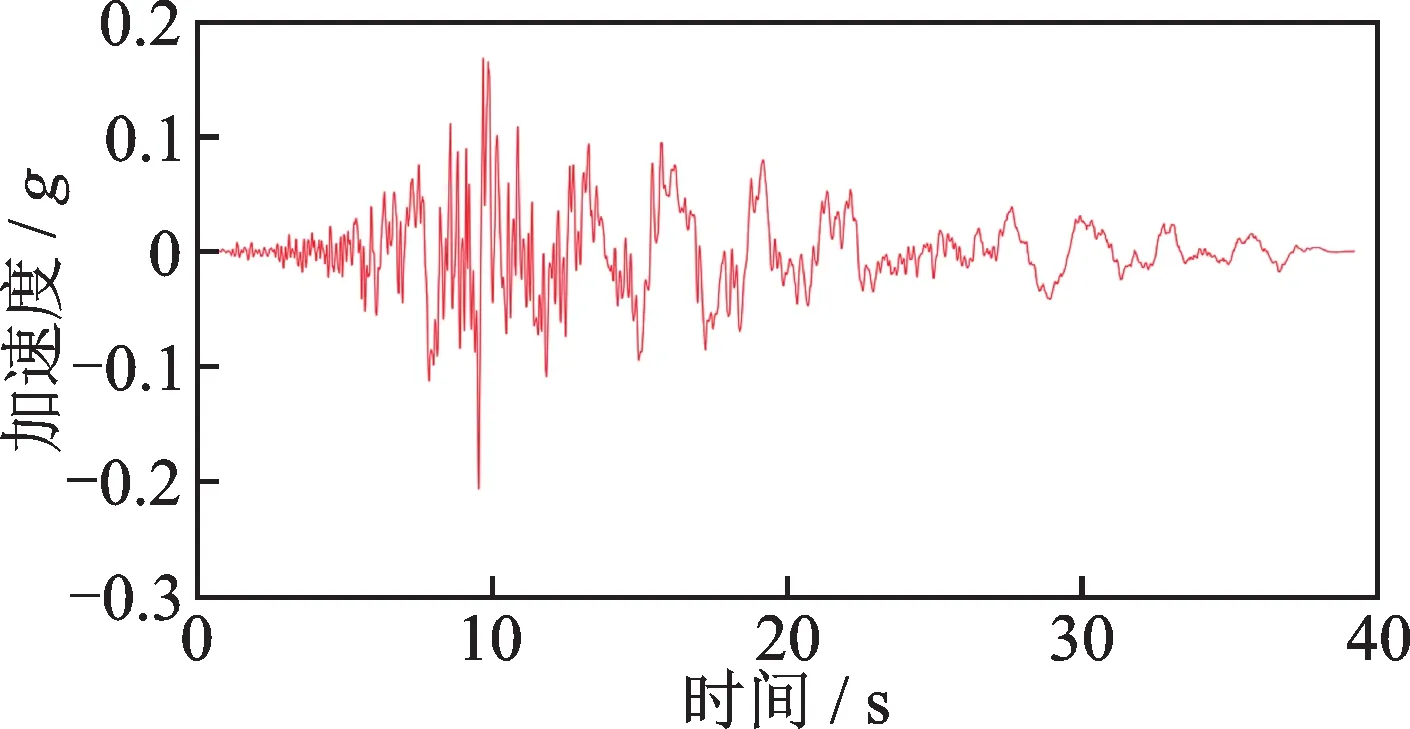
图7 地震波加速度时程曲线Fig.7 Seismic acceleration time history curve
2.3.1 损伤时刻识别结果
计算过程与简谐荷载作用工况类似,同样以176 号结点为例,得到地震荷载作用下工况4~6 的损伤时刻识别结果如图8 所示。
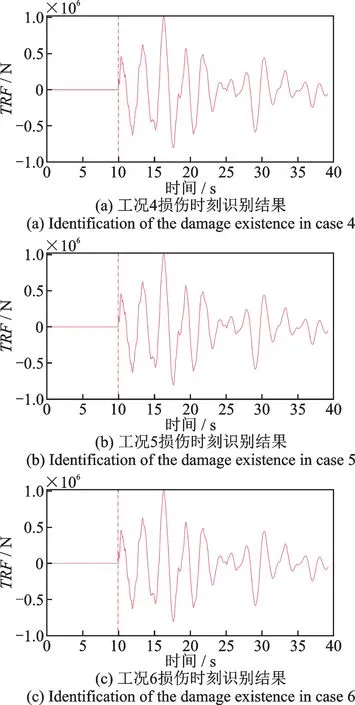
图8 地震荷载作用下工况4~6 损伤时刻识别结果Fig.8 Identification of damage existence for cases 4~6 under seismic loading
图8 表明,在地震作用下的3 个工况中,176 号结点的时域残余力向量皆在第10 s 时突变,与预设的损伤发生时刻相符。比较图8(a),(b)的突变时刻可知,在结构发生单处损伤和两处损伤时,通过时域残余力向量都能较为准确地识别出损伤时刻,结合图8(c)可知,噪声的影响较小。
2.3.2 损伤位置和程度识别结果
类似地,求出结构各结点损伤位置指标如图9所示。图9(a)表明,第175 和176 号结点的损伤位置指标要远大于其他结点,说明与这两结点相关的16 号单元发生了损伤,与预设的单损伤工况的损伤位置相符。图9(b)则证明了在地震荷载作用下,该方法在结构发生多处损伤时的损伤位置识别的有效性。对比分析图9(b)和(c),可以发现噪声对损伤位置的识别影响较小,在加速度含10%水平的测量噪声的情况下,该方法仍能识别出损伤的位置。
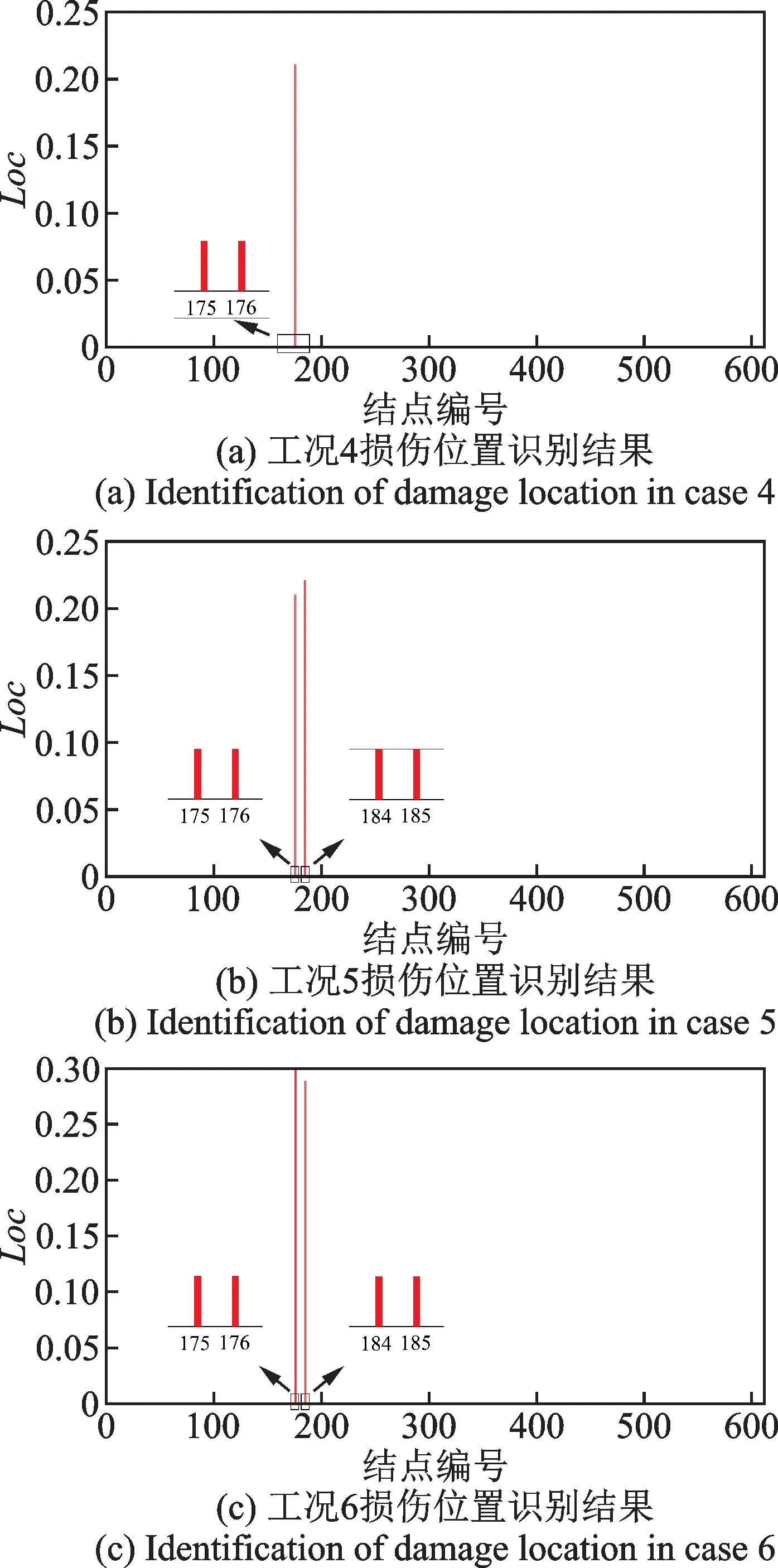
图9 地震荷载作用下工况4~6 损伤位置识别结果Fig.9 Identification of damage location in cases 4~6 under seismic loading
根据上述分析确定的损伤位置,计算损伤单元的损伤程度参数,结果如图10 所示,表3 给出各工况识别结果的相对误差。
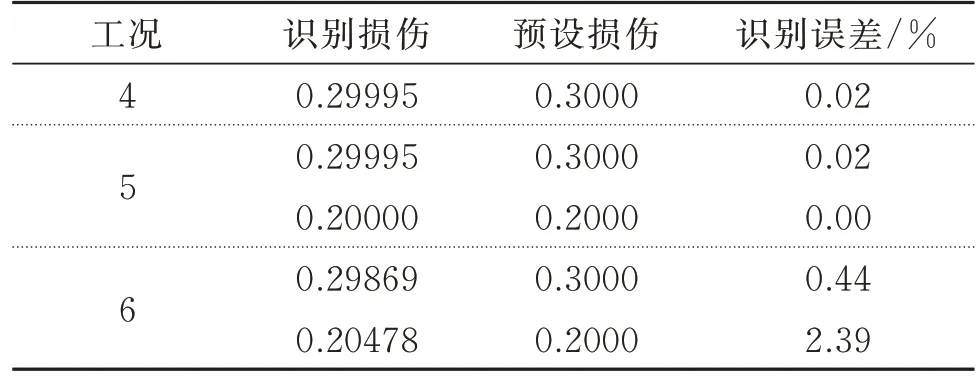
表3 地震荷载作用下工况4~6 损伤程度识别结果Tab.3 Damage identification results for cases 4~6 under seismic loading
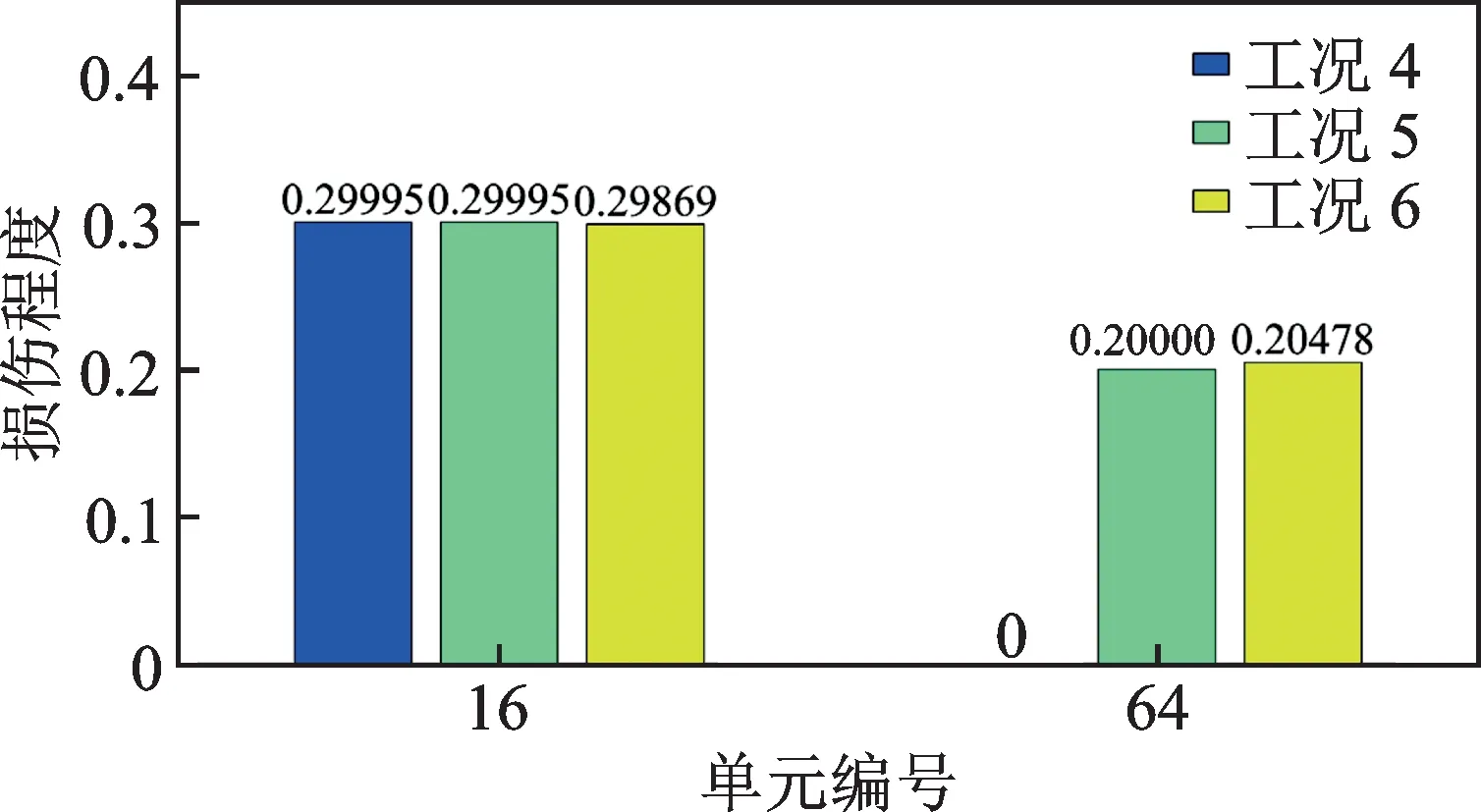
图10 地震荷载作用下工况4~6 损伤程度识别结果Fig.10 Damage identification results for cases 4~6 under seismic loading
如图10 和表3 所示,工况4 地震荷载作用下,识别出16 号单元损伤,其损伤程度为0.29995,相比于实际设置的损伤程度0.3,误差为0.02%,此单处损伤工况下,损伤程度识别误差精度较高;工况5 是结构处于地震荷载作用下,桥墩处的16 号单元和桥塔处的64 号单元发生损伤,两处的损伤程度识别结果分别为0.29995 和0.2000,相对于实际的损伤程度0.3 和0.2,误差分别为0.11%和0.00%,识别结果精度较高;在结构加速度含有噪声的工况下,16 号单元和64 号单元的损伤程度识别结果分别为0.29869和0.20478,误差分别为0.44%和2.39%,相较于无噪声工况误差较大。由表2 可知,简谐荷载作用下的多损伤工况2 和3 的损伤单元64 的损伤程度识别误差分别为6.96%和7.04%,要大于地震荷载作用下的对应工况5 和6 该单元的识别误差,这是因为简谐荷载为单点激励,这种工况下64 号单元的响应较小,损伤识别结果受干扰程度较大,而地震荷载为多点激励,结构整体都受到了作用,误差和噪声的影响较小。结果很好地说明了本文方法在多点激励下的识别效果要好于单点激励。
2.4 小损伤工况下的损伤识别
为了研究时域残余力向量方法在结构所受损伤较小情况下的损伤识别效果,设置了工况7~9。外荷载为地震荷载。
2.4.1 损伤时刻识别结果
以176 号结点为例,由时域残余力向量方法得到地震荷载作用下的小损伤工况7~9 的损伤时刻识别结果,如图11 所示。
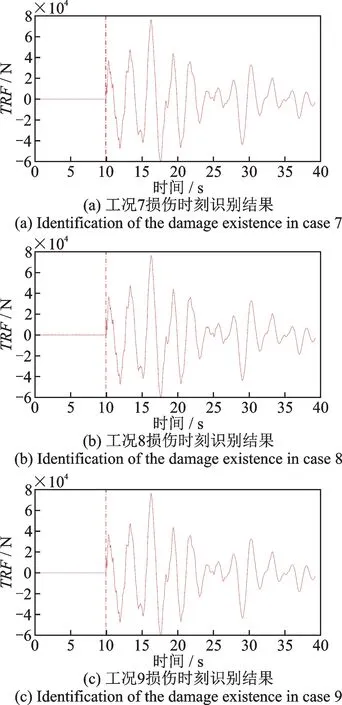
图11 地震荷载作用下工况7~9 损伤时刻识别结果Fig.11 Identification of damage existence for cases 7~9 under seismic loading
图11 表明,在结构发生小损伤的工况下,176 号结点的时域残余力向量皆在第10 s 时发生突变,与预设的损伤时刻相符。比较图11(a)~(c),在结构发生小损伤时,对于不含噪声的工况7 和包含噪声影响的工况8,9,通过时域残余力向量都能较为准确地识别出结构的损伤时刻,噪声对识别损伤时刻的影响较小。
2.4.2 损伤位置和程度识别结果
分别求出小损伤工况7~9 结构各结点损伤位置指标如图12(a)~(c)所示。
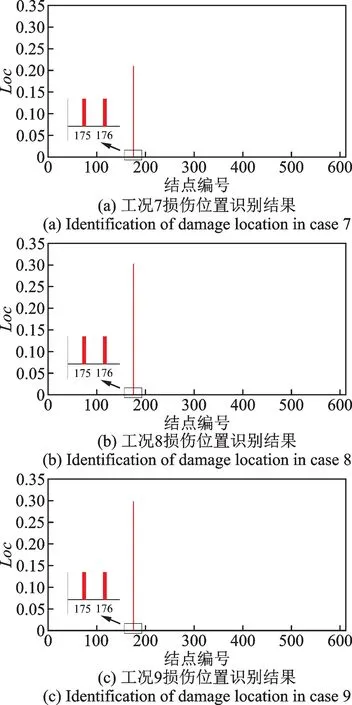
图12 地震荷载作用下工况7~9 损伤位置识别结果Fig.12 Identification of damage location in cases 7~9 under seismic loading
图12(a)表明,175 和176 号结点的损伤位置指标远大于其他结点,说明工况7 下这两个结点对应的16 号单元发生了损伤,与预设的损伤位置相符。工况8 和9 分别在工况7 的基础上添加了10% 和2%水平的测量噪声,对比分析图12(b),(c)和图9(a),可以发现在噪声影响下仍能较为准确地识别出结构发生小损伤时的损伤位置,说明噪声的影响较小。
根据损伤位置的识别结果,可以确定小损伤工况7~9 皆为与175 和176 号结点对应的第16 号单元发生损伤,计算其损伤程度和识别误差如图13 和表4 所示。
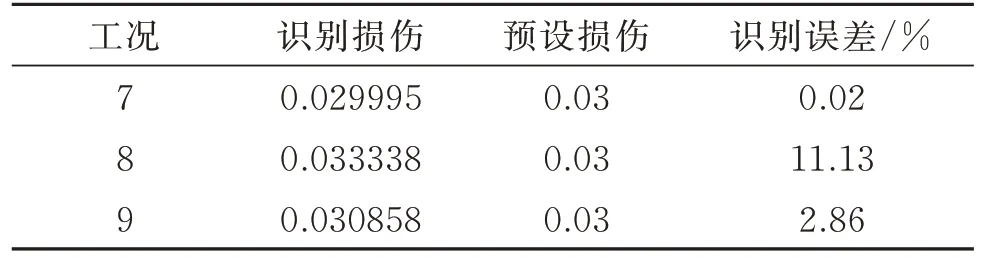
表4 地震荷载作用下工况7~9 损伤程度识别结果Tab.4 Damage identification results for cases 7~9 under seismic loading
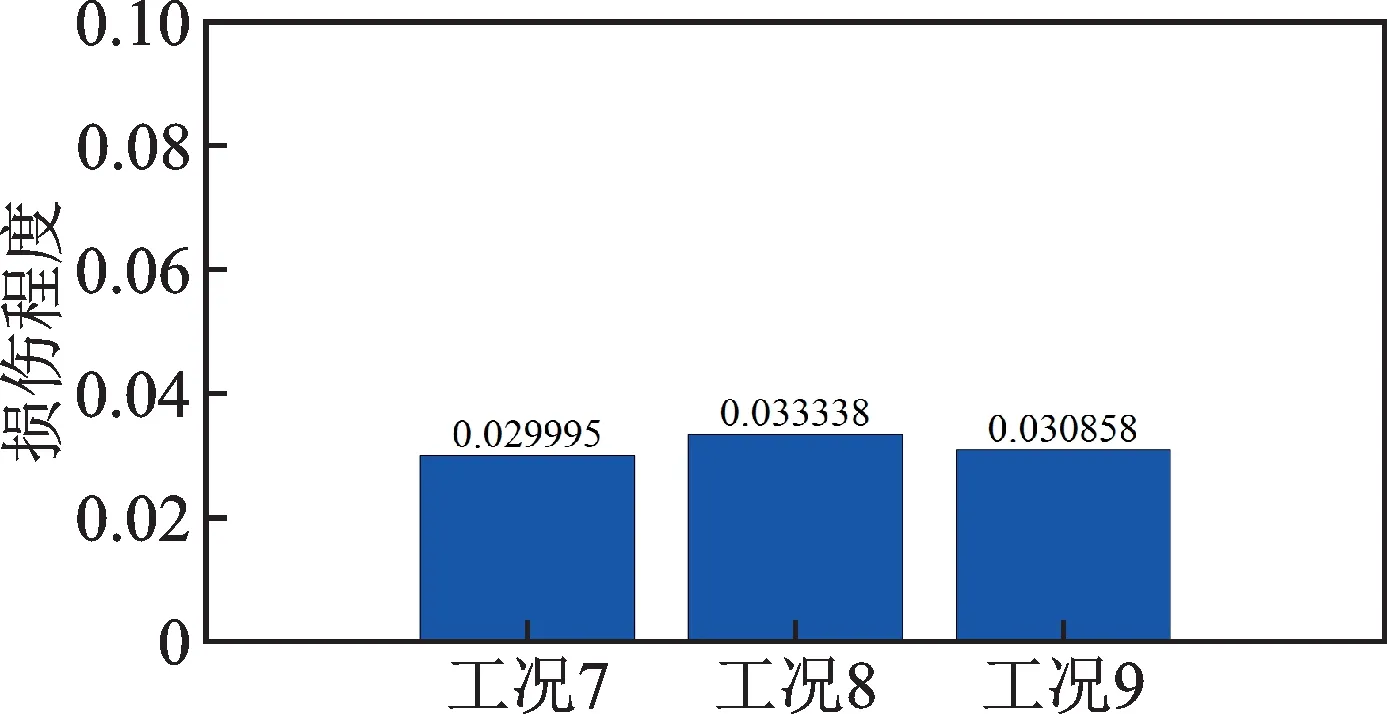
图13 地震荷载作用下工况7~9 损伤程度识别结果Fig.13 Damage identification results for cases 7~9 under seismic loading
由图13 和表4 所示,工况7 识别出结构16 号单元损伤,其损伤程度为0.029995,相比于预设的损伤程度0.03,误差为0.02%。在不含噪声的情况下,可以较为准确地识别出结构发生小损伤时的损伤程度。工况8 在工况7 的基础上在结构加速度响应中添加了10%水平的测量噪声,此工况下识别出16 号单元的损伤程度为0.033338,相较于实际的损伤程度0.03,识别误差为11.13%,此时误差超过10%;工况9 在工况7 的基础上在结构加速度响应中添加了2%水平的测量噪声,此工况下识别出16 号单元的损伤程度为0.030858,识别误差为2.86%,此时误差较小。对比分析工况7~9 的损伤程度识别结果可知,对于结构发生小损伤的工况,其损伤程度的识别结果误差受噪声影响较大,在噪声水平较高时,其识别误差较大,在没有噪声或者噪声水平较低时,仍能较为准确地识别出损伤单元的损伤程度。
3 结论
本文在传统模态残余力向量的基础上,利用时域动力响应数据,推导了强迫振动下时域残余力向量的表达式。根据损伤位置和未损伤位置在时域残余力向量上表现出来的差异,利用结点时域残余力向量值确定损伤时刻,利用其变异系数定义损伤位置指标用来确定损伤位置。在此基础上,进一步推导了刚度矩阵的特征分解公式,由分解公式可知,损伤前后单元刚度矩阵特征向量不发生变化而其非零特征值随损伤程度同步变化,由此可以提取反映损伤程度的单元刚度特征值的变化系数,作为结构的损伤程度参数,用以确定单元损伤的程度。与模态残余力向量法不同,时域残余力向量包含与损伤相关的时间信息,可以通过其判断损伤发生的时刻。将此方法用于武汉军山大桥的损伤识别,识别结果表明:所推导的时域残余力向量可用于单点激励和多点激励下的结构损伤识别,能够准确地识别损伤的发生时刻,定位损伤单元,且能够准确识别单元的损伤程度,具备较强的噪声鲁棒性,多点激励下的损伤识别结果比单点激励下的结果更为准确。目前为保障损伤识别的精度,残余力向量方法需要大量测点的动力响应来计算残余力向量,在之后的研究中,结合动态缩聚[19]、子结构方法[20-21]等有望有效解决测点需求多的难题。