锂离子电池等效电路模型的研究进展

岳永胜,孙 冬*,许 爽,申永鹏

(1. 郑州轻工业大学工程训练中心,河南 郑州 450002; 2. 郑州工程技术学院信息工程学院,河南 郑州 450044;3. 郑州轻工业大学电气信息工程学院,河南 郑州 450002)

锂离子电池已广泛用于电动汽车、智能微电网等领域。确保锂离子电池储能系统安全、可靠和高效运行,需要实时准确预测电池内部状态,如荷电状态(SOC)、健康状态(SOH)和功率状态(SOP)等,因此,电池管理系统(BMS)技术研究显得尤为重要[1]。 为准确描述锂离子电池内外部特性变化,基于模型的电池管理方法得到广泛关注和应用。

常用锂离子电池模型主要有经验公式模型、电化学模型、数据驱动模型和等效电路模型[2]等。 经验公式模型使用一些经验公式来逼近电池非线性特性,是简化的电化学模型,如Shepherd 模型、Unnewehr 模型和Nernst 模型等。 这种模型虽然计算量小,但是精度不高,已逐渐被取代[2]。 电化学模型是从电池内部物理化学过程出发,采用偏微分方程描述多孔电极理论与浓溶液理论的数学模型,通常在实验室中用于模拟电池充放电过程,常见的有伪二维模型(P2D)和单粒子模型(SP),因其依据电化学原理建立,方程复杂、精度较高、计算量大,不适用BMS 实时管理。 数据驱动模型利用黑箱理论、采用机器学习算法,模拟锂离子电池非线性特性,如人工神经网络(NN)、支持向量机(SVM)、模糊逻辑(FL)以及各种复合方法,但过分依赖大量实验数据,实际锂离子电池储能系统运行工况复杂多变,难以获得精度较高的黑箱模型,限制了模型在BMS 中的应用[2]。 等效电路模型采用理想电路元件模拟锂离子电池工作特性,如电阻、电容、电感和可控电压源等,具有线性特性、便于理解、计算容易、实时性较好等优点,成为BMS 技术研究的首选[2]。

1 锂离子电池等效电路模型

等效电路模型不考虑锂离子电池内部化学成分,采用理想电路元件不同组合方式模拟锂离子电池充放电过程和动态特性,具有明确物理意义。 锂离子电池等效电路模型见表1。

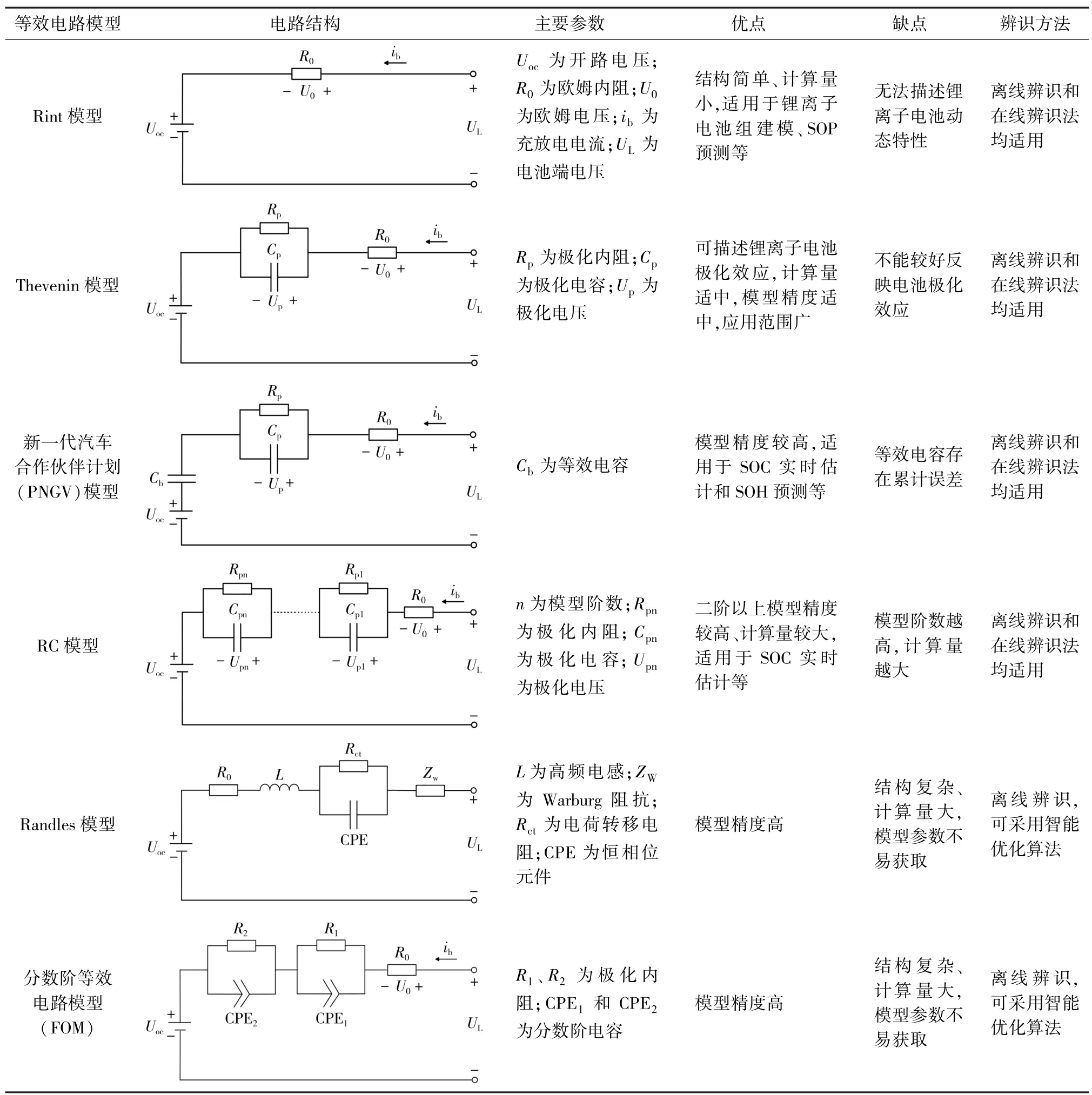
表1 不同等效电路模型对比Table 1 Comparison of different equivalent circuit models

1.1 时域等效电路模型

常见锂离子电池等效电路模型主要在时域范围内模拟电池电气特性,也称为时域等效电路模型,主要包括Rint 模型、Thevenin 模型、新一代汽车合作伙伴计划(PNGV)模型和RC 模型等[3]。

Rint 模型采用随着SOC 的变化而变化的可控电压源Uoc表示电池的OCV。 该模型电路结构简单,由于无法描述锂离子电池充放电过程中浓差极化和活化极化效应,不能精确模拟锂离子电池动态工作状态,电压预测精度较低。 Rint 模型的计算量小、易于功率计算,因此有研究者基于该模型或改进模型,进行锂离子电池组建模和SOP 预测[4]。

Thevenin 模型在Rint 模型的基础上串联了一个RC 并联网络,可描述电池化学反应中的极化效应,适合描述电池充放电过程中动态特性。 该模型电路结构相对简单,计算复杂度较低,比Rint 模型预测电压精度较高,易于工程实现,因此有研究者基于该模型或改进模型,进行电动汽车锂离子电池的SOC 实时估计、故障诊断等[5]。

PNGV 模型源于《PNGV 电池试验手册》[6],相较于Thevenin 模型,增加了模拟OCV 随SOC 变化的电容Cb,可描述电池容量变化。 该模型电路结构复杂度适中,若能准确辨识出电容Cb,模型的电压预测精度会更高,既可用于锂离子电池SOC 估计,又可用于SOH 预测[6]。

RC 模型在Thevenin 模型的基础上串联了n个RC 并联网络,其中n代表该电路模型的阶数。 通过增加RC 并联网络的数量,可提高模型电压预测精度,同时,也加大了模型实现的复杂度[7]。 文献[8]通过实验证明,选择二阶RC 模型或二阶RC 带滞环模型较合适,三阶或三阶以上的RC 模型,精度没有提高反而降低,原因是复杂电路造成了过拟合。

随着模型电路复杂度提高,模型精确度越高,工程实现复杂度和计算量相应增加。 在保证一定模型精度前提下,有研究者提出自适应电路模型,以适应不同负载工况,如不同电路拓扑结构自适应[9]和计算时间自适应[10]等方法。 上述等效电路模型是常见的4 种基本模型,采用线性电路元件描述锂离子电池工作特性,忽略了非线性特性,因此,有研究者针对锂离子电池充放电存在滞回电压的现象,提出带滞环电压的电路模型[10],甚至直接引入非线性环节[11]。

1.2 频域等效电路模型

在频域内,电化学阻抗谱(EIS)是分析、描述锂离子电池电化学特性的主要技术手段,经过EIS 频域数据分析,可建立等效电路模型[12]。

典型锂离子电池的EIS 数据曲线,可分为低频直线段、中频半椭圆段和高频感性段等3 个部分,等效电路模型为Randles 模型。 通常情况下,ZW表示低频段Warburg 阻抗,RC 并联网络表示中频半椭圆段,可描述锂离子电池活化和浓差极化效应,电感L描述高频感性部分,R0表示与实轴相交处的欧姆内阻。 频域等效电路模型采用实测阻抗数据拟合模型参数,能更为准确地描述锂离子电池动态特性,相较于上述常见等效电路模型,模型精度更高[12]。

有研究者在进行模型简化时发现,若采用一系列RC 并联网络代替恒相位元件(CPE)和Warburg 阻抗,整数阶等效电路模型不能准确描述电池动态变化过程,会导致简化模型产生误差[13],因此,提出分数阶等效电路模型(FOM),即采用电容Cpα(0＜α＜1)代替Randles 模型中的CPE 和Warburg阻抗。 分数阶模型能更准确地描述锂离子电池电化学过程,如电荷转移、双电层效应、物质转移和扩散等,在一定程度上提高了模型精度,缓解了在等效电路中串联过多RC 并联网络引起的计算复杂度问题[14]。

2 模型参数辨识方法

选定的电路模型需要匹配适合的模型参数,才能保证模型精确度[15]。 锂离子电池只有充放电电流、端电压和表面工作温度可测量,模型参数需根据这些数据的检测值来进行辨识。 根据在BMS 系统中应用方式的不同,模型参数辨识方法可分为离线辨识和在线辨识。 采用离线辨识方法时,模型参数需提前从实验数据中得到,作为已知参数存储在BMS系统中;采用在线辨识方法时,需要BMS 系统在锂离子电池储能系统正常工作时,实时辨识所需参数并完成建模。

2.1 参数离线辨识方法

离线辨识方法需要配合锂离子电池输入输出数据,从中辨识出模型所需参数。 为使模型可辨识且精确度较高,输入信号必须充分激励锂离子电池所有模态,目前常用的方法有脉冲放电法、脉冲充电法和混合脉冲功率法等。

为使待辨识参数适应不同等效电路模型,有研究者提出采用曲线拟合、最大似然函数(MLE)法、Levenberg-Marquardt算法、最小二乘(LS)法等[3,13,16-17]。 LS 法是一种常用参数辨识方法,通过最小化模型输出和实测数据之间的误差方差,辨识模型参数。

上述离线辨识方法,可得到多组模型参数,为从中选取获得更有效的参数,研究者们提出采用Frisch 函数、赤池信息准则(AIC)等方法衡量建模效果,采用遗传算法(GA)、粒子群(PSO)算法、差分进化(DE)算法和天牛须搜索(BAS)算法等智能算法优化模型参数[13,17-20]。 这些智能优化算法尤其适用于频域等效电路模型参数辨识。

锂离子电池系统呈非线性特性,易受SOC、SOH、环境温度和充放电电流等因素影响,固定的等效电路模型参数无法准确描述工作特性。 有研究者提出用线性变参数(LPV)理论建立电池模型,通过控制调度参数的变化来模拟电池非线性特性,以具有全局稳定性和鲁棒性[21]。

需要在不同影响因素下测试锂离子电池,从而得到各种情况下的辨识数据,获取较准确的模型参数。 文献[22]在不同SOC 状态下,建立变阶RC 模型;文献[23]建立了不同SOC 状态、不同环境温度和不同充电电流倍率下的充电内阻模型;文献[24]建立了不同SOC 状态、不同环境温度和不同电流方向的二阶RC 模型;文献[19]建立了不同SOC 状态、不同环境温度和不同充电电流倍率下带滞回电压的二阶RC模型,并与Rint 模型、PNGV 模型和二阶RC 模型进行对比分析,验证所建模型的优越性。

2.2 参数在线辨识方法

采用离线辨识法所建模型,需要大量锂离子电池测试数据来配合完成,在一定程度上增加了建模成本,不利于实际工程应用,因此,研究者们提出采用在线辨识法,常用辨识算法有递归最小二乘(RLS)法、卡尔曼滤波(KF)法等。

RLS 法通过参数校正和更新,可精确捕捉系统实时特性,实现自适应调节控制跟踪时变参数[9]。 针对RLS 法在线辨识时存在数据饱和、动态运行工况跟踪、数据测量噪声消除等问题,研究者们相继提出采用可变遗忘因子最小二乘(VFFRLS)法、改进带遗忘因子最小二乘(FFRLS)法、偏差补偿最小二乘(BCRLS)法、小波变换VFFRLS 法及遗忘因子多新息最小二乘(FF-MILS)法等算法,用于锂离子电池模型参数在线辨识[25-27]。

KF 法是一种线性最小方差估计方法,可以对含噪声系统的输入输出数据进行最优估计,采用递推方式实现,可用于模型参数的在线辨识。 由于锂离子电池系统呈非线性特性,通常采用扩展卡尔曼滤波(EKF)法、无迹卡尔曼滤波(UKF)法以及改进非线性滤波算法,如自适应扩展卡尔曼滤波(AEKF) 法、自适应无迹卡尔曼滤波(AUKF) 法等算法[15,17,28]。 通常,KF 法与SOC 估计算法联合使用,构成联合卡尔曼滤波法或双卡尔曼滤波法,同时实现锂离子电池模型参数在线辨识和SOC 估计等功能[15]。

2.3 开路电压(OCV)参数获取方法

OCV 是锂离子电池模型的重要参数之一,可直接从实验测试数据中获取,因其与SOC 存在相对稳定的对应关系,最终转化为OCV-SOC 曲线存储起来,作为SOC 估计的重要依据。 由于电池存在极化效应,OCV 参数的获取存在一定的困难,如何快速并准确获得OCV-SOC 曲线,一直是学术界探讨的重要话题。

文献[25]对OCV 测试和参数获取进行详细介绍和分析,将常用OCV 测试方法分为3 种[29-31]:长时间静置法、小电流充放电法和恒流充放电间歇法等。 长时间静置法是通过延长充放电后的静置时间,来减小电池极化电压,使OCV更接近理想电动势,此方法简单、可靠,但测试耗时数十甚至数百小时[29];小电流充放电法即使用C/20、C/25 等小倍率对锂离子电池进行充放电,从而减小极化电压,需耗时数十小时以上[30];恒流充放电间歇法使用标准电流对锂离子电池进行恒流充放电,并保持一定ΔSOC 变化量,再短时间静置,如此循环直至电池充满或达到放电截止电压,需耗时数小时。 文献[25]通过实验测试对比不同OCV 测试方法对锂离子电池建模精确度的影响,验证了采用小ΔSOC 变化量的恒流充放电间歇法,可在保证建模精度基础上,缩短OCV 测试时长;文献[31]为减小长时间静置法测试时长、加快减小极化电压影响,提出一种去极化电流脉冲OCV 测试方法。该方法通过所施加脉冲电流激励,主动消除电池极化效应,可使原测试静置时间由1～4 h 缩短为10 min,从而实现电池端电压快速收敛。

3 结论

本文作者总结和对比了几种常用锂离子电池等效电路模型及参数辨识方法的特点和优缺点。 随着BMS 技术的发展与进步,常见等效电路模型结构相对比较固定,为进一步保证模型精确度,需要研究各种改进的等效电路模型结构及参数辨识方法。 为进一步提高管理技术和功能,将等效电路模型与热模型相结合,用于储能系统热管理等方面,是未来等效电路模型的研究方向。