基于TVFRLS 和SVD-UKF 的锂离子电池SOC 估算

林正廉,卢玉斌,陈 亮,柯彦舜

(1. 福州大学先进制造学院,福建 泉州 362200; 2. 中国科学院福建物质结构研究所泉州装备制造研究中心,福建 泉州 362200)

高效的电池管理系统(BMS)通过监测电池包状态,在保障安全工作的前提下,提高电池利用效率并延缓老化[1]。 荷电状态(SOC)是BMS 监测中的重要状态之一,能够提供电池剩余电量,预测剩余里程数等信息。 准确地估计电池SOC能保障电动汽车运行安全,延长电池寿命。 SOC 无法进行直接测量,只能通过测量电池外部参数进行估计,因此,精确的SOC 估计方法成为BMS 研究中的着重点。

目前,电池SOC 估计方法可大致分为3 类:基于电池物理特性的方法、基于电池模型的方法和基于机器学习的方法等[2]。 基于电池物理特性的SOC 估计方法包括安时积分法与开路电压法,利用SOC 与充放电电流、开路电压的关系,对SOC 进行估算[3]。 基于电池模型的SOC 估计方法,通过构建模型,模拟电池内部动态特性进行SOC 估计,常用方法有粒子滤波、H-infinity、粒子群优化和卡尔曼滤波(KF)算法等,其中,KF 算法通过良好的自校正性能成为在线SOC 估计的首选之一[4]。 基于机器学习的SOC 估计方法有神经网络、模糊逻辑、支持向量机和极限学习机等[5]。 传统KF 算法仅适用于线性系统,因此,有学者提出拓展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)算法[6]。 EKF 算法通过一阶泰勒展开,实现系统的线性化,但只能实现一阶精度,忽略高次项的影响,影响SOC 的估计精度。 UKF 算法通过构建Sigma点,利用无迹转化的方法解决EKF 算法只能实现一阶精度的问题。 在复杂工况下,系统的误差协方差矩阵常常无法保持正定导致算法崩溃,影响了算法的鲁棒性。

针对上述问题,本文作者采用时变遗忘因子递推最小二乘法(TVFRLS)和奇异值无迹卡尔曼滤波(SVD-UKF)联合算法在线估计SOC。 先引入时变遗忘因子,减小由遗忘因子固定导致的辨识精度问题,以提高参数辨识精度,再采用奇异值分解法(SVD),解决传统UKF 算法在复杂工况和计算舍入误差影响下崩溃的问题,以提高鲁棒性与精确性。

1 等效电路模型搭建

1.1 二阶等效电路模型

综合考虑模型的复杂度和准确度,选择二阶RC 模型对电池进行建模。 二阶RC 等效电路模型如图1 所示。

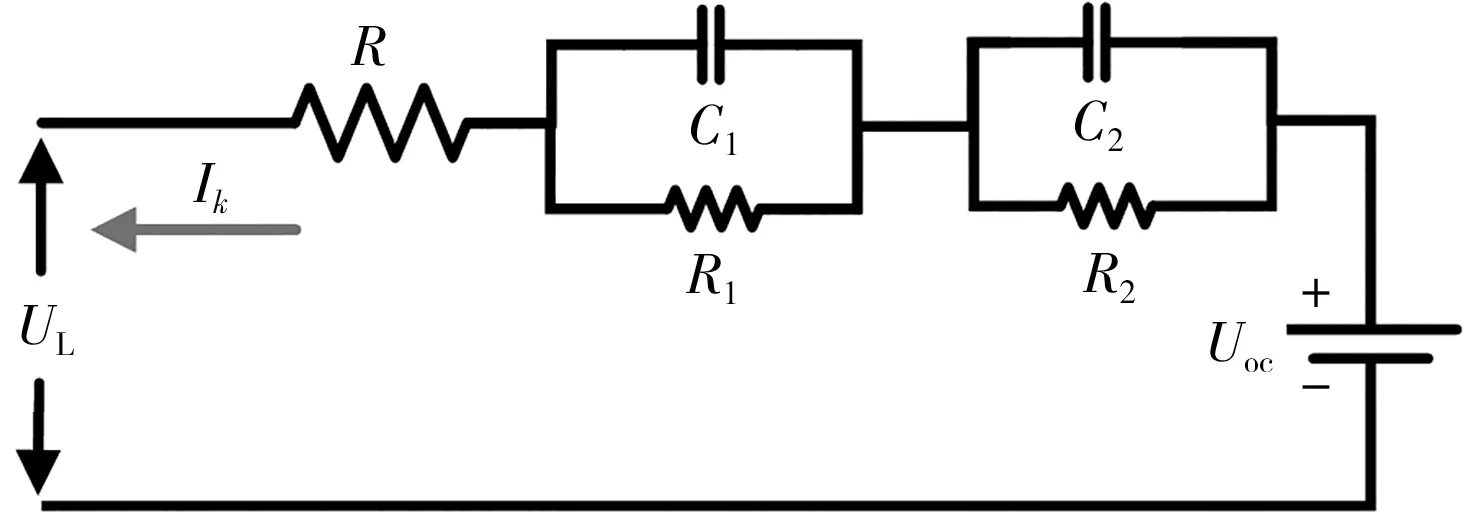
图1 二阶RC 等效电路模型Fig.1 Second-order RC equivalent circuit model

图1 中:Uoc为电池开路电压;UL为电池端电压;R0为电池欧姆内阻;R1、R2为电池极化电阻;C1、C2为电池极化电容;Ik为电流。

为了使二阶RC 电路模型适用于UKF 算法,需要对电池系统模型进行离散化。 选取电池SOC 与两个RC 网络的电压作为系统状态变量、电流Ik作为系统输入变量,结合安时积分法将电池系统离散化。

1.2 基于TVFRLS 的在线参数辨识

在二阶RC 等效电路模型中,开路电压(OCV)与SOC 存在强非线性关系,通过对OCV 和SOC 拟合,可得到OCV-SOC关系曲线。 实验对象为INR18650-30Q 型磷酸铁锂锂离子电池[韩国产,额定电压为3.6 V,充电截止电压为(4.2±0.5) V,放电终止电压为2.5 V]。 实验平台由MP-80PCT-10-20V100A电池测试设备(湖南产)、可编程式恒温箱与上位机等组成。

传统带遗忘因子递推最小二乘法(FRLS)是以残差平方和最小为目标,具体递推方程为:

式(1)中:e(k)为系统预测误差;(k)为当前时刻参数估计值;K(k)为系统增益系数;P(k)为系统协方差矩阵;φ(k)为系统测量矩阵;y(k-1)、φ(k-1)和(k-1)分别为系统前一时刻系统响应、系统测量矩阵和参数矩阵估计值;λ为遗忘因子。

传统FRLS 算法对遗忘因子λ的取值一般为0.95 ～1.00,由仿真实验不断修改λ,取得一个相对合适的值。 在实际动态工况下,使用固定的λ很难较好地适应电池内部复杂的电化学反应,且通过实验法选出的λ较难保证为当前工况下的最优值。 针对以上问题,本文作者引入一种数据开窗理论方法。 通过扩展系统估计误差的数据点个数,对多时刻系统估计误差求均方差,通过均方差大小实时影响λ的取值,从而提高算法的精确性和稳定性。 具体方程为:

式(2)中:M为开窗大小,M=2;H(k)为当前时刻遗忘因子误差系数;ei为i时刻的系统估计误差;λmin为遗忘因子在整个辨识过程中的最小值;λmax为遗忘因子在整个辨识过程中的最大值。

通过城市道路循环(UDDS)测试工况对TVFRLS 算法进行仿真实验,可辨识出二阶RC 等效电路模型的各参数值,辨识结果如图2 所示。 通过分析可以看出,在算法运行初始阶段,由于测试数据量限制导致辨识结果波动较大,随着数据量进一步增大,各辨识参数逐步趋于稳定。

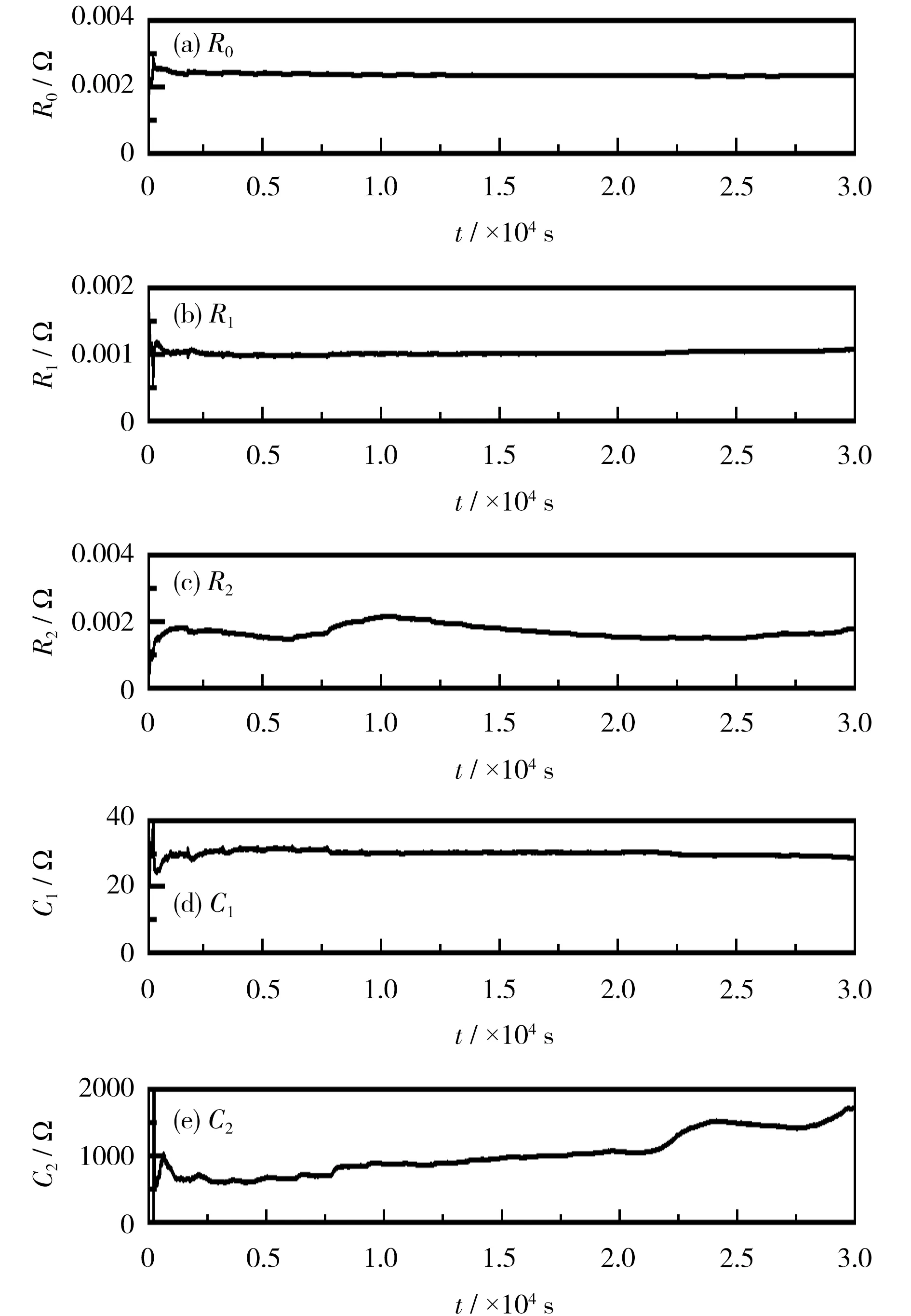
图2 参数辨识结果Fig.2 Parameter identification results

2 锂离子电池SOC 估计

2.1 奇异值分解法(SVD)

使用UKF 算法,对电池进行SOC 估计的过程中,通过无迹变换,避免了求导雅可比矩阵,大幅减小了系统的计算负担。 对比EKF 算法,UKF 算法在无迹变换过程中保留了高阶项,使算法可达到二阶精度。

无迹变换的核心是求协方差矩阵P的平方根;传统无迹转换由Cholesky 变换对协方差矩阵P开方。 具体方程为:

式(3)中:L为下三角实数矩阵。

Cholesky 变换的必要条件是保持矩阵正定,但在实际工况下,协方差矩阵P易受到外部噪声干扰与系统硬件计算导致的舍入误差影响,导致矩阵非正定。 一旦发生上述情况,则无迹转换无法进行,直接导致算法崩溃。 针对该问题,引入SVD 来保持协方差矩阵P正定,提高SOC 估计的鲁棒性。设协方差矩阵为P∈Rm×n(m≥n),R为m×n阶半正定对角矩阵,则该矩阵的奇异值分解为:

式(4)中:U∈Rm×n、Λ∈Rm×n、V∈Rm×n;矩阵U的列向量为矩阵P的左奇异向量;矩阵V的列向量为矩阵P的右奇异向量;S=diag(s1,s2,…,sr)为矩阵P奇异值构成的对角矩阵,r为矩阵P的秩,且s1,s2,…,sr＞0。

2.2 SVD-UKF

UKF 是无迹转换与卡尔曼滤波系统的组合,传统UKF算法采用无迹变换代替泰勒级数展开式,将非线性系统转化为线性系统,提高了算法的精度。 本文作者将无迹变换中的Cholesky 分解用SVD 分解代替,得到SVD-UKF 算法,SVDUKF 算法的其余部分与传统UKF 算法一致。

电池等效电路模型的离散状态方程与测量方程为:

式(5)中:yk为系统响应;f和g为系统状态函数和观测函数;Ak为系统矩阵;Bk为控制输入矩阵;Sock为k时刻系统SOC 值;Uoc(Sock)为k时刻开路电压;U1,k与U2,k为k时刻两个极化回路的电压值;xk=[SockU1,kU2,k]T,为系统的观测变量;wk为系统过程噪声;vk为系统测量噪声。wk、vk均为零均值高斯白噪声,方差分别为Q和R。

具体SVD-UKF 算法估算SOC 流程如下。

式(6)中:E[·]代表均值;x0为初始系统状态变量。

②确定加权系数:

式(7)中:α为比例缩放因子,Sigma 点集的分布状态通过α的取值来确定;κ为缩放参数,决定了采样点的自由度;β为非负权系数,通过β的取值调节高阶项的动差;λf为降低总预测误差的尺度参数;ωm为均值的权重;ωc为方差的权重;n为状态变量的维度。α、κ、β的取值分别为10-4＜α＜1、κ=n-3、β=2。

③使用SVD 法,分解k-1 时刻系统误差协方差矩阵Pk-1,根据分解后的奇异值矩阵生成Sigma 点:

④时间更新,计算向后传播到k时刻系统状态变量均值及误差协方差矩阵预测值:

式(10)中:xk|k-1为基于前一时刻变量值的预测状态变量;xi,k|k-1为k时刻系统状态变量;为k时刻系统状态变量均值的最优估计;Pk|k-1为误差协方差矩阵预测值;Qk-1为k-1 时刻系统过程噪声方差。

式(12)-(13)中:xi,k|k-1与为基于k时刻的观测变量预测值;分别为k时刻误差协方差矩阵的预测值及逆矩阵的预测值;Rk-1为k-1 时刻测量噪声方差。

⑥计算系统增益K,更新状态变量估计值与误差协方差矩阵估计值:

通过不断更新系统状态变量估计值,即可实现SOC 的实时在线估计。

3 仿真实验设计与分析

3.1 实验准备

为了验证TVFRLS 与SVD-UKF 联合算法的估计性能,采用UDDS 工况模拟新能源汽车实际驾驶工况。 通过上位机模拟控制产生UDDS 工况,控制MP-80PCT-10-20V100A 动力电池测试平台对磷酸铁锂锂离子电池进行充放电(电流为-30～10 A,电压为2.5～4.2 V)。 测试平台采集电池模块电压,同时测量充放电电流,随后将测试数据存储,得到UDDS工况下的工作电流与电压,如图3 所示。

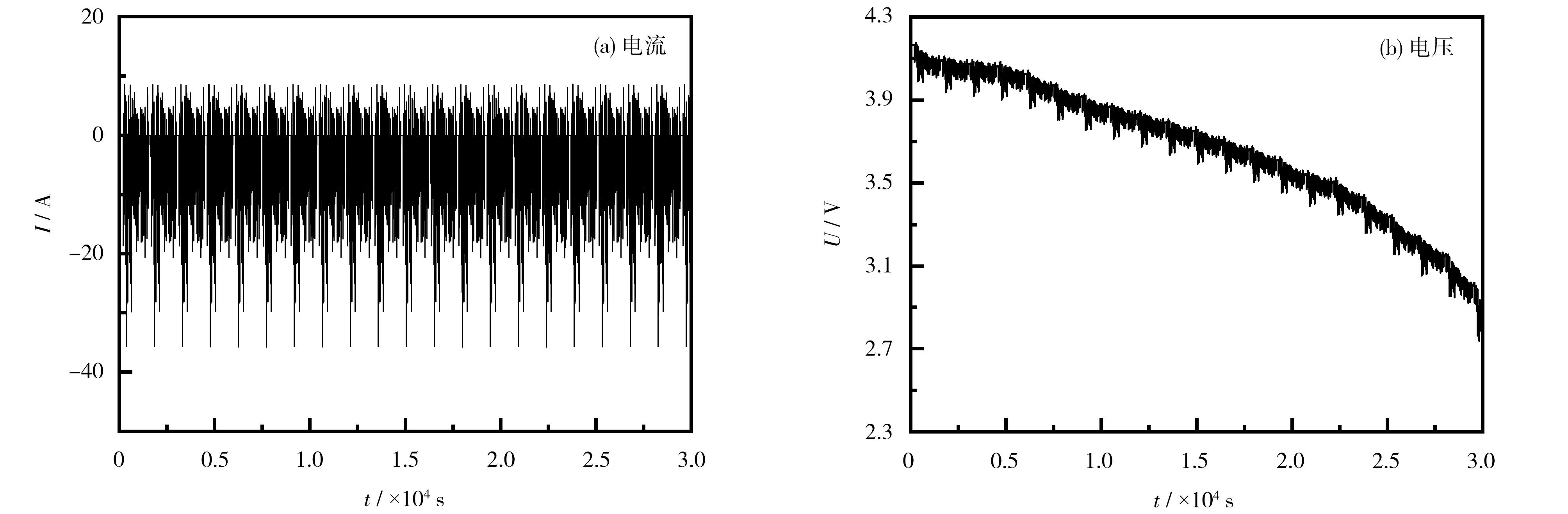
图3 UDDS 工况的工作电流和电压曲线 Fig.3 Working current and voltage curves of urban dynamometer driving schedule(UDDS)

在UDDS 工况下,利用离线参数识别与TVFRLS 辨识算法分别进行仿真实验,可得到两种参数辨识算法的端电压误差。 端电压误差如图4 所示。

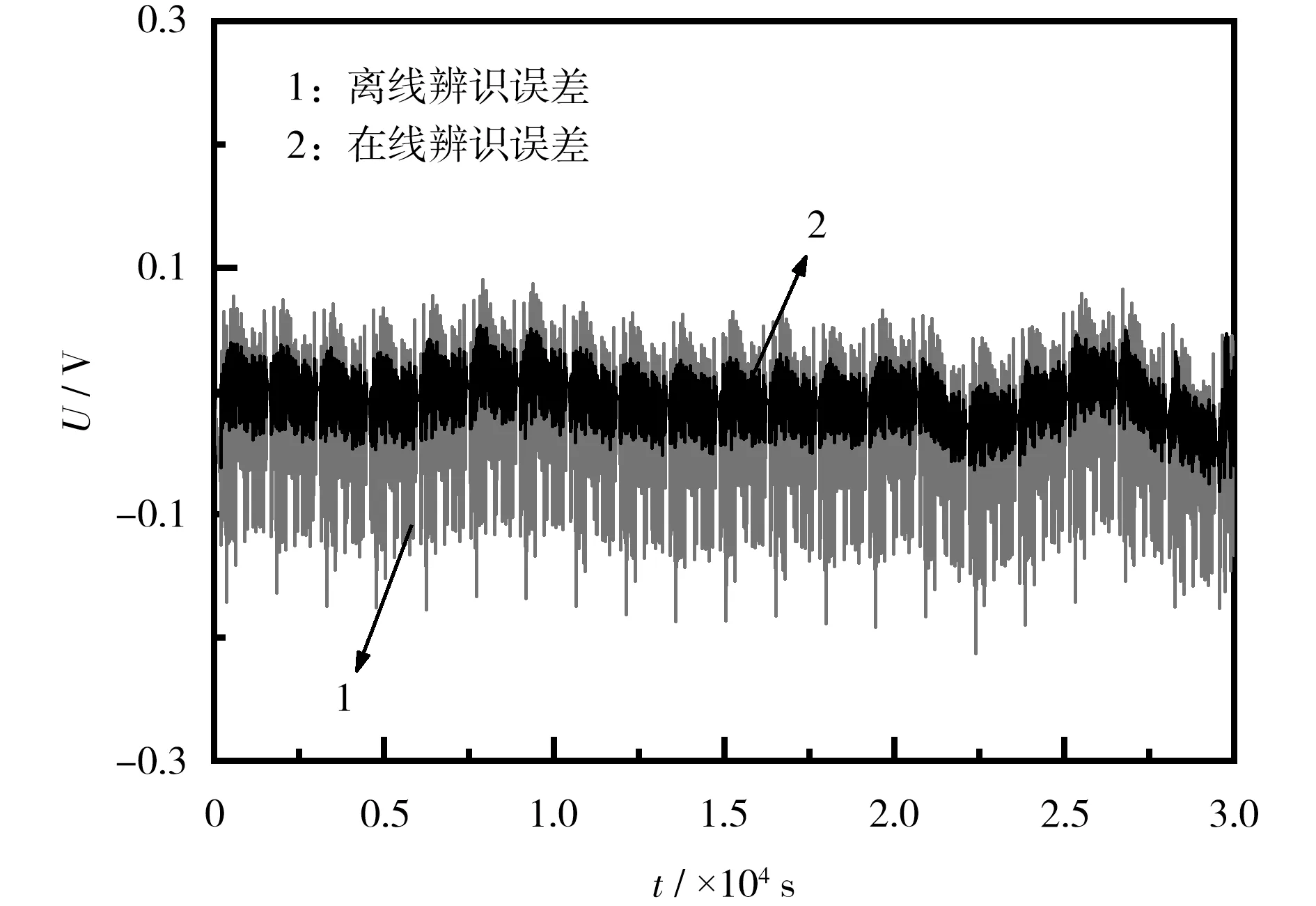
图4 端电压误差Fig.4 Terminal voltage error

从图4 可知,TVFRLS 算法的辨识精度高于离线参数辨识,且平均电压误差为0.011 V。

为了对比联合算法与传统算法的性能,还采用了EKF、UKF 与SVD-UKF 算法进行比较分析。 各算法估计的SOC 结果及各算法与真实SOC 之间的误差见图5。

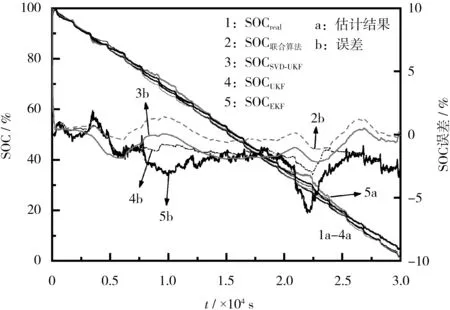
图5 SOC 估计结果及误差Fig.5 Estimation results and errors of state of charge(SOC)

3.2 实验结果分析

从仿真实验结果可以看出,在UDDS 工况下,各算法的SOC 估计值变化趋势基本与真实SOC 值一致。 为了比较4类算法性能之间的优劣,引入最大绝对误差(AEE)、平均绝对误差(MEA)和均方根误差(RMSE)作为性能评判指标,4类算法性能指标对比如表1 所示。

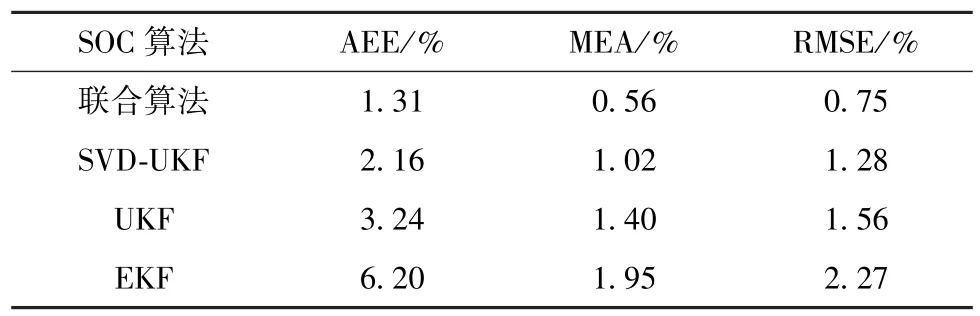
表1 SOC 估计性能指标比较Table 1 Comparison of SOC estimated performance indicators

从表1 可知:首先,SVD-UKF 算法相较于传统EKF 与UKF 算法,AEE 最小,表明对SOC 估计的稳定性要优于传统算法;其次,SVD-UKF 算法的MEA 与RMSE 也小于其余两种传统算法,表明准确性优于传统算法;最后,联合算法在加入了TVFRLS 的前提下,利用SVD-UKF 算法进行在线参数辨识。 联合算法的各项性能指标对比SVD-UKF 算法具有显著提升;估计精度与动态自适应性也全面优于其他传统算法。与传统UKF 算法相比,联合算法的MEA 与RMSE 分别降低了60.0%和51.9%。

为了验证联合算法具有较高的鲁棒性,在SOC 初始值失真且误差协方差初始值P0设置为非正定的情况下,通过UDDS 工况人为设定不同SOC 初始值进行实验。 SOC 初始值的设定分别为0.8、0.6、0.4 和0.2,实验结果如图6 所示。

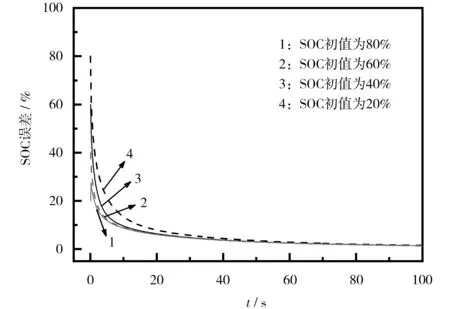
图6 不同初始值SOC 估计误差Fig.6 SOC estimation error of different initial values

从图6 可知,传统UKF 算法无法在误差协方差矩阵初始值非正定的情况下进行SOC 估计,而通过实验可以看出,联合算法不同SOC 初始值在100 s 内均可很好地收敛到真实值附近,说明联合算法在初始值设定产生较大误差时,具有较强的鲁棒性。

4 结论

准确的SOC 估计是实现BMS 各项功能、保证电动汽车安全运行的基础。 本文作者以INR18650-Q 锂离子电池为实验对象,针对传统在线辨识方法遗忘因子固定导致等效电路模型精度低影响SOC 估计的问题,提出基于TVFRLS 以提升模型精度进而提高SOC 估计精度。 此外,还针对传统的UKF 算法在SOC 估计过程中存在误差协方差非正定导致算法失效的问题,提出基于奇异值分解无迹卡尔曼滤波算法,以提高SOC 估计的鲁棒性。 在此基础上,将TVFRLS 与SVD-UKF 进行联合,在提升了SOC 估计鲁棒性的前提下,提高了算法的精确性。 最后,通过UDDS 工况,将联合算法与传统SOC 估计算法进行比较。 通过分析得出以下结论:

在SOC 估计的过程中,联合算法实时更新等效电路模型内部参数,降低了动态工况下由内部复杂电化学反应导致模型参数非线性变化引起的测量误差,提高了估计的精确性。

联合算法通过引入奇异值分解,在初始值失真且误差协方差矩阵非正定的前提下也具有的较强的鲁棒性,从而保证了联合算法进行SOC 估计的稳定性。

联合算法相较于其他传统算法,通过联合TVFRLS 与SOC 估计方法,提高了系统自适应性与SOC 估计精度,在实际应用过程中具有一定的借鉴价值。

联合算法尚未考虑电池在变温环境下的情况,后续算法改进可以由该出发点进行研究。