基于人体适应性的悬浮隧道抑振指标限值研究

杨 孟, 丁 浩, 廖嘉雯, 李 科, 陈建忠

(1.招商局重庆交通科研设计院有限公司, 重庆 400067; 2.公路隧道国家工程研究中心, 重庆 400067)

水中悬浮隧道是一种跨越长大水域的新型交通构筑物,相较传统跨海交通结构,悬浮隧道具有受海底地质影响、自然灾害影响较小以及造价低等特点,已成为未来重要的跨海交通结构[1]。悬浮隧道作为柔性、长线型的交通结构体,在水中受到波流耦合的影响容易产生振动,其振动效果对司乘人员的适应性有较大影响[2-4]。目前悬浮隧道参考海上平台、浮桥以及人行桥等结构振动抑制方法,开展了相关抑振方法、措施的研究,但因悬浮隧道与其他平台结构形式、波流环境、振动模式等参数不同,目前水中悬浮隧道抑振方式与效果对司乘人员适应性却没有统一的标准及描述。因此,如何确定悬浮隧道抑振措施、指标及其限值,才能保障司乘人员的适应性,这是目前悬浮隧道设计中亟待解决的问题。

目前国内外相关规范和专家学者对结构振动下人体适应性评价开展了诸多研究。美国AISC标准中根据不同振幅与频率大小对人体振动感知进行了划分;ISO2631—1:1997标准[5]中提到人体承受的全身振动的评价,研究振动的主要频率在0.5 Hz～80 Hz以上,并根据人体接受加速度制定了接受限值。我国后续的机械、桥梁、道路等相关振动标准基本上参考ISO标准制定。由于不同交通环境的振动特性不同,且均为周围环境与抑振措施共同作用的结果,各学者开展了不同领域的研究。胡启国等[6]为了研究振动对乘坐舒适性的影响,建立了路面-车辆-座椅自由度动力学模型,通过主动控制振动,可有效抑制共振峰值,提高乘坐舒适性;张杰等[7]利用有限元法和动力平衡原理,建立了13个自由度的大型客车人体三维模型,分析了人-车-路耦合振动下车辆和人体的动力响应,研究了俯仰与侧倾加速度对人体适应性影响;王锋等[8]研究了不同摩擦系数、不同平整度、不同速度下的加速度与人体主观感受之间的关系,分析了摩擦系数条件下的平整度、速度和加速度的关系,提出了满足驾乘舒适性的条件下最大行车速度和路面平整度之间的关系;郑木莲等[9]根据车辆通过路桥过渡段时人体承受振动的特点,采用压电式加速度传感器测量车辆通过路桥过渡段时人体承受的竖向加速度,提出了新的人体舒适性评价方法;彭勇等[10]研究了心率变异性与高速列车乘员舒适度之间的关系,开展了高速列车乘员舒适度实车试验,结合主观舒适度问卷反馈结果,分析了驾乘人员的平均心跳间期、心跳间期标准差等特征在舒适度劣化时的变化情况;同时为了解不同人群对同种振动环境下振动的不同感受,部分研究者通过构建标准人体仿真模型,分析了模型在不同振动条件下动力学响应,张鄂等[11]为高效评价振动环境下人-车系统的人体乘坐舒适性,运用ADAMS/View和LifeMOD软件构建了人-车系统生物力学仿真模型,开展了不同路面与不同车速的人体乘坐舒适性仿真研究;张继奎等[12]通过振动台模拟爆破振动开展了人体振动反应试验分析爆破振动参数、心电指标以及人体主观感受的量化关系,构建了爆破振动影响下人体舒适度评价体系;朱前坤等[13]为克服时程分析耗时和占用巨大计算机资源的缺点,自建某钢-玻璃简支梁桥,提出一种基于AISC Design Guide快速评估人行桥人致振动舒适度的频率响应函数方法;杜阳阳等[14]从水平两向振动的影响出发,通过人体动力特性的振动台试验,分析了人体动力响应并建立相应的人体动力学模型,对人体振动舒适度评价问题进行了研究;李著新等[15]通过仿真和试验相结合的方法分析了船舶双层底板架结构的声振响应,提出了邮轮振动噪声舒适度评价标准在评价区域和评价指标2个方面的相关建议。

综上分析,现阶段相关专家学者主要针对陆地、海上平台、轮船等振动特性对人体适应性影响进行了研究,但对水中结构物振动的研究较少。为此,本文通过分析振动状况下人体适应性评价标准,综合相关已有研究成果,提出悬浮隧道人体适应性评价标准,构建悬浮隧道人体有限元仿真模型,分析不同振动特性下人体各部位动力学响应,并根据人体适应性评价标准提取悬浮隧道抑振指标限值,为悬浮隧道实体工程落地设计提供数据支撑。

1 振动特性人体适应性标准研究综述

早期主要通过模拟试验或真实试验对人体加速度和主观感受获取人体适应性标准,进而获取适应性曲线,近年来逐渐增加了人体生理心理指标的测量;适应性判断方法逐渐多元化,除了根据规范阈值进行判断,有部分学者结合试验数据推导相应的舒适度经验公式并得到广泛应用,还有学者结合烦恼率模型及模糊综合评价方法获取更真实全面的适应性评价。另外,也有学者创新性地采用GUI电脑界面模仿振动环境研究人体振动感知能力的变化。

总结各领域人体适应性评价标准研究成果与规范要求,发现不同领域适应性评价的侧重点不同,对应领域振动适应性指标存在显著区别。公路交通与桥梁以ISO 2631-1:1997标准为基础,采用竖向加速度对人体适应性进行分段评价;轨道交通因对车辆运行过程中的平顺性和稳定性要求较高,适应性评价指标阈值主要集中在振动速度和计权加速度2方面;轮船比较大,更注重不同人群(乘客与工作人员)、不同区域的振动适应性;飞机由于航程长短差异较大,会对振动持续时间较为关注;爆破振动重点考虑爆破振动次数、周围区域的用地性质、爆破的时间段等。不同领域的人体适应性评价指标限值也不同,大部分振动计权加速度的阈值主要集中0.1 m/s2～2 m/s2,而飞机、潜艇等设备在升降过程中设备本身会产生较大的短时振动,故不同工况下阈值范围波动较大,飞机z轴方向为0.14 m/s2～28 m/s2,潜艇为1.67 m/s2～8 m/s2。

据此,由于悬浮隧道振动频率受到波流影响较大,而实际波浪周期是动态变化的(通常为0.063 Hz～0.3 Hz),不同周期下人体对加速度的感知存在差异,为满足实际设计需要,结合各领域现有规范及文献研究成果对悬浮隧道的适应性上限阈值展开讨论并给出建议值。

1) 以水平加速度为评判指标

人行桥在ISO给出了行人运动过程中满足振动适应性的临界曲线,适用的频率范围为1 Hz～10 Hz,水平计权加速度限值为0.3 m/s2～0.7 m/s2,随着频率的增加而增大;浮桥在通常暴风雪的工况下,允许的最大水平加速度为0.5 m/s2;海上结构相关规范标准适用频率为0.063 Hz～1 Hz,其水平振动判断指标为水平均方根加速度,见表1;此外半潜式海洋平台在游览情况下(0.01 Hz～0.28 Hz)的水平均方根加速度值为0.294 m/s2。根据上述分析可知,随着结构振动频率的增加,人体可接受水平加速度限值逐渐减小,在0.01 Hz～0.3 Hz的情况下,当水平加速度超过0.20 m/s2时,人体会产生不舒适的感觉。综上相关结构物适应性研究,悬浮隧道在0 Hz～0.3 Hz范围内,水平加速度取值约为0.2 m/s2。

2) 以竖向加速度为评判指标

建筑物主要受竖向振动,楼盖结构自振频率不宜低于4 Hz,其对应竖向振动有效最大加速度限值为0.2 m/s2或0.5 m/s2(不同区域上限值不同);半潜式海洋平台在游览情况下的竖向均方根加速度值为0.196 m/s2;Masashi等对0.01 Hz～1 Hz频率范围内人体振动适应性进行了研究,结果表明,加速度超过0.20 m/s2,人体将产生不舒适的感觉。另外,在0.1 Hz～0.5 Hz时容易导致运动病,现有大量研究表明,运动病与竖向振动存在直接关系,当振动频率固定时,竖向振动加速度越大,呕吐率越高;当振动频率在0.083 Hz～0.2 Hz时,竖向计权振动加速度超过0.278 m/s2会发生呕吐反应。综上,振动频率在0 Hz～0.3 Hz范围内,选取的竖向加速度值约为0.2 m/s2。

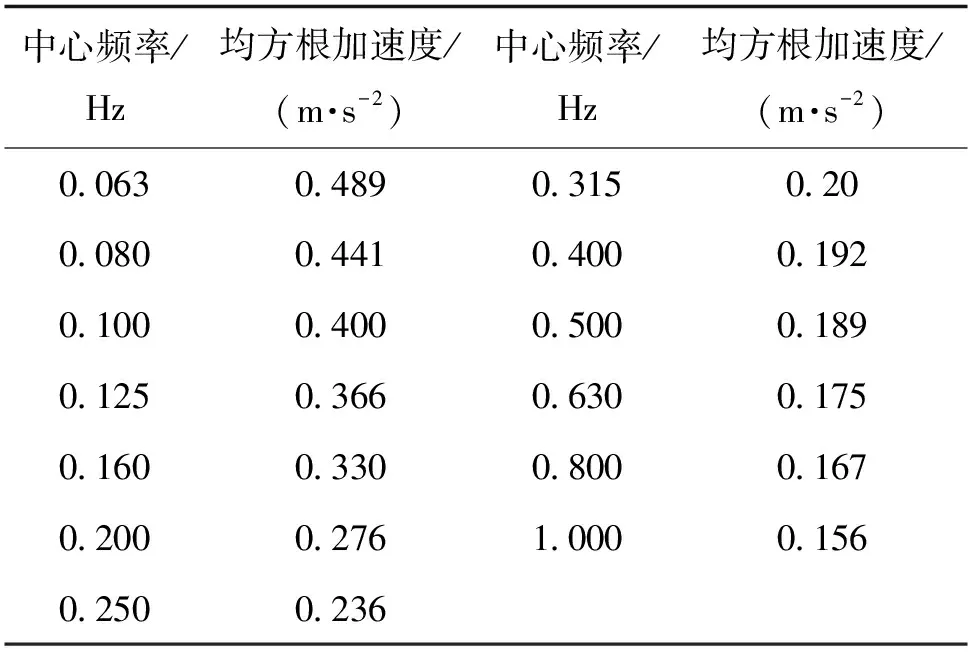
表1 水平振动均方根加速度限值

3) 以计权加速度为评判指标

从计权加速度的角度给出人体适应性评判标准,ISO 2631-1:1997标准主要规定频率范围为0.5 Hz～80 Hz,当计权加速度大于0.315 m/s2时,人体开始感觉到不舒适;船舶标准中在振动频率为1 Hz～80 Hz下,振动特性对人体适应性计权加速度限值为0.214 m/s2,相关研究并没有对振动频率0 Hz～0.5 Hz之间计权加速度进行分析。综合相关研究及规范可知,人体适应性评价加速度主要集中在0.2 m/s2左右。

根据上述分析,初步得到悬浮隧道人体适应性加速度限值为0.2 m/s2,悬浮隧道振动产生的加速度小于0.2 m/s2,该工况下人体没有感觉;一旦加速度超过0.2 m/s2,则人体会产生不适感觉。

2 悬浮隧道立姿人体仿真试验

2.1 悬浮隧道动力学仿真

由于目前世界上并未存在真正的悬浮隧道工程,采用Abaqus构建悬浮隧道结构,设置水中不同参数中悬浮隧道动力学响应,其部分参数设置结果见表2,模拟结果如图1所示。模拟正常工况(4 m波高)与极端工况(8 m波高)下悬浮隧道在未增加抑振措施时跨中段动力学响应,模拟结果见表3。

表2 悬浮隧道模型部分参数

图1 悬浮隧道振动模拟结果

由表3可知,悬浮隧道在未增加任何抑振措施情况下竖向位移与加速度变化相对较小,而水平位移在正常工况下水平加速度已超过了0.2 m/s2,若不采取任何措施,人员在悬浮隧道会存在不适应表现;在极端工况下水平位移已达到了1.3 m,且其加速度接近于1 m/s2,其环境已不能适合人员工作或通行,甚至可能会对悬浮隧道的稳定性产生影响。采用抑振措施可有效降低其加速度,但抑振指标与限值都需进一步研究。

表3 不同工况悬浮隧道振动仿真结果

2.2 立姿人体模型构建

由于人群不同、承受能力不同、感受不同,导致采用人体现场试验的方式对振动产生加速度的研究难以准确判断。随着计算机技术的逐步发展,有限元法成为分析人体力学变化极为有用的工具,通过有限单元、节点、自由度等试验条件控制,其模拟的条件更贴近实际,计算结果的可信度更高。本研究根据人体结构特点,采用有限元模型构建标准人体结构模型,人体模型包括人体的皮肤、肌肉以及骨骼。模拟标准男性人体,年龄为25～29岁,人体身高171 cm,体重59.9 kg,构建的人体模型如图2所示。

2.3 立姿人体振动仿真

通过分析悬浮隧道在波流耦合作用下振动特性响应,提取其位移的时程曲线,并在仿真软件中加载在人体有限元仿真模型中。以振动频率0.1 Hz为例,最大振幅设置由0.01 m逐步增长到1 m,分析人体不同部位加速度的变化。人体在不同振动状态下各部位加速度的值分别如图3所示,其中仿真模型中人体颜色从浅到深分别表示人体所受加速度由小到大。

图2 人体有限元仿真模型

(a) 振幅为0.01 m

(b) 振幅为0.42 m

(c) 振幅为0.78 m

由图3可知,在悬浮隧道振动频率一定的条件下,人体各部位加速度随着振动振幅的增加而不断增大;在人体表面与肌肉受到加速度变化相对于骨骼较小;图3(b)中腹部骨骼的加速度明显高于周围其他骨骼位置;图3(c)与图3(d)中颈部骨骼的加速度明显高于其他位置,表明在悬浮隧道振动条件下,人体颈部与腹部是最易感受到不适应的部位。

同时,分析不同振动工况下人体仿真模型的加速度结果,以振动频率为0.06 Hz为例,不同振幅下人体模型各部位加速度结果如图4、图5所示。从图4可以看出,随着振动振幅的增加,颈部与腹部骨骼受到的加速度均高于人体表面。由图5统计结果可见,在振动条件下,人体腹部骨骼振动变化受加速度影响明显,其均值与众位数均高于人体表面与颈部骨骼。因此,通过人体不同部位在悬浮隧道振动条件下受到加速度结果,以腹部骨骼加速度作为人体不适应性的极限标准。

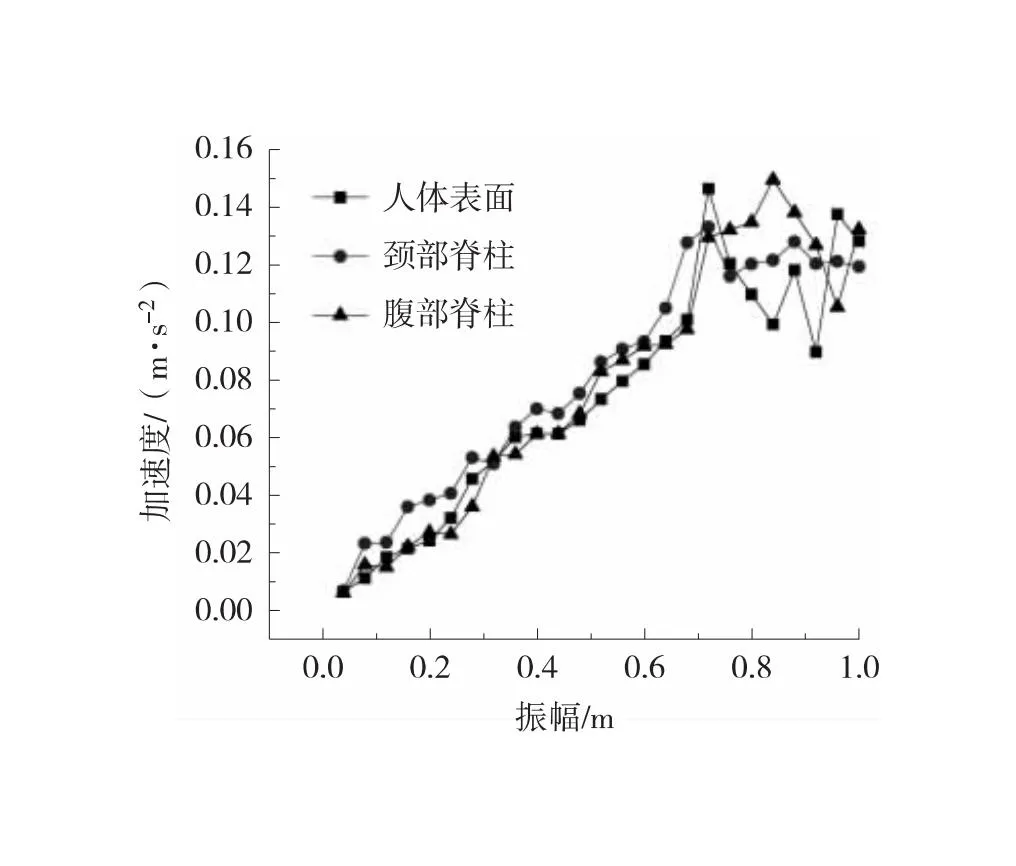
图4 不同振幅下人体模型各部位加速度

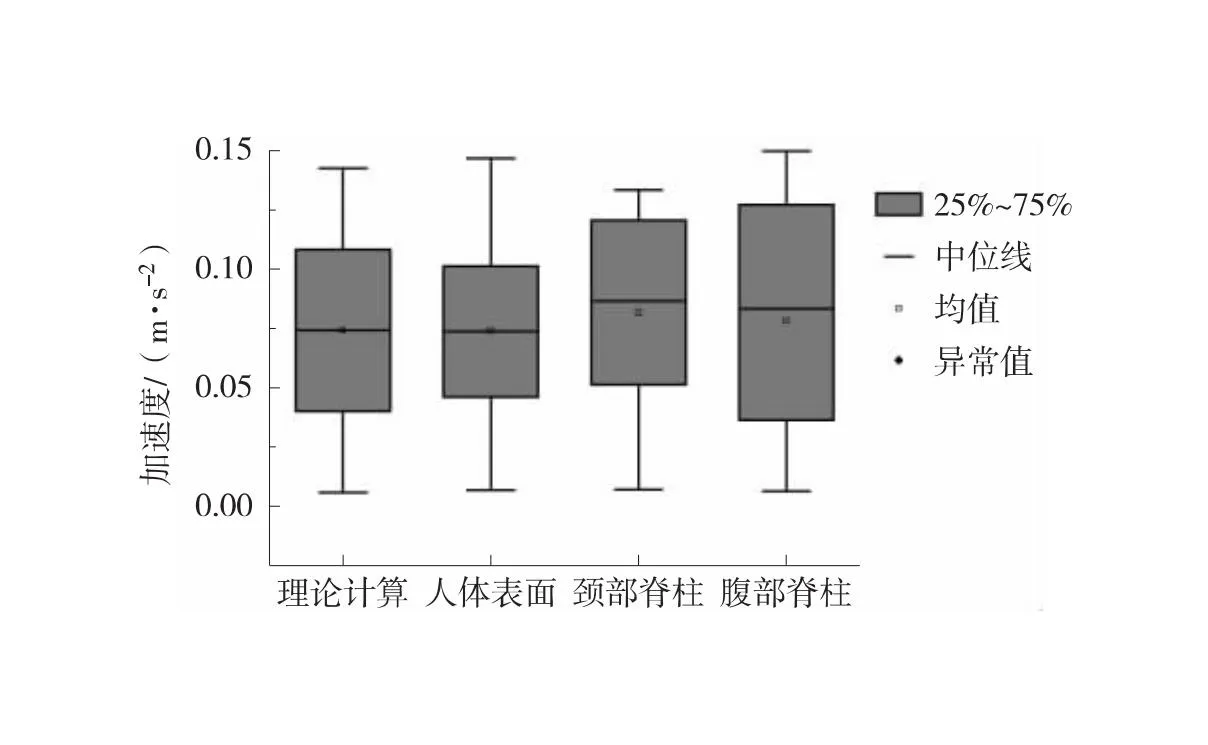
图5 不同振幅下人体模型各部位加速度统计结果

3 抑振指标限值

通过分析悬浮隧道对人体振动特性仿真结果的影响,明确影响悬浮隧道振动特性的指标为振动频率与幅值,同时分析上述仿真工况及人体各部位加速度结果,并结合振动特性人体适应性标准加速度0.2 m/s2限值,对不同振动频率与幅值产生的加速度进行限制,构建悬浮隧道跨中区域不同振动工况下人体模型腹部最大加速度结果,见表4。由表4可以看出,悬浮隧道随着振幅与频率的增加,人体模型腹部所受到的加速度值逐渐增大。

表4 不同振动工况下人体模型腹部最大加速度结果

目前悬浮隧道抑振主要通过控制振幅或频率降低隧道的振动状况,因此,在悬浮隧道设计及建设过程中,通过降低振幅或频率以控制悬浮隧道对人体产生的加速度结果。当悬浮隧道所处水域波流周期大于10 s时,即悬浮隧道频率小于0.1 Hz,在保证人体适应性的前提下,振动最大幅值不能超过0.48 m;悬浮隧道所处水域周期小于10 s时,即悬浮隧道频率大于0.1 Hz,需对振动最大幅值进行严格控制,必须将悬浮隧道最大振幅控制在0.3 m以内,才能保证人体对悬浮隧道振动没有不适感觉。

4 结论

1) 通过分析不同领域人体适应性相关研究与规范标准,结合悬浮隧道振动特性,总结提出了以0.2 m/s2为限值的悬浮隧道人体适应性标准。

2) 构建人体有限元模型,研究悬浮隧道振动条件下人体各部位动力学响应特征,并对比人体模型不同部位加速度,结果表明,人体腹部骨骼加速度明显高于人体表面与其他部位。

3) 以腹部骨骼加速度作为人体适应性的极限标准,结合悬浮隧道人体适应性标准,提出悬浮隧道不同频率下最大振幅限值,为后续悬浮隧道设计提供数据参考。