高墩多跨连续刚构桥合龙技术探讨

钟志权, 李 霖, 张赞鹏, 王国宇

(1.招商局重庆公路工程检测中心有限公司, 重庆 400067; 2.重庆市云阳县城市管理局, 重庆 400074)

连续性刚构桥属于多次超静定结构,前期施工及合龙温差导致梁体发生位移,引起主墩偏位[1];运营阶段后期由于收缩徐变也可能使得梁体发生竖向挠度和水平位移,造成主墩偏位,产生二次应力。为了消除墩顶偏位,目前通常在连续刚构桥合龙时对梁体施加顶推力,从而使墩顶发生预偏,以调节结构的内力,使其在成桥状态下更为合理[2-4]。

在顶推力的计算与优化研究方面,殷灿彬等[5]提出了消除墩顶水平位移法和消除主梁拉力法2种关于顶推力的计算方法,并通过数值分析发现,两者的计算结果基本一致,但主梁拉力法更为简捷;李胜等[6]通过有限元计算对比分析、科学测试和实桥应用等技术,提出了高墩连续刚构桥可采用不顶推合龙,并给出了判断指标;胡平等[7]分析了大吨位顶推力对铁路桥梁结构力学性能的影响,结果表明施加顶推力后主梁下挠、桥墩顺桥向水平偏位得到有效控制;梁乾敏等[8]根据工程要求确定目标函数及约束方程,建立多目标、多约束的线性规划模型,结合模糊数学法得到最优顶推力,提出一种适用于多跨连续刚构桥的合龙顶推力的求解方法;黄杜康等[9]基于敏感性分析方法构造了合龙顶推位移残差目标函数,借助Matlab优化工具对构造的约束优化问题求解得到最优修正参数,通过对模型迭代修正得到最优顶推力。

山区连续刚构桥可利用高墩的柔度来适应由预应力混凝土收缩徐变和温度效应所引起的位移,减小次内力的产生[10]。目前,针对桥梁不顶推合龙技术,既能满足受力要求,又能降低施工难度的研究较少。基于此,本文以三圣特大桥为例,建立有限元数值模型,分析推导了桥梁顶推力的计算公式,利用该计算公式进一步分析顶推力对桥梁结构不同阶段变形和受力的影响,并将有无顶推力作用下结构的位移变形和受力性能作为桥梁能否不顶推合龙的判断依据,供同类型的桥梁设计施工参考。

1 工程概况

三圣特大桥位于重庆三环高速公路合川至长寿段,其主桥为5跨预应力混凝土连续刚构桥,跨径布置为80 m+3×150 m+80 m,纵坡2%。上部结构为单箱单室变截面箱梁,箱梁根部梁高9.3 m,跨中梁高3.3 m,梁底变化曲线为1.7次抛物线;顶板与底板分别宽12 m与6.5 m,顶板悬臂长度2.75 m,全桥立面构造如图1所示。主梁采用C55高性能混凝土,纵向预应力由Φs15.2 mm的低松弛高强度钢绞线提供。

主桥桥墩采用双肢薄壁墩,双肢间距5 m,单肢截面尺寸3.5 m×8.5 m,P20、P21、P22、P23的墩高分别为84.5 m、110 m、118 m、87 m,墩身采用C40混凝土,两边跨端部采用盆式橡胶支座(GPZ(Ⅱ)7DX/SX)。桥墩采用节段浇筑施工,主梁采用悬臂浇筑施工,该桥采用挂篮合龙方式,首先完成合龙边跨,其次合龙次中跨,最后合龙中跨。

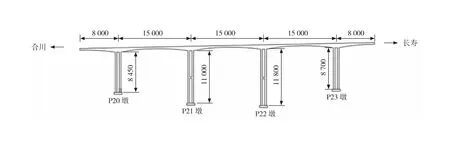
单位:cm

2 有限元建模

为分析该桥的受力和变形情况,本文采用有限元软件Midas/Civil建立全桥模型。全桥采用空间梁单元模拟,共计263个节点,248个梁单元(主梁206个,桥墩42个),有限元模型如图2所示。图2中,数字代表节点号,竖向位移以上挠为正、下挠为负,水平位移以合川至长寿方向为正。

计算荷载主要包括结构自重、二期荷载(按照50 kN/m计)、湿重、挂篮重量90 t等。主桥和桥墩的连接采用弹性连接的刚性连接模拟,确保墩梁变形同步;支座分为双向与单向支座用一般连接模拟,支座与主梁的连接采用弹性连接的刚性连接模拟,确保过渡墩支座的水平约束;墩底采用全自由度约束,模拟桥墩实际受力情况。模型按实际施工阶段划分为93个,各节段悬臂施工分为挂篮就位、混凝土湿重、混凝土浇筑和预应力张拉4个施工阶段。

3 合龙顶推力计算

本文通过理论计算得到的顶推位移量推导顶推力计算公式,再采用有限元模型确定其顶推力。

3.1 顶推位移量确定

在各合龙段对梁体施加水平顶推力,使墩顶产生与下列因素引起的水平位移值相等的反向位移。

图2 全桥有限元模型

1) 从顶推施工到成桥时间不长,顶推时考虑完全预顶抵消成桥阶段累计的墩顶位移量δ1、合龙温差引起的墩顶位移量δ2[11-12]。

2) 考虑到若预先顶推100%的30年收缩徐变后引起的墩顶位移量δ3,势必造成桥梁在成桥后长时间出现过大的反向位移,这不利于桥梁受力,故根据工程经验,一般只需顶推实际收缩徐变量的60%[13]。因此,总顶推位移量δ为:

δ=δ1+δ2+δ3×0.6

(1)

式中:δ为总顶推位移量;δ1为成桥阶段累计的墩顶位移量;δ2为合龙温差引起的墩顶位移量;δ3为30年收缩徐变后引起的墩顶位移量。

各因素作用下产生的墩顶位移量如表1所示。由表1可知,P20、P23墩的水平位移较大且较接近,P21、P22墩的水平位移较小且较接近,因此,主要以控制P20和P23墩的水平位移为主。

3.2 顶推力确定

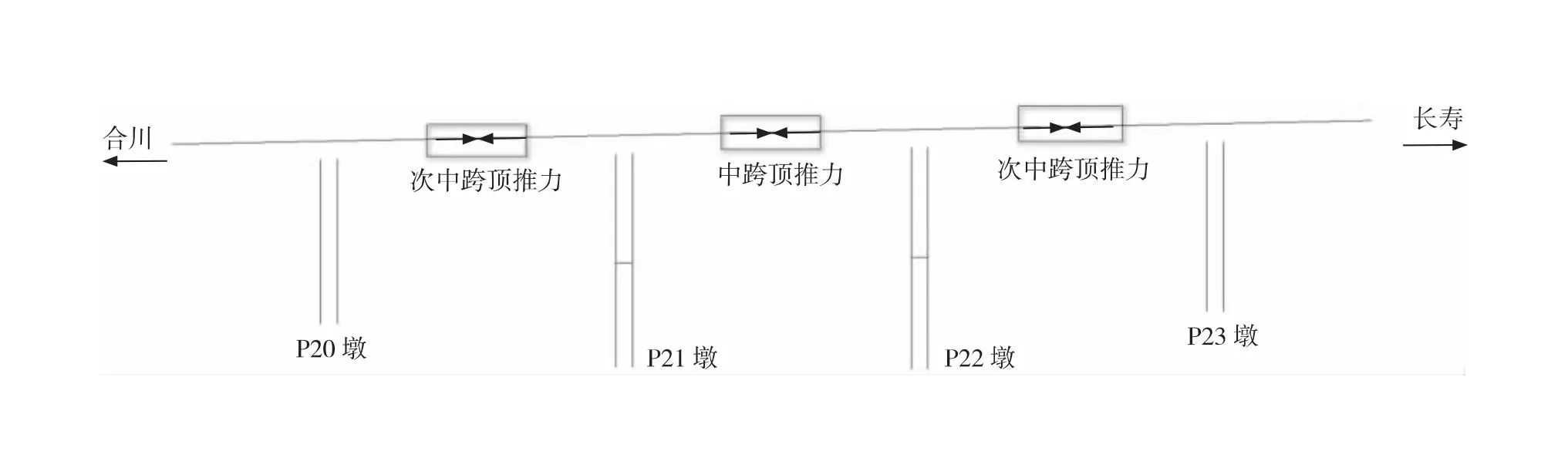
1) 顶推力施加

顶推力的施加方式如图3所示。该桥在次中跨顶推力f1、f3作用下,会产生对P20、P23墩墩顶有利的水平位移,对P21、P22墩墩顶不利的水平位移;而在中跨顶推力f2作用下,会产生对P20～P23墩墩顶有利的水平位移。

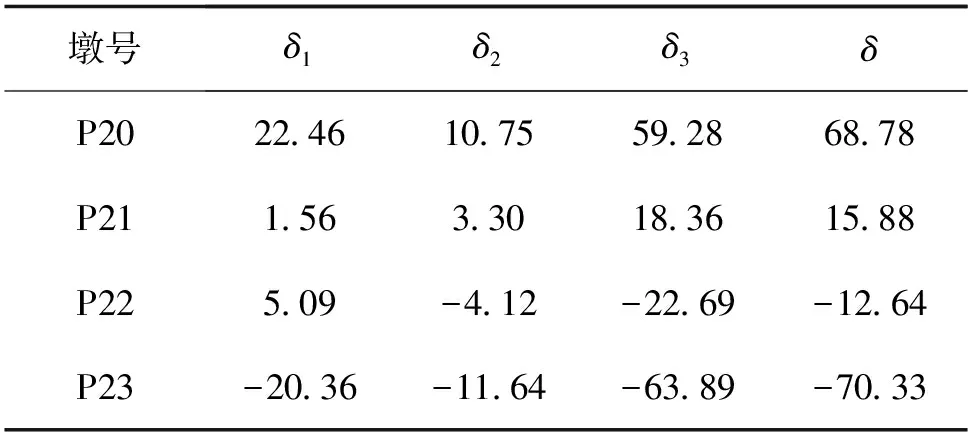
表1 各因素作用下墩顶水平位移量 mm

为得到各墩顶水平位移受次中跨顶推力和中跨顶推力的影响程度,在有限元模型中,取中跨顶推力f2=0 kN,次中跨顶推力f1、f3每级按200 kN从0 kN递增到2 200 kN;同理,假定次中跨顶推力f1、f3分别为0 kN,中跨顶推力f2每级按200 kN从0 kN递增到2 200 kN,以此得到顶推力与墩顶水平位移关系,如图4所示。由图4可知,当中跨顶推力不变时,墩顶水平位移随着次中跨顶推力的增大呈线性增大[14];同理,当次中跨顶推力不变时,墩顶水平位移随着中跨顶推力的增大亦呈线性增大,这反映了桥墩在顶推力作用下仍处于弹性阶段[15]。

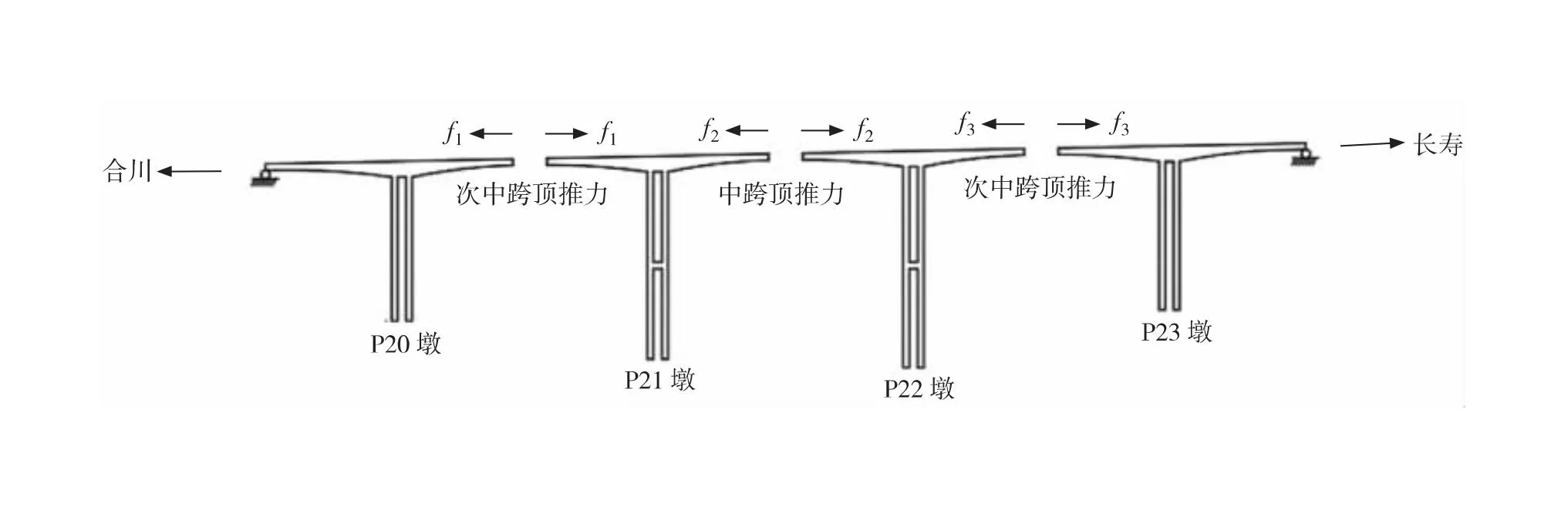
图3 顶推力施加示意

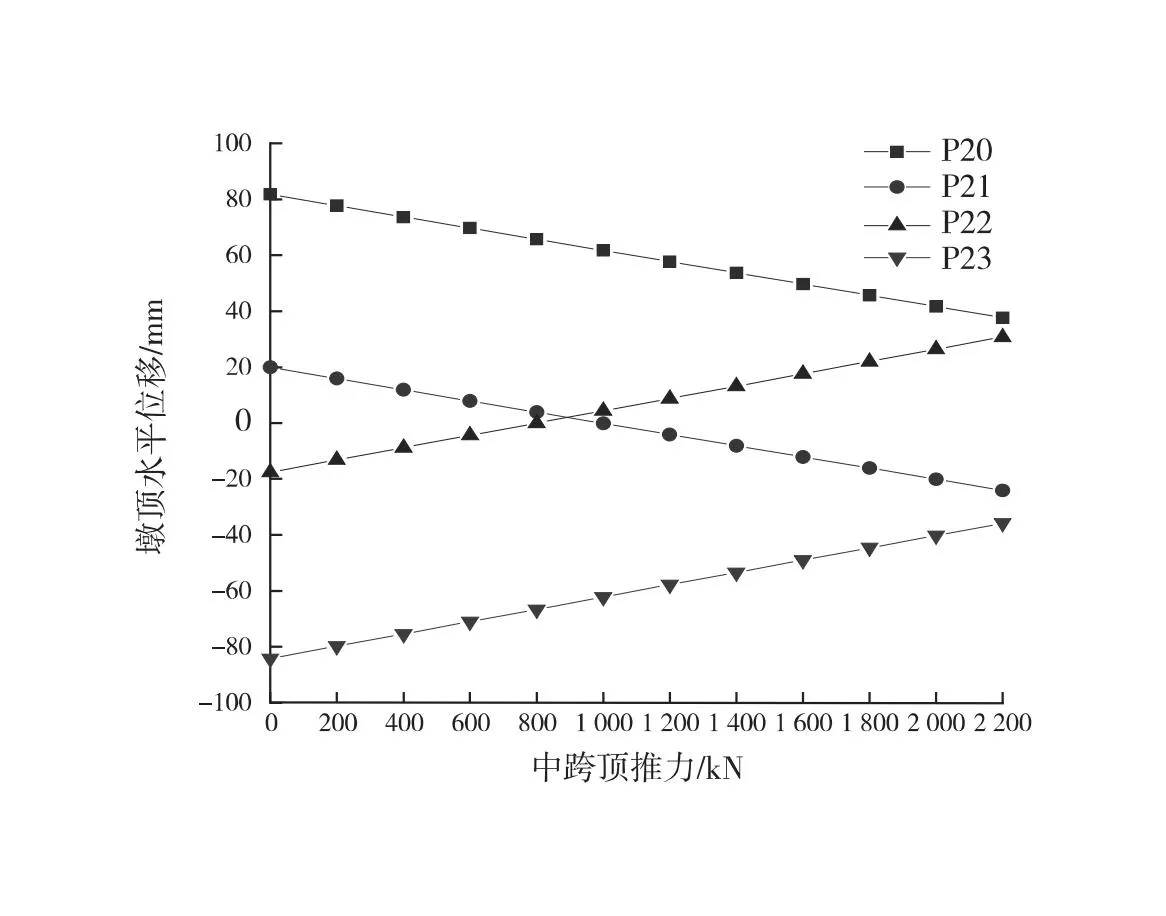
(b) 中跨

2) 顶推力与墩顶水平位移的关系

由图4可知,对P20～P23墩墩顶水平位移与顶推力进行拟合,其关系式如式(2)～式(5)所示。

P20墩:δP20=0.04f1+0.02f2

(2)

P21墩:δP21=-0.053f1+0.02f2

(3)

P22墩:δP22=-0.066f3+0.022f2

(4)

P23墩:δP23=0.043f3+0.022f2

(5)

式中:δP20、δP21、δP22、δP23分别为P20、P21、P22、P23墩墩顶总位移量绝对值,可由式(1)得到。

将表1中总顶推位移量的绝对值分别代入式(2)、式(3),得到顶推力f1=569 kN、f2=2 301 kN;同理,分别代入式(4)、式(5),得到顶推力f3=529 kN、f2=2 162 kN。

3) 顶推力确定

为保证桥梁受力平衡,需假定f1=f3,因此取两者平均值作为合龙段次中跨顶推力;同理,中跨顶推力f2也采用这2种方式计算得到顶推力的平均值。通过建立方程组求解得到f1=f3=549 kN,f2=2 231.5 kN。结合施工综合考虑,该桥次中跨顶推力为550 kN,中跨顶推力为2 200 kN。

4 不同合龙方式对桥梁受力性能和经济效益分析

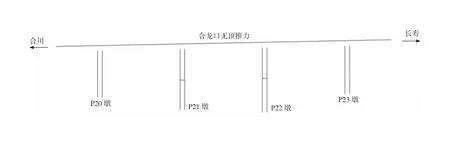
为进一步分析该桥在顶推合龙与不顶推合龙2种施工工艺下的受力性能,采用有限元软件Midas/Civil分别建立大桥顶推合龙与不顶推合龙施工成桥全过程的有限元模型,如图5所示。

4.1 桥墩墩顶水平位移量

为对比有无顶推力对墩顶位移量的影响,计算得到各桥墩墩顶水平位移量,如图6所示。不顶推合龙时,成桥阶段墩顶水平位移量较小,但30年收缩徐变后在P20、P23墩分别产生了81.74 mm、84.25 mm的较大偏位,表明若不顶推合龙,则成桥后收缩徐变将对墩顶产生较大的不利变形。顶推合龙在成桥阶段P20、P23墩分别产生了43.29 mm、52.22 mm的较大反向偏位,但30年收缩徐变后墩顶水平位移量较小,这表明通过墩顶水平位移量拟合得到的顶推力计算公式准确,理论顶推力合理,且顶推合龙产生的反向偏位将能较好地抵消未来30年收缩徐变产生的位移变形。

(a) 顶推合龙

(b) 不顶推合龙

图6 各桥墩墩顶水平位移量

4.2 桥墩受力

1) 通过数值模拟得到合龙过程中各墩墩底的最不利弯矩和应力,如图7所示。从图7可知,P20～P23墩墩底在顶推合龙与不顶推合龙2种施工工艺下均不存在拉应力,顶推合龙的各墩墩底最小压应力小于不顶推合龙的最小压应力,顶推合龙的各墩墩底最大压应力大于不顶推合龙的最大压应力。

2) 通过数值分析得到成桥及30年收缩徐变后桥墩受力变化情况,如图8所示。随使用时间的延长,顶推合龙的压应力呈减小趋势,不顶推合龙的压应力呈增加趋势,主因是收缩徐变造成桥墩向跨中偏位;在成桥阶段,顶推合龙的最大压应力较不顶推合龙的最大压应力大0.45 MPa,30年收缩徐变后,顶推合龙的最大压应力较不顶推合龙的最大压应力小1.03 MPa。P20～P23墩在顶推合龙与不顶推合龙2种施工工艺下均不存在拉应力故不会产生裂缝,且压应力小于《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[16](简称《规范》)规定的混凝土允许压应力值fcd=18.4 MPa,桥墩处于安全状态。

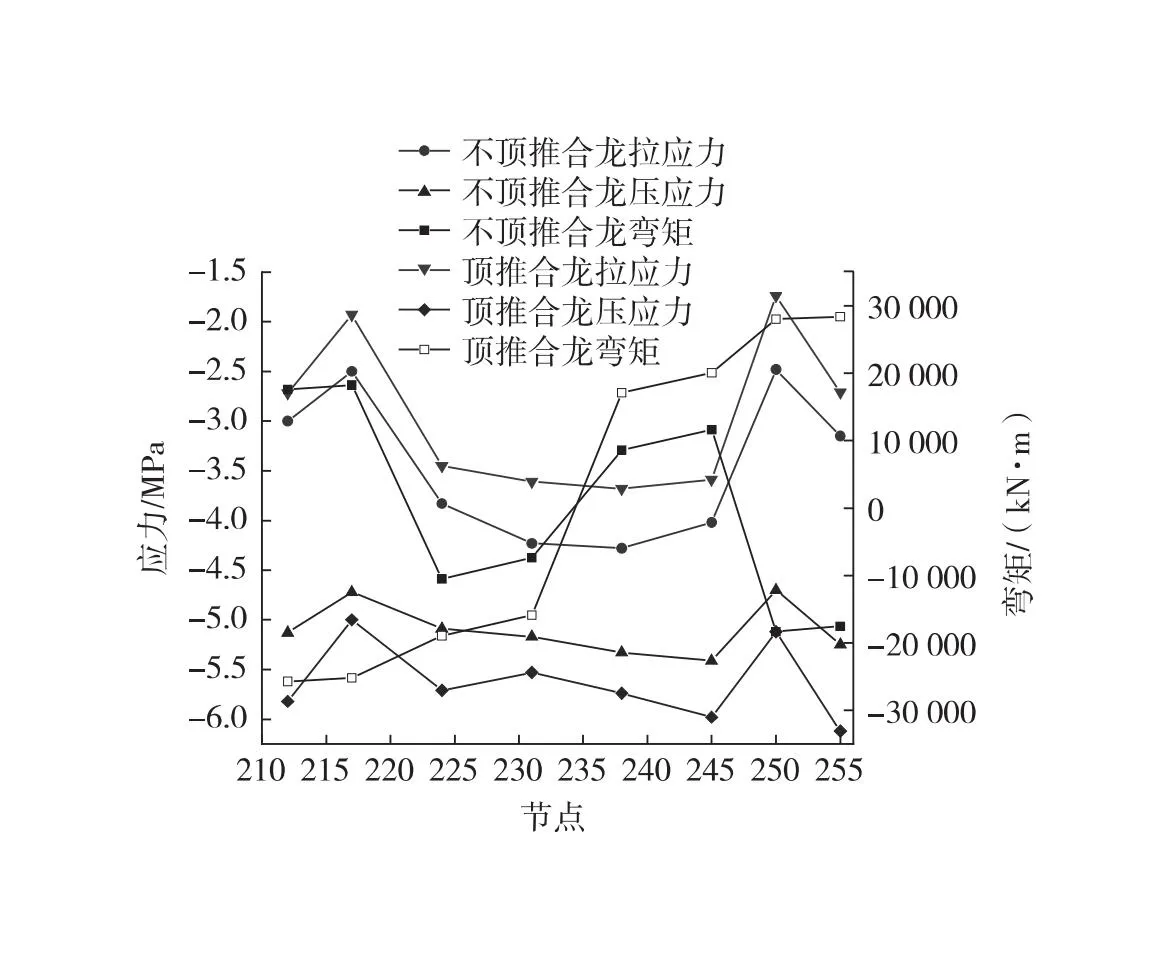
图7 合龙过程中墩底受力

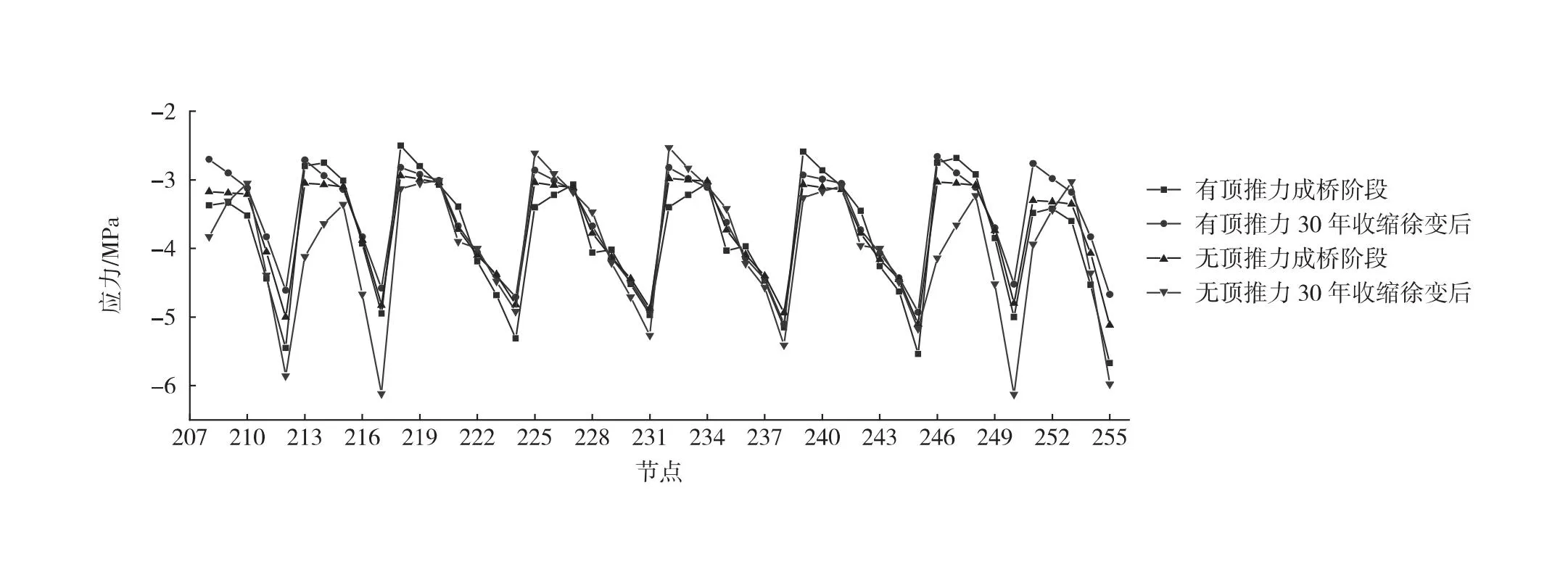
图8 墩身应力分布

4.3 主梁变形

成桥及30年收缩徐变后主梁跨中下挠值如图9所示。由图9可知,不顶推合龙的边跨挠度值较顶推合龙的边跨挠度值小,差值最大为5.07 mm;不顶推合龙的次中跨及中跨挠度值较顶推合龙的次中跨及中跨挠度值大,差值最大为17.32 mm,表明施加顶推力有利于消除后期收缩徐变等因素引起的主梁下挠,主因是在施加顶推力的过程中,导致P20与P21墩、P21与P22墩、P22与P23墩之间的主梁向上拱。在顶推合龙与不顶推合龙2种施工工艺下,30年收缩徐变对主梁变形的影响为:相较成桥,边跨产生的挠度变形与成桥方向相同,变形呈增大趋势;次中跨及中跨产生的挠度变形与成桥方向相反,呈现出与成桥相反方向的变形。

图9 主梁挠度

4.4 主梁受力

成桥及30年收缩徐变后主梁上缘和下缘应力如图10和表2所示。由图10可知,在顶推合龙与不顶推合龙2种施工工艺下,主梁上缘和下缘应力全部为压应力,且相较成桥的主梁应力,30年收缩徐变后的主梁上、下缘应力均产生显著变化,整体处于增大趋势。由表2可知,顶推合龙与不顶推合龙2种施工工艺下,主梁0号块受到的最大压应力为10.8 MPa,主梁跨中受到的最大压应力为7.88 MPa,均小于规范[16]规定的混凝土允许压应力值fcd=18.4 MPa,主梁受力满足规范要求。顶推合龙的上缘压应力与不顶推合龙的上缘压应力最大相差为0.58 MPa,顶推合龙的下缘压应力与不顶推合龙的下缘压应力最大相差为0.62 MPa。因此,顶推力的施加对主梁受力影响较小。

综上分析,不顶推合龙30年收缩徐变后墩顶将产生较大的不利变形,顶推合龙在成桥阶段墩顶产生较大的反向偏位,但能较好地抵消未来30年收缩徐变产生的位移变形。不顶推合龙的主梁挠度值较顶推合龙的主梁挠度值,边跨最大挠度差值为5.07 mm,中跨最大挠度差值为17.32 mm,表明施加顶推力有利于消除后期收缩徐变引起的墩顶变形和主梁下挠。

随使用时间的延长,30年收缩徐变后桥墩顶推合龙的最大压应力较不顶推合龙的最大压应力小1.03 MPa,桥墩在顶推合龙与不顶推合龙2种施工工艺下均不存在拉应力,且压应力小于规范[16]规定的混凝土允许压应力值fcd=18.4 MPa。在顶推合龙与不顶推合龙2种施工工艺下,主梁上缘和下缘应力全部为压应力,且主梁受到的最大压应力值为10.8 MPa,小于规范[16]规定的混凝土允许压应力值fcd=18.4 MPa;无顶推合龙的上缘压应力较顶推合龙的上缘压应力最大相差为0.58 MPa,下缘压应力较顶推合龙的下缘压应力最大相差为0.62 MPa,表明顶推力的施加对桥墩和主梁受力影响较小。

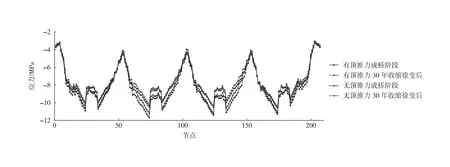
(a) 上缘应力分布

(b) 下缘应力分布

表2 控制截面位置的梁体应力

4.5 经济效益

1) 施工工艺

连续刚构桥由于独特的结构形式和受力情况,导致其合龙工序也较为复杂。合龙段的施工工期安排如表3所示。

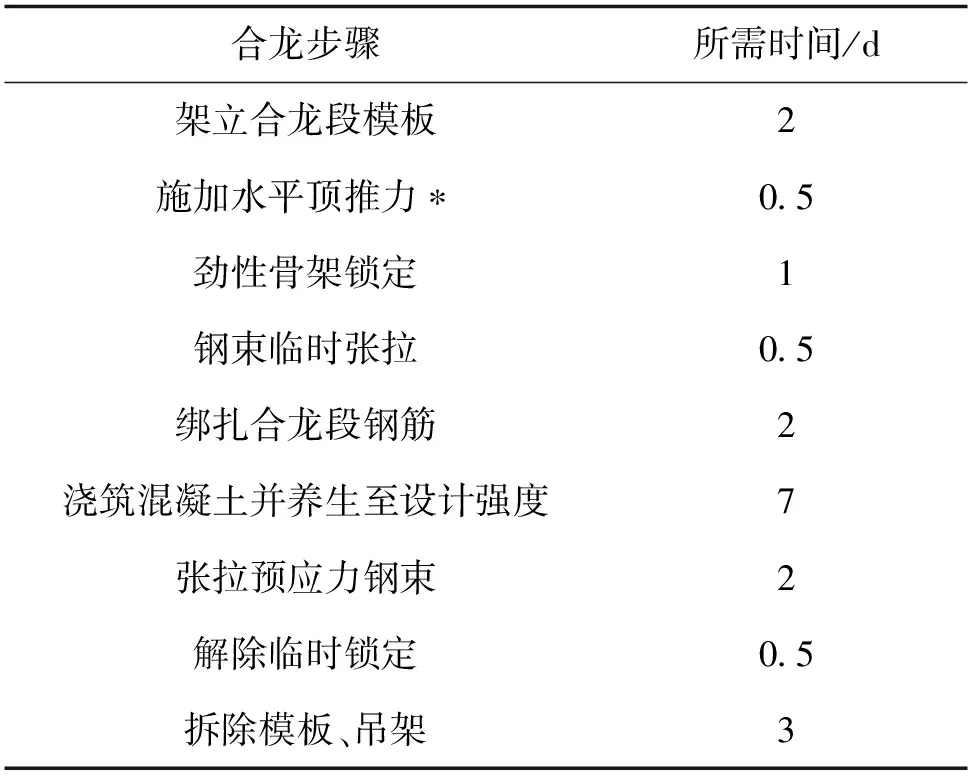
表3 合龙段施工步骤及时间安排

2) 人员配置

合龙施工拟投入的人员包括起重工、焊工、钢筋工、混凝土工、电工、机械工共计36人,另外还需专门配备指挥1人,技术员、测量、试验人员各3人。设备包括吊架3套、塔吊4台、施工升降机4台、智能张拉压浆设备3套、千斤顶、钢筋、试验仪器等。单个合龙口经济成本如表4所示。

桥梁合龙段沿边跨到中跨的合龙顺序依次合龙,2个次中跨合龙口可平行施工。若选择合龙顶推施工时,则根据表3的工期安排,顶推合龙的施工工期较不顶推合龙的施工工期多1 d;结合表4的经济成本,顶推合龙的施工成本较不顶推合龙的施工成本多2.9万元。因此,选择顶推合龙技术时将增加施工步骤,延长工期,降低工程效益,进一步增加了施工中的不稳定因素。

表4 单个合龙口经济成本

5 结论

本文依托三圣特大桥对其合龙顶推力的计算方法进行了分析,并对比分析了有无顶推力对桥梁的受力性能和经济效益的影响,得到以下结论:

1) 合龙顶推力与桥墩墩顶的水平位移量呈线性相关,桥墩墩顶的水平位移量主要由施工、合龙温差、混凝土收缩徐变等因素控制。

2) 施加顶推力虽然会导致成桥时桥墩墩顶的反向偏位过大,但也能有效改善桥梁30年收缩徐变后的墩顶变形和主梁下挠。

3) 施加顶推力能够改善桥墩的受力,当连续刚构桥桥墩较高时,墩身在顶推合龙与不顶推合龙2种施工工艺下整体均处于受压状态,不具备裂缝产生条件,且墩身的压应力未超过《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)规定的混凝土允许压应力值,桥墩处于安全状态。

4) 数值模拟结果表明,三圣特大桥梁受力均满足要求,但相较顶推合龙,不顶推合龙工艺降低了施工难度,缩短了工期,提高了工程效益,推荐采用不顶推合龙技术。