地铁站深基坑稳定性监测与数值模拟分析
刘 菁,涂 敏,张向阳,罗光财,钱 龙
(1.安徽理工大学矿业工程学院,安徽 淮南 232001;2.中国建筑第五工程局有限公司,湖南 长沙 410004)
随着国内地下轨道交通的迅速发展,大跨度深基坑地铁车站工程越来越多,工程施工对周边环境的安全性及稳定性问题亟待解决[1-3]。国内外学者采用数值分析的方法研究深基坑工程中地下连续墙的变形及土方开挖过程对周围建筑物及构筑物的影响。胡安峰等[4]基于ABAQUS模拟了某车站深基坑施工过程,证实了有限元模型能够为基坑优化设计和施工提供科学依据。周勇等[5]、李宇杰等[6]对处于红砂岩地层下深基坑的开挖支护做了详细研究,利用Midas GTS/NX有限元软件模拟出适合红砂岩地层岩性条件下深基坑支护结构形式,有效减小了基坑周边建筑物沉降。针对基坑紧邻周边建筑物工程,韩健勇等[7]利用Plaxis软件建立了二维有限元模型,并选取更适用于基坑开挖问题的硬化土模型(HS模型)作为本构方程,得出土体在开挖卸荷过程中,沉降最大值发生在距围护结构约0.6倍基坑开挖深度处。Shi等[8]采用数值模拟研究车站深基坑降水开挖变形过程及影响因素,分析不同预降水条件和不同止水帷幕深度对基坑的变形影响,指出渗流-应力在基坑降水开挖中具有明显的耦合作用,支护结构应力集中位置和最大侧向位移为0.5~0.6倍桩体开挖深度。为了快速推进工期并降低工程造价,学者们不断提出新的支护技术和方法。Yin等[9]建立数值模型,将原有的桩锚梁(PAB)支护系统改进为桩锚肋梁(PARB)支护系统,验证了数值计算模型的有效性和准确性,发现增加桩埋深对提高支护能力有较大作用,而改变腰梁尺寸对支护效果改善不明显。莫品强等[10]基于弹性抗力法提出支护桩-冠梁-支撑变形协调的计算方法。陆培毅等[11]、叶任寒等[12]分析了工程监测数据,总结出深基坑围护桩变形呈“倒三角”分布,最大位移出现在桩顶,需要对桩顶进行监测预警。周勇等[13]使用一桩两用的新型支护结构,有效缩短工期并节约成本。窦波洋等[14]通过设计常物理试验并结合数值模拟的方法发现围护桩桩顶最大水平位移约为开挖深度的0.32%。张玉成等[15]、蔡建军等[16]选用多种支护形式组合的设计方法,保证大型基坑工程建设的经济性和安全性。Peng等[17]提出的互撑+桩锚复合支护结构对相邻车站轨道变形有较好的控制作用,并证实了系统模型的可靠性。Yang等[18]设计采用1 m厚地下连续墙和850SMW 工法桩+多层内撑式组合结构,有效控制了软土层深大基坑的变形。
为进一步研究深基坑围护结构及其内支撑变形规律,本文以合肥地铁要素大市场地铁站深基坑工程为例,采用有限元软件Midas GTS/NX模拟深基坑开挖支护过程,对照现场监测数据,分析深基坑变形规律,为其他类似基坑工程问题提供一定的参考。
1 工程概况
1.1 车站概况
要素大市场车站为合肥地铁7号线一期工程第10座车站,位于徽州大道与南京路交叉口。车站外包长度为335.5 m,标准段跨度为44.7 m,覆土层厚度为2.40~4.39 m,底板埋深为16.79~19.74 m,车站主体基坑施工采用明挖顺作法。车站西南象限为绿化带及合肥要素大市场(地上7层钢混结构),车站距其地下室入口约18.7 m;其余象限建筑物离车站较远,不受基坑开挖影响。
1.2 支护结构方案
依据工程设计规范,该车站为地下二层14 m岛式站台,即是双岛五柱六跨钢筋混凝土箱型框架结构形式。采用钻孔灌注桩作为基坑的围护结构,在基坑标准段内设置两道钢筋混凝土支撑进行支护。桩墙采用φ1 000@1 300 mm的C40水下混凝土钻孔灌注桩,桩长23.6~23.8 m,相邻内支撑间隔约为9 m。
2 数值模拟有限元分析
2.1 数值模型建立及开挖工况设计
(1)数值模型几何特征及边界条件。依据土层地质条件,考虑开挖基坑相关影响因素,对土层分层进行适当简化,运用Midas GTS/NX有限元软件建立三维数值分析模型。考虑模型边界效应,数值模型尺寸取深基坑的3~5倍,具体尺寸为510 m×285 m×53 m(长×宽×高)。模型边界约束采用软件自有的固定边界程序,同时为立柱添加抗扭转约束,有效控制其在X和Y方向的位移,将要素大市场根据其整体质量等效替换为均布荷载施加在计算模型的上表面。网格划分采用混合网格生成器,对开挖区进行六面体网格加密同时兼容四面体和五面体网格过渡,模型共计网格131 438个,节点100 265个。
(2)土体本构模型选择。考虑土体的多相性、散体性和自然变异性等特点,选择Mohr-Coulomb本构模型并进行修正。修正Mohr-Coulomb本构模型可以体现不受压缩屈服影响和剪胀破坏的双硬化行为[19],有效模拟了幂函数下弹塑性和非线性弹性模型的双重组合,更适用于淤泥或砂土特性土层。依据Hooke定律,采用线弹性模型模拟基坑围护结构、内支撑、工程立柱桩等构件。修正Mohr-Coulomb模型参数见表1。
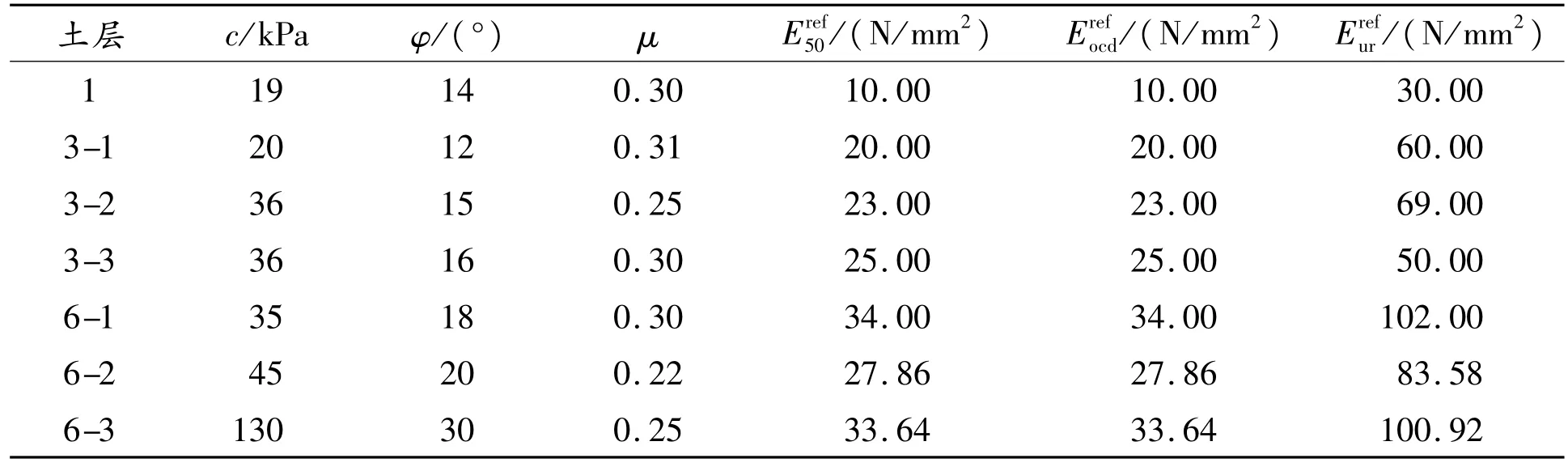
表1 土层修正Mohr-Coulomb本构模型参数
(3)围护结构模型确定。考虑到钻孔灌注桩形成的围护结构与钢筋混凝土内支撑节点的耦合作用,将钻孔灌注桩转换为受力相似的地连墙进行模拟计算[6]。根据刚度转换原理,将直径为2R、中心距为2R+t的钻孔灌注桩与长4R+t的地连墙进行转换。将最终模拟的墙厚记作H,混凝土弹性模量记作Ec,地连墙的厚度等效计算公式为
本车站基坑工程钻孔灌注桩可等效为厚度1 000 mm的地下连续墙,建模时采用板单元模拟。钢筋混凝土内支撑采用梁单元模拟。立柱桩直径为800 mm,桩长25.6 m,标准段的桩间距为9 m,桩身刚度为3×107kPa,桩的容重为25 kN/m3。图1为支护结构有限元模型。
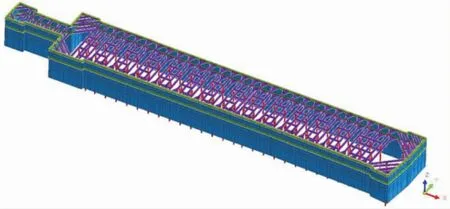
图1 支护结构有限元模型
(4)开挖工况设计。采用Midas GTS/NX特有的“施工阶段建模助手”功能设置各开挖支护施工阶段,开挖阶段各工况如表2所示。

表2 施工工况表
2.2 模拟结果分析
2.2.1 地连墙水平位移分析
地连墙水平位移值与开挖深度呈正相关,最大位移量也随着挖深逐渐下移。提取基坑的标准段所布观测点ZQT35(监测点布设如图7所示)处地连墙侧向位移模拟值,绘制位移曲线如图2。在主动土压力和钢筋混凝土内支撑的共同作用下,地下连续墙整体显现“弓形”形式的位移变化。基坑向下开挖至-1.5 m、-4.5 m、-7.0 m时,地下连墙水平位移的最大值分别为2.5 mm、7.3 mm、8.6 mm;随着基坑向下开挖至-12.35 m,地下连续墙的墙顶位移在5.1 mm上下波动,水平位移最大值发生在墙顶以下11.9 m处,为13.9 mm,曲线呈现更为饱满的“弓形”。继续向下开挖至基底17.05 m时,地下连续墙在墙顶以下15 m达到最大水平位移22.3 mm,墙底位移最终达到19.8 mm。

图2 各工况下地连墙水平位移曲线
2.2.2 基坑周边地表沉降分析
提取基坑标准段观测点DBC30处地表沉降值,绘出沉降曲线如图3所示,可以看出在不同开挖工况下,基坑周边地表沉降变化规律均大致呈现“勺形”。
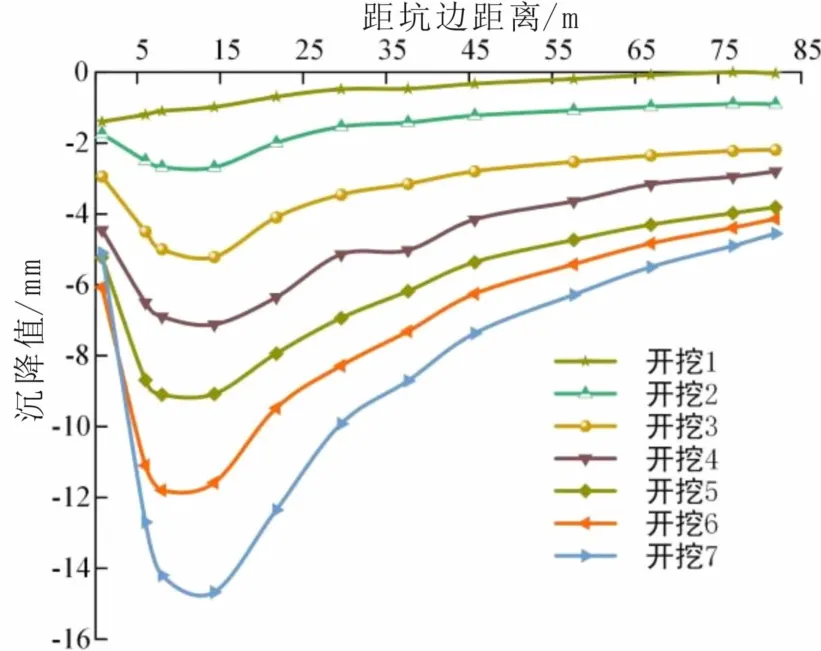
图3 DBC30断面坑外地表沉降模拟结果
当基坑开挖至地表以下7 m、12.35 m及17.05 m时,基坑周边地表最大沉降值分别发生在距离基坑边缘11.2 m、13.5 m和12.5 m处,达到5.5 mm、9.3 mm及15.4 mm。沿着基坑边缘向外,各开挖阶段地表沉降值呈现先增大后减小的变化趋势,同时发现在距离基坑约0.85倍基坑开挖深度处,地表沉降量取得最大值。开挖卸荷改变土体应力场导致土体变形,外侧土体摩擦力与大刚度地连墙共同作用遏制基坑变形,从而影响基坑周边地表沉降规律,开挖过程中围护桩后的地表沉降量小于预警值可佐证基坑始终处于稳定状态下开挖。
2.2.3 混凝土内支撑轴力分析
不同开挖阶段下各道钢筋混凝土支撑的轴力分布云图如图4所示。基坑模型中轴力最大的位置位于第二道钢筋混凝土支撑,轴力最大值达到3 510 kN,横撑的轴力相对于斜撑稍微偏大,且随着钢筋混凝土支撑的层层架设而逐渐降低。第二道支撑的及时架设使得第一道支撑轴力由峰值1 190 kN下降至985 kN,同时在同层支撑架设毗邻支撑,其轴力也明显减弱。第一道支撑的轴力最大值为1 190 kN,出现于架设始端,与监测值基本一致,第二层支撑架设后,轴力缓慢降低。统观数值模拟时各道支撑赋存的轴力值,其最大值仅占设计轴力的20%~58%,远小于预警值,基坑稳定性得到了保障。
在架设完第一道支撑继续向下开挖时(-1.5~-7.0 m),第一道支撑受到的围护墙后土压力逐步增大,轴力增大速度与其变化规律和实测数据基本吻合。在土方开挖深度增大到12.35 m时,第二道支撑效应不明显,致使第一道支撑轴力逐渐增加,但增加量只有5.05% ~6.59%,变化速率极小,最终在1 010 kN上下波动。
3 物理模型试验及分析
为分析地铁站深基坑逐步开挖过程中的基坑周边土体水平位移程度、内部应力应变特征以及基坑周围土体的沉降位移规律,利用室内物理模型试验研究不同工况下排桩支护变形规律,分析基坑开挖边缘土层内部应力应变特征。
3.1 建立相似模型
依照工程特点,为便于分析基坑开挖稳定性规律,取车站基坑标准段纵向剖面部分进行物理相似模型试验模拟,结合工程现场实际和试验平台情况,确定几何相似比为CL=CL原∶CL模=100∶1,尺寸为1.0 m×1.0 m×0.7 m(长×宽×高)。模型土参数选择要同时考虑相似判据的约束、土层的物理性质和胶结剂的性质。依据相似准则,模型土的参数选择主要考虑几何尺寸、容重和模量的相互约束关系。
以石英砂为骨料,滑石粉和酪素粉为弱胶结剂,使相似土体的密度接近真实土体[14]。采用0.7 mm粗、1.5 cm×1.5 cm网孔的热镀锌钢丝网模拟围护墙,采用孔径为7 mm的UPVC管模拟基坑内支撑。
3.2 数据采集
压力盒布设与应力监测采用振弦式土压力盒配合YJZA-32智能数字静态电阻应变仪采集开挖面两侧应力数据,并对数据进行实时采集,通过Origin数据处理软件对模型监测数据进行后处理。
在模型试验区域内,布置位移测点,采用数码相机对模型同一位置、不同时刻的像素点进行对比,以观测工作面回采过程中土体位移变化情况。在基坑研究区域加密位移测点数量,因此在模型上下部分共布置16排25列位移测点,其规格为3 cm×3 cm。
完成以上准备工作后,依次配制硬塑黏土(40 cm)、可塑黏土(5 cm)和杂填土(5 cm)。填土10 cm夯实一次,静置1 d。在填土至25 cm安置钢丝网(围护结构),用两脚图钉固定,做好标记。安放压力盒,主要沿着钢丝网边缘两侧,5 cm、10 cm、17 cm处各埋设一层。
3.3 试验结果及分析
拆模养护完成后,连通数据收集仪器线路,构成回路并进行调零,相机固定进行实时监测。按照数值模拟设置的开挖工况,每完成一次开挖,静置2 h后再进行下一步开挖;当开挖至-2 cm、-8 cm处模拟内支撑架设,每道支撑和钢丝网用热熔胶进行粘合,保证结点的耦合作用。整个过程中每隔2 s自动收集一次应变数据,应力应变位移贯穿整个试验过程。
以基坑开挖面右侧的侧壁围护结构为研究对象,围护结构水平位移随开挖过程的变化如图5所示,水平位移曲线基本呈现“弓形”。
当开挖至第一道支撑架设前(开挖1),开挖深度为2 cm,这时基坑侧壁水平位移较小,为0.2 mm;当开挖至第二道支撑架设之前(开挖3),开挖深度为8 cm,分层开挖的每个工况下基坑侧壁水平位移缓慢增大,最大水平位移发生在开挖深度5.3 cm处,为0.78 mm;架设完第二道支撑后继续向下开挖至深度为13 cm(开挖5),此时基坑侧壁水平位移最大值下移至7.5cm深度处,达到1.4 mm;当开挖深度达到17 cm至基底(开挖7),最大位移发生在开挖深度10 cm处达到了1.8 mm;待土压力释放稳定后,基底侧壁最终水平位移量保持在0.9 mm左右。
模型由开挖工况决定在基坑两侧均布设三层压力盒,每层3个,间距为25 cm,总计18个压力盒,分析基坑外侧土体因回转下沉而作用在围护结构上的侧向土压力,取每层压力盒变化值加权平均,其变化规律如图6所示。随着支撑的架设,边缘土体的下沉得以控制,下沉量减小,压力盒压力值增量减小。

图6 基坑侧壁土压力变化规律
4 现场监测方案及结果分析
4.1 监测方案
对地连墙、基坑周边地表、建筑物和内支撑轴力等指标进行全过程监测量控,围护墙侧向位移和周边地表沉降的累计绝对值均不超过30 mm,累计开挖深度不超过0.20%,变形速率不大于3 mm/d,支撑轴力不大于6 000 kN。监测点的布设见图7。

图7 基坑监测点平面布置
4.2 监测结果分析
(1)围护墙顶水平位移。
深基坑中土体卸荷产生侧向土压力,导致土体产生水平位移。相较于其他监测指标,支护结构各部分与土体及外界因素的耦合作用造成了支护结构的变形,产生这种变形的本质是结构内力的变化与调整。围护结构墙顶水平位移是基坑变形监测的重要内容之一。本文选择了基坑周围的4个监测点ZQT35、ZQT39、ZQT41和ZQT17的实测值进行研究,分析支护墙墙顶的水平位移值随时间的变化(见图8)。
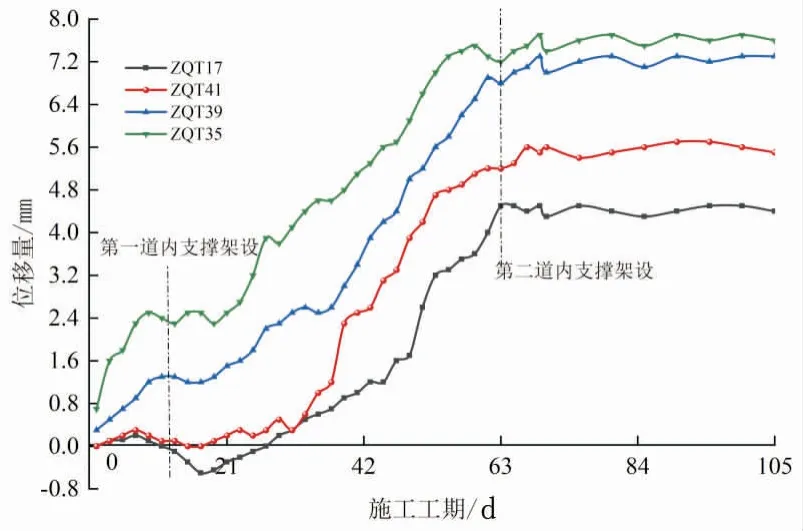
图8 墙顶水平位移随时间的变化关系
由图8可知,基坑内围护墙顶的水平变形在不同的施工阶段明显不同。监测点ZQT35、ZQT39、ZQT41及ZQT17从近到远布置在基坑标准段的中间位置,各监测点的最大水平位移值分别为7.4 mm、6.7 mm、5.2 mm、4.5 mm,说明基坑周围土体水平位移分布不均衡,围护墙顶位移最大值出现在基坑中部。各个监测点的位移量均远小于控制值30 mm,表明施作冠梁和钢筋混凝土内支撑对地下连续墙墙顶的水平移动起明显约束作用,在开挖过程中基坑安全可控。
(2)基坑周边地表沉降分析。
监测点DBC09-1、DBC12-2、DBC27-2、DBC30-3、DBC32-3及DBC35-3的地表沉降监测数据整理分析如图9所示。随着基坑不断向下开挖,土体卸载量增大,地表沉降较快,监测点DBC35-3最大沉降量在14.3 mm上下波动,直至开挖至基底施作结构层时,基坑附近的地表沉降趋于稳定。
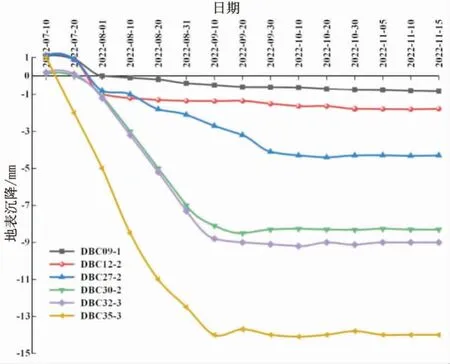
图9 基坑周边地表沉降监测数据
(3)轴力分析。
基坑架设两道钢筋混凝土支撑,轴力设计值均为6 000 kN。监测点ZCL10的两道内支撑轴力随时间的变化曲线如图10所示。架设第一道钢筋混凝土支撑后,由于混凝土硬化后收缩,初始压应力为1 350 kN。第二道支撑架设完成后,很大程度上分担了基坑土层卸载产生的压力,第一支撑的轴力显著下降。当基坑继续开挖至地下12.35 m时,第二道支撑轴力达到了峰值3 680 kN,说明受力主要下移到基坑中下部,在开挖接近完成时支撑轴力变化缓慢且逐渐趋于稳定。
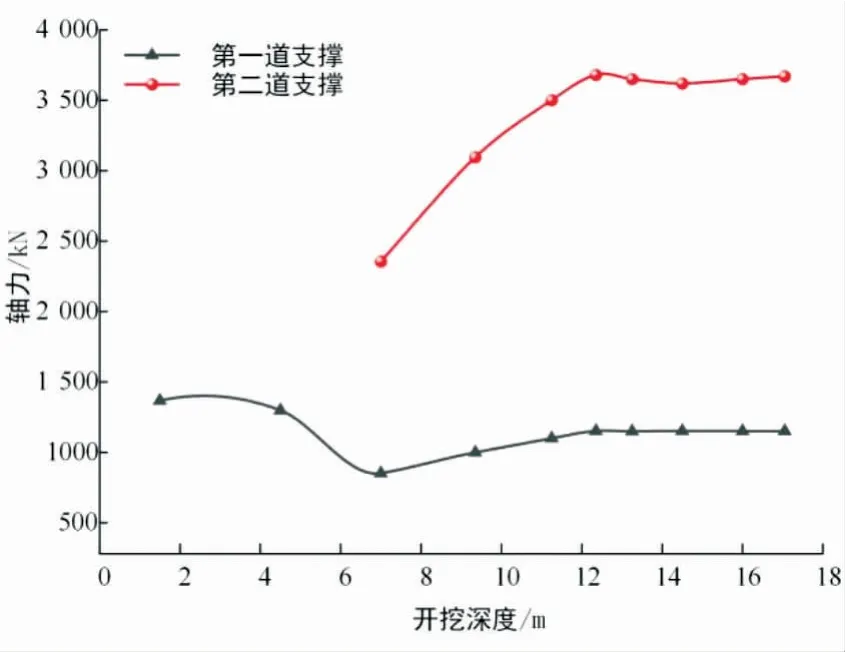
图10 ZCL10处内支撑轴力曲线
5 结论
本文基于Midas GTSNX有限元软件建立三维数值模型,借鉴相似模型试验,结合现场实测,深入分析了排桩支护的水平位移、内支撑轴力以及基坑周围地表沉降等指标的相关变化规律。结论如下:
(1)深基坑围护结构的水平位移量与其开挖深度呈正相关,开挖中随着内支撑的逐步架设,地下连续墙的水平位移曲线逐渐呈现出“弓形”的变化规律,最大位移的部位逐渐下移,在地表以下15 m处达到峰值22.3 mm。随着基坑开挖深度加大,基坑周围地表沉降累计值增加,逐渐呈现“勺形”的变化规律,在距基坑边缘12.5 m处达到最大沉降值15.4 mm。
(2)第二道支撑的及时架设会使第一道支撑轴力由峰值1 190 kN下降至985 kN,土体开挖卸荷产生的土压力重分配,由两道支撑共同承担。当开挖深度达到12.35 m时,第二层支撑承担的轴力作用将不再明显,而第一道支撑轴力增加,但轴力的增加速度下降,为5.05%~6.59%。
(3)采用物理相似试验从宏观上揭示了开挖深度与侧向坑壁变形和压力呈正相关变化,随深度的增加,围护墙最大水平位移量出现在模型开挖至10 cm处,达到1.8 mm,约为开挖深度的0.18%,基坑开挖时其侧向土压力变化趋势与实际工况基本吻合。

