JH区块沙溪庙组致密砂岩气藏压裂缝高影响规律研究

肖红林, 黎 凯, 侯 甫, 罗 皓, 唐慧莹

(1.中国石油西南油气田分公司, 成都 610051; 2.川庆钻探井下作业公司, 成都 610051; 3.西南石油大学 油气藏地质及开发工程国家重点实验室, 成都 610051)

致密砂岩气藏是指在覆压条件下储集层的孔隙度低于10%、基质的有效渗透率低于0.1 mD的砂岩气藏,是非常规天然气勘探开发的重要领域之一[1-4]。致密砂岩气藏作为一种非常规油气藏,在我国分布广泛,主要集中在鄂尔多斯、四川、松辽、塔里木等盆地。其中“以气为主”的四川盆地是目前已发现的国内八大致密油气重点探区之一,具有十分重要的典型性和代表性。侏罗系沙溪庙组和上三叠统须家河组是主要的致密砂岩气储层,其具有埋藏浅、气质高、开发快等优势,因此已成为当前勘探开发的重要焦点之一。四川盆地JH区块沙溪庙组致密砂岩气资源丰富,勘探开发潜力大,是西南油气田分公司“十四五”致密气核心建产区块[5-6]。JH区块沙溪庙组为一套陆相砂泥页岩地层,河道砂体广泛发育,砂体厚度多为20～25 m,储层岩石主要为长石岩屑砂岩,孔喉半径为0.01～1.54 μm,孔隙度介于10%～15%,渗透率介于0.1～1 mD,为低孔、低渗孔隙型致密储层,大规模水力压裂是实现致密砂岩气藏规模效益开发的关键技术[7-10]。然而在水力压裂过程当中,裂缝高度控制是一件很棘手的问题:储层不存在隔层或隔层应力较弱时,裂缝可能会在垂直方向上过度延伸,穿透产层与非储层、含水层发生沟通,造成产层含水暴增,导致压裂效果很差,影响油气采收率,同时缝高过大会浪费过多的压裂材料,影响经济效益[11-12]。因此,在进行压裂施工之前有必要对裂缝纵向延伸范围进行预测,以便合理设计施工层位和压裂施工参数。针对此问题,目前国内外学者针对压裂过程中裂缝高度控制因素进行了分析研究,对缝高影响因素形成了一定认识。

贺甲元等[1]通过建立裸眼水平井缝高模型,建立区块A内裸眼水平井压裂裂缝高度与施工排量的计算模型;王明星等[2]通过压裂物理模拟实验发现高层间模量差对缝高扩展不会起到明显的抑制作用;但张矿生等[3]却提出了相反的结论,认为高模量地层对缝高的扩展有一定的限制作用;Simonson等[13]、张庆辉等[14]基于线弹性断裂力学理论研究表明,储隔层应力差、压力梯度效应是影响缝高的主要因素;Teufel和James[15]、Warpinski和Teufel[16]通过室内试验研究表明,储隔层最小水平主应力差是防止裂缝进入隔层的最重要因素,并通过弹性有限元计算得出了在不同岩性组合下,控制压裂裂缝高度所需的最小地应力差值;Daneshy[17]研究发现,压裂过程中储隔层界面在发生剪切破坏时会导致裂缝尖端发生钝化从而阻止裂缝的局部生长;Yue等[18]、Huang等[19]、Gao和Ghassemi[20]基于有限元方法、室内试验和离散元等方法研究发现,裂缝从刚性地层向软地层扩展时会受到明显的抑制作用;景东阳等[21]、吴锐等[22]、王瀚[23]基于ABAQUS有限元计算平台建立了三维层状介质压裂缝高模型,研究发现影响裂缝高度扩展的最重要因素是储层应力差,其次是杨氏模量和泊松比;胡阳明等[24]、李勇明等[25]、罗志锋等[26]通过有限元方法、数值模拟等技术对影响缝高的地质工程因素进行研究表明,控制缝高可以通过增大储隔层应力差、减小压裂液规模和压裂液黏度等方法;Cong等[27]建立了基于三维离散格子法的裂缝高度传播模型研究发现高杨氏模量、低排量、低黏度可以有限地控制裂缝高度生长;Morales等[28]、Garcia等[29]研究发现通过添加人工隔层的方法可以有效的限制裂缝的高度。

综上所述,大量学者通过室内试验、有限元方法、数值模拟等方法研究了应力差、杨氏模量差、储隔层界面性质等地质因素和施工排量、压裂液黏度等工程因素对水力压裂过程中裂缝垂向扩展的影响规律,取得了相应的研究成果。但由于不同地区储层间性质差异较大,各参数对缝高的影响规律并不完全一致,同时模拟实验参考现场资料较少,因此不能简单地套用已有的研究成果。

JH区块尚处于勘探开发初期,压裂施工设计经验不足,缺乏裂缝高度方向延伸规律和认识。因此,基于JH区块储层特征参数,建立等效层状地质模型,基于多种裂缝扩展模型,利用现场压裂施工数据和井温测井缝高数据,现场与模拟相结合优选裂缝模型。基于优选的模型,研究地应力、杨氏模量、泊松比、施工排量、压裂液性能等对裂缝垂向扩展行为的影响和控制作用。研究结果可为JH区块现场水力压裂预测缝高、优化压裂施工参数及规模开发提供参考。

1 水力裂缝缝高扩展数学模型

在早期的水力压裂模拟过程中,由于储层复杂性较低,施工规模较小,一般采取二维裂缝模型PKN(Perkins-Kern-Nordgren)和KGD(Khristianovic-Geertsma-de Klerk)来模拟裂缝的扩展[30-31]。随着非常规油气资源的勘探开发,常规水力压裂模型已经无法满足水力压裂模拟需求,为此学者们提出了拟三维模型、平面三维模型、全三维模型以及考虑复杂层理结构、断层、天然裂缝等复杂储层结构的复杂裂缝模型[32-34]。水力压裂裂缝模拟的最终目标是用于压裂设计和分析,本文中以常用的拟三维、平面三维和非常规裂缝模型开展裂缝扩展模拟。

1.1 拟三维裂缝模型(Pseudo 3D,P3D)

P3D模型在垂直方向用二维裂缝模型的解释方法描述裂缝的延伸,运用断裂力学中的裂缝扩展准则处理裂缝高度变化的影响,并假定裂缝是一个垂直面,对每个垂直截面作二维平面应变假设,沿着裂缝的长度分成许多单元,每个单元可以有不同的高度。然而,其中重要的一个假设是裂缝是在比相邻层应力更低的层中开始和扩展的,对于没有应力阻挡层的地层,特别是裂缝高度增长到应力低于射孔层的地层时,P3D模型可能导致预测裂缝高度的显著误差[35-36]。

裂缝高度方程:

(1)

式中:KI2、KI3分别为缝高上尖端、下尖端的应力强度因子,Pa·m0.5;l为半缝高;p为储层压力;p(z)为缝内流压;z为裂缝纵向延伸坐标。

令KI2=KIC2,KI3=KIC3,可得裂缝高度控制方程:

(2)

式中:半缝高l=h(x,t)/2,h(x,t)为t时刻x处的缝高,m;KIC2、KIC3分别为盖层和底层断裂韧性,Pa·m0.5;S1、S2、S3分别为产层、盖层、底层的最小水平主应力,Pa;Hp为产层有效厚度,m;hu、hl分别为缝内x处从产层中点算起的裂缝上扩缝高、下延缝高,m。

1.2 平面三维裂缝模型(Planar 3D,PL3D)

平面三维(PL3D)采用三维固体方程计算岩石变形,假定裂缝在一个平面内传播,并且平面方向和最小水平主应力垂直,通过裂缝边界确定裂缝长度和高度,计算量较大。裂缝上、下高度控制方程[37-38]为

(3)

式中:Kuc为盖层与顶层岩石的断裂韧性,Pa·m0.5;Klc为盖层与底层岩石的断裂韧性,Pa·m0.5;gv为缝高摩阻压降梯度引起的压力梯度,Pa/m;gs为缝高摩阻地应力梯度引起的压力梯度,Pa/m;gρ为流体重力引起的压力梯度,Pa/m;h为产层半高,m;Su为盖层与产层的最小水平主应力差,Pa;Sl为底层与产层的最小水平主应力差,Pa。

1.3 非常规裂缝模型(unconventional fracture model,UFM)

非常规裂缝模型由Kresse等[40]提出,可以很好地处理裂缝网络中流体流动与裂缝弹性变形的全耦合问题,与常规拟三维裂缝模型拥有相似的假设条件和控制方程。裂缝顶部和底部尖端的应力强度因子是根据裂缝内部的压力、裂缝几何形状和层应力计算得出的,通过将尖端处的应力强度因子与包含裂缝尖端的层中的断裂韧性相匹配来确定稳定的裂缝高度[39-40],其裂缝高度方程为

(4)

(5)

式中:pcp为在参考深度hcp底端测量的裂缝压力,Pa;z为裂缝所在位置,m;ρf为流体密度,kg/m3;KIu、KIl分别为裂缝上下尖端应力强度因子,Pa·m0.5;w(z)为深度z处裂缝宽度,m;σn、σi分别为顶端和第i层的地应力,Pa;h为裂缝高度,m;hi为从底层到第i层顶部的高度,m;E为杨氏模量。

2 裂缝扩展模型优选

2.1 压裂模型建立

结合JH区块沙溪庙组二段储层物性、岩石力学参数和施工数据(表1),使用斯伦贝谢一体化软件Petrel建立泥页岩-砂岩-泥页岩三层储盖层等效模型(图1),上下隔层、中间储层厚度均为20 m,模型大小为300 m×50 m×60 m,平面网格步长10 m×10 m,纵向网格2 m,水平井及射孔均位于模型中心。

图1 压裂模拟模型

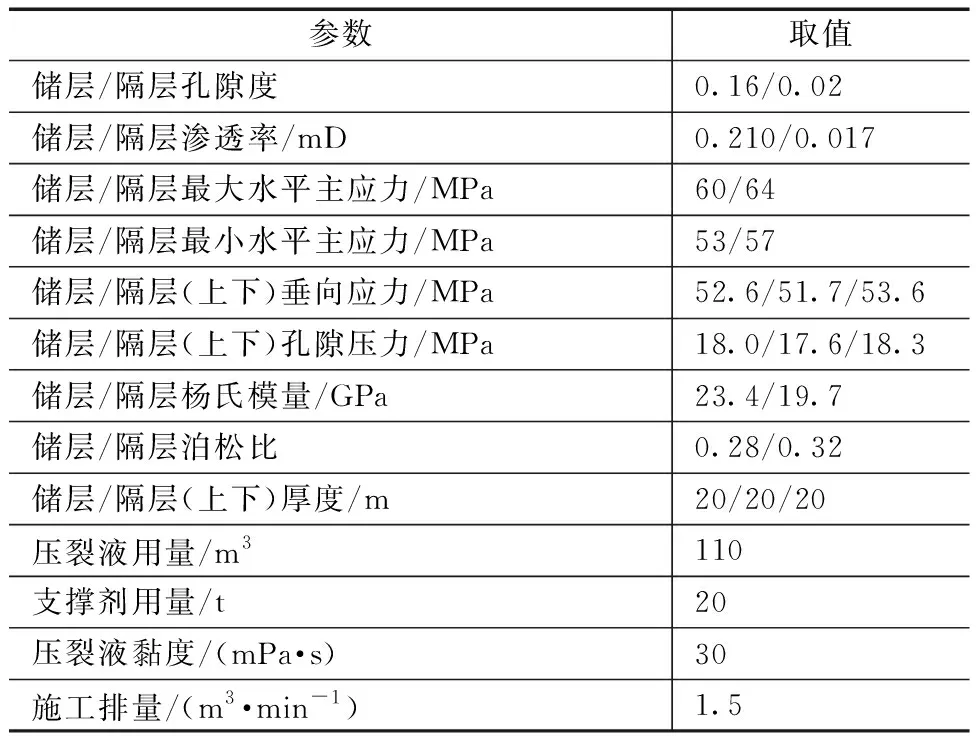
表1 压裂数值模型输入基本参数

2.2 裂缝扩展模型优选

选取3口具有代表性的井,从井温测试曲线(图2)分析:XQ1井裂缝上界面在2 422.0 m,裂缝下界面在2 435.0 m,裂缝高度为19.0 m;YQ8井压裂缝高裂缝上界面在1 728.5 m,裂缝下界面为1 746.0 m,缝高为17.5 m;YQ10井靠上压裂段裂缝上界面在1 788.0 m,裂缝下界面在1 807.0 m,裂缝高度为19.0 m,靠下压裂段裂缝上界面在1 826.0 m,裂缝下界面在1 848.0 m,裂缝高度为22.0 m。由上述井温测井曲线分析可知,各井压裂后裂缝高度主要分布在17.5～22.0 m。

分别利用P3D、PL3D和UFM模拟实际施工条件下的裂缝高度,模拟结果如图3所示。模拟结果显示P3D模拟缝高为22.17 m,UFM和PL3D模拟缝高分别为32.17 m和40.32 m,P3D裂缝扩展模型模拟缝高更接近井温测井缝高值。拟三维模型(P3D)在缝高模拟准确度方面更具优势,因此选择P3D裂缝扩展模型来进行缝高控制机理的研究。

3 地质因素对裂缝高度的影响

3.1 储隔层应力差

目前研究表明当油气层和上下遮挡层之间的最小水平主应力差(以下简称应力差)达到2 MPa以上,隔层将对裂缝的垂向延伸起较强的抑制作用,但隔层过薄也会发生穿层现象;应力差值达到6 MPa,隔层缝高控制能力很强,基本能够将裂缝完全控制在产层内[41]。而对于不同地层,阻止裂缝高度延伸的隔产层应力差不尽相同。

为了进一步明确河道砂致密砂岩气藏压裂过程中砂岩和泥页岩层应力差对缝高的控制作用和影响规律,利用表1数据,通过设定其他因素不变,逐渐改变隔层的水平最小主应力。在一般情况下,砂岩储层上下遮挡层为泥页岩,其应力大于砂岩储层,保持其他参数不变,设置储隔层间地应力差(隔层与储层的差)分别取为0、1、2、3、4、6、8、10 MPa,研究其对压裂缝高的影响。模拟结果显示裂缝呈上下对称分布,因此以最大缝高处半缝高值和裂缝宽度值绘制裂缝等效示意图,结果如图4所示,当应力差较小时,裂缝呈现“细长”型形态,随着应力差的增大,裂缝形态变为“短粗”型,最小水平主应力差值越大,缝高越小,缝宽越大,裂缝纵向延伸受到的限制越强。这是因为地应力差值越大,抑制裂缝延伸的闭合压力增大,减小了作用于裂缝壁面的净张开压力,裂缝高度减小。

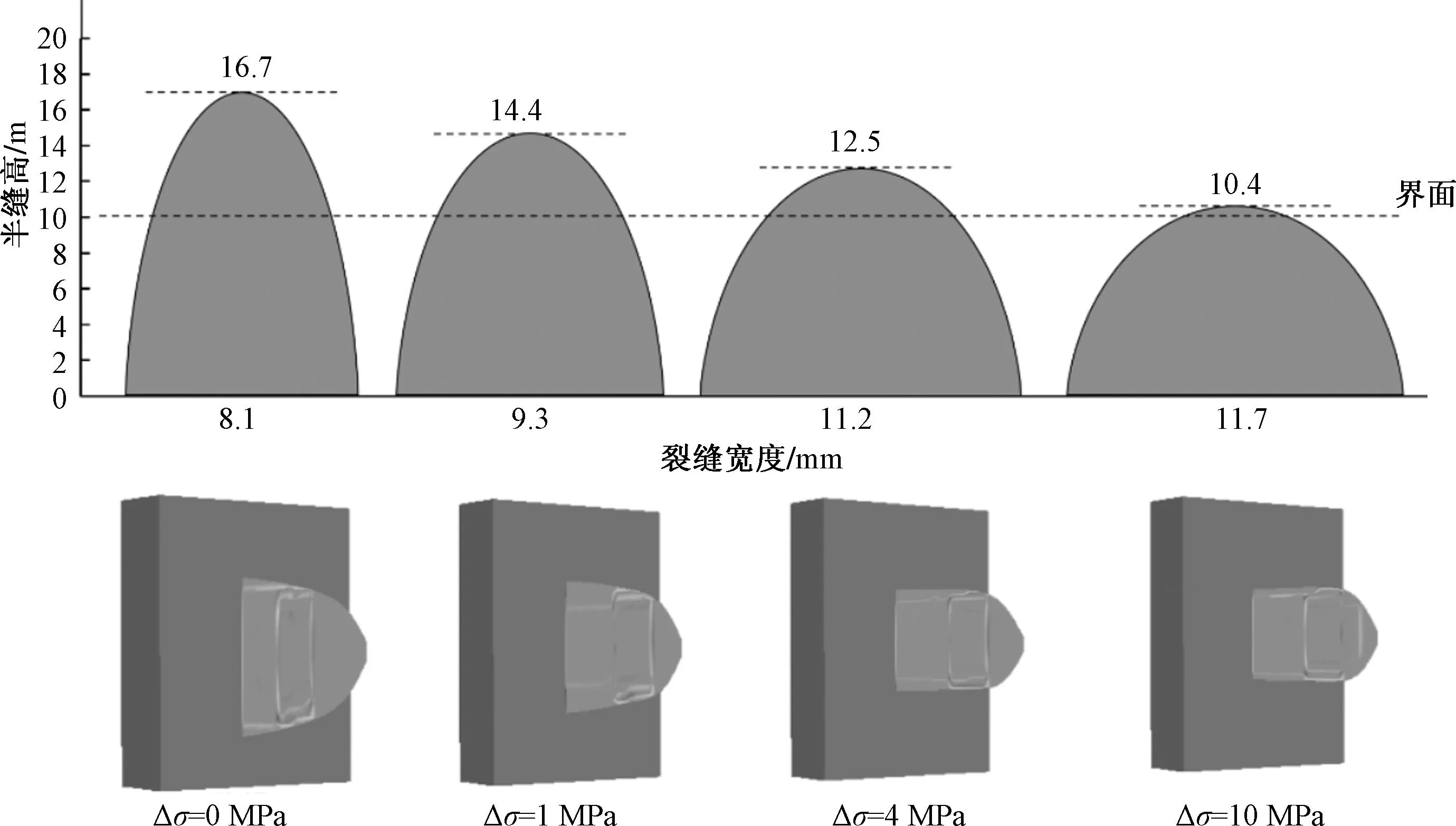
图4 应力差对裂缝高度的影响

绘制不同应力差下缝高缝宽变化曲线和裂缝穿深(裂缝穿层深度,简称穿深)变化幅度曲线,如图5和图6所示,随着应力差的增大,裂缝穿层现象逐渐减弱:当应力差为0 MPa时,裂缝高度达33.35 m,裂缝穿深约13.35 m,存在严重的穿层现象;当应力差为2 MPa时,裂缝向隔层延伸深度迅速减小至5.09 m,裂缝穿深减小幅度61.87%;当应力差为4 MPa时,缝高受到明显的抑制,穿层深度仅2.35 m,穿深减小幅度达82.4%;在应力差达到6 MPa及以上,裂缝高度基本限制在储层内部不再发生变化。因此在针对实际压裂施工过程中不存在隔层或储隔层应力差较小的情况下,可以使用人工隔层的方法进行缝高控制。

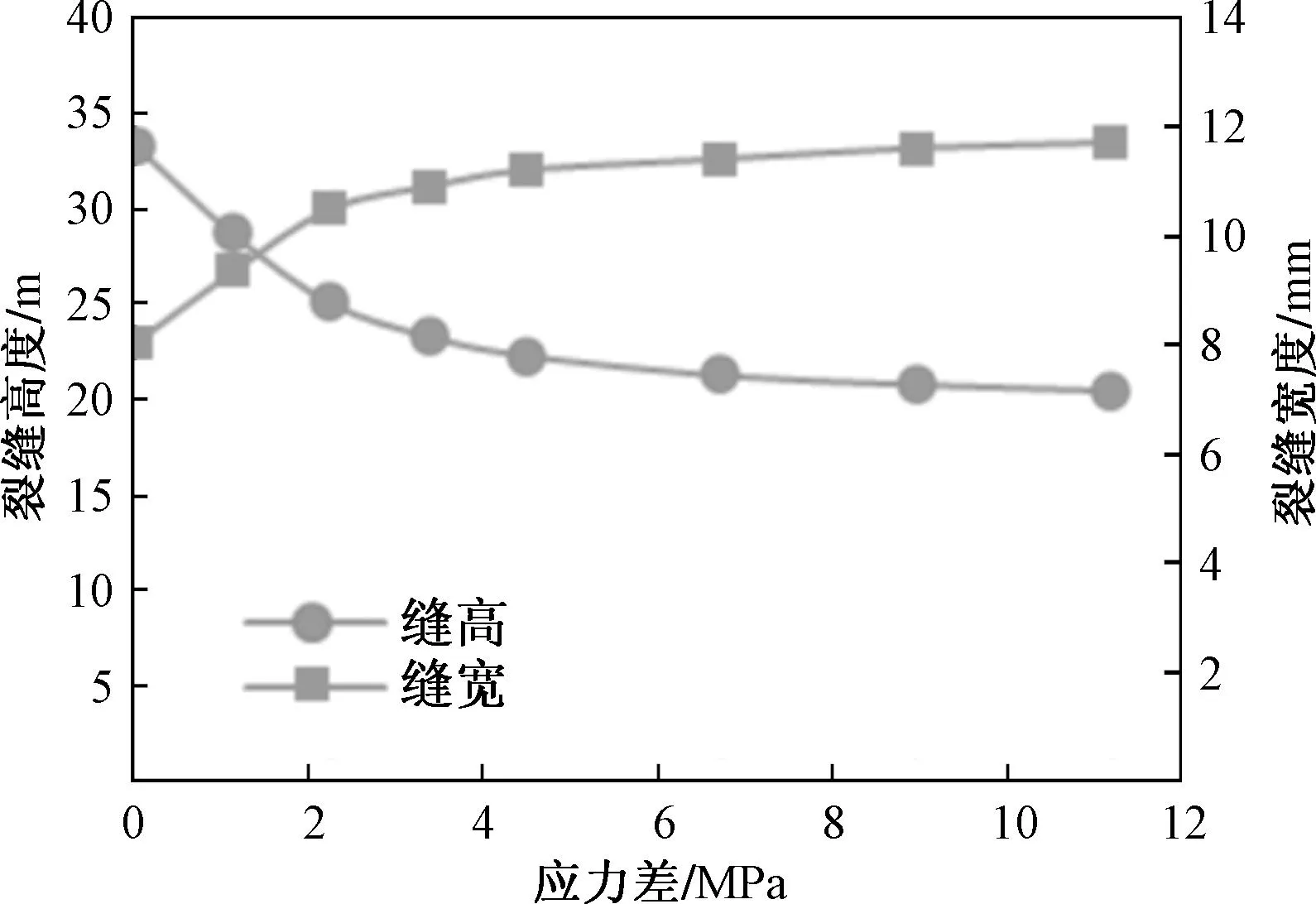
图5 不同应力差下缝高、缝宽变化曲线

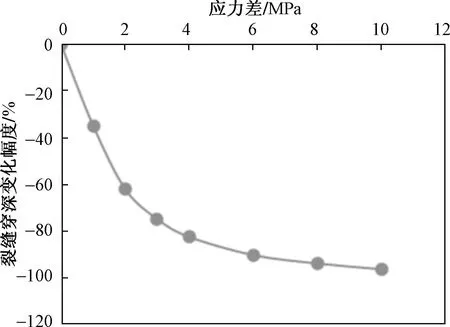
图6 不同应力差下裂缝穿深变化幅度曲线

3.2 杨氏模量

为了探究不同储隔层模量差异对缝高扩展的影响规律,在储隔层应力差分别为0 MPa和4 MPa的前提下,保持其他参数不变,设置储层杨氏模量为23 GPa,同时考虑储层为低模量和高模量两种情况下缝高的扩展情况:当储层为高模量时,设置隔层杨氏模量为1.15、2.3、4.6、11.5、23 GPa,对应储隔层杨氏模量倍比(储层杨氏模量与隔层杨氏模量比值)为20、10、5、2、1;当储层为低模量时,设置隔层杨氏模量为23、46、115、230、460 GPa,对应储隔层杨氏模量倍比为1、0.5、0.2、0.1、0.05,其模拟等效示意图如图7所示。在不同应力差下,随着杨氏模量倍比增大,缝高减小,缝宽增大,裂缝形态由“细长”型变为“短粗”型。

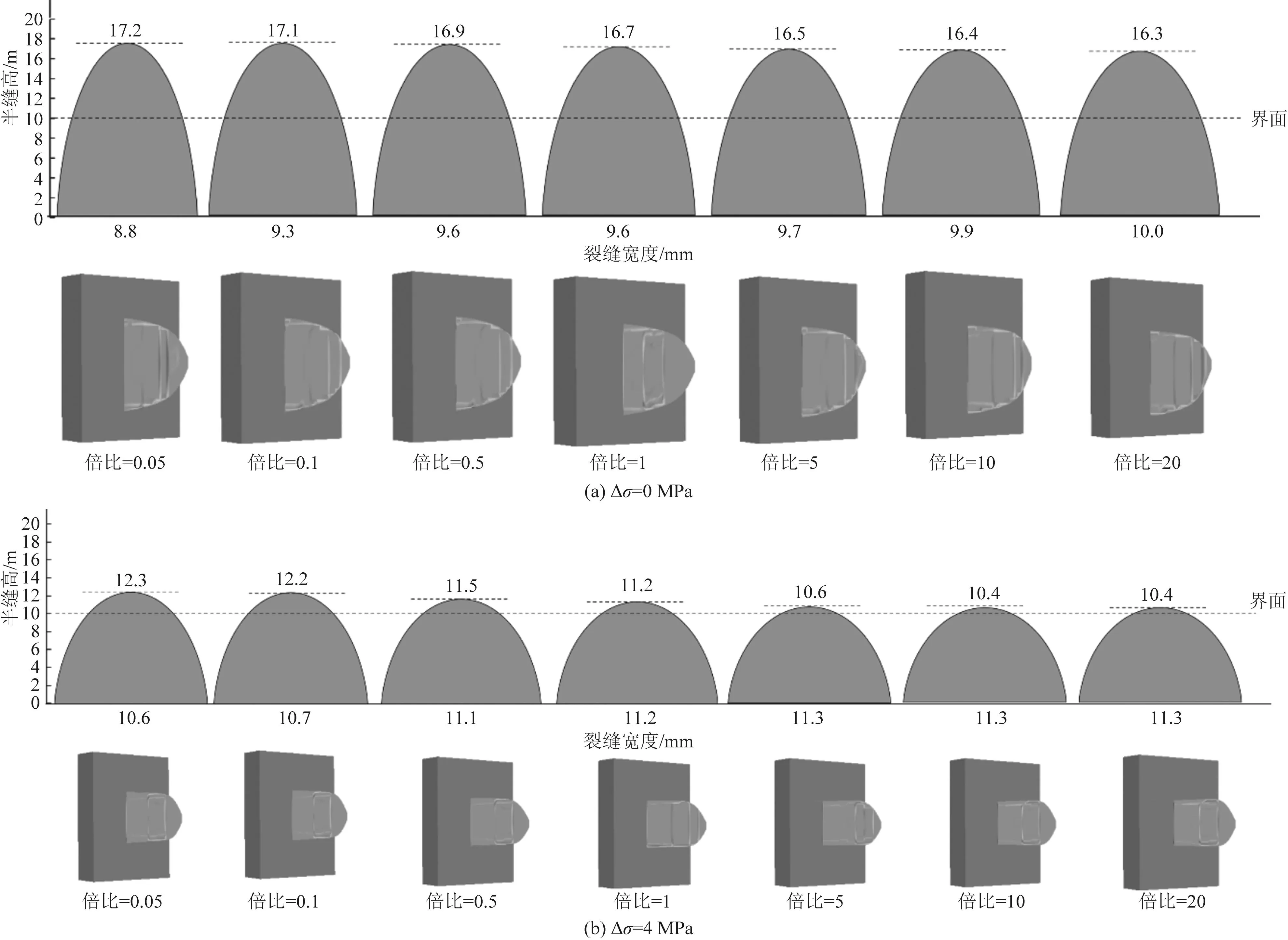
图7 不同应力差下杨氏模量倍比对裂缝高度的影响

绘制不同应力差下缝高、缝宽变化曲线和裂缝穿深变化幅度曲线(图8、图9)。由图8可以看出,在不同的储隔层应力差下缝高、缝宽的变化规律相似,随着杨氏模量倍比增大,即隔层杨氏模量越小,裂缝高度越小,缝宽越大。但储层在高模量和低模量下对缝高的影响程度不同(图9)。在储层为高模量时,即储层模量高于隔层模量时,裂缝穿深幅度均为负值,缝高均比无模量差时的缝高要小,此时裂缝的生长受到明显抑制,且缝高基本维持在一个定值。这是因为在层状地层中裂缝宽度不仅依赖于产层局部模量,也受到临近隔层模量的影响。当外部隔层的模量低于中间产层的模量,那么产层中的裂缝宽度会变得更宽,较宽的裂缝会对流体流动的阻力较小,从而导致流压较低。在相同应力差的条件下,净压力越低,产生的裂缝高度就越低;而在储层模量为低模量,即储层模量低于隔层模量时,裂缝穿深幅度均为正值,缝高均比无模量差时的缝高要大,缝高受到的抑制作用较弱。这是因为产层的裂缝宽度受限,所以缝中流体流压较高,得到的缝高也相对较高一些。另外,不同应力差下穿深变化的幅度也不相同。Δσ=0 MPa时,穿深变化幅度都在±10%以内,变化幅度较小,当模量倍比增大5倍时,穿深变化幅度仅-2.62%,当模量倍比减小5倍时,穿深变化幅度仅5.84%;而当Δσ=4 MPa时,穿深变化幅度在±100%以内,变化幅度较大,当模量倍比增大5倍时,穿深变化幅达度-48.94%,当模量倍比减小5倍时,穿深变化幅度达62.13%。

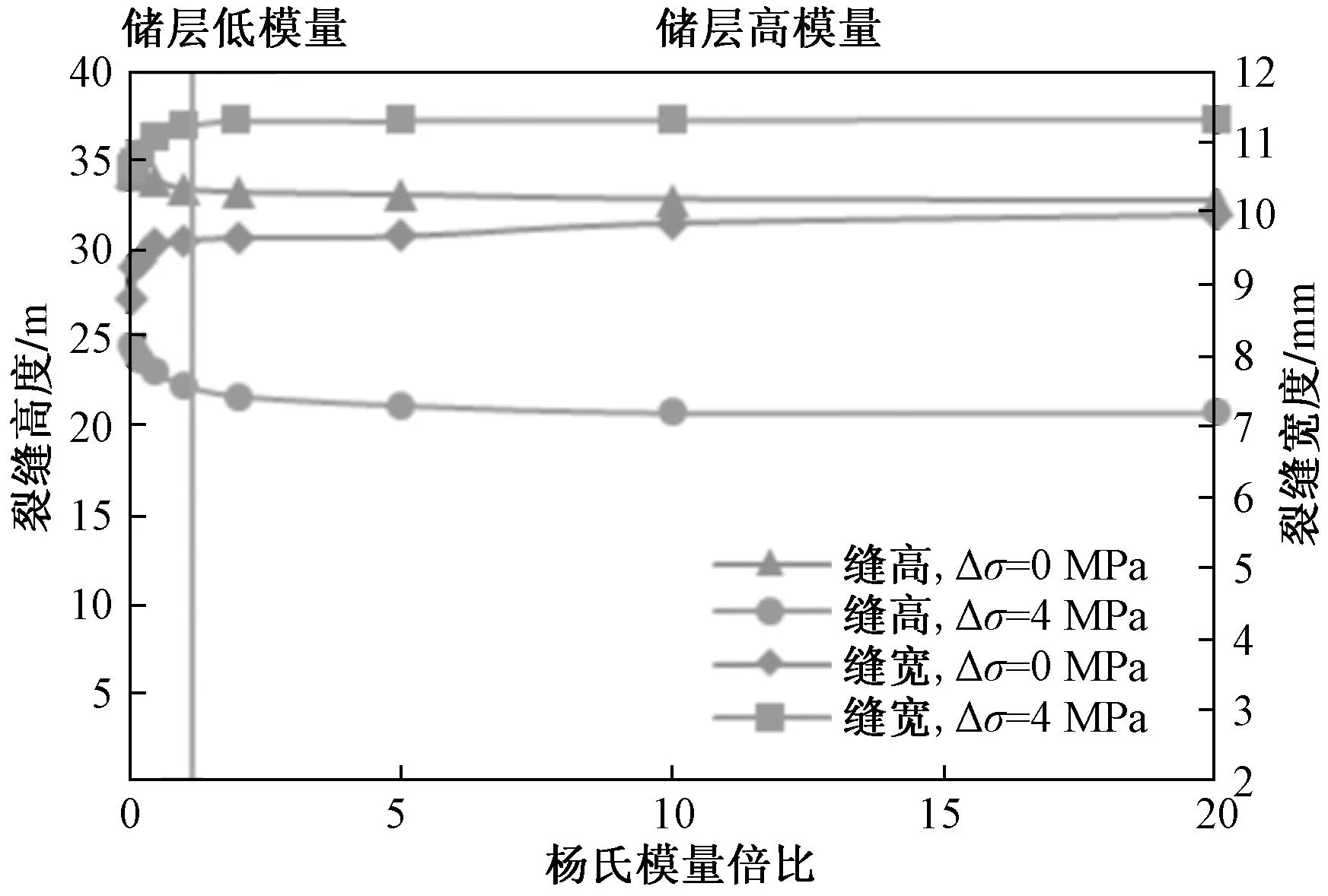
图8 不同杨氏模量倍比、不同应力差下裂缝高度和宽度变化曲线

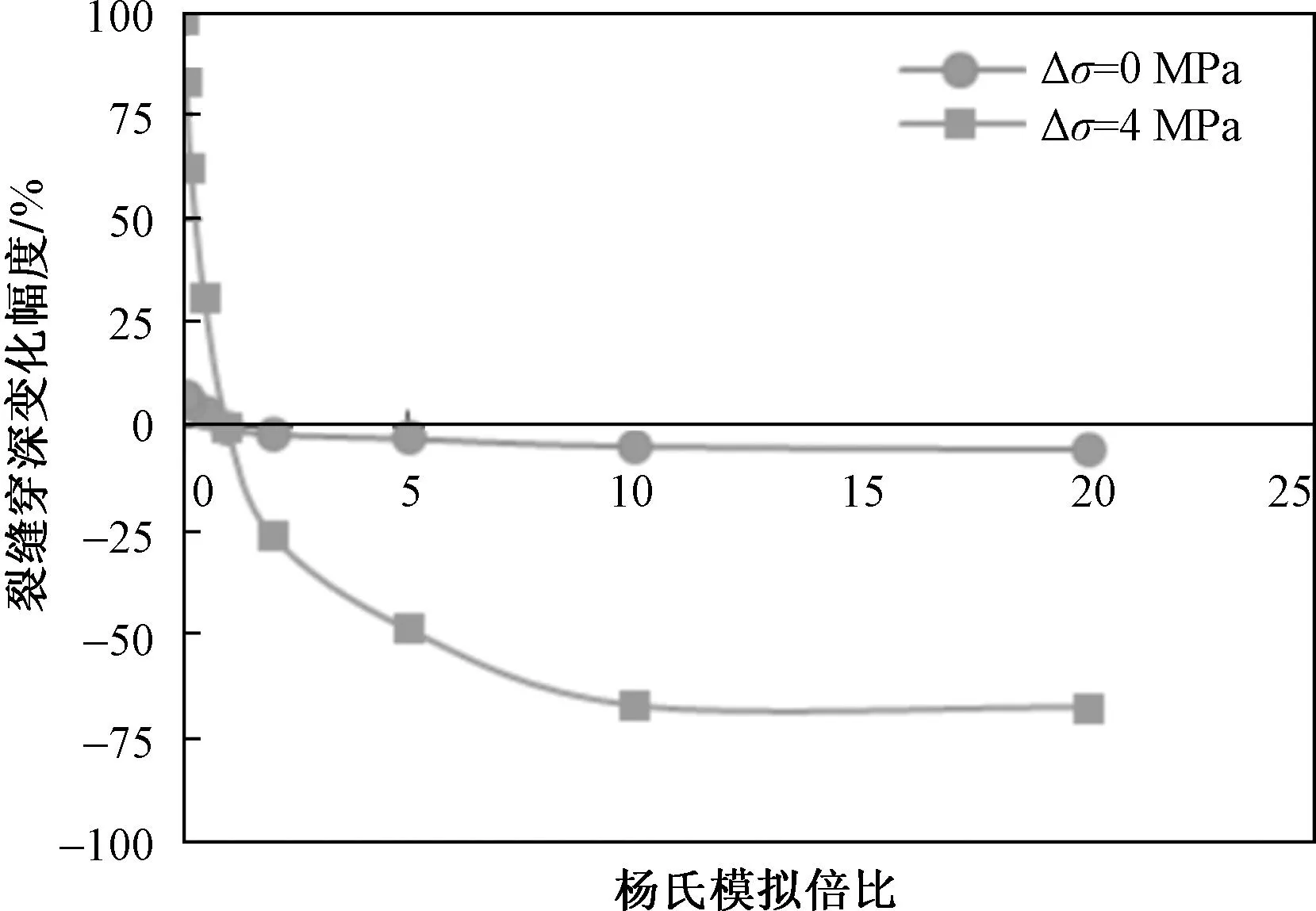
图9 不同杨氏模量倍比、不同应力差下裂缝穿深变化幅度曲线

研究结果表明,在不同的储隔层模量差下,其对缝高的控制规律并不完全相同。隔层低模量,缝高容易受到控制,同时隔层模量的变化对缝高的影响几乎不变;隔层高模量,缝高不易受到控制,隔层模量的变化对缝高的影响作用较大。但总体而言,在低应力差条件下,裂缝全部穿层,穿深均达到10 m以上,缝高不受限制。同时储隔层岩石模量的差异往往较小,无法达到成倍的差异,同时加上杨氏模量属于岩石力学参数无法改变,因此,依靠杨氏模量来限制缝高不太现实。

3.3 泊松比

泊松比是计算水力裂缝缝宽的必要参数。Perkins和Kern[30]假定岩石是弹性介质,具有脆性,裂缝面为椭圆形,从而得出缝宽公式为

(6)

式中:W为裂缝宽度,mm;v为泊松比;E为杨氏模量,GPa;pnet为裂缝中的净压力;hf为缝高。由式(6)看出,在缝宽一定的情况下,泊松比越大,缝高越大,但砂岩的泊松比范围一般分布在0.20～0.38,泥页岩泊松比一般分布范围为0.15～0.35,数值和变化范围较小,对缝高的影响程度有限。

为了进一步研究不同应力差下不同储隔层泊松比对缝高扩展的影响程度,保持其他参数不变,设置储层泊松比为0.28,隔层泊松比分别为0.15、0.20、0.25、0.30、0.35,其模拟结果见表2。

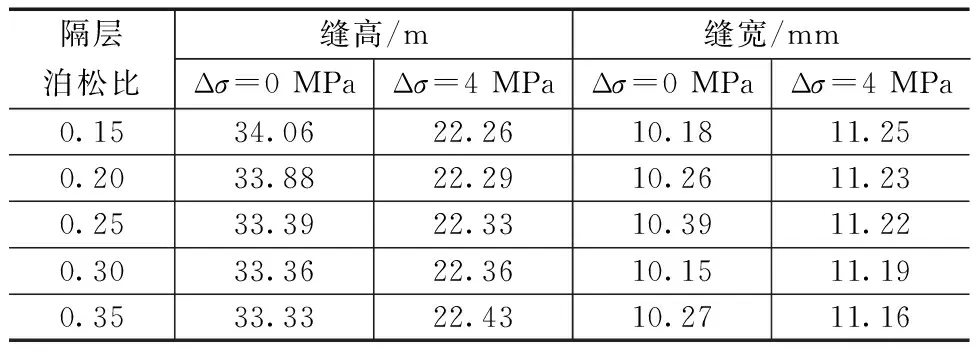
表2 不同泊松比、不同应力差下缝高和缝宽

绘制不同泊松比、不同应力差下裂缝高度和裂缝宽度变化曲线,如图10所示。不同应力差下不同隔层泊松比对裂缝高度和裂缝宽度影响很小,几乎可以忽略不计。但在应力差不同的情况下泊松比对缝高的影响规律不同。Δσ=0 MPa时,缝高与隔层泊松比呈负相关,缝高由泊松比0.15时的34.06 m减小至0.35时的33.33 m,减小0.73 m;Δσ=4 MPa时,缝高与隔层泊松比呈正相关,缝高由泊松比0.15时的22.26 m增加至0.35时的22.43 m,增加0.17 m。

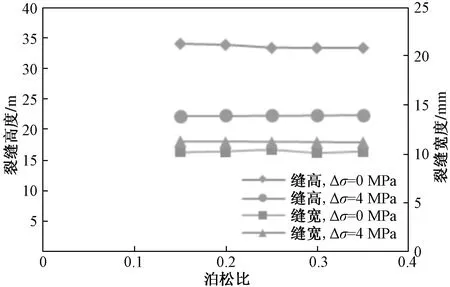
图10 不同泊松比、不同应力差下裂缝高度和宽度变化曲线

研究结果表明,泊松比对裂缝高度的影响非常微弱,甚至可以忽略不计。此外,通常情况下泊松比的数值较小。因此,依靠泊松比来限制裂缝高度的延伸同样不可靠。

4 施工参数对裂缝高度的影响

实际的压裂施工过程中,地质因素的对缝高控制作用无法人为进行干预和改变,但可以通过改变施工过程中的某些参数干预地质因素引起的缝高控制不确定性。

4.1 施工排量

施工排量是影响裂缝高度的一个重要因素,排量越大,裂缝越高。不同的气藏地层情况不同,排量对裂缝高度的影响程度也各有不同。根据目前研究表明,裂缝高度H和排量之间存以下关系[43]:

H=aebQ

(7)

式中:H为裂缝高度,m;Q为施工过程中平均排量,m3/min;a、b为经验常数。由式(7)可知,排量对缝高的影响并非是均衡的,在排量较小时,对缝高的影响很小。当排量增大到一定限度后,裂缝高度将急剧增大,有穿层危险。因此需要在施工过程中在保证达到设定目的缝长的基础上严格控制施工排量。

为了进一步研究施工排量对水力缝高的影响,改变施工排量,其他参数不变,设置单缝排量分别为1.0,2.0、3.0、4.0、5.0 m3/min,模拟结果如图11所示,在不同应力差下,随着施工排量的增加,裂缝形态由“短粗”型变为“细长”型。

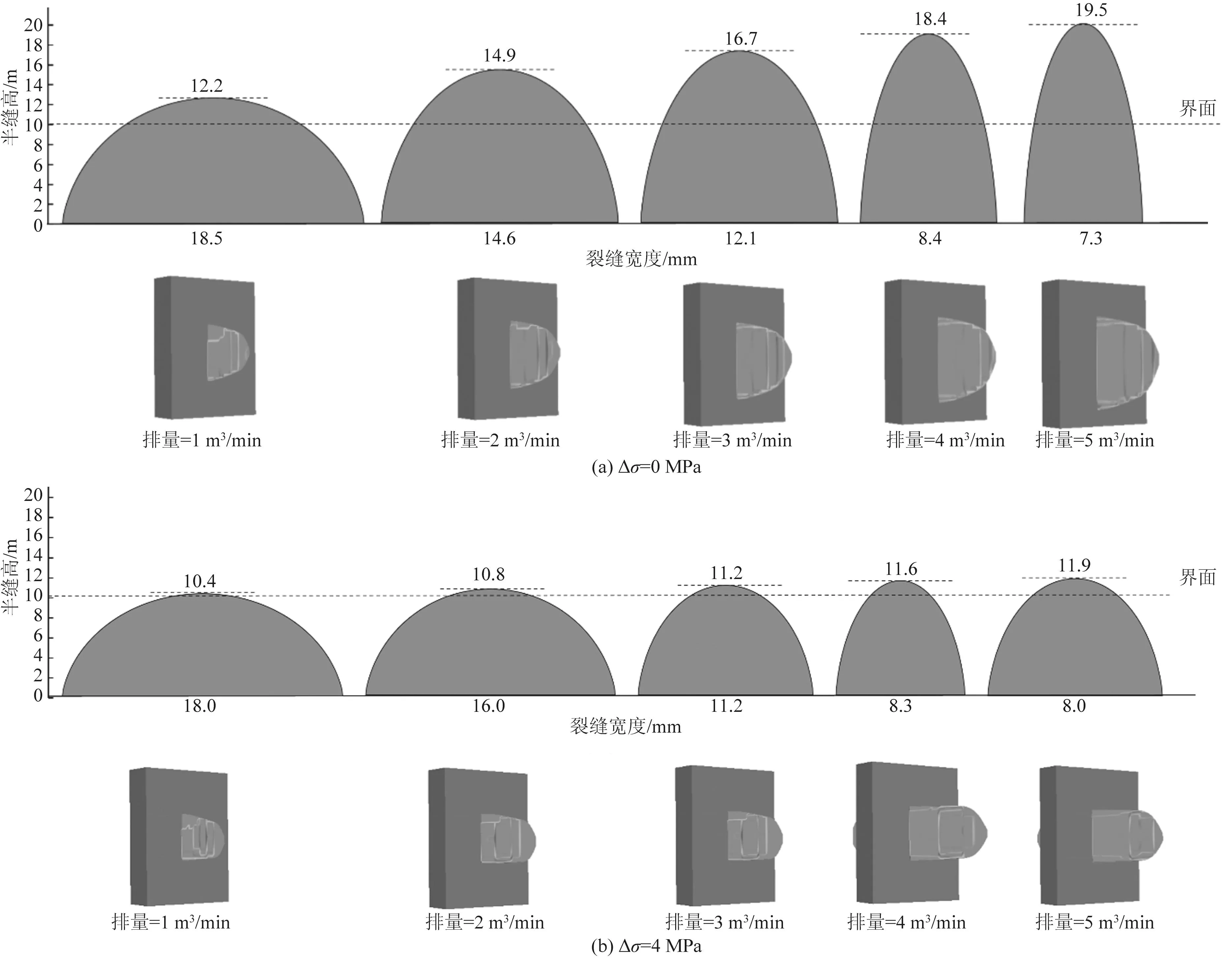
图11 不同应力差下排量对裂缝高度的影响

绘制不同应力差下缝高缝宽变化曲线和裂缝穿深变化幅度曲线,如图12和图13所示。缝高随着排量的增加接近线性增加,缝宽减小,而低应力差状态下(Δσ=0 MPa)排量对缝高的影响程度要大于高应力差状态(Δσ=4 MPa)。在同一排量下,应力差为0 MPa时的穿层深度约为应力差为4 MPa时的5倍。Δσ=0 MPa时,施工排量越大,穿层现象越明显,穿层深度由1 m3/min的4.35 m增加至5 m3/min的19.07 m,增加穿深达14.72 m;Δσ=4 MPa时,穿层深度由1 m3/min的0.87 m增加至5 m3/min时的3.84 m,穿层增加深度不足3 m。同时,从裂缝穿层深度的变化幅度来看,相较于排量为1 m3/min时的裂缝穿层深度,当排量增加至3 m3/min时,穿深变化幅度达200%,在排量达5 m3/min时,穿深变化幅度达340%。

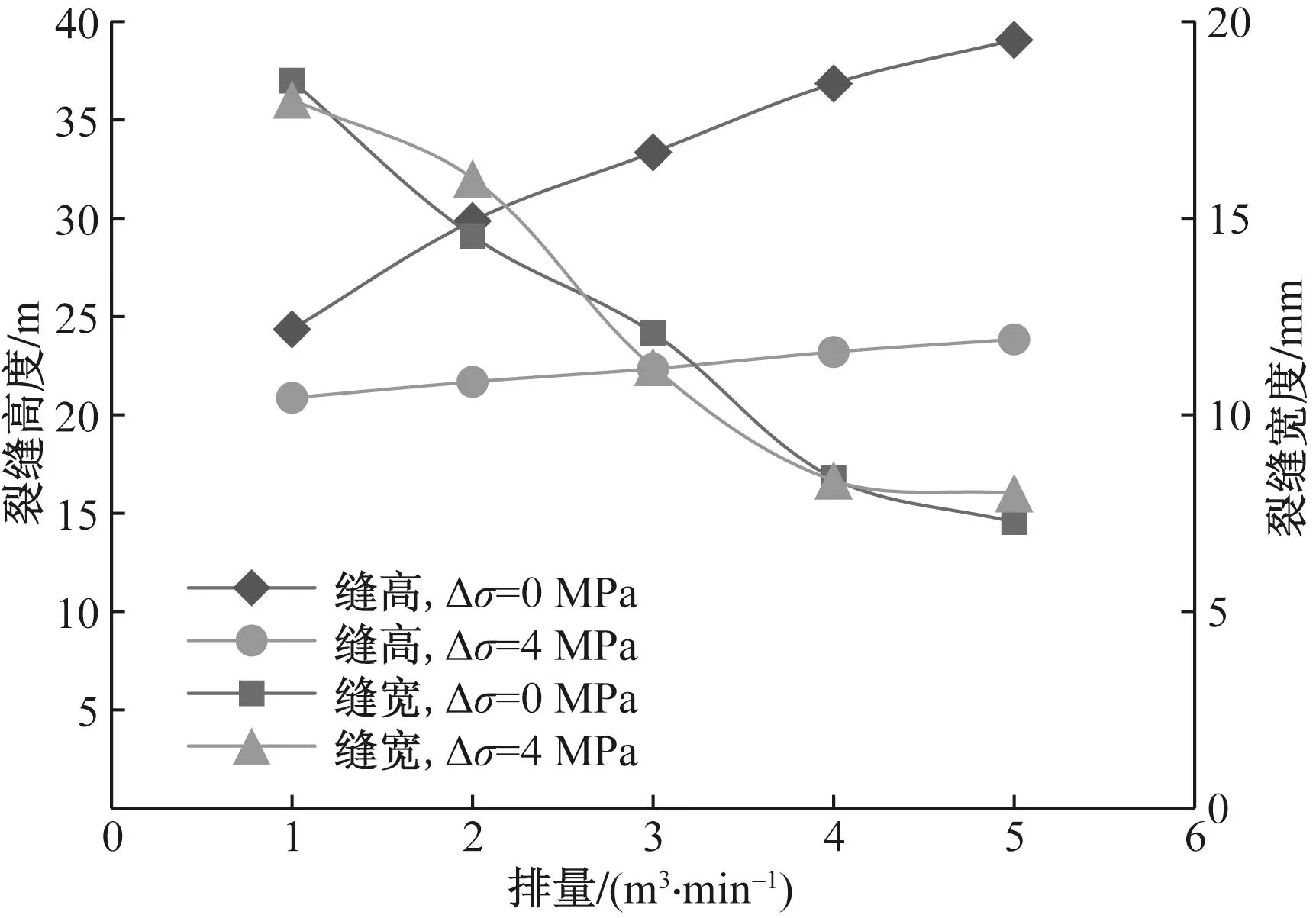
图12 不同应力差、不同排量下裂缝高度和宽度变化曲线

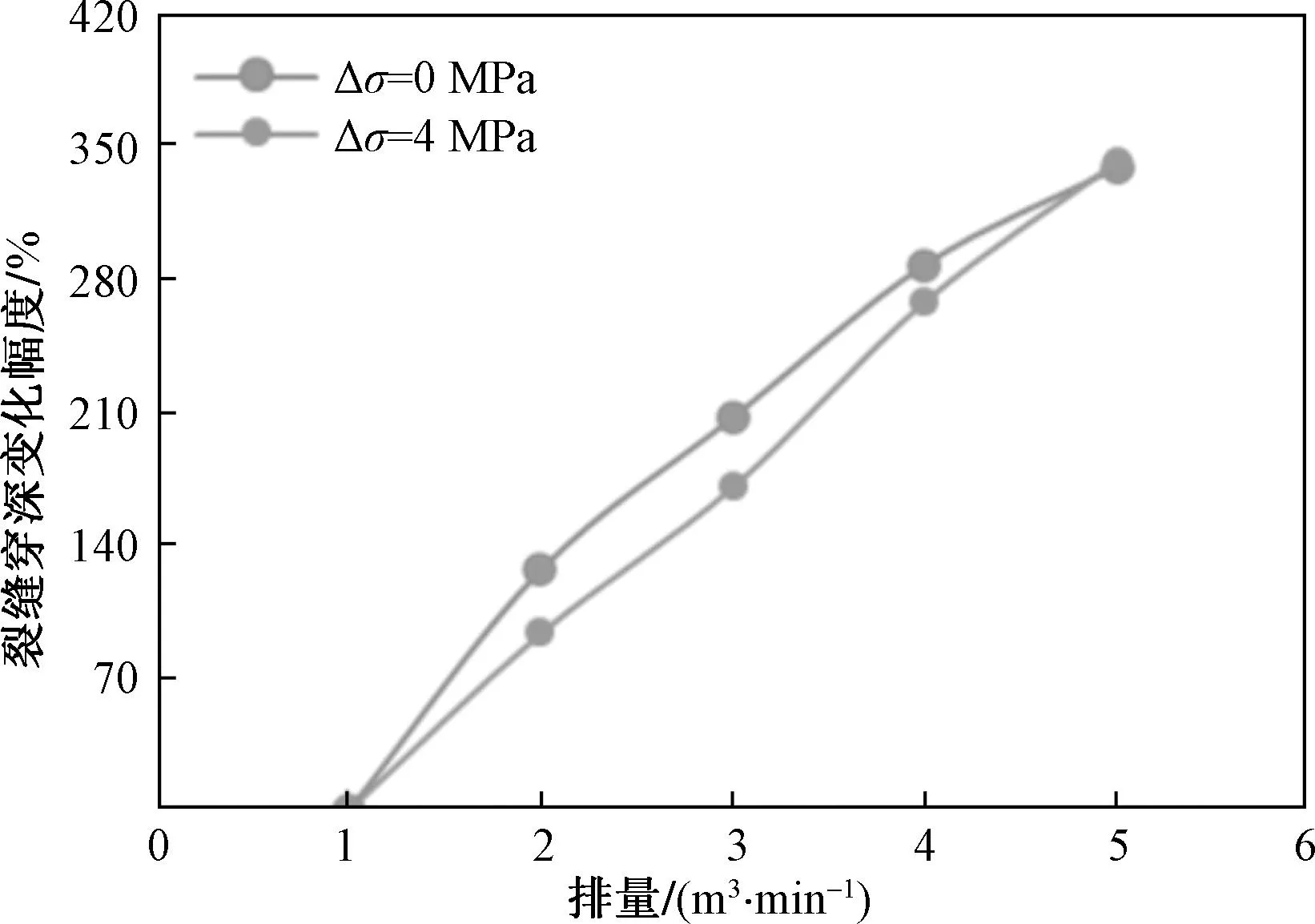
图13 不同应力差、不同排量下穿层深度变化幅度曲线

研究发现排量对缝高存在较大的影响,在高应力差下缝高受到排量的影响相对较小,即使在较高的排量下裂缝的延伸也受到较大的抑制,穿层深度相对较小;而在不存在隔层或储隔层应力差较小的情况下排量对缝高的影响程度更大,发生明显的穿层现象且几乎无法控制。因此,针对不同的储层情况设计合理的排量可有效地控制裂缝在高度上的延伸。

4.2 压裂液黏度

压裂液的黏度反映了压裂液的流动能力,随着压裂液黏度增大,其黏滞性越强,流动性能变差,易在封内憋压形成高压,从而使裂缝高度增加。同时压裂液黏度影响其摩阻、携砂能力、滤失速度和返排效率等,最终影响水力缝高。

为了进一步探究压裂液黏度对水力缝高的影响规律,在储隔层应力差分别为0 MPa和4 MPa的前提下,保持其他参数不变,设定压裂液黏度为1、10、30、50、100、200、400 mPa·s,其模拟结果如图14所示,在不同应力差下,随着压裂液黏度的增加,缝高越高,缝宽越小,裂缝形态由“短粗”型变为“细长”型。

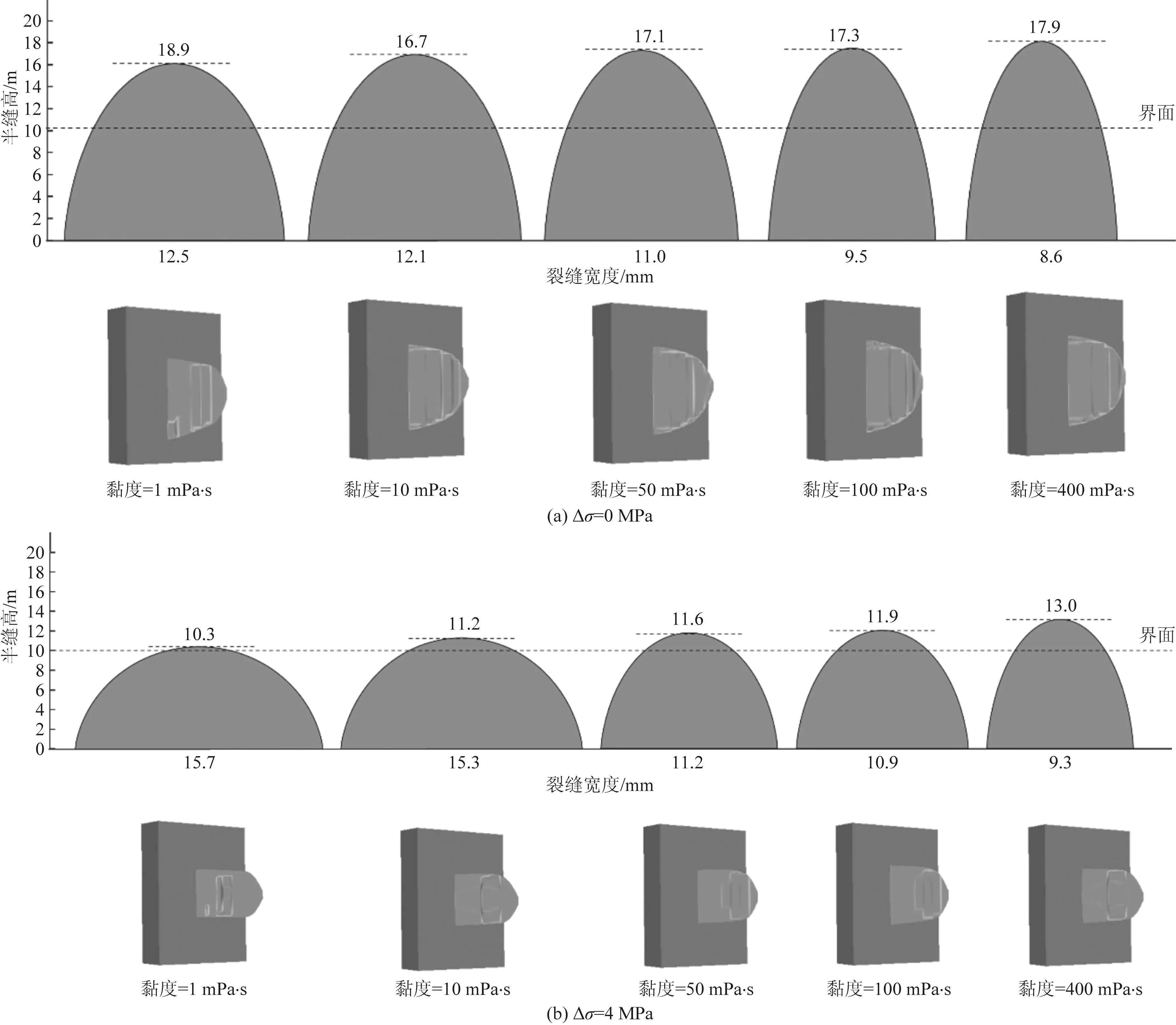
图14 不同应力差压裂液黏度对裂缝高度的影响

模拟结果(图15)表明,在低应力差状态(Δσ=0 MPa)下和高应力差状态下(Δσ=4 MPa),黏度对缝高的影响规律相似。压裂液黏度在1～50 mPa·s时对缝高的抑制作用较强,缝高相对较小,但缝高的变化幅度大;当压裂液黏度大于50 mPa·s之后,裂缝高度受到的抑制作用较小,缝高较高,此时缝高受黏度变化影响很小:Δσ=0 MPa时,在黏度为1 mPa·s时,穿层深度11.89 m,当黏度增加至50 mPa·s时穿层深度达14.24 m,缝高完全无法控制。但在Δσ=4 MPa时,黏度为1 mPa·s时穿层深度仅0.52 m,基本可视为无穿层,当黏度增大到50 mPa·s时,穿层深度为3.14 m,发生了明显的穿层现象,即使储隔层存在较高的应力差时,过高的压裂液黏度也会造成缝高的过度延伸。由图16看出,在Δσ=0 MPa时,虽然裂缝高度较大,穿层深度较大,但裂缝穿深的变化幅度却很小,从黏度1 mPa·s到100 mPa·s,穿深变化幅度仅23.3%。而Δσ=4 MPa时,裂缝高度相对而言更小,但裂缝穿深变化幅度很大,几乎成倍增加,从黏度1 mPa·s到100 mPa·s,穿深变化幅度达646%。

图15 不同应力差、不同黏度下裂缝高度和宽度变化曲线

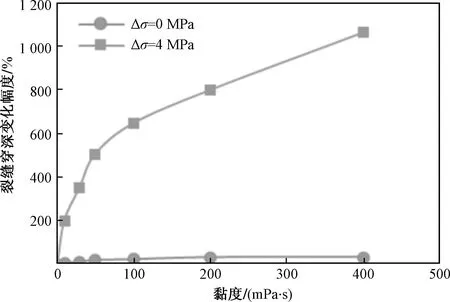
图16 不同应力差、不同黏度下穿层深度变化幅度曲线

研究发现压裂液黏度对最终裂缝高度有着较大的影响,特别是在储层不存在隔层或储隔层应力差较小的情况下影响程度更为明显。在压裂过程中,压裂液起着造缝和携砂的作用。通常情况下,使用的压裂液具有可变黏度,其黏度的变化范围较大。因此,在保证压裂液携砂能力的前提下,为了控制裂缝高度,需要严格控制和选择压裂液的黏度。

5 结论

基于多种裂缝扩展模型并结合现场的井温缝高测井数据,优选出了在缝高模拟上更为准确的P3D模型,并基于此模型研究了不同地质、工程因素对缝高扩展的影响规律,得出以下结论:

1)储隔层应力差是裂缝高度最关键的控制因素,直接决定了裂缝是否穿层。当应力差达到4 MPa时,穿层深度减小82.4%,当应力差达到6 MPa时能够将裂缝基本限制在储层内部。因此,建议在实际施工过程中尽量选择储隔层应力差大于4 MPa的致密砂岩气层进行压裂施工。

2)杨氏模量对缝高的影响作用相对较小,而且不同储隔层差异影响情况不相同。当隔层模量低于储层模量时,此时缝高较大,隔层模量的变化不会引起较大的缝高变化;在隔层模量高于储层模量时,此时缝高较小,模量的变化对缝高的变化影响较大。泊松比对压裂缝高几乎没有影响。

3)排量和压裂液黏度对缝高的影响仅次于应力差。在高应力差(Δσ=4 MPa)下,低排量1 m3/min时,裂缝穿层仅0.87 m,当排量增加至3 m3/min时,穿深达2.35 m,增加幅度达206.9%。同时相比于高应力差(Δσ=4 MPa),排量对无应力差(Δσ=0 MPa)条件下的裂缝高度影响程度更为明显。因此,建议在满足施工需求的基础上适当减小施工排量。

4)低黏度压裂液有利于控制裂缝高度。黏度在1～50 mPa·s缝高受到明显抑制,此时缝高受黏度影响变化幅度较大,当黏度超过50 mPa·s之后,缝高能够维持在一定高度,缝高较大但受黏度的影响变化幅度较小。因此,建议在满足造缝和携砂的前提下尽量选择低黏度压裂液进行施工。