考虑层理倾角的硬质砂岩力学行为及破裂响应特征

宋战平，刘洪珂，郑 方，程 昀，孙引浩，宋婉雪

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.陕西省岩土与地下空间工程重点实验室，陕西 西安 710055；3.西安建筑科技大学 隧道与地下结构工程研究所，陕西 西安 710055；4.盐城工学院土木工程学院，江苏 盐城 224051；5.中铁二十局集团第一工程有限公司，江苏 苏州 215000)

硬质砂岩作为典型的沉积岩，受沉积作用和成岩作用的影响，岩体内部存在大量的层理结构面[1]。随着岩土工程和采矿工程等领域深部开发战略的实施，复杂地质环境下层理结构面存在显著的角度差异，是导致岩石力学性能劣化甚至发生破裂的重要原因[2]，并且极易引发洞室围岩失稳破坏、隧道结构变形开裂等工程病害，直接影响工程建设质量和人民生命安全。因此，探究考虑层理倾角硬质砂岩的力学行为及破裂响应特征对于解决地下空间工程灾害问题具有重要的指导意义。

层理结构面的存在使得岩石力学性能显著降低，而层理倾角是影响含层理结构面岩石力学性能的重要因素。王聪聪等[3]开展不同层理倾角板岩的单轴压缩试验，发现层理倾角是单轴抗压强度、弹性模量和泊松比等力学参数呈现各向异性的重要原因。冯小磊等[4]通过干湿循环作用下页岩强度试验对不同层理倾角页岩的力学特征进行研究，总结抗剪强度指标与层理倾角之间的变化规律。李斌等[5]基于三点弯试验探究不同层理倾角砂岩断裂韧度的各向异性，并采用数值模拟方法揭示了层理倾角及层理结构面强度对岩石断裂力学行为的影响规律。Gao Quan 等[6]采用天然页岩，通过室内试验发现轴向垂直层理和轴向平行层理2 种页岩抗压强度和抗拉强度的差异性。

在含层理结构面岩石损伤破坏及机理研究方面，国内外众多专家学者同样展开了大量研究。赵振峰等[7]构建考虑流固耦合作用下的不同层理倾角页岩数值模型，准确模拟并预测岩石在渗流−应力耦合作用下的破裂过程和破坏模式，极大程度上为页岩气水力压裂开采提供理论依据。贾炳等[8]利用三轴压缩试验对煤岩加载过程中的声发射差异性进行分析，认为层理结构面可以显著影响岩石的变形破坏特征，集中体现在轴向垂直层理煤岩以整体变形破坏为主，而轴向平行层理煤岩以局部变形破坏为主。H.Niandou 等[9]基于三轴压缩试验和循环加卸载试验对含层理结构面Tournemire 页岩的弹性响应和塑性变形进行各向异性研究，发现含层理结构面岩石的破坏模式与加载方向和围压大小有关。

综上所述，目前关于含层理结构面岩石的力学性能及损伤破坏研究已经取得一定有益成果，但是考虑层理倾角的硬质砂岩力学行为及破裂响应特征尚不明确，有待进一步研究。因此，笔者基于不同层理倾角硬质砂岩的单轴压缩试验，一方面探究层理倾角影响下硬质砂岩的应力−应变关系和力学特征的各向异性，另一方面揭示硬质砂岩的宏观破坏模式及损伤破坏过程中的碎块分形特征，以期为开展不同层理倾角岩石的力学行为及破裂响应特征研究提供理论依据与指导。

1 试验材料与试验方案

1.1 试验砂岩

试验岩样选取四川成都地区的层状硬质砂岩，平均密度约为2.47 g/cm3，单轴饱和抗压强度大于30 MPa，外观呈青灰色且无明显的颜色变化，层理天然匀称、发育显著，层理结构面间距为1～2 mm，无明显缺陷。通过X 射线衍射(XRD)测定硬质砂岩的矿物组成，具体为：斜长石(质量分数71%，下同)、石英(10%)、方解石(4%)、蛭石(4%)、钾长石(3%)、赤铁矿(2%)、闪石(2%)、蛇纹石(2%)、绿泥石(1%) 及其他成分(1%)。同时，利用扫描电子显微镜(SEM)对硬质砂岩的层理结构面进行观察，分别从放大倍数为500 倍和2 000 倍观察其微观结构(图1)。晶体颗粒表面光滑无裂隙、结构较为完整、排列相对紧密，颗粒之间通过胶结物黏结形成骨架，而胶结物呈絮状分布，微裂隙发育显著，这是在微观层面上引起硬质砂岩力学性能劣化的原因。

1.2 岩样制备

考虑到沉积岩独特的成岩特性赋予其典型的层理特征，为深入探究硬质砂岩力学特征的各向异性，本次试验分别制备了5 种不同层理倾角下(0°、22.5°、45.0°、67.5°、90.0°)直径50 mm、高100 mm 的标准圆柱状硬质砂岩试样(图2)，其中层理倾角是指层理结构面与水平面之间的夹角。

岩样具体制备过程如下：步骤Ⅰ，准备新鲜完整岩块；

步骤Ⅱ，通过切石机将岩块切割成具有水平层理的长方体状岩块；步骤Ⅲ，利用钻石机按照不同的钻取方向进行取心；步骤Ⅳ，取心成功后先用切石机将2 个端面切割平整，再经磨石机打磨抛光，从而得到试验所需岩样。端面的不平行度和不垂直度严格符合GB/T 50266−2013《工程岩体试验方法标准》[10]的要求，分别控制在≤0.05 mm 和≤0.25°。

1.3 试验设备

本试验在西安建筑科技大学岩土与地下空间工程重点实验室完成，采用WAW-600B 型微机控制电液伺服岩石拉压试验机，该设备主要由试验机主机(压缩夹具、高精度负荷传感器和伺服控制专用油源)和PC机控制系统组成，如图3 所示。该试验机具有应力控制和应变控制2 种加载方式，可提供的最大试验力为600 kN，试验力分辨率为0.10 kN，试验力误差在±1%以内。

1.4 试验方案

本试验主要研究层理倾角对硬质砂岩力学行为和破裂响应特征的影响，基于此试验目的，对5 种不同层理倾角的硬质砂岩试样进行单轴压缩试验。

试验分为以下3 步进行：

(1)将制备好的岩样依次进行质量及密度测试，剔除破损、质量和密度异常的岩样。将测试结果合格的岩样根据层理倾角分为5 组，每组设置2 个平行试验，一共10 个试样，分别进行编号(表1)。

表1 硬质砂岩单轴压缩试验方案Table 1 Uniaxial compression test scheme for hard sandstone samples

(2)为消除端面摩阻力的影响，在岩样两端涂抹润滑剂。正式试验之前进行轴向荷载为0.20 kN 的初始预压，确保岩样同试验机压缩夹具有效接触。受预压荷载的影响，应变初始值约为0[11]。

(3)单轴压缩试验全程采用应力控制的方式进行加载，以1.5 MPa/s 的加载速率至岩样破坏，应力−应变曲线由PC 机控制系统自动采集。本试验将选取2个平行试验中最具代表性的试验结果作为最终试验结果。

2 力学行为分析

2.1 应力−应变曲线

单轴压缩下不同层理倾角硬质砂岩的应力−应变曲线。

如图4 所示。从图中可以看出，应力−应变曲线在整体形态分布方面具有相似性，但由于层理倾角的不同，局部表现出一定的差异性。硬质砂岩的应力−应变曲线可近似分成4 个区段，分别为压密阶段、弹性阶段、塑性阶段和脆性阶段。

图4 不同层理倾角硬质砂岩的应力−应变曲线Fig.4 Stress-strain curves of hard sandstones with different bedding dip angles

1)压密阶段Ⅰ(OA 段)

该阶段持续时间占全过程的10%～14%，其应力−应变曲线近似呈向上弯曲增长趋势，应力最大值分布在10 MPa 左右，应变最大值分布在0.005 左右。应力−应变曲线的斜率随着应力的增加表现出先缓慢增长后急速增长的特征，该特征随着层理倾角的增大越发突出，在倾角为67.5°和90.0°时表现得尤为明显。分析原因认为，压密阶段是由于细微裂隙受压闭合造成的，加载初期变形较大，曲线较为平缓、增速缓慢。倾角较大时，原生裂隙闭合和层理面微滑移抵消导致岩石的刚度增加，曲线陡峭增长。

2)弹性阶段Ⅱ(AC 段)

弹性阶段(AC 段)可分为弹性变形阶段(AB 段)和裂纹稳定扩展阶段(BC 段)[12]，该阶段持续时间占全过程的25%～40%，其应力−应变关系近似于一条直线。倾角为0°时出现应力最大值64 MPa，倾角67.5°时出现应力最小值32 MPa，前者约为后者的2 倍，说明层理倾角的变化对处于弹性阶段岩石的强度存在显著的影响。岩石进入弹性变形阶段，内部裂隙闭合完全，表面基本完整，无明显裂纹。随着荷载的继续增加，岩石进入裂纹稳定扩展阶段，原生裂隙开始扩展，表面产生细微裂纹并伴随有破裂声，新裂纹的起裂方向与最大压应力的作用方向保持一致[13]，此时的应力−应变曲线出现小幅度下跌。

3)塑性阶段Ⅲ(CD 段)

该阶段处于裂纹非稳定扩展阶段，持续时间占全过程的10%～25%。随着荷载的进一步增加，岩样表面出现明显扩张裂纹并伴随有显著破裂声，倾角为45.0°、67.5°的岩样发生碎片飞溅，体积由压缩转为扩容，应力达到峰值强度。同时，该阶段的应力−应变曲线随层理倾角的变化表现出一定差异，可概括为两类变化[14]。倾角较小时(0°、22.5°、45.0°)，峰值附近曲线无明显的上下波动，近似为单峰曲线；倾角较大时(67.5°、90.0°)，峰值附近曲线呈锯齿状变化，近似为多峰曲线。分析原因认为，倾角较小时，岩样破坏受层理面影响较小，表现为脆性破坏；倾角较大时，层理面对岩样的破坏起主导作用，因此在荷载作用下易发生层理面滑移，造成应力跌落，从而导致曲线的波动。

4)脆性阶段Ⅳ(DE 段)

该阶段处于脆性破坏阶段，由于本试验所使用的压力机并非变形小的刚性压力机[15]，故岩样在峰值处突然破坏，发生急骤变形并伴随有显著爆鸣声，碎片猛烈飞溅。应力−应变曲线骤然下降，且产生回弹现象，倾角为22.5°、45.0°、90.0°岩样的回弹现象特别明显，这说明岩样在破坏后并没有完全失稳，仍具有一定的刚度和承载能力。

通过对单轴压缩下不同层理倾角硬质砂岩的应力−应变曲线进行对比分析，认为层理结构面的存在增加了硬质砂岩的非均质性，降低了其整体强度，并且层理倾角极易改变硬质砂岩内部的应力状态，从而导致加载过程中应力−应变曲线呈现出差异性，主要体现在以下2 个方面。层理倾角的增加，导致硬质砂岩强度的劣化程度提高，尤其倾角为67.5°时，劣化程度最高。分析原因认为，层理结构面晶体颗粒之间的胶结能力较差，降低了硬质砂岩抵抗变形破坏的能力。倾角为0°时，即轴向荷载与层理结构面相互垂直，对硬质砂岩的强度影响较小；倾角为67.5°时，基本达到了理论剪切破坏面角度(45.0°+φ/2)，φ为岩石的内摩擦角，此时发生层理结构面滑移，对硬质砂岩的强度影响较大。倾角为0°和90.0°硬质砂岩的应力−应变曲线峰值滞后性更加明显。分析原因认为，倾角为0°和90.0°时，轴向荷载与层理结构面相互垂直、平行，此时硬质砂岩可近似视为横观各向同性体。加载过程中，大量弹性能在硬质砂岩内部聚集，能量积聚率较大，表现为在应变为0.013 附近处发生失稳破坏。而其余倾角的硬质砂岩由于层理结构面造成损伤，能量积聚率较小，表现为在应变为0.01 附近处发生失稳破坏。

2.2 峰值应力、应变

为了量化研究层理倾角对硬质砂岩力学性能的影响，根据图4 中应力−应变曲线得到不同层理倾角硬质砂岩的峰值应力σd和峰值应变εd，分析两者同层理倾角的数值关系对于预测岩石破坏具有重要的参考意义。图5 为硬质砂岩的峰值应力和峰值应变与层理倾角的变化关系曲线。如图所示，峰值应力和峰值应变随着层理倾角的增大均近似表现为先减小后增大的类“W”形变化趋势。

从小学数学当前实际的教学情况来看，教学效果并不是十分理想，之所以会出现这种情况，主要是因为一些教师仍然在使用比较传统的教学方法，而这种方式最大的弊端就是无法激发学生的学习热情，所以为了改变这种情况，教师首先应该做的就是激发学生学习热情。因此，在启发式教学中，教师可以从学生的生活出发，利用学生比较熟悉的生活事物或生活场景来创设教学情境，这样一来，可以使教学内容的趣味性增加，从而更好地调动学生的学习热情，只有这样，才能为启发式教学的顺利展开奠定比较好的基础。

图5 力学参数与层理倾角的变化关系曲线Fig.5 Curves showing relationships between mechanical parameters and the bedding dip angle

倾角为0°、22.5°、45.0°、67.5°、90.0°所对应的峰值应力σd依次为75.91、64.83、64.32、46.25、59.65 MPa，峰值应力σd在倾角为0°和67.5°时分别达到最大值75.91 MPa 和最小值46.25 MPa，同倾角0°相比，22.5°、45.0°、67.5°、90.0°所对应的峰值应力σd分别下降了15%、15%、39%、21%。分析原因认为，倾角为0°时，轴向荷载与层理结构面相互垂直，岩石破坏主要取决于颗粒间的摩擦强度和黏聚强度；倾角大于0°时，出现层理结构面滑移现象，且岩石存在最不利层理结构面。在达到最不利层理结构面前后，岩石破坏趋向于沿层理结构面发生滑移，在达到最不利层理结构面时，岩石在最不利层理结构面发生滑移剪切破坏，峰值应力下降甚至达到最小值。

倾角为0°、22.5°、45.0°、67.5°、90.0°所对应的峰值应变εd依次为12.89×10−3、10.24×10−3、10.43×10−3、9.80×10−3、13.56×10−3，峰值应变εd在倾角为90.0°、0°和67.5°时分别达到最大值13.56×10−3、次大值12.89×10−3和最小值9.80×10−3，同倾角0°相比，22.5°、45.0°、67.5°所对应的峰值应变εd分别下降了21%、19%、24%。分析原因认为，倾角为90.0°的岩石产生压杆效应，趋向于劈裂破坏；倾角为67.5°的岩石发生最不利层理结构面滑移剪切破坏，峰值应变同峰值应力达到最小值。此外，层理倾角对硬质砂岩应变的影响变化均匀，削弱程度在20%左右，即层理倾角对硬质砂岩应力的影响同比应变更为显著。

2.3 各向异性特征

通过2.2 节分析发现，层理倾角改变影响峰值应力和峰值应变的大小，说明硬质砂岩具有各向异性特征，弹性模量E常用来描述岩石的变形特性，各向异性可能同样对其具有影响。为了量化各向异性对岩石力学参数的影响，引入各向异性度[16]的概念，其表达式为：

式中：k为各向异性度；Pmax为峰值应力最大值、峰值应变最大值、弹性模量最大值等参数；Pmin为峰值应力最小值、峰值应变最小值、弹性模量最小值等参数。

非线性弹性模量E的精确取值较为困难，本文将应力−应变曲线上原点与某点(峰值应力的50%)连接直线的斜率作为弹性模量。根据相关曲线和公式计算得到不同层理倾角硬质砂岩的峰值应力σd、峰值应变εd和弹性模量E的各向异性度。以峰值应力、峰值应变和弹性模量计算得到的各向异性度分别为1.64、1.38 和1.32，受层理倾角的影响，硬质砂岩表现出一定的各向异性特征，但各向异性特征并不明显，经判断硬质砂岩属于低各向异性岩石。由于以弹性模量计算得到的各向异性度几乎不受试验类型的影响，使用弹性模量作为岩石各向异性度的衡量标准[17]，峰值应变的各向异性度略高于弹性模量，而峰值应力的各向异性度同比弹性模量增长24%，说明峰值应力的各向异性特征较峰值应变和弹性模量明显，层理倾角对峰值应力的扰动偏大，这与文献[18]未施加围压状态下的研究情况基本一致。

3 破裂响应特征分析

3.1 宏观破坏模式

单轴压缩下由于岩石无侧向压力的约束，其破坏模式较为复杂。根据大量的试验和观察证明，岩石在单轴压缩条件下的破坏模式大致分为X 型共轭剪切破坏、单斜面剪切破坏和张拉破坏3 种类型[19]。影响破坏模式的因素包括矿物成分、层理特征、加压方式等，本文只探究单轴压缩条件和层理倾角变化对岩石破坏模式的影响。

参照上文标准，同样选取2 个平行试验中最具代表性的试验结果作为最终试验结果。图6 是不同层理倾角的硬质砂岩在单轴压缩条件下的宏观破坏模式图。如图所示，硬质砂岩的破坏模式受各向异性的影响，但同层理倾角之间表现出一定的规律性。倾角为0°时，岩样出现典型的X 型共轭剪切裂纹和单斜面剪切裂纹，2 种裂纹发生贯通，局部出现横向张拉裂纹，硬质砂岩主要发生剪切破坏；倾角为22.5°时，岩样出现未贯通的X 型共轭剪切裂纹和贯通的单斜面剪切裂纹，且形成一条主剪切面，局部出现少量劈裂裂纹，硬质砂岩以剪切破坏为主；倾角为45.0°时，岩样表面岩体与岩心发生脱离，表面岩体中部断折，岩心形成一条贯通的主断裂面，硬质砂岩破坏模式复杂，表现为剪切张拉复合破坏；倾角为67.5°时，岩样出现2 条沿着层理结构面方向的主剪切面且发生滑移，这与理论剪切破坏面角度(45.0°+φ/2)基本一致，底部出现细密网状裂纹，此时硬质砂岩发生层理结构面剪切破坏；倾角为90.0°时，岩样出现多条贯通的竖向裂纹，局部伴随少量断折裂纹，硬质砂岩发生劈裂破坏。

图6 硬质砂岩样宏观破坏模式Fig.6 Macroscopic failure modes of hard sandstone samples

3.2 碎块质量特征

单轴压缩下硬质砂岩试样破坏，产生不同尺寸和质量的碎块，其呈现出一定的分布规律，即碎块分布特征。为进一步研究碎块质量分布特征，采用筛分法[20]对硬质砂岩碎块进行分类统计，根据所用的不同孔径石筛将碎块分为9 个分布区间(表2)。按照相关分类标准，将分布区间r≤5 mm、5 mm＜r≤20 mm、20 mm＜r≤50 mm、r＞50 mm 的碎块分别划分到细粒、细块、中块和粗块类别，其中，分布区间为20 mm＜r≤40 mm的碎块为主碎块。不同层理倾角硬质砂岩碎块的分布区间及质量百分比见表2，“−”表示该分布区间未出现相应尺寸的碎块，并根据表2 中的数据绘制硬质砂岩碎块的质量分布直方图，如图7 所示。

表2 硬质砂岩碎块的分布区间及质量百分比Table 2 Size distributions and mass percentages of hard sandstone fragments

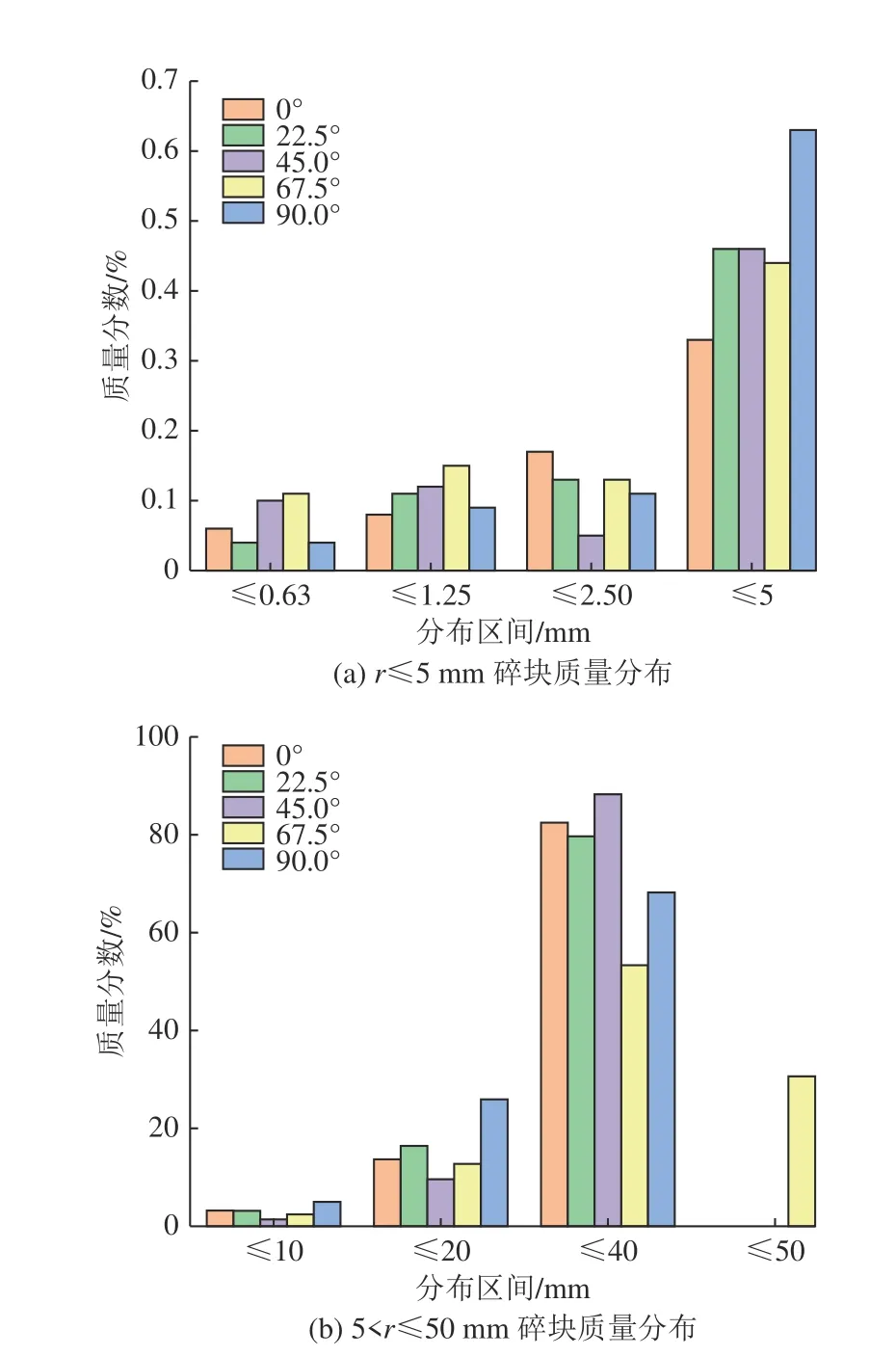
图7 硬质砂岩碎块质量分布直方图Fig.7 Histograms showing the mass percentages of hard sandstone fragments

由表2 和图7 可知，不同层理倾角的硬质砂岩试样在单轴压缩条件下破坏形成的碎块以中块、细块和细粒为主，未出现尺寸＞50 mm 的粗块。倾角为67.5°的硬质砂岩出现尺寸＞40 mm 且≤50 mm 的碎块，其余倾角的硬质砂岩碎块尺寸均≤40 mm。其中，分布区间20 mm＜r≤40 mm 的主碎块质量占碎块总质量的53.34%～88.26%，即中块作为岩石碎裂后的主要碎块类别。当倾角从0°增加至90.0°时，分布区间r≤5 mm的碎块质量小于3 g，质量分数小于1%，相同分布区间的中块和细块碎块的质量分数差异性明显大于细粒碎块，说明层理倾角对细粒碎块的质量分布影响较小，这也与岩石的宏观破坏模式有关。

3.3 碎块分形特征

分形理论[21-22]研究岩石碎块的分布规律，在岩石破碎领域得到广泛应用。本文以不同层理倾角的硬质砂岩碎块为研究对象，采用碎块的质量−粒径分形计算方法[23]进行分形特征研究，其分布计算方程[24]如下：

式中：r为岩石碎块的特征粒径，即各分布区间的筛分尺寸；M(r)为等效粒径R小于特征粒径r的岩石碎块质量；MT为岩石碎块的总质量；Dr为岩石碎块的分形维数。

岩石由整体破坏为碎块的过程中，其等效粒径R存在以下等式关系：

式中：V为岩石碎块的等效体积；l、d、h分别为岩石碎块的等效长度、宽度、高度。

对式(2)两边取自然对数可得：

由式(4)可知，双对数 ln[M(r)/MT] 与 lnr存在线性关系，3−Dr为双对数坐标下的线性斜率值，线性关系越明显，则岩石碎块的分形特征越好。因此，利用单轴压缩试验并通过筛分法可以统计不同分布区间岩石碎块的质量、粒径等物理参数，绘制质量与粒径关系曲线，通过数值回归可确定岩石碎块的分形维数。这里根据上文统计结果进行数值拟合，绘制回归关系，如图8 所示。

图8 硬质砂岩碎块质量与粒径回归曲线Fig.8 Regression curves of the mass and particle size of hard sandstone fragments

由图8 可知，本文所研究的硬质砂岩碎块质量与粒径回归曲线的相关系数R2高达0.84～0.96，线性相关性明显，即分形特征良好，表明不同层理倾角的硬质砂岩破碎具有良好的自相似性。倾角为0°、22.5°、45.0°、67.5°、90.0°的硬质砂岩碎块的回归曲线斜率分别为1.79、1.85、1.68、1.53、1.92，曲线斜率呈现出先减小后增大的趋势，最小斜率出现在倾角67.5°的数据，和上文研究结果相互印证。分形维数可以定量表征岩石的破碎程度，分形维数值越大，岩石的破碎程度越高。倾角为0°、22.5°、45.0°、67.5°、90.0°的硬质砂岩碎块的分形维数分别为1.21、1.15、1.32、1.47、1.08，分形维数值均位于1～2，且在倾角为67.5°时达到最大值，说明大尺寸分布区间的碎块所占比例较大。层理倾角与岩石破裂具有交互的应力响应，应力协调和损伤积累较为充分，从而导致岩石更容易发生失稳和破裂。

4 结论

a.层理倾角较小的硬质砂岩应力−应变曲线表现出单峰的变化规律，而层理倾角较大的硬质砂岩应力−应变曲线表现出多峰的变化规律；层理倾角对硬质砂岩应力的影响明显大于应变，峰值应力σd和峰值应变εd均在最不利层理结构面达到最小值，且硬质砂岩表现出低各向异性特征。

b.层理倾角对硬质砂岩的破坏模式具有显著影响，随着层理倾角的增大，硬质砂岩呈现出剪切破坏−剪切张拉复合破坏−层理结构面剪切破坏−劈裂破坏的损伤破坏演化规律。

c.研究层理倾角对含层理结构面岩石的力学行为及破裂响应特征的影响，对实现地下空间工程灾害防治具有一定的理论价值。层理倾向同样影响含层理结构面岩石的力学性能，建议下一步综合考虑层理倾角和层理倾向的变化以及渗透水压力作用下的含层理结构面岩石在三轴压缩条件下的变形规律研究工作。