铬污染场迁移特性及双频激电监测技术研究

韦凯耀，刘志民，梁 晨，张 杰，马 强

(1.河北工程大学 机械与装备工程学院，河北 邯郸 056038；2.河北省冀南新区现代装备制造协同创新中心，河北 邯郸 056038)

随着我国经济和社会的快速发展，土壤污染问题日益严重，被铬、镉、铅、铜、锌和镍等重金属污染的土壤占82.8%，其中铬(Cr) 超标率则达到了1.1%[1]。铬元素在土壤中有9 种价态，但主要以三价和六价2种价态稳定存在，三价和六价铬都对人体有害，六价铬毒性是三价铬的100 倍。六价铬污染能够改变微生物群落的构造[2]，是强致突变物质，当人类食用了含有六价铬的动植物，会引起皮肤刺激[3]、过敏性皮炎[4]、DNA 损伤[5]，严重的还会引起癌症[6]。土壤质量问题是关系国民经济可持续发展和社会全面进步的战略性问题，“十三五”期间，国家加大污染整治力度，先后出台相关文件《土壤污染防治行动计划》《“十三五”生态环境保护规划》，大力加强环境保护。为此，研究和开发先进有效的铬重金属土壤污染的源头预防、污染区域检测与修复技术势在必行。

目前常用的实验室土壤重金属监测方法有异位和原位监测法[7]，前者监测成本高、采样制样复杂、费时费力且对土壤结构具有一定的破坏性；后者精度和分辨率较差，不能对污染区域进行定量分析。常用的重金属污染检测物探方法有探地雷达法[8]、电磁法[9]、电阻率法[10]和激电法[11]。探地雷达法不适用于黏土、盐水和粉砂质地质，若地下有钢筋等结构，还会引起多次强烈反射，造成图像混乱不易分辨。电磁法测量需要发射幅值较大的电流，电磁噪声也会造成测量数据失真，减弱了深部探测的效果。直流电阻率法虽对污染区域具有较好的敏感性，但由于土壤自身的多孔结构，含水率和孔隙率以及污染浓度的不同都会对电阻率产生干扰，单一的电阻率特征量难以辨别污染区域的范围和污染程度。双频激电法是何继善院士提出的一种频率域激电法[12]，其仪器装备轻便、快速、精度高且抗干扰能力强。双频激电法观测参数为视幅频率和视电阻率，通过多参数观测可以准确反映目标体的范围和性状。刘志民[13-15]等基于双频激电法原理，在地下全空间三维层面上提出一种聚焦双频激电法超前探测技术，并开展了煤矿含导水有害地质构造探测的理论与实验研究。随着双频激电法理论的发展，国内部分学者将其拓展到重金属污染场检测领域。张杰[16]研究了不同电极装置和Cole-Cole 模型系数对重金属污染场激电异常的影响。铬污染场在土壤中的迁移扩散会进一步加剧周围土壤的严重污染，因此，对铬污染场迁移所造成污染的范围和程度进行监测显得尤为重要。

铬污染监测需要解决的技术问题主要有如下几点：铬污染场的迁移过程会受到含水率、孔隙率、土壤的渗透系数以及弥散率等多方面因素的影响；其次，仅分析在平整地面下污染场的迁移不能够对实际工况中起伏地面所导致的激电数据波动作出准确解释；最后，由于实验模拟铬污染场迁移较为困难，如实际操作中无法控制铬溶液在土壤中的渗透，铬污染通常为不规则区域，铬污染区域的扩散受多种不确定因素的影响。因此，笔者先建立了铬污染场迁移模型，并验证了采用COMSOL 对污染体进行监测的精确度和可靠性，随后在污染场迁移模型的基础上采用中梯剖面和对称四极测深装置，开展基于双频激电对不同地形下污染场迁移激电参量变化规律研究，以期确定铬污染场迁移所造成的重污染区域方位，为铬污染场实时监测提供理论依据和技术指导。

1 污染场迁移模型及数值正演模拟

1.1 污染场对流−弥散模型

铬污染源迁移过程主要受对流和弥散作用的影响，其迁移过程变化规律满足如下方程：

式中：i和j为承压含水层矩形网格差分模型中单元节点的离散网格编号；t为迁移时间，s；θv为土壤的体积含水率；Dij为弥散系数张量；C为六价铬在地下水中的浓度，mol/m3；xi和xj为笛卡尔坐标；qi为xi方向的达西流速，m/s；n为反应次数；Rk为第k个反应的溶解污染物产率。

1.2 污染场迁移数值模拟

依据地下水流动基本规律和污染物迁移机理，基于有限单元法，利用COMSOL5.6 软件将达西定律模块和多孔介质稀物质传递模块进行全局的流动耦合，并构建了250 m×10 m 二维铬重金属污染场模型(图1)，材料1 为透水性差的粉质黏土，材料2 为透水性较好的细砂，材料3 为透水性良好的中砂。仿真中仅对材料的孔隙率、密度、质量含水率、渗透系数等参数进行单独设置，详细的模型参数设置见表1。在地表的凸起的部分是静储量的铬污染源，污染物为相对浓度3 mol/m3的铬离子溶液，其方位处于地表的50～100 m；上边界(y=0 m)设置降雨量为500 mm；压力水头设置在x=250 m，距地面5.4 m 处；地下水分界线设置在x=0 处，分界线两侧无流体通过；含水层底部(y=−10 m)设置无流动，即不透水；其余参数设置见表1。为提高求解精度和计算效率，采用四边形网格自适应算法对所建模型区域进行网格划分，在污染体区域和电极布置线附近使网格自动加密，在非数据采集区域令网格自动变疏[17]。边界条件和参数的设置参考文献[16]和文献[18]的数值正演模拟。

表1 模型参数Table 1 Parameters of the 2D model of chromium-contaminated sites

图1 污染场初始模型(未迁移)Fig.1 Initial model of a chromium-contaminated site(pre migration)

相关研究[19-20]表明，土壤中的孔隙率ϕ、质量含水率 θw以 及铬离子浓度λ(mg/kg)是影响土壤电阻率的主要因素，三者和土壤电阻率的关系可用阿尔奇公式[21]描述：

式中：ρ为土壤介质密度，g/cm3；λ为铬污染物浓度，mg/kg。

据式(3)可知，在密度一定的土壤中，依据污染场的污染物浓度、孔隙率及质量含水率，可计算出污染场的电阻率。

运用COMSOL5.6 软件模拟了污染场随时间变化的迁移过程，分别得到迁移时间为第10、第100、第200、第300、第400、第500 天的电阻率变化，如图2所示。

图2 不同时间污染场电阻率剖面图Fig.2 Resistivity profiles of a chromium-contaminated site at different times

由图2 可知，铬污染物10～100 d 内在粉质黏土区域的迁移中主要受重力影响，污染物视电阻率呈均匀阶梯状分布，由于粉质黏土的透水性很差，对流弥散作用不明显，污染区域未发生明显横向迁移。第100 天时地面污染物已彻底消失，污染深度达到4.7 m，此时受污染面积约为265 m2。第100 天起污染物进入细砂层后开始明显地沿横向进行迁移扩散，100～200 d 内污染区域的范围变化极大，污染物中心在横向上由50～100 m 迁移至122～127 m，且污染场已扩散至含水层内部，底部边缘来到了9.8 m，说明细砂的高渗透系数及含水层对污染场的迁移影响显著。从第200 天开始，铬污染物以污染中心(深蓝色区域)为辐射源，保持整个污染场向下向右扩散的同时向四周呈阶梯层状扩散，此时污染场已辐射出一块新的半椭圆状污染区域，其顶部在纵向上再次逼近地面，高度甚至超过了左侧污染区域的顶部。在第300 天时重污染区域已经完全离开细砂区域，此时整个污染区域介于细砂和中砂区域之间，有着向中砂区域继续渗透的趋势；此时受污染面积已经达到了746 m2，是第10 天的12 倍。迁移第400 天时，此时污染场右上部分已在横向上迁入中砂区域并大面积地在中砂区域内横向扩散，其余部分在含水层内向下继续迁移。第500 天时，中砂区及其附近已经囊括了将近一半的污染区域，说明高渗透系数的透水层对污染物有很好的吸附作用；此时污染场已经迁出模型范围向更深、更广的区域扩散，因此，尽早控制污染源的迁移是十分必要的。由图2 可知，整体的污染区域随时间流逝逐渐增大，但深蓝色的重污染区域面积在逐渐减小，这是由于铬污染溶质不断向四周扩散，导致污染中心浓度略有下降。上述表明，地下有高渗透系数的透水层或富水土层可加速污染扩散，导致重金属污染区域面积快速增大，甚至会产生多个重污染主体区域。

2 数值正演模拟与土槽模型实验对比分析

考虑到无法控制铬溶液在土壤中的渗透且铬污染区域不规则等实际因素，搭建铬污染物运移过程的土槽物理实验模型十分困难，故文中采用COMSOL5.6软件对铬污染场迁移过程的电法监测进行数值正演模拟。本节通过静态土槽物理模型实验来验证数值正演模拟的可靠性和准确性。

2.1 实验方案设计

选定实验区域(6 m×2 m)，经检测区域内地表土壤平均电阻率为537 Ω·m，铬污染体的规格为50 cm×40 cm×20 cm，如图3 所示。底层15～20 cm 处为干燥黏土，其电阻率约为759 Ω·m，作用是为了保证铬溶液储存在细砂中不会向下渗透流失。中层5～15 cm 处为铬污染区域，采用具有较高吸水性和渗透率的细河砂，粒径为0.25～0.35 mm，将细河砂研磨(图4)并过土壤筛后将其压实。细砂经装填、压实完毕后，在表面均匀置入2 mol/m3的Na2CrO4溶液(图4 烧杯内黄色液体)，静置1 h 使铬溶液渗透并与细沙充分混合。污染体顶部土壤为就地取材的砂土，将这类砂土置于顶部0～5 cm 处。将铬污染体制备完成后，经测定此时铬污染体深度5～15 cm 处平均电阻率约93 Ω·m。

图3 铬污染体构造Fig.3 Structure of chromium contamination body

图4 细砂颗粒大小的处理Fig.4 Processing of fine sands

搭建土槽物理实验模型如图5 所示。铬污染体置于区域中央，埋深为5～25 cm 处。采用中间梯度布极方式，设A、B为供电电极，极距布置为6 m，M、N为测量电极，极距为10 cm，采用YDZ75(A)型并行直流电法仪进行探测，由发射模块发射100 mA 电流为激励，通过接收模块进行数据采集与处理。

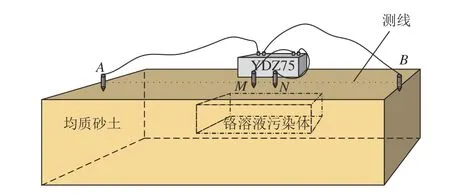
图5 土槽物理实验模型Fig.5 Physical experimental model of a soil bin

2.2 双频激电法中Cole-Cole 模型

在使用双频激电法进行污染场探测时，其激发极化效应参量视幅频率Fs由两测点间的电位差ΔVMN进行计算，其表达式为：

式中：ΔVH和 ΔVL分别为高低频电流供电时，测量电极MN间所测得的高低频电位差，mV。

另一激发极化效应参量视电阻率ρs按下式计算：

式中：j为电极装置系数，m；ΔVMN为高频电流供电时，测量电极两测点间的电位差，mV；I为高频供电电流，A；AM、AN、BM、BN为4 个电极间距，m。

复电阻率模型在地质勘探中已有广泛的应用[23],刘豪瑞等[24]通过铬污染土壤实验，验证了复电阻率Cole-Cole 模型表征土壤复电阻率的可行性。Cole-Cole 模型作为研究人员常用的描述激电效应的模型之一，其频谱参数与岩石、土壤物性参数以及测量数据等有关，可以有效地评价激电异常情况。本研究在数值正演模拟中引入Cole-Cole 复电阻率模型，该模型充分考虑了污染物浓度、土壤颗粒均匀程度、孔隙度及污染物致密程度等因素对污染场激电效应的影响。Cole-Cole 在频域内可表示为：

式中：ω为角频率；ρz为零频电阻率，相当于时间域下的直流电阻率；α为极化率；τ为时间常数；c为频率相关系数，0.1≤c≤0.6。其中ρ0表征导电性；α表征激电效应强弱；τ为激电谱变化频段位置参数；i 为虚数单位；c表征了目标体在激电谱中的异常段相对于背景场正常段的显现程度。

需对污染场的材料电导率和相对介电常数进行设置。其中电导率 σ等于Cole-Cole 模型零频电阻率的倒数，相对介电常数 εr与Cole-Cole 模型中的极化率α有关，二者在数值模拟中设置如下：

式中：下标序号代表的是对不同地质体和污染体区域的编号，见表2。

表2 模型参数的设置Table 2 Parameters of the Cole-Cole model

采用双频激电法，以中梯剖面装置对铬污染体进行数值模拟监测，在仿真开始之前需对发射电流及其频率进行设置：以超低频正弦波电流为激励，选定双频电流的频比S=fH/fL=13，高频(fH)为4 Hz，低频(fL)为0.308 Hz，电流幅值为0.1 A。

表2 中详细介绍了仿真中预先设置好的模型参数，其中dom_C 为点电流源的设置，代表了供电电极和测量电极位置。此处将各区域时间常数τ和频率相关系数c设置为同一值，这可最大限度忽略由地质影响、污染深度等方面带来的影响；仅对α值设置了不同的值，保证了铬污染区域在激电谱中异常段的明显呈现。

COMSOL5.6 中仿真模型如图6 所示。污染体置于整个围岩区域中心，沿x、y、z三个方向的尺寸分别为50、40、20 cm，其顶部距地面5 cm。模型中背景电阻率值设定为537 Ω·m，铬污染体0～ 5 cm 层设定电阻率值也为537 Ω·m，中间层5～15 cm 设定电阻率值为93 Ω·m，底层15～20 cm 设定电阻率值为759 Ω·m。

2.3 实验结果分析

数值正演模拟中，基于双频激电法引入Cole-Cole 模型后算得电位值，结合式(4)、式(5)分别计算视幅频率和视电阻率，与实验所测数值共同作出视电阻率和视幅频率特性曲线如图7 所示。可以发现图中视幅频率Fs曲线形态与倒置的视电阻率ρs曲线相似，且在同一测点上有良好对应关系。

图7 实验与仿真模拟结果对比Fig.7 Comparison between experimental and simulated values

为进一步分析COMSOL5.6 仿真的精确性，需进行误差分析(表3)，因实验与仿真中污染场均为对称结构，因此取点号1−点号30 进行误差分析即可，相对误差δ可表示为：

表3 实验与仿真误差分析Table 3 Experimental and simulation errors

式中：x为仿真值；a为实验值。

由图7 及表3 可知，在监测区域边缘处(点号1−点号20)，由于实验中此处土壤未经处理，土壤颗粒性状的差异会对视电阻率值造成扰动，FS和ρs的相对误差皆不大于3%，说明COMSOL5.6 对无污染区域也具有相当高精度的探测效果。在点号21−点号27 内，实验值与仿真值的FS和ρs的相对误差都超过15%，这是由于仿真中污染体只固定在所设方位，并不会向周围进行渗透；而实验中细砂内部铬溶液并未完全干燥和挥发，仍会渗透进入周围土壤之中。当M、N测点逐渐接近铬污染体时，视电阻率ρs逐渐下降，且在铬污染体投影位置处(点号28−点号30)，实验值与仿真值的FS和ρs的相对误差皆小于5%。综上，利用基于双频激电法引入Cole-Cole 模型对铬污染场进行监测是可行的。

3 铬污染场迁移双频激电法监测数值正演模拟

3.1 不同地形条件数值模拟

双频激电法中最常用的剖面探测装置为中梯剖面装置，其布极灵活且可以减少移动供电电极的次数，旁线测量所获得的数据可以充分对目标异常体的信息进行解释。对称四极测深装置所需的供电电流小，但却能获得较大的电位差，且在复杂地形工况条件下更有优势，也常作为双频激电法探测的主要装置。鉴于二者的优点，本文采用中梯剖面和对称四极测深装置对污染场迁移探测进行数值正演模拟。发射电流的高低频率仍设置为高频4 Hz，低频0.308 Hz，电流取0.25 A。

数值正演模拟中以1.2 节中10～400 d 的污染场迁移模型为基础(第500 天时污染场分布与第400 天相近，第500 天时已迁移出模型外，因此不予考虑)。由于铬污染场多为地形起伏的复杂地质工况，需考虑平整和起伏地形两种地质工况；分别采用中梯剖面装置和对称四极装置进行数值正演模拟。

3.1.1 中梯剖面数值正演模拟

以第100 天污染场迁移模型为例，构建不同地形污染场中梯剖面探测模型如图8 所示，图8b 中每个山谷凸起高度为2 m，宽度为50 m；其他天数下的污染场迁移探测模型中，电极排布方式与图8 相同。为得到更精确的激电异常数据，将AB电极设置在测线两端，测量电极MN极距设置为5 m，图8a 和图8b 中每个点号间距均为5 m(地形起伏时每个测点水平距离为5 m)，测点共计50 个。分别得到10～400 d 污染场不同地形时的视幅频率和视电阻率变化规律如图9 和图10 所示。

图8 不同地形污染场中梯剖面探测模型(第100 天)Fig.8 Intermediate gradient detection models of chromium-contaminated sites with different terrains (day 100)

图9 不同天数下污染场视幅频率变化曲线Fig.9 Variation curves in the apparent amplitude frequency of chromium-contaminated sites on different days

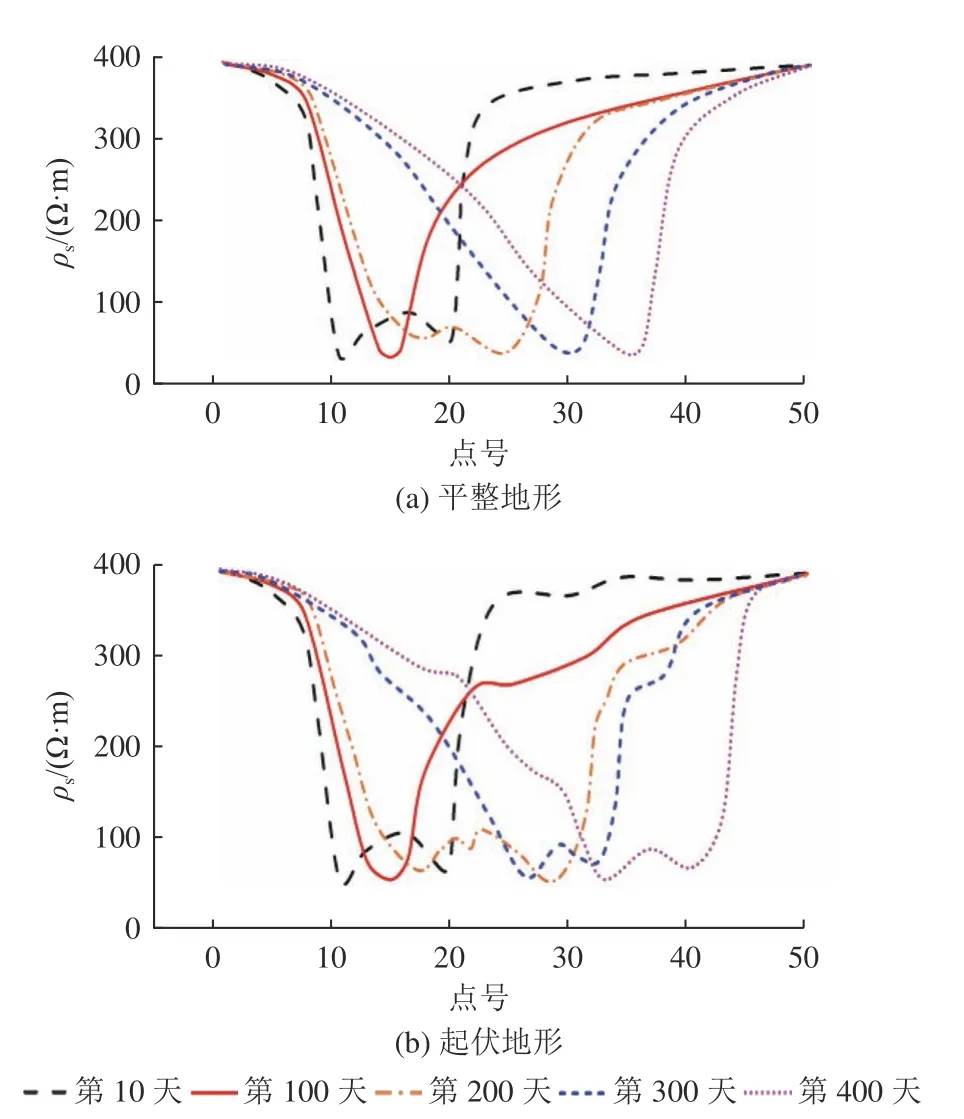
图10 不同天数下污染场视电阻率变化曲线Fig.10 Variation curves in the apparent resistivity of chromiumcontaminated sites on different days

由图9a 可知，在平整地形时，污染场迁移第10 天时的视幅频率值由点号8 的1.5% 跳跃至点号11 的13.6%，这是由于第10 天时地面有大浓度的铬污染物留存，使得地面污染区域和渗入地下部分同时产生激电异常，造成视幅频率在污染源边界上出现跳跃。第100、第200、第300 和第400 天时重污染区域中心深度分别为2.2、3.9、5.2、5.5 m，相应的视幅频率峰值分别为10.27%、8.50%、7.58% 和6.30%，表明当污染场向下扩散时，视幅频率的峰值随着时间增加而逐渐下降，这是由于随着污染场迁移深度的增加，能够被检测到的二次电位值逐渐降低，激电效应异常已变得不明显。第100、第200、第300 和第400 天时重污染区域中心在地面投影方位分别为75、130、153、178 m；相应的视幅频率峰值所在测点号分别为15、25、30 和35，表明当污染场向右迁移时，视幅频率峰值的测点号数值也逐渐增大。随着时间的增加，视幅频率曲线的夹角也逐渐增大，表明所检测土壤区域受污染范围在增大。在第200 天时，由于细砂透水性良好，在对流弥散作用下使污染区在横向上扩散明显，迁出细砂区域的部分又受含水层及压力水头作用在纵向上有明显扩散，导致此时在点号15−点号25 处视幅频率出现了双峰值，左侧峰值代表的是细砂区域中存留的污染较重部分(图2 中深蓝色所对应的低阻部分)，右侧峰值代表重污染区域部分(图2c 中的黑蓝色半椭圆部分)。

由图9b 可知，在地形起伏时，视幅频率曲线变化规律总体趋势与平整地形时相类似，但曲线的光滑程度要比平整地形时差，因此，对污染主体的判断会受地面起伏的影响。从图中还可以看出，第10 天和第100天时污染场距离地面较近，污染区域顶部的山峰正好覆盖在其正上方，且此时污染场呈纵向迁移趋势，未进行明显地横向扩散；此时对于一个重污染区域，视幅频率曲线与平整地形相比无明显变化，说明凸起的山峰对视幅频率曲线形态影响不明显，仅削弱了视幅频率的监测数值。第200、第300 和第400 天时，在山谷位置(点号20、点号30 和点号40)都引起了视幅频率曲线的明显波动，导致视幅频率曲线出现了“多峰”效应，说明监测时避开山谷位置可以更好地由曲线形态分析重污染区域数量和方位。

由图10a 可知，第100、第200、第300 和第400天时视电阻率曲线谷值对应的点号分别为15、25、30和36，与图9a 相对照，图10a 视电阻率曲线的谷值对应着视幅频率曲线的峰值，这与重污染区域的方位几乎一致。而图10b 中视电阻率曲线受地面起伏的影响，在山谷位置处也会造成一个重污染区域产生“多谷”现象，可见仅根据视电阻率图无法精确判断重污染区域方位。2 种地形下出现谷值的测点号随着污染源向右迁移而增大；所有视电阻率曲线的谷值都在30～60 Ω·m 附近，表明污染源向下迁移对视电阻率曲线的谷值无明显影响。

3.1.2 对称四极测深数值正演模拟

以第100 天污染场迁移模型为例，构建不同地形污染场对称四极测深探测模型如图11 所示，其他天数下的污染场迁移探测模型中，A、B电极的排布方式3个测点方位与图11 相同。为使有足够区域向左布置A电极，此处在污染场左侧增大了模型范围，模型宽度由250 m 向左增加至300 m。为了使得模型在足够深的位置仍可反映激电水平，将模型底部设置为接地。在2 种地形上分别设有601 个点位，每个点位水平间距0.5 m，测量电极M、N水平间距为1 m，O为MN中点；在2 种地形上用某一测点进行测深工作时，A、B电极向两端逐步增大，分别取75 组AB位置，即分别测量75 组电位值，则AB水平间距由2 m 逐步增大至76 m。仿真探测中分别在平整地形和起伏地形工况条件下布置了3 个方位的测点：测点O1布置在污染场正中心上方；测点O2布置在污染场左边缘中心；测点O3布置在污染场投影范围之外。

图12 的视幅频率和图13 的视电阻率曲线图皆采用对数坐标，以AB电极水平净距的1/2 为横轴，此方式能较好地反映污染场埋于中、深部的异常情况；且采取AB/2 为横轴时，在0～100 m 测深段内，测量深度与实际深度趋于一致[25-26]。

图12 不同天数下污染场测深视幅频率变化规律Fig.12 Laws of changes in the apparent amplitude frequency of chromium-contaminated sites on different days obtained using symmetrical quadrupole sounding

图13 不同天数下污染场测深视电阻率(测点O2)Fig.13 Apparent resistivity curves of chromium-contaminated sites on different days (measurement point O2)

平整地形时测深所得视幅频率曲线如图12 所示。由图12a 可知，污染场迁移第10 天时，测点O1−测点O3所测延线的视幅频率峰值分别为7.82%、4.88%、1.97%，表明在污染场中心正上方布置测点能够探测到较大的激电异常，越往边缘布置测点激电异常越不明显。污染场迁移第10 天时污染场埋深很浅，其所有测点下的曲线皆呈二层形态，视幅频率Fs随极距AB增大而减小，据曲线信息可估计出污染场底部埋深。当污染场继续向下迁移至离开地表时(100～400 d 时)，测点O1所得的视幅频率曲线仍呈二层形态，Fs变为随极距AB的增大而增大，据曲线信息可估计出污染场顶部埋深。在100～400 d 内，无论污染场距离地面远近，测点O2和测点O3所探测到的视幅频率曲线皆呈三层形态。以第100 天时为例，此时测点O2的视幅频率激电异常幅值约为测点O1下的90%，测点O3约为测点O1的34%；虽然二者所测视幅频率幅值比测点O1低了许多，但由测点O2和测点O3的视幅频率曲线凸起部分所对应的横轴坐标可更好地估计出污染场的顶、底部埋深。测点O2较测点O3的优势在于，当污染浓度最大的部分迁移深度增大时，由测点O2所得到的视幅频率曲线的异常衬度(异常衬度指异常相对背景值的明显程度，定义为异常最大值和正常场值之比)更大，即激电效应越明显。

起伏地形时测深所得视幅频率曲线如图12b 所示，视幅频率Fs曲线形态变化总体趋势仍与平整地形相类似，但受到地形起伏影响会略有小幅波动。测点O1所探测到的视幅频率Fs激电异常随着天数增大而减小，但曲线皆呈二层形态，无法判断污染场底部埋深情况。测点O2所测曲线可较为准确地估计出污染场顶部和底部埋深，其异常衬度也较测点O3更大。

通过上述分析，在2 种地形中测点O2都是三个测点中测深效果最佳的，现作出测点O2所对应的视电阻率变化曲线(图13) 以进一步分析。由图13 可知：对称四极测深下，地形起伏会造成视电阻率值的波动，但不会影响视电阻率的谷值，即污染源中心的视电阻率为定值(约为45 Ω·m)，这与3.1.1 节中梯剖面测量所得结果一致；且污染源向下迁移对视电阻率曲线的谷值无明显影响。以剖面时的图9、图10 为一组，测深时的图12 中的测点O2、图13 为另一组，2 组相比可得，测深中视幅频率峰值与视电阻率谷值在同一深度上的对应关系较剖面中同一投影方位的对应关系要差。

3.2 污染场重污染区域方位的确定

综上可知：综合污染场的视幅频率和视电阻率曲线可有效地确定污染场重污染区域的具体方位；在对称四极测深时，采用在污染场边缘布置测点可更好地对污染场顶、底部埋深作出判断。本节以第100 天时污染场迁移模型为例，综合污染场视幅频率和视电阻率监测曲线，作出综合剖面图和测深图(图14)，2 种地形的测深图中均对测点O2进行监测。

图14 污染场视电阻率和视幅频率综合图(第100 天)Fig.14 Composite curves of apparent resistivity and apparent amplitude frequency of chromium-contaminated sites (day 100)

污染物迁移第100 天时，受污染区域在地面投影的确切位置为50～100 m 处，在平整地形下的深度为0.1～4.7 m 处，其中污染较重的区域顶部深度在1.5 m处，此时重污染区域的埋深范围为1.5～4.7 m；在起伏地形下受污染区域深度为2.1～6.7 m 处(山峰高为2 m)，污染较重的区域顶部深度在3.5 m 处，此时重污染区域的埋深范围为3.5～6.7 m。由图14 可知，在平整地形下，铬重污染区域水平投影方位位于54.2～91.8 m，与模型相比相对误差为4.2～8.2 m，与确切方位重合度达75.2%；测深方位位于1.9～4.3 m，相对误差为0.4 m，与确切方位重合度达75.0%。在起伏地形下，水平投影方位位于50.2～95.8 m，与模型相比相对误差为0.2～4.2 m，与确切方位重合度达91.2%；测深方位位于3.15～8.4 m，相对误差为0.35～1.7 m，顶、底部的监测数值皆已超出确切方位边缘。

综上可知，在污染场边缘布置测点，以污染场的视幅频率和视电阻率曲线综合判定重污染区域时，在两侧的山陲上布置供电电极可更精确地确定污染场方位，这是由于供电电极导入大地的电场线会受山陲影响而产生一定的聚拢效果，从而更好地去诱导受污染区域产生极化现象。

4 结论

a.建立了标志性富水土层地质模型，分析得到重金属铬污染源迁移过程会受高渗透系数透水层吸附，从而在横向上加速污染的扩散；在渗透层边界，污染区域有再次向地面逼近的趋势。

b.中梯剖面探测中，平整地形探测时，视幅频率曲线峰值与视电阻率谷值具有良好的对应关系；起伏地形探测时，山谷的出现会使得一个重污染区域的视幅频率曲线呈现“多峰”现象，而山峰对视幅频率曲线无明显影响。

c.对称四极测深中，当测深测点距离污染体达到污染体投影在地面长度的一半时，对较深的污染区域而言，视幅频率幅值异常不明显；将测深测点布置在污染场投影的边缘中心处时，视幅频率幅值异常明显且可有效反映污染区位置。与中梯剖面探测相一致，污染场迁移深度的增加会造成视幅频率峰值明显下降，而对视电阻率谷值无明显影响。

d.在平整地形和起伏地形下，进行中梯剖面和对称四极测深探测时，可由视幅频率和视电阻率曲线交点来确定铬污染场重污染区域的方位；当在凸起山峰两侧的山陲上布置供电电极，可更精确地确定污染场区域方位。