180 m跨景观钢桁架桥风致振动试验研究

陆 军，张杭斌，黄 青，刘陆海，郑建荣

1.浙江省轻工业品质量检验研究院,浙江杭州 310018

2.比木（浙江）工程咨询有限公司，浙江杭州 310005

3.杭州滨江水务市政工程有限公司,浙江杭州 310051

4.杭州滨江环境发展有限公司,浙江杭州 310051

0 引言

按现行的《公路桥涵设计通用规范（JTG D60—2015）》［1］规定：跨径大于100 m的钢梁桥的驰振稳定性应在模拟结构阻尼比的条件下通过气动弹性模型试验进行检验。从安全的角度出发，笔者单位首先请教了西南交通大学桥梁系的有关专家，得出结论如下：理论上讲，本桥一阶跨中竖向频率为0.71 Hz 左右，存在风致涡振的可能，但由于本桥是钢桁架结构，杆件多，桥面中间上下透风，桥面窄，因而有效地阻止了卡门涡街的形成，涡振发生的可能性较低；且桥轴向与钱塘江主航道平行，横桥向大风工况本身出现的概率也不大。然后，笔者单位还根据设计要求委托同济大学作了风洞试验，得出的结果与西南交通大学专家的观点非常一致。

1 工程概况

杭州市滨江区沿钱塘江区域景观提升项目——绸桥（图1），位于滨江区闻涛路以北，钱塘江南侧沿岸，萧山排灌船闸位置，与萧山排涝站站房平行，上跨排涝和通航航孔及江堤防汛通道（图2）。绸桥结构为简支拱形张弦钢桁架组合体系，桥梁跨度180 m，桁架截面为三角形，截面高度3.5～8 m不等（中间大两头小），截面宽度6～12 m 不等（中间小两头大），左右下弦杆外侧各向外水平悬挑4 m宽的桥面，桥总宽度14～20 m不等，桁架拱高7 m（图3）。钢桁架桥梁上弦杆为2-Φ900×45 mm哑铃型双管组合截面，下弦杆为Φ700×30～Φ900×45 mm 钢管，竖杆、斜腹杆为Φ350×16～Φ500×30 mm 钢管，端支杆为□1 200×1 200×50，总用钢量约1 800 t，钢板材料选用Q390GJB 钢。拉索采用（Galfan）6Φ140密封索，强度1 470 MPa，有效面积13 900 mm2，单根拉索最大拉力设计值6 400 kN，静载破断荷载18 700 kN。支座形式为抗震球形铰支座：东侧支座采用固定支座GD和单向支座DX，西侧支座采用单向滚动支座DX和双向支座SX（图4）。桥面设计均布活荷载为3.0 kN/m2，设计基本风速为29.4 m/s，支座竖向反力为9 125～9 180 kN，东侧GD 支座水平不平衡力矩为107 760 kN·m。承台结构设计采用5×6根Φ1 500长度为43.5 m钢筋混凝土钻孔灌注桩，承台外轮廓尺寸为27 m×22.5 m×3.0 m，由于地处钱塘江边，承台宽度受到江堤的限制，为抵抗横向风荷载引起的超大不平衡力矩，将东侧基础承台下沉3 m。

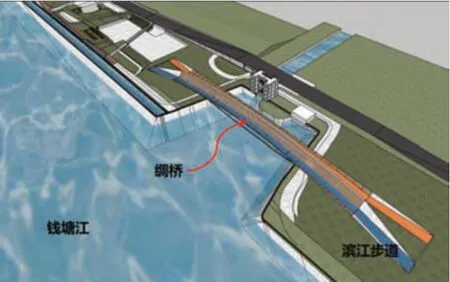
图1

图2 绸桥建成实景

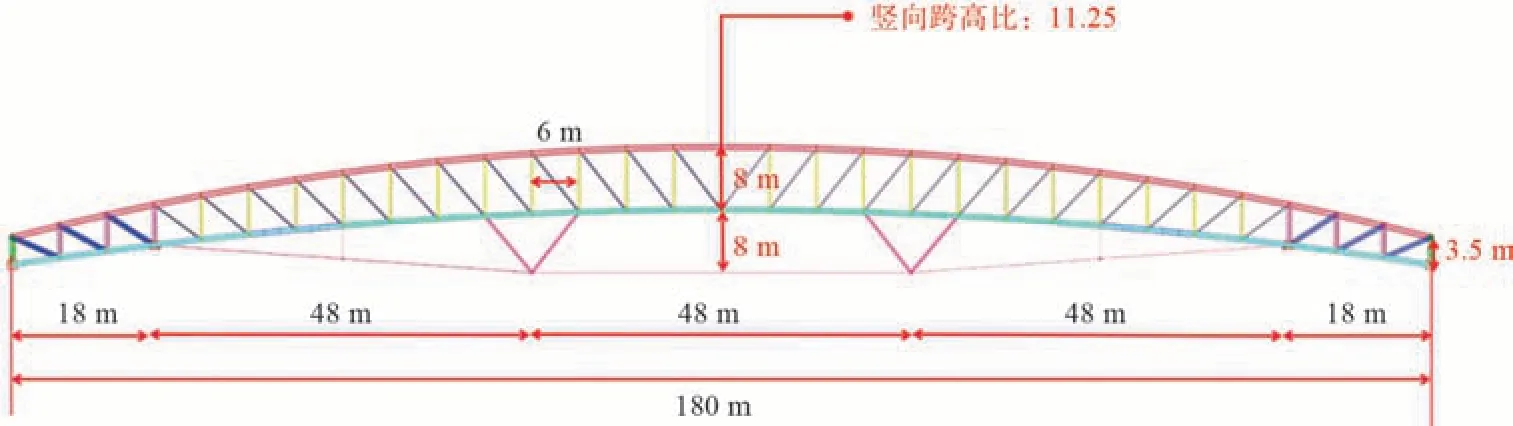
图3 绸桥桥型立面布置

图4 绸桥桥型平面布置（含支座）

2 风洞试验研究依据和目的

2.1 桥梁风致振动的概念

大跨度桥梁抗风稳定性根据失稳模式可分为静力失稳和动力失稳。静力失稳主要检验大跨度桥梁在静风作用下的稳定性，常见的失稳形式为主梁在升力矩作用下的扭转失稳形态。动力失稳主要是指桥梁的颤振、驰振，以及涡振问题。结构通过振动从空气中吸收能量，当结构从空气中吸收的能量大于结构本身的阻尼所耗散的能量时，桥梁结构就会产生发散性的自激振动，这就是桥梁的颤振或驰振；而当气流流经结构断面（包括主梁和桥塔结构）时，由于漩涡的交替脱落频率与桥梁结构的自振频率接近时，会产生桥梁的振动锁定现象——涡激振动，此时虽然涡激力不大，但由于脱落频率和结构频率接近，因此结构也会出现很大的振幅，并严重影响结构的使用性能［2］。

除此之外，由于自然风包含大量的脉动成分，因此需要对结构在脉动风作用下的响应作进一步的研究，来保证结构的抗风安全，即抖振响应。考虑在工程上应用的便利性，我们通常将随机变化的自然风分为平均风（不随时间变化）和脉动风（又称为紊流）两部分。一般意义上，平均风作用下主要产生结构的自激振动（颤振或驰振）和涡激振动；而紊流风作用下，结构振动对应的是一种脉动风（紊流风）作用下的随机强迫振动。

2.2 研究的依据

据现行《公路桥涵设计通用规范（JTG D60—2015）》［1］和《公路桥梁抗风设计规范（JTG/T 3360-01—2018）》［3］（以下简称《规范》）：钢塔桥及跨径大于100 m的钢梁桥的驰振稳定性应在模拟结构阻尼比的条件下通过气动弹性模型试验进行检验；当钢梁桥主跨径L≥100 m时，应利用全桥气动弹性模型试验进行涡激共振检验。本工程属城市人行天桥，而根据《城市人行天桥与人行地道技术规范（GJJ 69—95）》［4］局部修订的相关规定，人行钢天桥设计应按照《公路钢结构桥梁设计规范（JTG D64—2015）》执行。

2.3 研究的目的

2.3.1 检验大结构的动力和静力抗风稳定性

基于全桥气弹模型风洞试验及数值分析，对大桥在极端风作用下的颤振稳定性、静风稳定性进行数值分析及试验验证，确保桥梁的结构安全。

2.3.2 非破坏性风致振动检验

基于全桥气弹模型风洞试验，检验结构在设计风速范围内，涡激振动及抖振振幅是否在规范容许范围，评价在设计风速范围内的涡激振动性能；给出各级风速下主桥结构的抖振位移、加速度并评价其风致舒适性能。如出现振动超限情况，采取相应的气动措施或结构措施，保证结构正常使用状态下的振动性能满足要求。

3 试验前的相关风速和结构动力特性计算

3.1 设计基准风速

依据《规范》要求，绸桥位于浙江省杭州市滨江区，100年重现期对应的设计基本风速为U10=29.4 m/s。桥位处地表类别按B类地表考虑，对应的地表粗糙系数α0为0.16，地表粗糙高度z0为0.05 m。按《规范》4.2.4条规定，桥梁设计基本风速Us10为：

桥面距设计平均高潮位Z=16.28 m。根据《规范》4.2.6 条规定，桥面设计基准风速Ud按式（2）确定：

桥梁长度为180 m，按《规范》5.2 条规定，等效静阵风系数Gv取1.294，桥面设计静阵风风速为：

按《规范》7.2.5 条规定，绸桥采用风洞试验方法检验结构的静风稳定性能，故结构静风稳定性分项系数γai取1.4，静力扭转发散检验风速为：

按《规范》7.5.8 条规定，绸桥采用风洞试验方法检验结构的颤振稳定性能，故颤振稳定分项系数γf取1.15，风速脉动空间影响系数γt取1.336，攻角效应分项系数γα取1，故对应的颤振检验风速为：

3.2 计算桥梁结构动力特性

分析计算桥梁结构的动力特性，是为后期进行桥梁结构在风载效应下的桥梁抖振响应分析和全桥气弹模型风洞试验准备的基础性工作。为此，对绸桥结构通过有限元分析其在成桥状态下结构的动力特性，为下一步进行全桥气弹模型设计提供基础模型。

3.2.1 有限元计算模型

结构动力特性分析采用离散结构的有限元方法，其总体坐标系以顺桥向为X轴，以横桥向为Z轴，以竖向为Y轴［5］。动力特性分析采用ANSYS 公司授权的结构分析软件对该模型进行结构动力特性分析［6］。其中主梁采用空间三维梁单元（beam188单元）模拟；桥面板采用shell181板单元模拟；拉索采用link10单元模拟；阻尼器采用combin37单元模拟。对应的约束条件与设计保持一致。

3.2.2 动力特性计算结果

通过动力特性分析，可以得到成桥状态的动力特性，见表1。成桥状态有限元模型见图5，前10 阶动力特性分析结果见表2（其中振型的第1～5阶、第10阶）。分析表明，该桥第一阶竖弯频率为0.714 0 Hz，该桥第一阶侧弯频率为0.371 3 Hz，该桥第一阶正对称扭转频率为1.071 1 Hz。

表1 成桥阶段前10阶振型及频率

表2 典型的成桥阶段振型

图5 成桥状态有限元模型

4 风洞试验模型的制作、调试及模型动力特性检验

4.1 气弹模型设计原则

除了满足结构气动外形及风场特性这些相似条件外，全桥气弹模型风洞试验还必须保证结构气动弹性特性满足一定的相似率（结构的长度、密度、弹性和内摩擦的相似条件以及气流的密度和黏性、速度和重力加速度等相似条件）［6］。

这些物理量可以用表3所示无量纲参数的相似性条件，来满足全桥气弹模型试验的要求。

表3 无量纲参数的相似要求[6]

本试验在TJ-3风洞进行，存在试验室边界层风洞尺寸15 m×2 m（宽度×高度）及模型阻塞比（5%以下）等硬性限制条件，本绸桥研究的模型选用1∶36尺寸比例。除Reynolds 数、Cauchy 数以外，其余4 个无量纲参数在该全桥气弹模型风洞试验中得到了严格模拟。全桥气弹模型的部分参数相似比关系见表4。

表4 全桥气弹模型部分参数的相似比

4.2 气弹模型设计

结构气弹模型设计以结构设计图和动力特性分析结果为主要依据。

依据刚度的相似比要求，设计符合竖弯、侧弯及扭转刚度要求的T形截面钢骨架，T形梁的中心线与实际拱形钢桁架形心线一致。截面芯梁见图6。

图6 结构芯梁和钢骨架设计（单位：mm）

4.3 外形尺寸模拟

依照外形尺寸相似比的要求，对结构的主要抗风构件进行拆解加工，其中包括总体桁架结构、桥面板单元、桥梁风障装置以及预应力拉索，外形保证与原结构一致，尺寸按照几何比例缩放。

4.4 质量系统模拟

为了能够准确反映桥梁结构在风荷载下的动力响应大小，除了通过几何外形及风场模拟保证风荷载的一致性，还需要通过弹性刚度即质量系统的严格相似保证结构的动力特性一致性，弹性刚度相似性在主梁芯梁设计阶段已得到满足。要保证结构的质量系统一致，需要在扣除芯梁和外表皮所提供的实际质量和质量惯矩，采用铅块砝码为配重补充不足部分的质量体系进行调整［2］，即该部分通过外表皮拼装完成后，通过调整质量配重块的位置保证振型和频率的一致性，最终确保质量系统的一致性。

4.5 模拟试验流场

全桥气弹模型风洞试验流场分为：均匀流场和紊流场［5］。均匀流场是指风洞中没有任何障碍物时的空风洞流场。通过采用风速仪和风压计对空风洞均匀流场进行测试，风场紊流度小于1%。全桥气弹模型桥面高度处的紊流强度Iu<1%；紊流场的模拟实际桥位处边界层风环境可以近似采用尖劈和粗糙元来模拟。

4.6 试验准备及布置

4.6.1 风洞试验主要仪器设备

TJ-3 边界层风洞：高2 m，宽15 m，长14 m；可调风速1～18 m/s；

管道公司南京处深化党员“师带徒”活动，以新入职员工为主，通过选师傅、订协议、明责任等方式，建立党员“传帮带”工作体系，完善党员“师带徒”成效评价和同奖同罚的考核机制，评选示范岗，促进青年人才快速成长。

TFI眼镜蛇三维脉动风速测量仪（Cobra Probe）TFI Series 100；

MEW-Matsuchita 光学位移计：MLS-LM10；

HP35670A信号分析仪：四通道FFT信号分析仪；

计算机采样系统：模拟式信号采样板，微机以及相应软件。

4.6.2 测量仪器布置

在气弹模型风洞试验中，主要测量风速和位移两个指标。流场测量的脉动风速仪主要布置在气弹模型中心处，探头可以自由调整离开风洞底面的高度。

风洞试验中的结构位移响应测量采用激光位移计，位移计分别在主梁四分点及跨中点各布置3 个位移计，同时可以测量竖向、侧向和扭转位移；全桥共布置9个激光位移计（图7），其中红色部分对应竖向位移计，蓝色部分对应侧向位移计，扭转位移通过计算两个激光位移计的竖向位移差反算得到。

4.6.3 检验模型动力特性

模型安装调试完成后，应检验结构动力特性，以确认气弹模型是否满足试验的要求。

本次风洞试验采用自由振动方法，分别测试了气弹模型第一阶侧弯、竖弯和扭转模态等的自振特性。基于动力特性测试的位移信号，分析了结构主要固有模态的阻尼比，以检验气弹模型的阻尼特性［8］。检验结论如下：风洞试验模拟的各种试验状态气弹模型的自振频率的模型实测值与期望值之间的相对误差均在±2%以内，模态阻尼比在0.8%以下，完全满足风洞试验的要求（表5）。

表5 成桥状态气弹模型动力特性检验[1]

5 全桥气弹模型风洞试验

5.1 气弹模型风洞试验工况

针对桥梁结构不同的施工阶段，模拟其在不同的风攻角和不同的流场下的响应，共进行了39个工况的全桥气弹模型风洞试验，各工况颤振临界风速见表6。

表6 成桥状态气弹模型风洞试验工况及颤振临界风速[2]

5.2 均匀流场各工况位移响应的比较

成桥阶段在均匀流场中比较了风攻角α为0°、+3°、-3°时在不同风偏角（0°、10°、20°、30°、50°）下的风洞试验结果，各工况结构颤振临界风速均大于60 m/s，大于颤振检验风速45.4 m/s，表明结构的颤振稳定性能有足够的保证。

从实验结果来看，在均匀流条件下，结构的动力响应较低，在不同攻角、偏角及风速下，均未发现明显的涡激振动现象及动静力失稳现象。以60 m/s的代表风速为例：结构跨中扭转位移角在10°风偏角，+3°风攻角时最大，为5.2×10-4°；结构跨中竖向位移在0°风偏角，-3°风攻角时最大，为-0.06 m；结构跨中侧向位移在0°风偏角，+3°风攻角时最大，为-0.392 m。对应的位移测点随风速、风偏角的变化见表7（列举以上三种最大位移）。在桥梁结构成桥状态39个工况的风洞试验中，均未观测到明显的竖弯涡振和扭转涡振现象。

表7 不同风攻角和风偏角的均匀场下结构位移相应极致值[1]

5.3 紊流场各工况位移响应的比较

成桥阶段在紊流场中比较了不同风偏角（0°～350°）下的风洞试验结果，各工况结构颤振临界风速均大于60 m/s，大于颤振检验风速45.4 m/s，表明结构的颤振稳定性能有足够的保证。对应结构跨中的扭转、竖向和侧向位移响应平均值及根方差见表8（列举以上三种最大位移）。

表8 0°风攻角和0°风偏角的均匀场下结构位移相应极致值[1]

从实验结果来看，在紊流场条件下，结构的动力响应高于均匀流场，在不同风偏角及风速下，均未发现明显的涡激振动现象及动静力失稳现象。以60 m/s 的代表风速为例：结构跨中扭转位移角在0°风偏角时最大，为2.7×10-3°；结构跨中竖向位移在0°风偏角时最大，为-0.024 77 m；结构跨中侧向位移在0°风偏角时最大，为-0.302 39 m。

对应的结构跨中的扭转、竖向及侧向位移随风偏角的变化见图8～10。

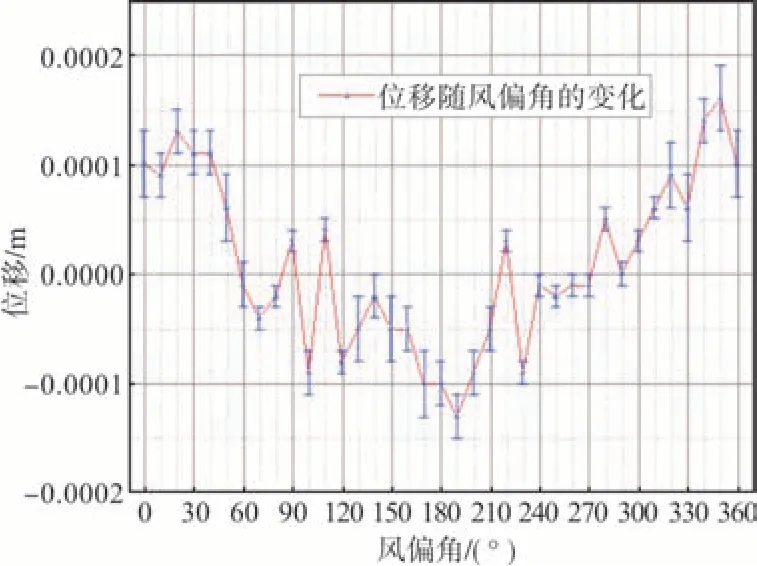
图8 紊流场跨中扭转位移随风偏角的变化曲线(代表风速36 m/s)

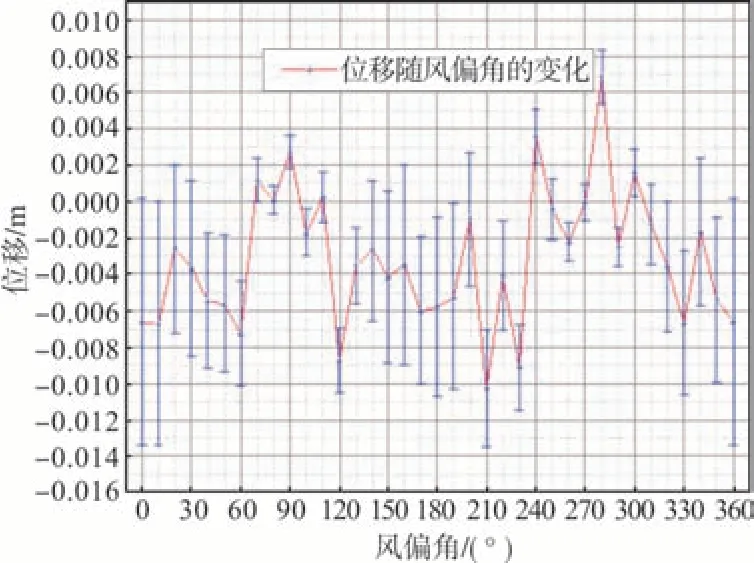
图9 紊流场跨中竖向位移随风偏角的变化曲线(代表风速36 m/s)

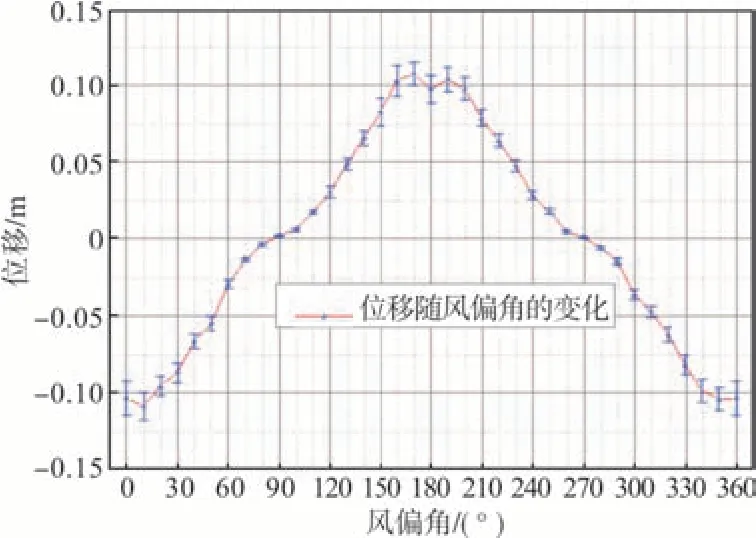
图10 紊流场跨中侧向位移随风偏角的变化曲线

6 结论

由以上的试验结果表明：

1）绸桥成桥状态下的颤振临界风速高于该桥的颤振检验风速（各工况结构颤振临界风速均大于60 m/s，大于颤振检验风速45.4 m/s），结构在成桥状态下的颤振稳定性满足设计要求。

2）在均匀流场或紊流场中，不同风偏角及风速下，均未发现明显的涡激振动现象及动静力失稳现象，表明结构的颤振稳定性能有足够的保证。

从试验结果分析，即使在60.0 m/s风速的风荷载作用下也不会发生静力失稳、颤振和涡激振动现象。

综上，本桥的抗风问题并不突出，虽然《公路桥梁抗风设计规范（JTG/T 3360-01—2018）》第8.2.3条有“当钢梁桥主跨径大于100 m时，应利用全桥气动弹性模型试验进行涡激共振检验”的要求，但对于人行桥，应视具体情况进行有差别的分析。