基于虚拟子阵列的多用户大规模MIMO混合预编码
张雷 高俊枫 向博
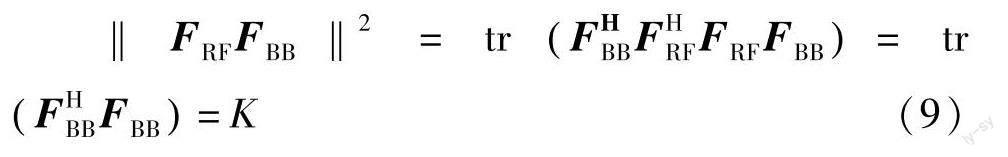

摘 要:为了在多用户大规模多入多出系统中获得更高空间分集增益,提出一种基于虚拟子阵列的部分连接结构模数混合预编码方案.此方案允许射频链路动态连接发射天线.首先通过提取空口信道的共轭相位设计模拟预编码矩阵,并提出逐元最大化虚拟子阵列增益算法以获得更大模拟预编码增益,然后对等效信道实施迫零数字预编码.仿真结果表明,Rayleigh衰落信道中所提虛拟子阵列方案比传统的部分连接结构方案能取得更高的频谱效率,且对相位量化误差不敏感.
关键词:混合预编码;大规模多入多出系统;部分连接结构;虚拟子阵列
中图分类号:TN929.5
文献标志码:A
0 引 言
在基站端部署大量天线的大规模多入多出(multiple-input multiple-output,MIMO)系统,通过对收发端简单线性处理,能极大提高系统频谱效率,因此成为第5代移动通信(5G)和后5G系统的核心技术之一[1-3].射频链路数远小于基站天线数的模数混合预编码可有效结合低维基带数字预编码和高维射频模拟预编码(后者通常用移相器实现),相较于全数字预编码可大幅降低成本和功耗,且性能损失较小,已成为大规模MIMO下行传输的主流方案之一[4].
混合预编码主要包含全连接和部分连接2种结构.全连接结构[5]的每个射频链路借助移相器连接至全体天线,移相器数多达射频链路数与天线数之积,成本和功耗较高.而部分连接结构[6-8]的各射频链路仅与不同天线子阵列连接,移相器数可减少至天线数.其中,文献[6]研究了基于最小估计误差的混合预编码框架,文献[7]设计了基于混合精度移相器量化的混合预编码方法,文献[8]则提出基于人工蜂群算法的混合预编码方案.然而,上述部分连接结构方案均局限于单用户场景,其数字预编码环节所用奇异值分解等难以用于多用户场景,损失了多用户复用增益,且所用算法常包含多轮迭代,复杂度高而难以实现.
为降低计算复杂度,文献[5]针对全连接结构多用户系统提出了相位迫零(phased zero-forcing,PZF)混合预编码方案,可分别求出模拟预编码和数字预编码的闭合解:前者通过提取下行空口信道矩阵共轭转置的相位而直接生成,后者则通过对等效信道矩阵采用迫零算法而得.此方案可获得与等增益发射相当的阵列增益,性能与全数字预编码较为接近.文献[5]的模拟预编码器设计思路最近已拓展至文献[9-12].文献[9]针对单用户场景,将该思路与奇异值分解的数字预编码结合.文献[10-12]则考虑多用户场景,将该思路与迫零数字预编码结合,分别提出了顺序子阵列、匹配子阵列和分布式子阵列方案,但仍未能充分探索大规模MIMO系统的空间分集增益,与全连接结构相比性能上有明显差距.
针对上述问题,本研究继承文献[5]及文献[10-12]利用空口信道的共轭相位设计移相值的基本思路,提出一种基于虚拟子阵列的部分连接结构多用户大规模MIMO混合预编码方案.此方案可动态调节射频链路与发射天线的连接关系,结合所提逐元最大化虚拟子阵列增益算法可获得更大的模拟预编码增益.基带仍对等效信道实施迫零数字预编码.分析和仿真结果表明,与已有部分连接结构方案相比,所提虚拟子阵列方案在稍微增大计算复杂度的前提下能大幅提高系统频谱效率,且对移相器的相位量化误差较为鲁棒.
本研究的相关符号如下:小大写斜黑体字母分别表示向量和矩阵;‖A‖和tr(A)分别表示A的Frobenius范数和迹;AH和AT分别表示A的共轭转置和转置;Cn×m表示n×m维复矩阵集;CN(λ,σ2)表示均值和方差分别为λ和σ2的复高斯随机变量;┌g┐表示向上取整;E(·)表示数学期望.
1 系统模型
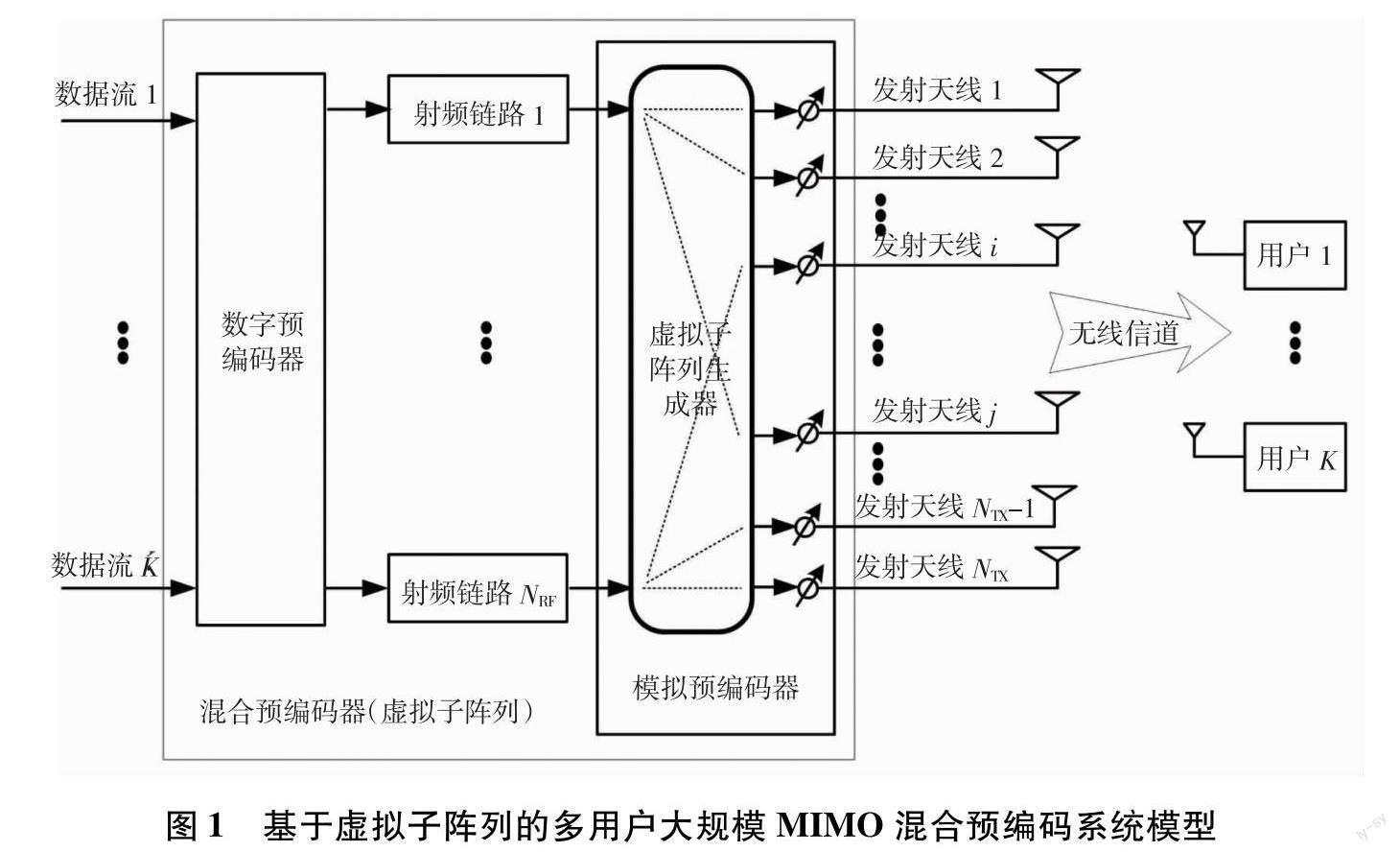
考虑图1所示多用户大规模MIMO下行链路.基站部署NTX个发射天线和NRF个射频链路,与K个单天线用户以空分形式通信并向每个用户发射单数据流,且满足K≤NRF≤NTX基本约束条件.虚拟子阵列生成器将全部发射天线划分为NRF个虚拟子阵列,且每个子阵列的天线数为M=NTX/NRF.第nn=1,2,…,NRF个射频链路仅通过移相器与第n个虚拟子阵列的M个天线相连.
设信道为平坦衰落,则用户k的接收信号rk为
rk=hTkFRFFBBs+nk(1)
式中,hk∈CNTX (k = 1,…,K)表示基站到用户k的信道向量;FRF∈CNTX ×NRF和FBB∈CNRF×K分别为模拟预编码和数字预编码矩阵,一般仅通过移相器调整FRF的相位,但可同时改变FBB的幅度和相位,此外须满足‖FRFFBB‖2=K的总发射功率约束;s∈CK表示基站向K个用户发射的信号向量,并且满足EssH=(P/K)IK,P为总发射功率;nk~CN(0,1)为用户端噪声.由此,用户k对应的信干噪比ρk可表示为,
式中,fBB,k为FBB的第k列.一般可用频谱效率R度量系统性能.
2 基于虚拟子阵列的混合预编码
2.1 基本思路
混合预编码的优化设计目标为
式(4)通常是联合非凸优化问题,难以获得最优解.为降低复杂度,拟对FRF和FBB解耦求解.考虑到适用于多用户分布式接收特点的迫零数字预编码技术已广泛应用[5,10-12],且为求出简单闭合解,本研究采用的基本处理框架与文献[5]及文献[10-12]相似,即“空口信道的共轭相位模拟预编码+等效信道的迫零数字预编码”.同时,为获取更大空间分集增益,提出允许发射天线动态连接射频链路的虚拟子阵列新方案.有研究阐明,在模拟域增加阵列增益可提高混合预编码系统频谱效率[10].因此,利用不同收发天线对的信道系数幅度波动较大的特性,提出可以最大化虚拟子阵列增益的模拟预编码矩阵求解算法,从而增加系统频谱效率.
2.2 虚拟子阵列的模拟预编码向量构造
虚拟子阵列生成器动态生成射频链路和发射天线之间的连接关系,而该连接关系和移相器的相位值均依赖于FRF的计算结果,而FRF又与下行信道信息直接相关.假设基站可获取下行信道矩阵H.H中元素hk,nTX(k=1,2,…,K,nTX=1,2,…,NTX)表示基站第nTX个天线到第k个用户的信道系数,并记hk,nTX的幅度和相位分别为|hk,nTX|和φk,m.
设所有发射天线和所有用户的序号集合分别为A={1,2,…,N}和U={1,2,K,K}.在部分连接结构中使用移相器实现模拟预编码的约束条件下,利用信道系数相位信息生成移相值,本质是通过某种准则,对第n个射频链路,在所有K×NTX个候选信道系数中选择合适的用户k的M个信道系数的相位,以构造虚拟子阵列n对应的模拟预编码向量fn,即
由此可认为通过该准则在射频链路n与发射天线子集{m1,m2,…,mM}之间建立了连接关系,即生成了由发射天线子集{m1,m2,…,mM}构成的与射频链路n对应的虚拟子阵列n,且不同射频链路的虚拟子阵列之间没有交集.此外,可根据fn每个元素的相位确定与发射天线子集{m1,m2,…,mM}對应移相器的移相值.
2.3 逐元最大化虚拟子阵列增益算法
在模拟预编码向量fn的作用下,虚拟子阵列n(对应射频链路n)获得的子阵列增益ηn为
式中,wk,{m1,m2,…,mM}表示由H中第k行第{m1,m2,…,mM}个元素{h(n)k,m1,h(n)k,m2,…,h(n)k,mM}构成的信道行向量,此处上角标n表示与第n个射频链对应.注意到ηn是关于k和{m1,m2,…,mM}的函数.显然,对每个虚拟子阵列n,获得使ηn最大化的k和{m1,m2,…,mM}值是最优解,即
但需要在K×NTX个候选信道系数中实施M维向量穷举搜索,复杂度很高,且搜索得到的不同虚拟子阵列n对应的{m1,m2,…,mM}值可能重叠,与部分连接结构要求相悖.
因此,本研究提出如下逐元最大化虚拟子阵列增益算法,以替代上述高复杂度的穷举搜索,其主要思路是:逐次对每发射天线在当前可选信道系数中选择幅度最大的,且考虑到用户公平性,保证每个用户对应信道系数被选中的次数相同,同时,建立了虚拟子阵列n(射频链路n)和发射天线子集{m1,m2,…,mM}及相应移相值之间的对应关系.该算法可获得较大的虚拟子阵列增益和模拟预编码增益,从而优化FRF的设计并提升系统频谱效率.
逐元最大化虚拟子阵列增益算法如下:
输入:H所有元素的幅度和相位,Q=「NRF/K┐.
输出:将所有生成的FRF(nTX,koptq,nTX)按对应行列序号构造得到模拟预编码矩阵FRF.
1)for q=1:Q
2)if q 4)elseif q=Q 若某用户对应的信道系数被选中达M次,则在后续查找中将该用户的信道系数从候选集合中删除. 6)End for q 由以上算法得到的模拟预编码矩阵FRF具有如下特点: 1)FRF为NTX×NRF阶块对角稀疏矩阵(由(Q-1)个KM×K阶矩阵和1个NTX-(Q-1)KM×NRF-(Q-1)K阶矩阵顺次构成其块对角子矩阵).第nTX行仅有1个非零元素,其行维和列维分别对应于发射天线序号nTX和该天线连接的射频链路序号n=(q-1)K+koptq,nTX.第n列有M个非零元素,其行维对应于与射频链路n相连的M个发射天线的序号,且这M个非零元素构成了射频链路n(虚拟子阵列n)对应的模拟预编码向量fn.这种块对角稀疏特性使得虚拟子阵列方案符合部分连接结构. 2)FRF中各非零元素的幅度均相同,印证FRF仅涉及相位调整. 3)FRF各列的Frobenius范数均为1,印证FRF保持发射信号功率不变. 2.4 数字预编码矩阵计算 由FRF计算出等效信道矩阵G=HFRF,则迫零数字预编码矩阵可表示为[5], 由此,有 即,满足上述总发射功率的约束. 3 计算复杂度分析 比较本研究所提虚拟子阵列方案与顺序子阵列[10]、匹配子阵列[11]、分布式子阵列[12]3种传统的部分连接结构方案和全连接结构[5]方案的计算复杂度.所有方案均包含求解FRF、G和FBB3个环节.首先,在求解FRF环节,顺序子阵列[10]和全连接结构[5]方案仅需对φk,m取相反数,故相应复杂度可忽略不计.本研究所提、匹配子阵列[11]和分布式子阵列[12]3种方案则均引入了查找环节,由此增加的额外复杂度分别为OA (KM(NRF -K/2)/2)、OA ((KMNRF + DN2RFlbD/2)/2)(D表示分布阶数)和OA (MN2RFlbM/4).其次,在求解G环节,除了全连接结构[5]方案具有复杂度OM (MN3RF)之外,其他4种部分连接结构方案的复杂度均为OM (MKNRF).最后,在求解FBB环节,除了全连接结构[5]方案具有复杂度OM (N3RF)之外,其他4种部分连接结构方案的复杂度均为OM (K2NRF).表1给出了以上5种方案的总体计算复杂度.此处,脚标“A”和“M”分别表示复数加法和复数乘法.系统实现时,后者的计算复杂度大致为前者的10~100倍.综上所述,本研究所提虚拟子阵列方案相较于与顺序子阵列[10]、匹配子阵列[11]增加的计算复杂度不超过5%,与分布式子阵列[12]方案计算复杂度相当,显著低于全连接结构[5]方案. 4 仿真结果 本研究对表1所示5种方案进行了仿真评估.仿真条件和主要参数为:独立同分布Rayleigh衰落信道,即hk,nTX ~CN(0,1),且基站能获得准确下行信道矩阵H;基站天线数NTX=128,射频链路数NRF=8;分布式子阵列的分布阶数D设为能取得较好性能的4. 图2给出了用户数K=8时5种方案频谱效率与平均信噪比的关系.从图2中看出,所提虚拟子阵列方案比顺序子阵列[10]、匹配子阵列[11]及分布式子阵列[12]3种传统部分连接结构方案的频谱效率大幅提升.例如,在所示信噪比区域,所提方案相较于与其性能最接近的分布式子阵列方案[12]的频谱效率提升了约20%~80%.另一方面,所提方案相较于全连接结构方案[5]虽仍有约4 dB差距,但前者仅需128个移相器,比后者的128×8个移相器大大降低了硬件成本和功耗. 文献[5]的全连接结构方案要求用户数与射频链路数相等,而表1中其余4种部分连接结构方案均无此限制.此4种方案在平均信噪比为0 dB和10 dB时的频谱效率与用户数关系分别如图3和图4所示.由图3和图4可知:给定信噪比时,随着用户数增大,频谱效率大多展现出先升再降的特点.当平均信噪比为0 dB时,所提方案、分布式子阵列[12]、匹配子阵列[11]和順序子阵列[10]4种方案的频谱效率极大值对应的用户数分别为6、5、4和4,所提方案的频谱效率极大值分别比后三者增加了约80%、100%和120%.当平均信噪比增至10 dB时,与4种方案频谱效率极大值对应的用户数则分别升至8、8、7和6,所提方案的频谱效率极大值比后三者分别增加了约25%、40%和60%.所以,相较于3种传统方案,所提方案凭借更大空间分集增益,能通过接入更多用户以获得更高频谱效率. 上述仿真均假设移相器的相位连续可变,但实际应用时高精度移相器成本较高,因而考虑将真实相位用低成本的B比特移相器量化[5].由此,FRF各非零元素的理想相位值φ和相应量化值可用=2πm/2B,m=argminm∈{0,1,…,2B-1}|φ-2πm/2B|建立联系.图5比较了K=8时不同量化比特数对所提虚拟子阵列方案和分布式子阵列方案[12]频谱效率的影响.从图5中看出,量化比特数相同时所提方案比分布式子阵列方案[12]仍可获得约4 dB增益,且在B=3时二者都与理想相位信息的性能差距很小. 從以上独立同分布Rayleigh衰落信道的仿真可知,对用户数给定而信噪比变化及信噪比给定而用户数变化2种情形,所提方案的频谱效率相较于3种传统部分连接结构方案均有显著改善,且所提方案的性能受B比特移相器的量化精度影响较小. 5 结 论 针对部分连接结构的多用户大规模MIMO系统,本研究提出了基于虚拟子阵列的混合预编码方案.此方案在给定基站天线和射频链路数条件下,基于所提逐元最大化虚拟子阵列增益算法设计的虚拟子阵列生成器可将射频链路和发射天线更好动态匹配,从而能充分挖掘大规模MIMO的空间分集增益.复杂度分析和独立同分布Rayleigh衰落信道下仿真表明:所提虚拟子阵列方案相较于顺序子阵列、匹配子阵列、分布式子阵列3种传统部分连接结构方案,在计算复杂度略微增大的条件下能大幅增加系统频谱效率,且对移相器相位量化误差不敏感,同时,与全连接结构方案相比,以较小的性能损失大幅降低了硬件成本和计算复杂度.因此,本研究所提方案可作为大规模MIMO系统低成本低复杂度混合预编码的候选. 参考文献: [1]Marzetta T L.Massive MIMO:an introduction[J].Bell Labs Tech J,2015,20(3):11-22. [2]Alsabah M.6G wireless communications networks:a comprehensive survey[J] IEEE Access,2021,8:148191-148243. [3]范玉衡,杨闯,彭木根.感知协同太赫兹多天线移动通信:原理、现状与展望[J].移动通信,2023,47(3):84-91. [4]Molisch A F,Ratnam V V,Han S,et al.Hybrid beamforming for massive MIMO:A survey[J].IEEE Commun Mag,2017,55(9):134-141. [5]Liang L,Xu W,Dong X.Low-complexity hybrid precoding in massive multiuser MIMO systems[J].IEEE Wirel Commun Lett,2014,3(6):653-656. [6]Ioushua S S,Eldar Y C.A family of hybrid analog-digital beamforming methods for massive MIMO systems[J].IEEE Trans Sign Proc,2019,67(12):3243-3257. [7]丁青锋,罗静,高鑫鹏,等.基于混合量化移相器的毫米波大规模MIMO预编码设计[J].电子学报,2021,49(12):2349-2356. [8]肖晴,谭方青,徐超.基于人工蜂群算法的毫米波大规模MIMO 混合预编码设计[J].无线电工程,2023,53(3):584-590. [9]曾强,何雪云,孙林慧.毫米波大规模MIMO系统基于相位对齐的混合预编码方案[J].南京邮电大学学报(自然科学版),2020,40(3):46-51. [10]张雷.多用户大规模MIMO中部分连接结构的混合预编码[J].成都大学学报(自然科学版),2020,39(3):272-277. [11]张雷,高俊枫,向博.最大化子阵列增益的多用户大规模MIMO混合预编码[J].电讯技术,2021,61(9):1073-1079. [12]张雷,王勤.多用户大规模MIMO中部分连接结构的混合预编码[J].通信学报,2022,43(1):104-116. (实习编辑:黄爱明) Hybrid Precoding Based on Virtual Subarray for Multiuser Massive MIMO Systems ZHANG Lei,GAO Junfeng,XIANG Bo (School of Electronic Information and Electrical Engineering,Chengdu University,Chengdu 610106,China) Abstract:In order to obtain more spatial diversity gain in multiuser massive multiple-input multiple-output (MIMO) systems,a hybrid precoding scheme based on virtual subarray (VSA) for partially-connected structure (PCS) is proposed in this paper. The scheme allows the RF chain to be connected with the transmitting antennas dynamically. The analog precoding matrix is firstly designed by extracting the conjugate phase of the air interface channel,and an algorithm maximizing the VSA gain element-by-element is proposed to obtain greater analog precoding gain. Then a zero-forcing digital precoding is performed for the equivalent channel. Simulation results show that the VSA scheme achieves much higher spectral efficiency than the conventional PCS ones in Rayleigh fading channels,and is also insensitive to the phase quantized error. Key words:hybrid precoding;massive MIMO system;partially-connected structure;virtual subarray

