空间多观测样本的地理加权回归模型❋

栗春晓, 李芙蓉

(中国海洋大学数学科学学院, 山东 青岛 266100)

随着卫星遥感、地理信息系统和计算机技术不断发展,空间数据被广泛应用于生态学、林业、医学和海洋科学等各领域。空间数据具有空间异质性,这意味着随着地理位置的变化,变量间的关系或结构会发生变化,这种空间异质性普遍存在于空间数据中。例如,日常生活中房价及其影响因素的关系在不同区域具有明显的差异;海洋科学研究发现温度和盐度的关系随着地理位置和深度而变化[1]。在这种情况下,普通最小二乘回归(Ordinary least squares regression,OLSR)不能准确、全面地描述空间数据的真实特征,因为该模型是全局模型,没有考虑地理位置的影响,得到的结果只是所研究区域的一种平均值[2-3]。

为了进一步研究空间数据的特性,Brunsdon等[2]基于变系数回归模型提出了地理加权回归(Geographically weighted regression,GWR)模型。该模型在估计某个空间点上的回归系数时,可以利用其邻近空间点上的观测样本信息(每一空间点仅有一个观测样本),并按照距离地远近施以不同的权重来进行估计,这克服了传统回归模型的回归系数为常数的缺点[3]。在过去20年中,GWR成为探索空间非平稳关系的重要工具,被广泛用于生态学、林业、房地产等领域[4-9]。然而,GWR模型也存在很多局限性,例如,缺乏统一的方法来估计局部系数,离群值的强烈影响,弱数据问题等[10-11]。

为了克服GWR模型的局限性,学者们也提出了多种改进方法。Lesage[10,12]借助于贝叶斯方法提出了贝叶斯地理加权回归模型(Bayesian geographically weighted regression,BGWR),Charlton[13]提出了同时包含全局变量和局部变量的混合地理加权回归模型(Mixed geographically weighted regression,MGWR),Huang等[14]提出了时空地理加权回归模型(Geographi-cally and temporally weighted regression,GTWR),假设回归系数是变系数回归模型中地理位置和观察时间的函数。研究发现,这些关于GWR模型以及GWR改进模型的研究都是基于每个空间点上仅有一个观测样本的情况。然而,在实际应用中,不同的空间位置上往往有多个观测样本。例如,在研究海表面热通量与中尺度涡旋所携带的海表面温度异常关系的季节变化时,同一季节不同年份的数据就可以视作多个观测样本;在研究不同普查区域家庭收入与学龄儿童体重指数(BMI)的关系时,同一普查区域不同儿童的数据同样可以视作多个观测样本。

当每个空间点上的观测样本数量相同时,一种可能的策略是分别对每组观测样本(这里定义所有空间点上的一次观测为一组观测)利用GWR模型对回归系数进行估计,再对基于每组观测样本得到的回归系数求平均数或中位数,从而得到最终回归系数的估计。然而,该想法忽略了每组观测样本所得回归系数都应相同这一事实。此外,当每个空间点上的样本数量不一样时,甚至无法定义一组观测样本,使得已有的GWR模型根本无法应用。另一种可能的策略是对每个点上的所有观测样本分别进行普通最小二乘回归,但这未能利用回归关系在邻近的空间点上具有相近值这一特点,导致估计效果不理想。特别的,当每个空间上的样本数量较少时,会导致严重的估计误差。

鉴于此,本文对经典GWR模型进行拓展,构建了一种可以处理空间点上任意样本数量的地理加权回归模型(Multiple-replicate geographically weighted regression,MRGWR)。MRGWR模型在估计回归系数时,充分利用了回归关系在邻近点上具有相似性的特点,并对邻近空间点的观测样本施加不同权重。本文进一步基于数值仿真实验与实证研究,对模型的有效性与适用性进行了分析。

1 模型

1.1 GWR模型

假设(ui,vi)是第i个空间点位置,{(yi,xi),i=1, 2, …,n}是观测样本在观测位置(u1,v1)、 (u2,v2), …, (un,vn)处的观测值,xi=[xi1,xi2, …,xip]T表示观测位置(ui,vi)处的p维解释变量,yi为对应的响应变量。将经典OLSR模型推广到空间上,则GWR模型可写成

(1)

式中:βik表示第k个解释变量在(ui,vi)处所对应的回归系数;εi为独立同分布的白噪声过程均值为0,方差为σ2。对于GWR模型,βi=[βi1,βi2, …,βip]T的估计值为

(2)

其中,

Wi=W(ui,vi)为n×n空间权重矩阵,其对角线元素wij表示观测点i与观测点j之间的核函数,wij与点i到点j的空间距离相关。

1.2 MRGWR模型

模型(1)假定在每一个空间点(ui,vi)上,仅有一个观测样本(yi,xi),然而,在许多空间数据集中,不同的空间位置上往往有多个观测样本。考虑下面这种情况,空间点(ui,vi)上具有hi个观测样本,样本观测值为

(yi1;xi11,xi12, …,xi1p), (yi2;xi21,xi22, …,xi2p), …, (yihi;xihi1,xihi2, …,xihip)。

其中,(yil;xil1,xil2, …,xilp),l=1, 2, …,hi是观测点在(ui,vi)处响应变量和解释变量的第l个观测值,i=1, 2, …,n。

此时,模型(1)需改写为

(3)

MRGWR模型作为GWR模型的推广,沿用了GWR模型中最基本的思想,即估计(ui,vi)处的回归系数时,可以利用其邻近空间点上的观测样本信息,并按照距离地远近施以不同的权重来进行估计。在MRGWR模型中,回归系数的估计值应使得以下加权残差平方和取得最小值

(4)

其中,wij为估计(ui,vi)处的回归系数时,(uj,vj)处的观测样本所被赋予的权重。wij与(ui,vi)和(uj,vj)之间的距离有关,其具体表达式将在1.3节详细说明。需要指出的是,wij与样本本身无关,同一点上的不同样本被赋予同样权重。

公式(4)可以写成以下矩阵形式:

其中,

Wij=diag[wij,…,wij]hj×hj,

X=[X1,X2,…,Xj,…,Xn]T,

y=[y11, …,y1h1, …,yn1, …,ynhn]T,βi=[βi1,βi2, …,βip]T,Wij是(ui,vi)处观测样本与(uj,vj)上hj个观测样本之间地理距离的空间权重矩阵。

由此解出空间点(uj,vj)上的回归系数为

(5)

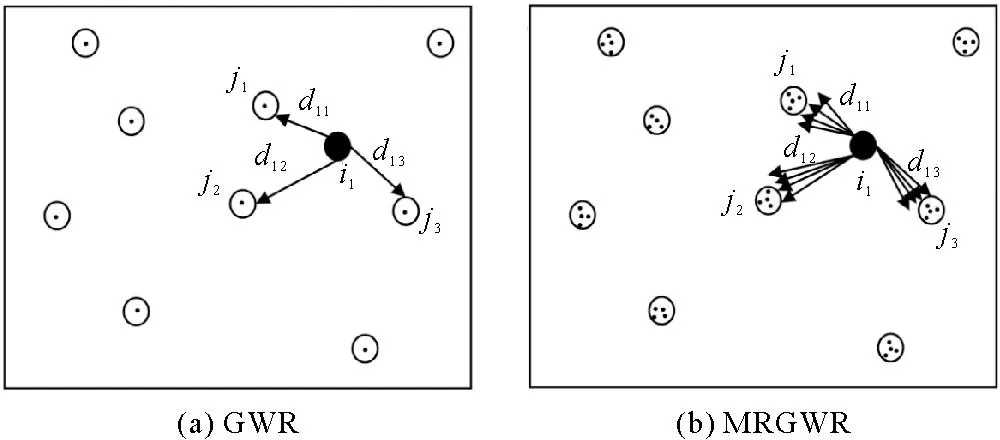
图1 GWR模型(a)和MRGWR模型(b)的估计原理示意图Fig.1 Schematic of GWR model (a) and MRGWR model (b) estimation principles

1.3 核函数和带宽

符合以上要求的空间核函数类型较丰富。常用的函数类型包括Gauss核函数、Exponential核函数、Bi-square核函数、Tri-cube核函数等[15]。在本文中,采用的是Exponential核函数,其表达式为

wij=exp(-‖dij‖/b)。

(6)

其中,b为带宽参数,控制着权重随着距离增加的衰减速度,其大小决定了拟合曲面的光滑性。

与核函数的选择相比,回归系数对于带宽的选择表现得更敏感,带宽过大回归系数估计的偏差过大,带宽过小又会导致回归系数估计的方差过大。因此,选取合适的带宽参数对于MRGWR模型估计的准确性至关重要。目前,常用的最优带宽选取准则有交叉验证方法(CV)、广义交叉验证方法(GCV)以及修正的赤池信息准则(AICC)[16-19]。本文采用CV方法,如果有需要的话,也可以直接采用其他准则。

2 数值仿真实验

本节通过数值仿真实验来评估普通最小二乘回归,GWR和MRGWR模型在不同情况下的估计性能。

2.1 实验设计

模拟实验中,选取平方域[0, 1]×[0, 1]构成地理区域,从中随机生成500个空间位置,每个位置上的响应由下式产生:

yil=βi1xil1+βi2xil2+βi3+εil。

(7)

在以往的数值实验模拟中,解释变量的值通常从白噪声过程中产生[20-21]。在海洋科学的许多应用中,用于拟合回归模型的解释变量具有明显的空间结构[22]。因此,为了模拟实际情况,在数值实验中基于空间过程生成解释变量。具体来说,先定义{z1(ui,vi)}和{z2(ui,vi)},i=1, 2, …, 500是服从空间高斯过程的两个独立观测,且其均值为零,变量协方差矩阵定义为

在数值实验中,回归系数被设计成具有空间上连续变化的形式,并由一个空间高斯过程生成。具体而言,βi=[βi1,βi2,βi3]服从空间高斯分布过程,且均值为0,协方差矩阵由一个各向异性的指数函数定义

Cov(βik,βjk)=

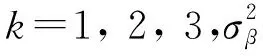
基于以上模型,设计以下三组实验来评估所建立的MRGWR、GWR和OLSR模型系数估计的性能。

实验1:解释变量具有不同的空间自相关性。在研究中设定σ=1,h=10,φ=[0.1, 0.3, 1]。

实验2:空间点上具有不同的观测样本数量。在研究中设定σ=1,φ=0.3,h=[3, 10, 30]。

实验3:回归模型具有不同的信噪比。在研究中设定h=10,φ=0.3,σ=[0.3, 1, 3]。

每组实验均开展100次数值模拟来评估不同模型的估计效果。为了量化每种模型估计的性能,引入估计的均方误差(MSE),并定义为

(8)

2.2 实验结果分析

2.2.1 解释变量具有不同的空间自相关性 在实验1中,通过设定φ=[0.1, 0.3, 1]来改变解释变量的空间自相关性,进而评估在不同φ值下回归模型的估计性能。图2展示了回归系数的真值以及当φ=0.3时,OLSR、GWR和MRGWR三种模型的估计结果。其中,GWR模型的回归系数估计值是基于每组观测样本得到的回归系数求平均得到的(定义所有空间点上的一次观测为一组观测)。

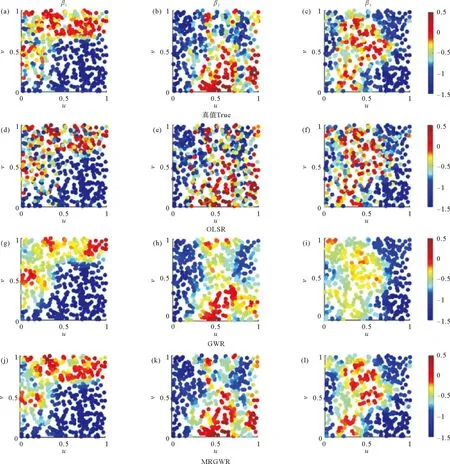
((a)—(c)回归系数β1、β2和β3的空间结构;(d)—(f)OLSR模型的估计结果;(g)—(i)GWR模型的估计结果;(j)—(l)MRGWR模型的估计结果。该模拟中,空间自相关性φ=0.3, 观测样本数量h=10, 标准差σ=1,右侧图示表示回归系数的大小。(a)—(c) denote the spatial structure of the regression coefficients β1、β2 and β3; (d)—(f) denote the estimation results of OLSR model; (g)—(i) denote the estimation results of GWR model; (j)—(l) denote the estimation results of MRGWR model. In this simulation, spatial autocorrelation φ=0.3, number of replicates h=10, standard deviation σ=1, right-hand icons indicate the magnitude of the regression coefficients.)图2 回归系数估计值对比Fig.2 Comparison of regression coefficient estimates

从图2可以看出,MRGWR估计的回归系数与真实值更加一致, GWR和OLSR模型估计的回归系数与真实值差异较大。一方面,OLSR模型未能利用回归关系在邻近的空间点上具有相近值这一特点,导致估计效率果不理想。另一方面,尽管GWR模型利用了空间相邻点的观测信息,但它忽略了对于每组观测样本回归系数都是相同的这一事实。相反,MRGWR模型估计结果更准确,因为它充分利用了回归关系在邻近点上具有相似性的特点,并对邻近空间点的观测样本施加不同的权重。

表1展示了MRGWR、GWR以及OLSR模型在解释变量具有不同强度的空间自相关性之下回归系数的估计误差。由表1可知,在解释变量具有三种强度的空间自相关性下,GWR和MRGWR模型的估计性能均显著优于OLSR模型,且MRGWR模型的估计性能相比于GWR模型更优。随着空间自相关性增强(即φ不断增大),OLSR和GWR的估计误差逐渐变大,虽然MRGWR的估计误差也在变大,但幅度很小,其值远低于OLSR和GWR的估计误差。这说明当解释变量存在强空间自相关性时,MRGWR相对于GWR估计效率上的优势更加突出。例如当φ=0.1时,MRGWR模型的MSE约为GWR模型的1/2;但当φ=1时,MRGWR模型的MSE仅为GWR模型的1/4。

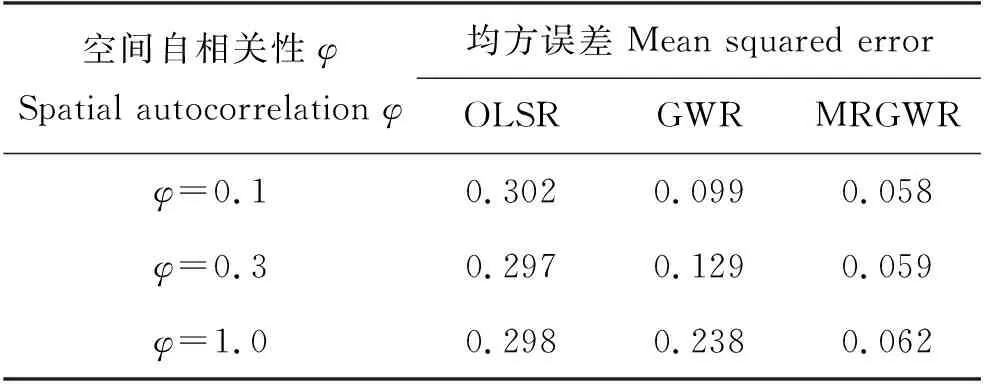
表1 不同解释变量间自相关性下各模型100次模拟的平均均方误差Table 1 Average mean squared error for 100 simulations of each model under different spatial autocorrelation in the explanatory variables

2.2.2 不同的观测样本数量 在实验2中,我们通过设定h=[3, 10, 30]来评估不同模型在空间点上不同观测样本数量下的性能,表2比较了三种模型在100组模拟下的平均MSE。

由表2可知,对于空间点上各种观测样本数量,MRGWR均保持较低的误差,且都优于OLSR和GWR模型。此外,随着h值的减少,三种模型的MSE都变大,估计性能随之降低,这种退化对OLSR来说是最严重的,但对GWR和MRGWR来说MSE的变动幅度要小很多,因为它们利用的是邻近的观测样本。在h=3或10时,虽然GWR要显著优于OLSR,但当h=30时,OLSR却更优于GWR,而MRGWR模型的MSE都小于OLSR模型。由此可见,相比于OLSR和GWR模型,MRGWR模型表现更优。

表2 不同的观测样本数量下各模型100次模拟的平均均方误差Table 2 Average mean squared error for 100 simulations of each model under different number of replicates

2.2.3 不同的信噪比 在实验3中,我们通过设定标准差σ=[0.3, 1, 3]来改变回归模型的信噪比,进而评估三种不同信噪比设置下回归模型的性能。表3比较了三种模型在100组实验下的平均MSE。从表3中可以看出,对于模型的各种信噪比,MRGWR模型的估计性能总是显著优于OLSR和GWR模型。此外,随着σ值从0.3变为1或3,模型信噪比从较高水平变为中等水平或较低水平,OLSR的MSE大幅增加,且波动幅度较大,而MRGWR和GWR模型的MSE增幅较小。特别的,当σ=0.3时,GWR模型的MSE大于OLSR,但当σ=1或3时,结果相反。相比之下,在所有三种情况下,MRGWR估计的MSE总是小于OLSR估计的MSE,且MRGWR的分布较为集中。

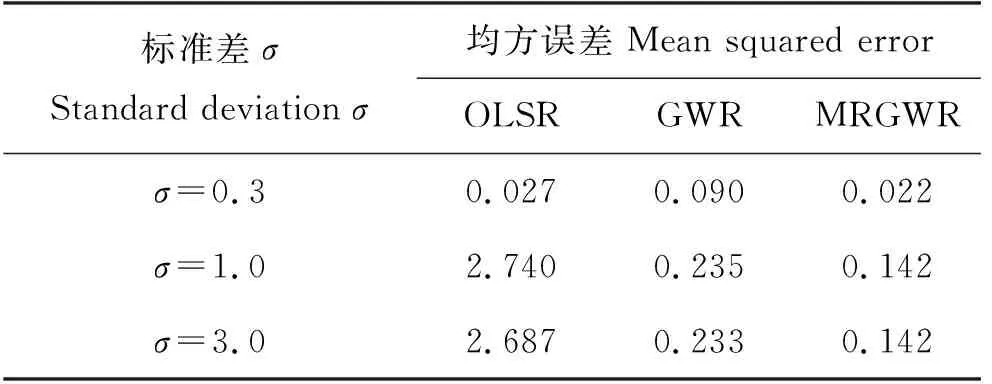
表3 不同的标准差下各模型100次模拟的平均均方误差Table 3 Average mean squared error for 100 simulations of each model under different standard deviation

2.3 数值仿真实验总结

为了检验模型在不同情况下的估计性能,本文分别从解释变量的空间自相关性、空间点上观测样本数量以及模型信噪比三个方面展开具有空间结构的数值仿真实验。结果表明,无论解释变量的空间自相关性、观测样本数量以及模型信噪比如何变化,MRGWR模型的估计性能总是优于普通最小二乘回归和GWR模型。特别是当解释变量在空间上高度相关、观测样本数量较少、模型信噪比较低时,普通最小二乘回归和GWR模型的估计性能会存在不同程度上恶化。相比之下,MRGWR模型在这种情况下仍能产生合理的估计,表明其具有较强的稳健性。

3 实际应用

3.1 问题背景

中尺度涡旋占据了海洋中90%的动能,是海洋上层最显著的运动形式,对海洋中热量、溶解气体以及营养物质的输送起着重要的作用[23]。传统的中尺度涡旋研究主要是从海洋自身的动力过程出发,缺少对涡旋与大气间相互作用的考虑[24-26]。然而,近十几年的观测和数值模拟结果表明海洋中尺度涡旋与大气之间存在着强烈的相互作用,反过来可以给海洋中尺度涡旋带来反馈[27-30]。因此,中尺度涡旋与大气相互作用已经成为当前物理海洋和气候研究的一个前沿领域。

中尺度涡旋与大气之间存在多种形式的相互作用。特别是中尺度涡旋携带的海表面温度(Sea surface temperature,SST)异常可以对海气界面的热通量产生强烈的影响[1,29,31-32]。也就是说,暖(冷)异常会促进(抑制)热量从海洋进入大气。除了极大地影响大气边界层的动态过程外[33-34],这种中尺度涡旋引起的海面热通量异常反过来又抑制了中尺度SST异常,成为涡旋势能耗散的重要途径[29],这一过程被称为涡旋热反馈[35]。涡旋热反馈的强度可以通过中尺度海面热通量异常对中尺度SST异常的回归系数来衡量。然而,由于这种回归关系受到背景大气的动力和热力学结构的调控,存在明显的季节性和空间差异,因此难以通过经典的OLSR模型进行估计。

鉴于此,本文通过MRGWR模型来估计中尺度SST异常与海面净热通量异常间(本文中的热通量定义向上为正)的回归关系,进而揭示中尺度海面净热通量异常对中尺度SST异常的响应关系随季节和空间的变化特征。

3.2 数据来源

本节数据来自第三代日本海洋通量数据集(J-OFURO3),包含1988—2017年(30年)的SST和海面净热通量的月平均场,水平空间覆盖的范围为全球海域(90°S—90°N,180°E—180°W),可通过以下网址下载:https://j-ofuro.isee.nagoya-u.ac.jp/en/dataset/entry-114.html。该数据的空间分辨率为0.25°×0.25°,能够分辨出大部分中尺度涡旋引起的SST异常。为了提取中尺度SST和海面净热通量异常,我们首先对原始数据进行4°×4°的空间滑动平均,并剔除该滑动平均的信号,将剩余的异常场定义为中尺度异常。

为了能够较好表征中尺度涡旋热反馈,本文选取北太平洋(10°N—65°N,105°E—90°W)为研究区域,见图3红色矩形区域。

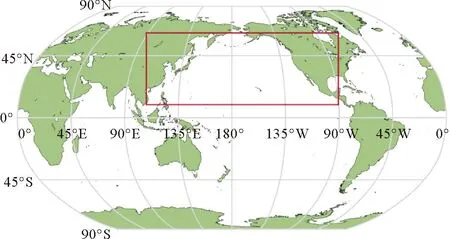
(红色矩形为研究区域,白色为海域。Red rectangle is the study area, white is the sea area.)图3 实验海域Fig.3 Experimental sea area

3.3 模型应用

由于本文关心的是中尺度海面净热通量异常对中尺度SST异常的响应关系随空间和季节的变化,所以对于不同月份(1月、2月……12月)的数据分别利用MRGWR模型进行估计,并将不同年份同一月份的数据视作多次观测,即每个月每个空间点上都有30次观测样本。在此假定下,对于每个月,可建立如下回归模型

Qil=βi1Til+βi0+εil。

式中:Qil表示在位置点(ui,vi)上第l年的中尺度海面净热通量异常;Til表示在位置点(ui,vi)上第l年的中尺度SST异常;βi1是这两个变量之间的空间回归系数,用于描述中尺度海面净热通量异常对中尺度SST异常的响应关系;βi0是空间回归模型的截距;εil表示随机误差项。为了降低计算负担,在北太平洋海域非零的观测值地理位置中,随机选取10 000个点进行估计。

图4展示了由MRGWR模型估计得到的中尺度海面净热通量异常与中尺度SST异常之间的空间回归系数β1的季节和空间的变化特征。从空间上来看,中尺度海面净热通量异常对中尺度SST异常的响应存在显著的南北向差异,在副热带海区β1可达60～70 W/(m2·K),而在副极地海区β1则只有40 W/(m2·K)左右。此外,β1在黑潮延伸体区域呈现出局地增强特征。这些空间特征背后的物理机制值得相关领域的学者深入分析。在季节变化方面,β1整体呈现冬强夏弱的特征,这种季节变化在中高纬度要比低纬度更明显。由于海气间的热量交换显著依赖于海表面风速,因此中高纬度冬季的β1大概率是由冬季风暴过程所引起的较强风场导致的,但是否还有其他控制因素还需要进一步分析。综上所述,中尺度海面净热通量异常对中尺度SST异常的响应关系存在显著的季节和空间变化特征,MRGWR模型提供了一种可靠的提取该特征的统计方法。

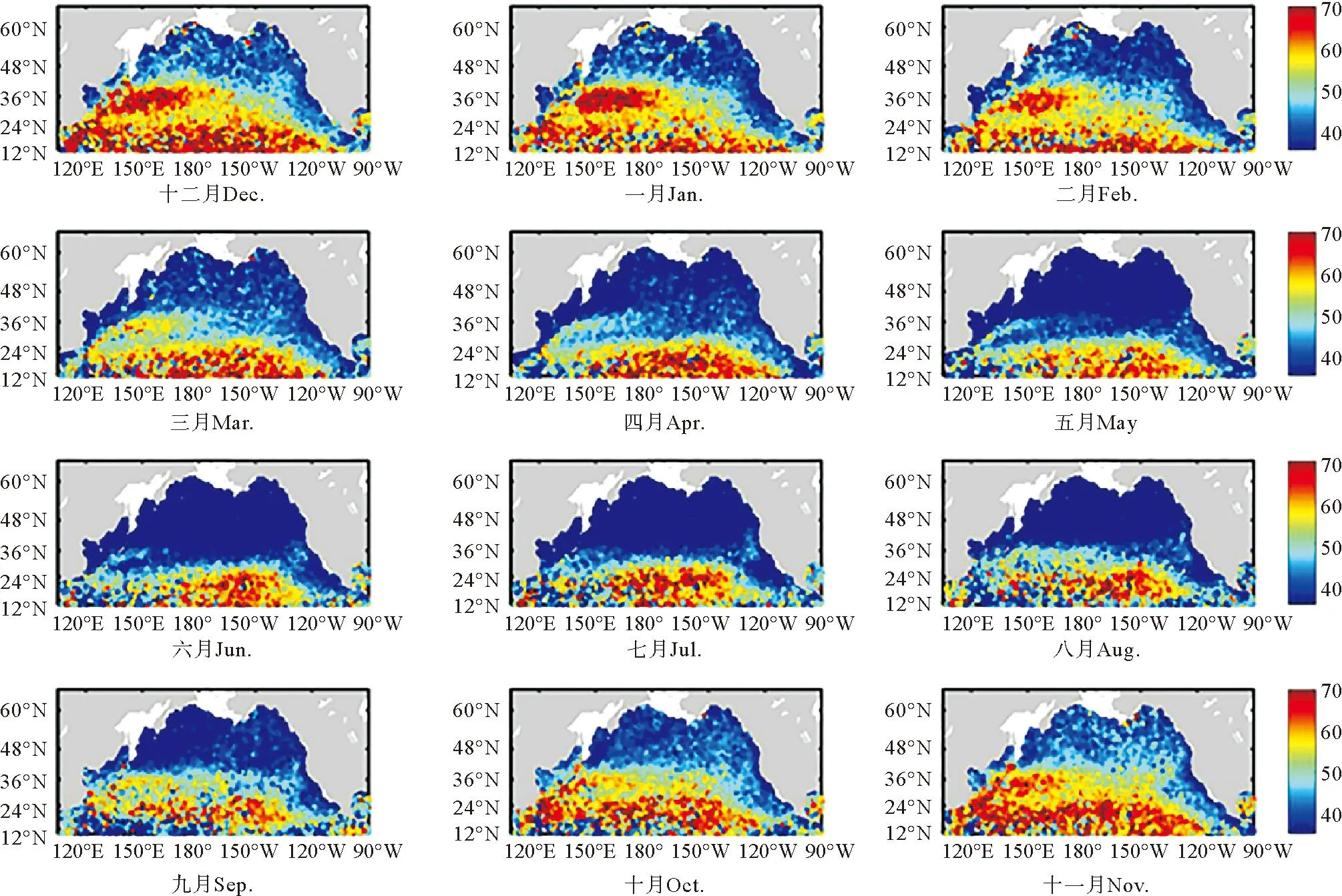
(右侧图示表示β1的大小,单位为W/(m2·K)。陆地被灰色掩盖。Right-hand icons indicate the magnitude of β1 in W/(m2·K).Land is masked by grey.)图4 不同月份下β1的空间分布Fig.4 Spatial distribution of β1 for different months

4 结语

本文针对现有的GWR模型以及GWR改进模型无法处理空间点上多个样本的情形,对GWR模型进行了拓展,构建了一种可以处理空间点上任意样本数量的地理加权回归模型——MRGWR。MRGWR模型在估计回归系数时,充分利用了回归关系在邻近点上具有相似性的特点,并对邻近空间点的观测样本施加不同权重。通过开展数值仿真实验,评估了在不同的解释变量空间自相关性、不同的观测样本数量以及不同的模型信噪比下,MRGWR模型的估计性能。数值实验结果表明,与普通最小二乘回归和GWR模型相比,MRGWR模型能够有效地处理空间点上有多个观测样本的情形,且估计性能总是优于普通最小二乘回归和GWR模型。本文进一步将MRGWR模型用于探究北太平洋中尺度海面净热通量异常对中尺度SST异常的响应关系,研究发现,中尺度海面净热通量异常对中尺度海面温度异常的响应关系存在显著的正相关以及明显的空间和季节变化。