基于改进残差网络的大地电磁反演研究
李思平,刘彩云,熊杰,田慧潇,王方
(1.长江大学 电子信息学院,湖北 荆州 434023;2.长江大学 信息与数学学院,湖北 荆州 434023)
0 引言
大地电磁测深是以天然交变电磁场为场源来研究地球内部电性结构的一种重要的地球物理勘探方法,其反演问题一直是地球物理工作者研究的重点[1]。常用的反演方法,如OCCAM反演[2]、快速松弛RRI反演[3]、自适应正则化反演[4]等在大地电磁数据处理中占有重要席位,然而这些方法都受非线性和非唯一性的限制,在计算过程中要依赖先验信息和初始模型的选择,且有陷入局部极小的风险。随着地球物理反演方法的发展,差分进化法(DE)[5]、蚁群算法(ACO)[6]和人工神经网络[7]等全局寻优的反演方法进入人们的视野,这些方法不依赖于初始模型,但存在反演时间长、计算量大的问题,且针对二维反演或三维反演,效果还有待改进。
与以上反演方法相比,基于深度学习(DL)的完全非线性反演方法无需计算偏导数和灵敏度矩阵,对初始模型依赖性小且具有良好的全局寻优性能,因此在地球物理数据处理中受到极大关注。例如:Noh等[8]采用深度神经网络(DNN)对一维的频率域航空电磁数据进行了反演,相比于高斯-牛顿反演方法,尽管合成的训练集数据量较少,其结果仍然具有较高的分辨率;Liu等[9]提出了一种基于深度残差网络(ResNet18)的一维音频大地电磁反演方法;Wang等[10]实现了基于深度置信网络(DBN)的大地电磁测数据的二维非线性反演;廖晓龙等[11]提出一种基于卷积神经网络(CNN)的大地电磁反演方法;范振宇[12]以深度残差网络(ResNet50)为基础,实现了大地电磁反演并解决了实测问题。上述反演方法均克服了传统方法的不足且在一定程度上提高了大地电磁反演的计算效率,但也存在一定的问题,例如在二维反演方面,有的网络结构简单[11],受到网络层数的限制导致表达能力有限,反演准确性、探测深度和纵向分辨率有待进一步提高,并且理论模型反演的视电阻率数据都是“学习”过的,对于未“学习”过的数据,其反演效果(即泛化能力)如何值得进一步研究;有的可以解决大尺度实测数据反演问题,但“以分类替代回归解决实际问题,无法完全提取数据的特征与标定电阻率值精细拟合”[12]。
因此,本文提出一种改进的残差网络(iResNet),通过对多种二维地电模型进行网络学习训练和反演测试,并将反演结果与CNN网络进行对比,验证该网络对大地电磁非线性反演的可行性和准确性,评估网络的泛化能力和抗噪声能力,最终应用于实测数据解决实际问题。
1 方法原理
1.1 卷积神经网络
卷积神经网络(CNN)是深度学习的代表算法之一, 可实现卷积计算。基础的卷积神经网络由卷积层、池化层、全连接层三种结构组成,网络结构如图1所示。
图1 卷积神经网络[13]
对于卷积神经网络而言,网络越深准确率越高,然而过深的网络不仅容易出现梯度消失和梯度爆炸的问题,还会出现“退化现象”,即当网络达到一定的深度后继续增加层数,模型的准确率却会下降。于是He等学者提出了残差网络[14]。残差网络不仅可以有效地解决神经网络中梯度爆炸和梯度消失的问题,还通过引入“快捷连接”来解决 “退化现象”。“快捷连接”能将输入x添加到经过两个权重层之后的输出中,如图2所示,因此输出H(x)等于输入的映射F(x)加上输入x,该模型即为残差模块。
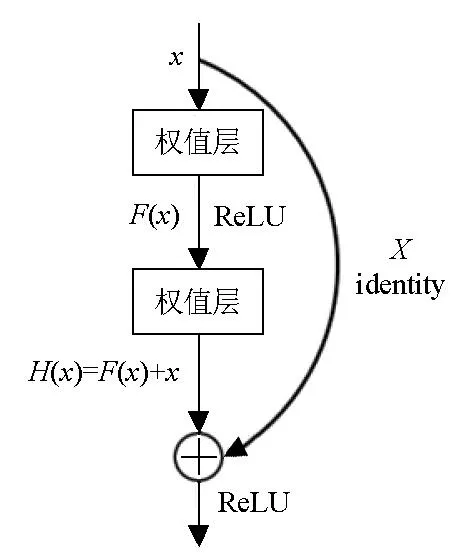
图2 残差网络的一般结构Fig.2 General structure of ResNet
残差网络采用的不是直接学习堆叠网络的潜在映射H(x),而是增加一个恒等映射来拟合残差映射F(x)=H(x)-x,F(x)包含2个权值层和1个ReLU(linear rectification function),易于优化。具体在构造ResNet时,F(x)可以根据实际要求采用不同的残差块。如图3展示的两种典型的残差结构,基于基本块(residual block)和基于瓶颈块(bottleneck block),用于构建基于深度卷积网络的ResNet。其中,n、i分别表示经过1×1或2×2卷积后的特征图数量,也就是通道数量。图3a与图3b的不同在于后者具有3个卷积层,当输入与输出的维度不相同时需要用图3b来调整维度。
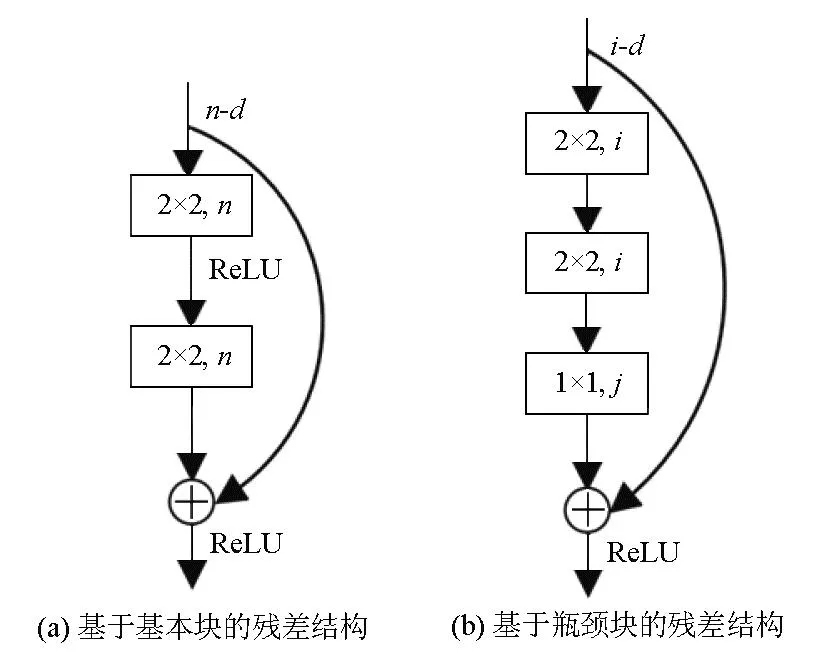
图3 两种典型的残差结构
1.2 反演原理
目前,CNN 的主要应用集中在图像识别、目标检测等领域[15],处理的目标通常是图像。在地球物理领域,利用CNN实现大地电磁二维反演时,以二维视电阻率作为输入数据,二维地电模型参数作为网络的输出,核心思想是用卷积神经网络建立从输入(视电阻率)到输出(地电模型)之间的映射关系,即通过求解以下优化问题来实现。
用数学公式可以这样描述这个过程:给定一组视电阻率数据d和地电模型m,通过损失函数L去调整参数θ,最终获得参数化模型Net(d,θ)。神经网络参数更新表达式为[16]
(1)
式中:θ表示网络中需要更新的权重和偏差;Net(·)卷积神经网络表示从视电阻率数据d到预测地电模型mpred之间的映射;L是MSE损失函数。上式的意义在于优化θ,使得预测地电模型mpred和真实地电模型m之间的误差最小。
1.3 目标函数设置
本文的目标函数设置为
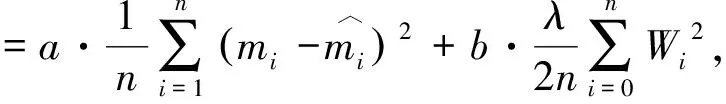
(2)
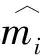
如式(2)所示,本文目标函数由两部分组成:损失函数和正则化项,其中,损失函数用来均衡模型的预测结果与真实值之间的误差;正则化项用来避免模型过拟合。具体来说,损失函数为理论模型与反演结果的均方误差,对应目标函数第一项;正则化项为网络权重约束项,对应目标函数第二项。如此设置,能使神经网络不仅拥有一定的学习能力,还能增强其泛化能力。
2 基于iResNet的大地电磁反演
2.1 反演流程
反演是由观测数据反推模型参数的映射,具体实现过程如图4所示,主要包括4个步骤:构建数据集、搭建网络、训练网络与数据反演。
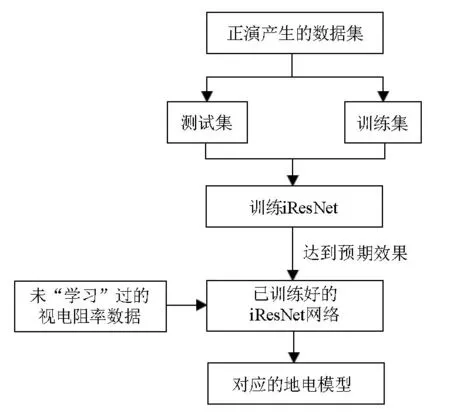
图4 反演过程
1)利用有限单元法计算不同地电模型的视电阻率,将视电阻率和模型对组成数据集,并按一定的比例分为训练集和验证集。
2)设计iResNet超参数建立网络模型,超参数主要包括:网络模型结构、卷积层、残差模块的窗口和步长等。
3)分别利用训练集和验证集对网络进行训练和测试,不断优化网络参数。
4)将未“学习”过的视电阻率数据输入到已训练好的iResNet网络,输出对应的地电模型,实现反演。
2.2 残差网络结构
通过图3所示的残差结构,本文借鉴经典的残差网络ResNet18,改进得到一种新的反演网络iResNet。该网络主要由4个残差块和2个全连接层组成,其中每个残差块由4个卷积核和2个快捷连接组成,在Block2、3、4中由于输入和输出的数据维度不同,因而第一个快捷连接的方式存在差异。网络具体参数如图5所示[9]。
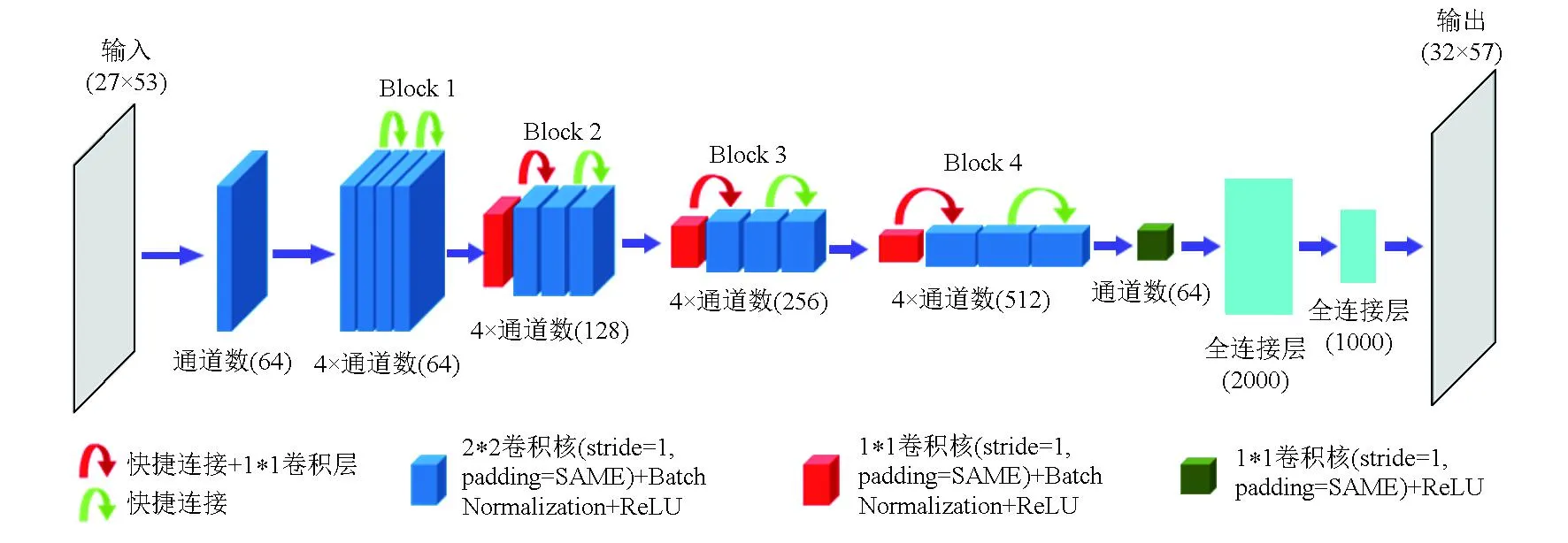
图5 iResNet网络结构[9]
3 模型试验与结果分析
3.1 数据集设置
在二维大地电磁TM极化模式下,设计了5×5(500 m×500 m)、6×6(600 m×600 m)、8×4(800 m×400 m)、4×8(400 m×800 m)、5×10(500 m×1 000 m)、10×5(1 000 m×500 m)共7个形状规则且单一的模型,以及由3个4×8堆叠的不规则梯形,并针对每种模型均设置4个阻值:高阻3 000、2 500 Ω·m,低阻500、200 Ω·m,部分模型如图6所示。
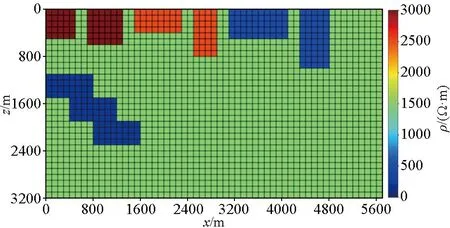
图6 模型示意
在正演过程中,有限单元法目标区域网格规模设置为32×57,网格间距为100 m。考虑到计算量的问题,异常体和围岩的电阻率值不变,只通过改变异常体位置获得用于网络训练和反演测试的二维数据,其中异常体移动位置遍布整个网格,每次移动间距为200 m,共生成8 987组数据构成数据集。计算时,选择53个测点,并记录27个频点的视电阻率。将采集范围内所有测点和频点电阻率作为网络输入,则输入为27×53的二维数据矩阵;将地电模型参数作为网络输出,则输出层神经元个数为32×57。
3.2 数据预处理
对上文中获得的数据集进行归一化处理。数据的归一化操作可有效提升网络训练效率,避免梯度爆炸的产生。采用线性函数归一化方法实现样本数据的归一化,将数据归一化到[0,1],其表达公式为
(3)
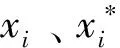
3.3 验证集反演结果
在TM模式下,对上文3.1节中的模型进行反演测试。通常,训练集用于训练网络的权重与偏差,而验证集用于验证训练后网络的准确性。在本文中,对于iResNet网络,一共有8 987组数据样本,随机抽取90%(8 088组)作为训练集,剩下10%(899组)作为验证集。表1为训练网络时的参数设置。
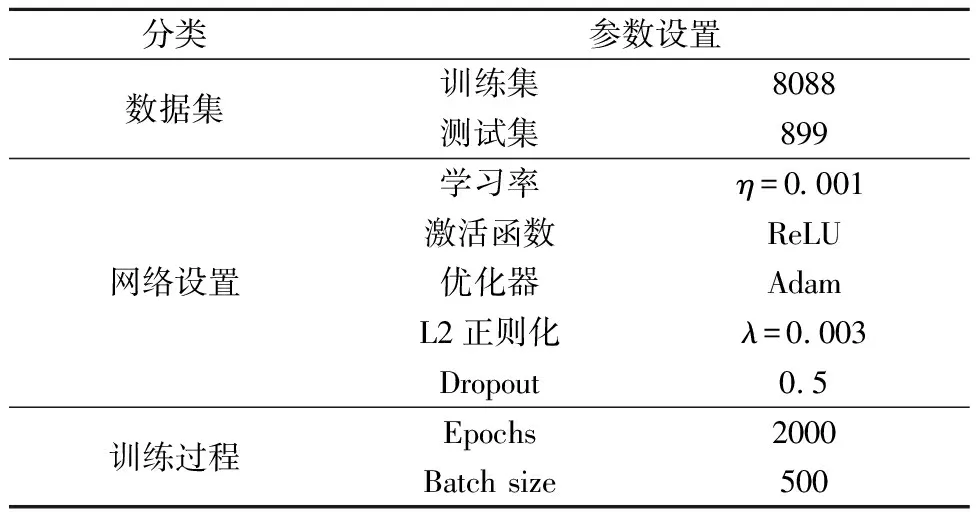
表1 iResNet网络参数设置
通过调整参数进行迭代训练。图7给出了随机抽取的几组反演结果,可以看出:iResNet网络反演精度较高,能准确反演出模型的具体位置、形状以及电阻率值,且反演精度受探测深度影响较小,具有较好的纵向分辨率。
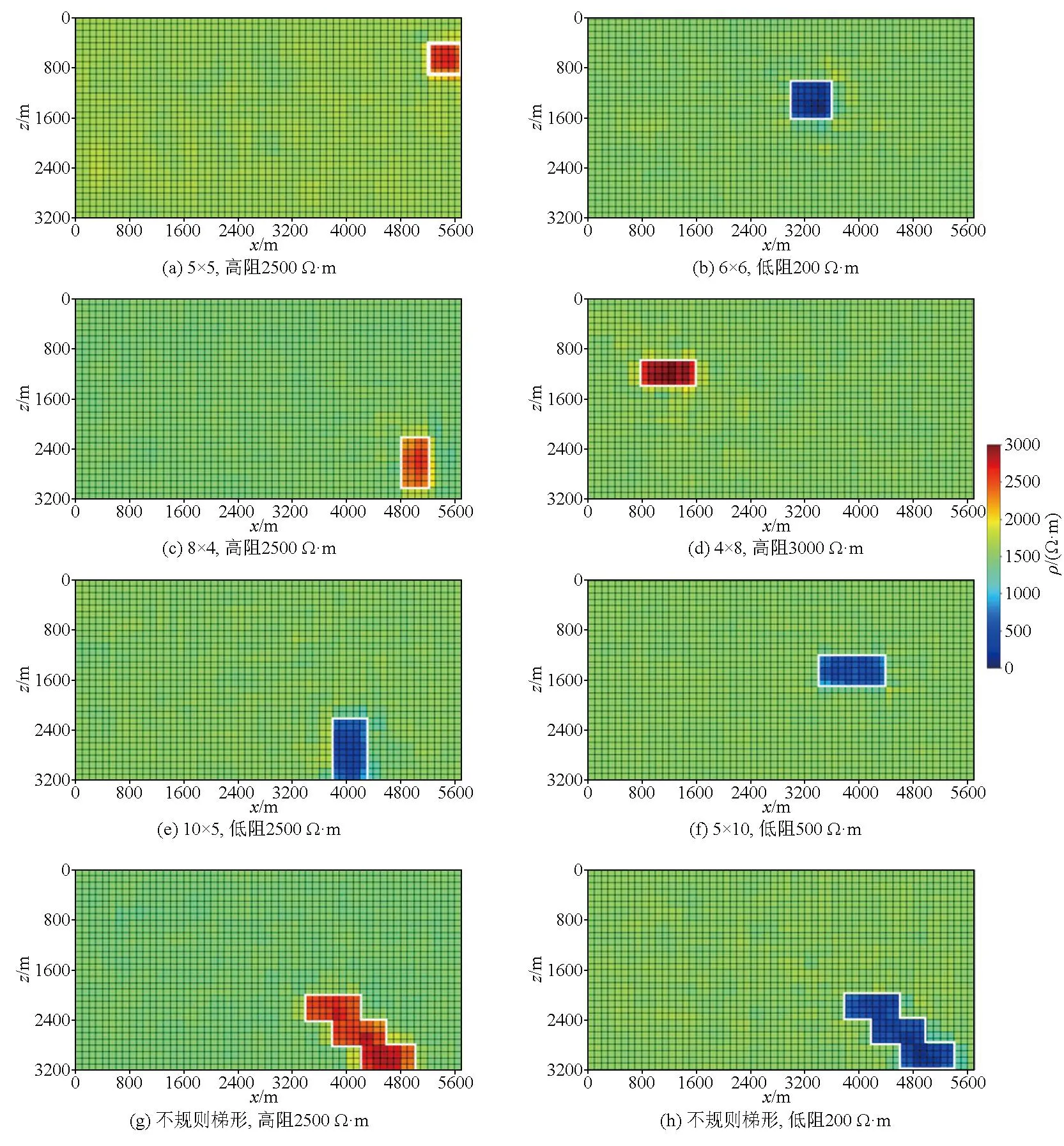
图7 部分验证集样本的反演结果
3.4 与CNN反演结果对比
图8为廖晓龙等[11]用CNN网络得到的反演结果,其中用于反演的低阻异常体电阻率为100 Ω·m,形状为5×5(1 km×1 km),背景电阻率为1 000 Ω·m;地堑模型凹陷部分电阻率为100 Ω·m,长度为6格(1.2 km),宽度为11格(2.1 km);基底电阻率为1 000 Ω·m。在保持背景电阻率、异常体形状及电阻率均与上述参数相同的情况下,本文使用iResNet网络的反演结果如图9所示。对比来看,CNN网络得到的反演模型随着所处位置的加深,其形状逐渐模糊且边缘电阻率值与真实值相差较大,而本文使用的iResNet网络得到的反演模型其形状以及电阻率值不会受到深度的影响,在反演准确性、探测深度和纵向分辨率方面均优于CNN网络。
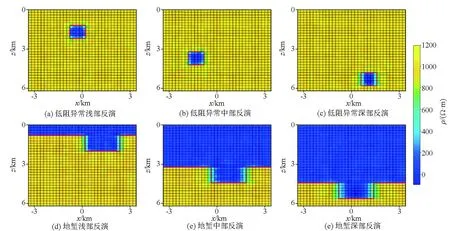
图8 CNN的反演结果[11]
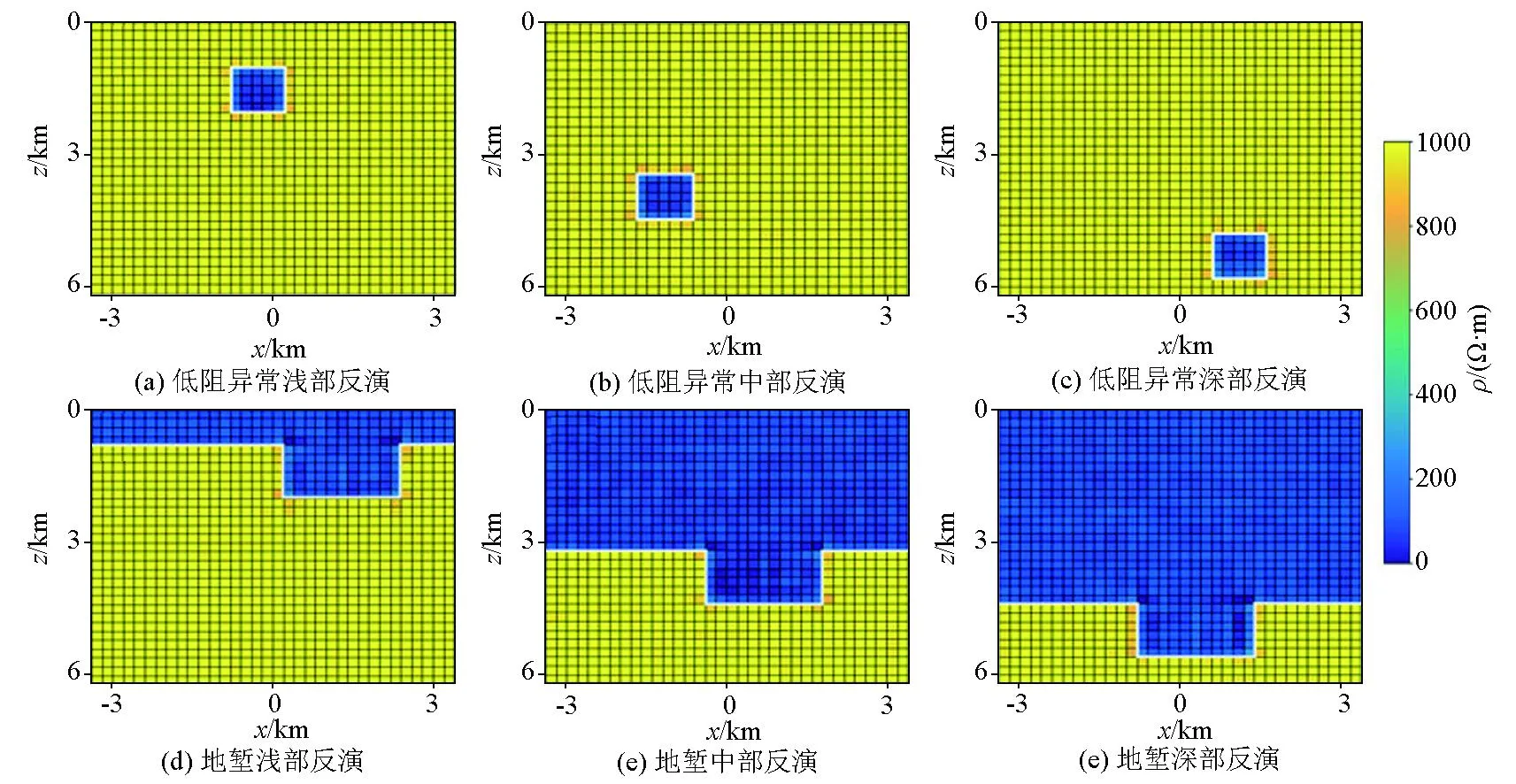
图9 iResNet的反演结果
3.5 泛化能力测试
由于训练集和验证集中的模型形状和电阻率值都是已“学习”过的,所以验证集的反演结果只能用来评估网络的质量,而不能评估网络的泛化能力。因此本文设计了多个未“学习”过的模型来评估iResNet网络的泛化能力。
3.5.1 实验一
采用“学习”过的电阻率参数(3 000、2 500、500、200 Ω·m)搭配未“学习”过的形状(6×12、7×7、4个4×8堆叠的不规则梯形)构成测试集来进行评估。随机抽取几组反演结果,根据图10a~d中单一规则模型的反演结果来看,反演得到的模型其位置与真实模型基本一致,模型四周少量单元格的电阻率值与实际值存在差异,但均可较好地确定模型的整体形状;图10e~f中,4个4×8堆叠的不规则梯形反演结果的位置及形状几乎与真实模型一致,少许单元格的电阻率值略低于实际值。
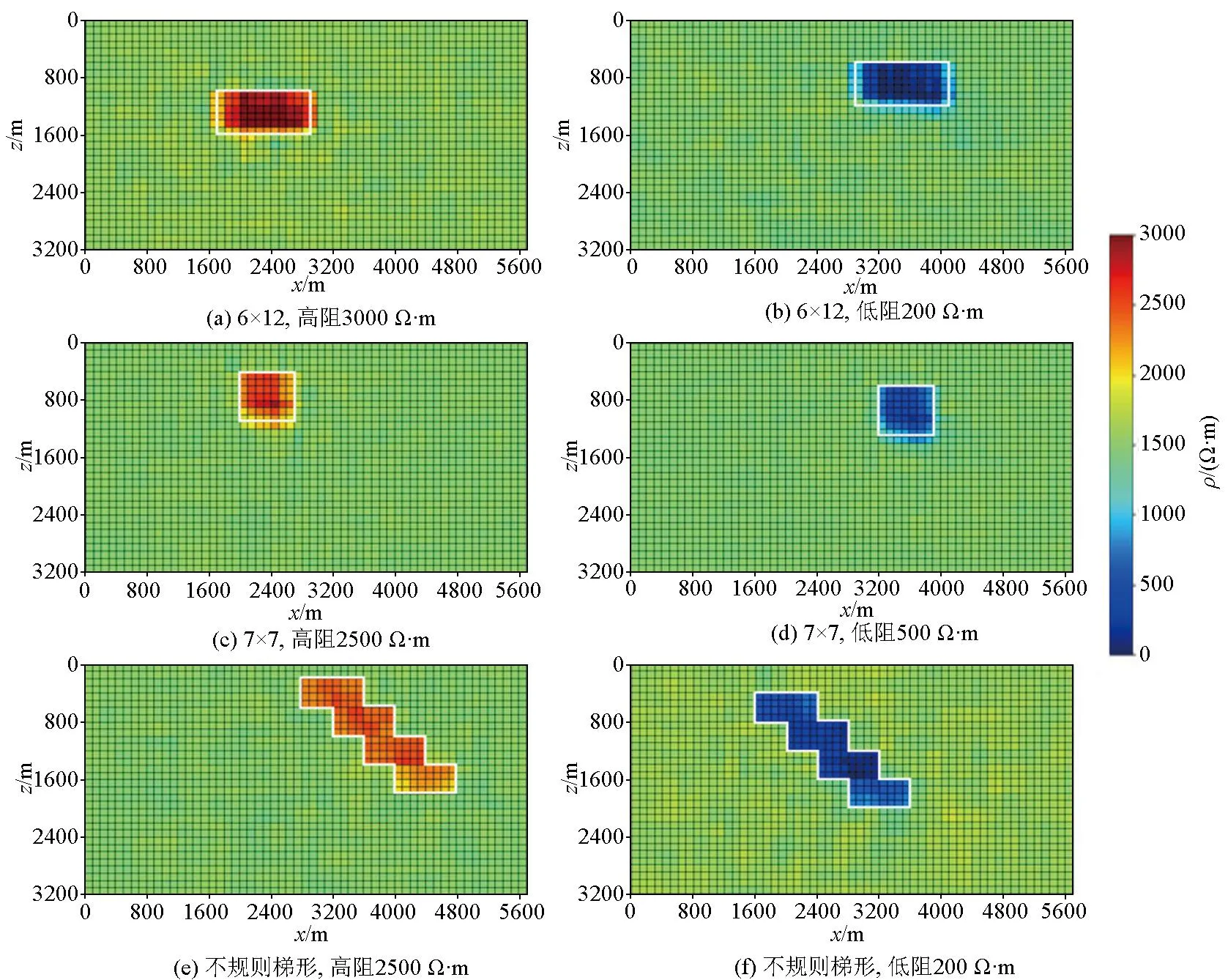
图10 实验一的反演结果
3.5.2 实验二
采用“学习”过的形状(6×6、4×8、3个4×8堆叠的不规则梯形)搭配未“学习”过的电阻率参数(2 800、2 300、700 Ω·m)构成测试集来进行评估。
图11为随机抽取的几组反演结果,可见反演得到的模型位置、形状以及电阻率值均与真实模型基本一致。
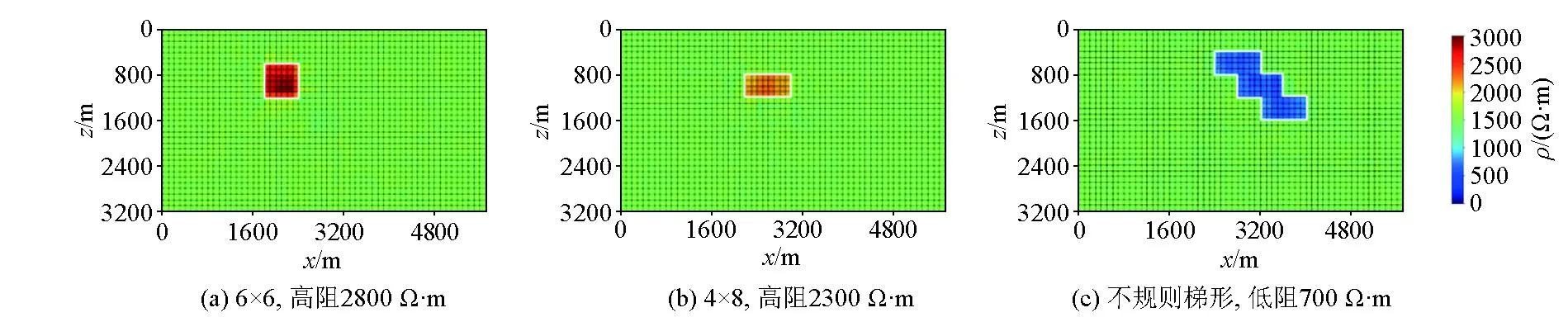
图11 实验二的反演结果
3.5.3 实验三
为了进一步评估本方法的泛化能力,实验三采用未“学习”过的形状(7×7、4个4×8堆叠的不规则梯形)搭配未“学习”过的电阻率参数(2 300、700 Ω·m)构成测试集来进行评估。反演结果(图12)表明, 反演得到的模型位置以及形状与真实模型一致,电阻率数值与真实值接近,仅少许单元格的电阻率值低于实际值。由此说明本文iResNet网络可以用来解决大地电磁反演问题,并且具有较好的泛化能力。
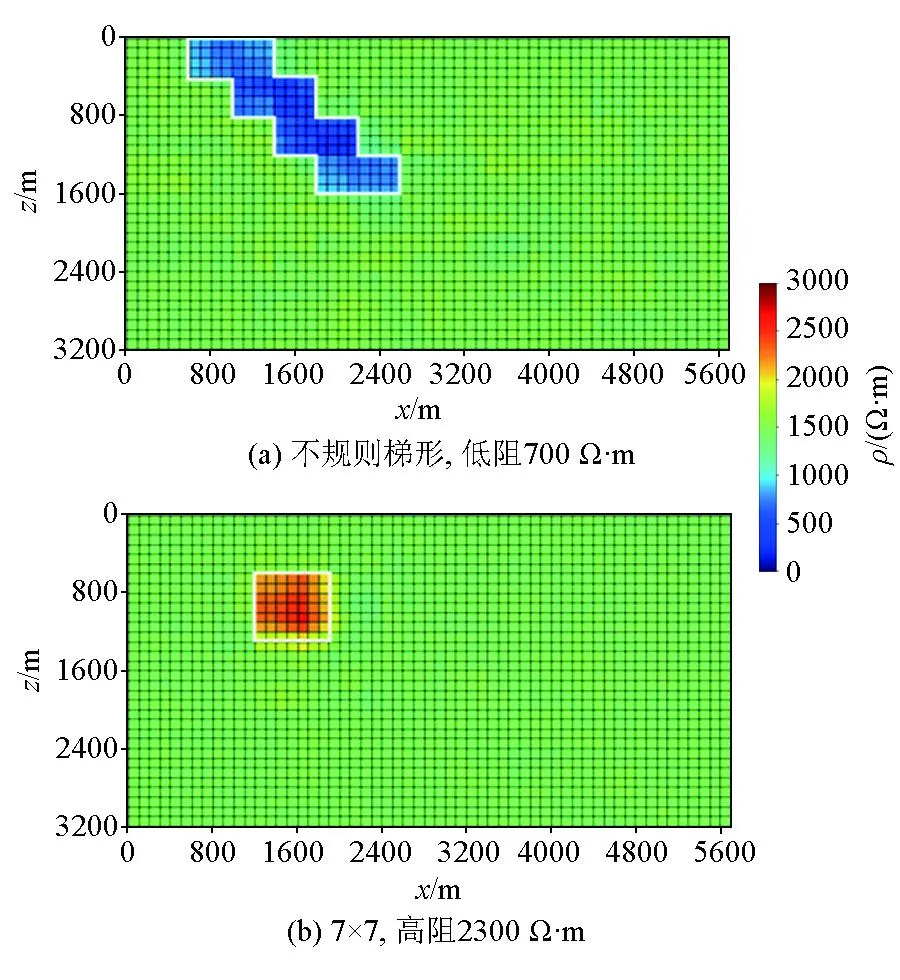
图12 实验三的反演结果
3.6 抗噪能力测试
在真实环境中,大地电磁通常受噪声等因素的影响,因此将高斯白噪声添加到视电阻率数据中,以分析网络的抗噪能力。抗噪能力实验采用前文3.1节中的7种模型,正演时在视电阻率数据中分别加入3%和5%的高斯白噪声(图13),构成数据集用以训练网络,并用实验一中设计的未“学习”过的模型来评估网络的抗噪能力。
由图14、图15可以看出,无论是加入3%还是5%的高斯白噪声,反演结果受噪声的影响均较小,反演得到的模型形状、位置都接近于真实模型,仅模型边缘较少单元格的电阻率值略低于实际值,说明本文所提网络具有较好的抗噪声能力。

图14 加入3%高斯白噪声后的反演结果
4 实例
以非洲南部实测大地电磁数据[12]为例,探讨验证iResNet网络的可行性与反演结果的可靠性。图16所示为非洲南部的刚果克拉通(Congo craton)和达马拉—杭济—乔贝带(Damara—Ghanzi—Chobe Belt)的详细地质图。前人认为在ETO007~ETO009间可能存在达马拉造山带与刚果克拉通南部间的分界线。本文重点研究ETO009及之后的6个测点,即ETO009~ETO014[17]。这6个测点分布于Damara Northern Zone、Damara Northern Margin Zone、Northern Damara basement_Kamanjab Inlier3块区域,前人将这3块区域统称为南部刚果克拉通(Southern Congo craton)的Northern zone[18]。
本文选择以下27个频点进行研究:0.0092、0.0134、0.0183、0.0269、0.037、0.054、0.073、0.107、0.146、0.215、0.293、0.43、0.59、0.86、1.17、1.72、2.34、3.4、4.7、6.9、9.4、13.7、18.8、27.5、40、66、97 Hz。从图17中的视电阻率数值可以看出,研究区域多为高阻。
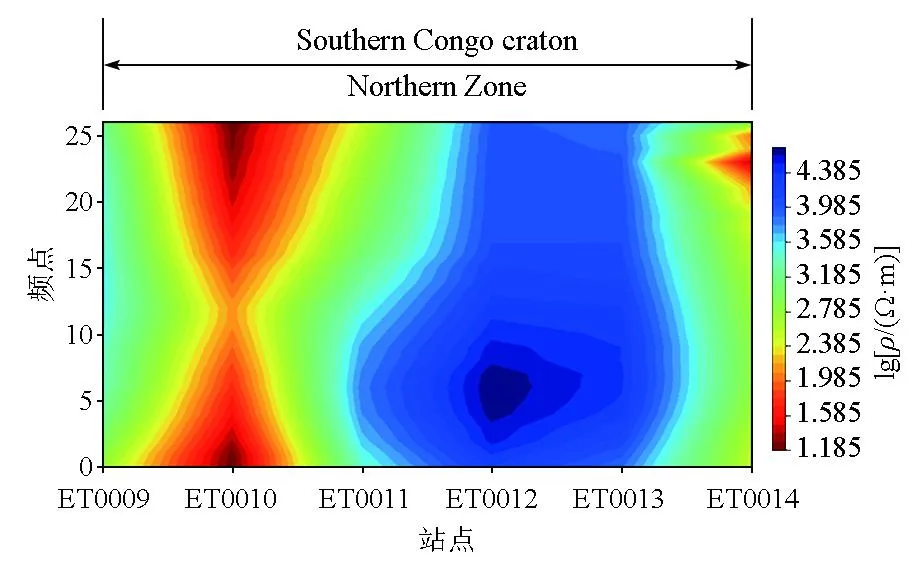
图17 Northern zone的视电阻率
图18为iResNet网络对Northern zone的反演结果,可以看出:该区域整体电阻率值较高,大约为104Ω·m,红色弧线以上的区域电阻率值较低,约为103Ω·m,红色弧线以下区域电阻率值高达104.5Ω·m。现有研究结果表明,Kamanjab Inlier上层为元古代沉积物覆盖层,内层主要为花岗岩和片麻岩,因此呈现出上层电阻率值低,内层电阻率值高(超过104Ω·m)的结果,且在ETO011和ETO012站点之间可以追踪到内层的表面边界[20]。整体而言,本文反演结果与现有研究结果基本一致:iResNet网络可以大体反映出地下物性的分布范围与趋势,并划分电阻率值的变化边界。
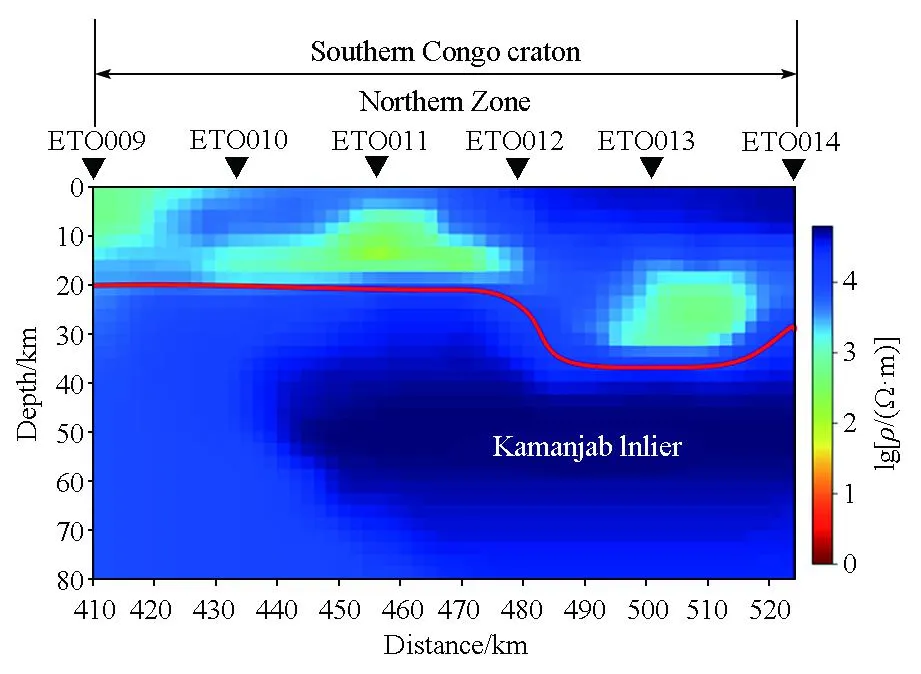
图18 iResNet对Northern zone反演结果
为验证反演结果的准确性,引用Khoza等[18]采用非线性共轭梯度法对非洲南部的KIM+ETO测线进行反演的结果,图19中红色方框即为本文重点研究的区域。通过对比图18与图19,不难看出iResNet反演结果与正则化反演结果相似,但对于电阻率值极低的地质构造,iResNet则无法反演出非常准确的结果。相较于前人使用残差网络对非洲南部大尺度实测数据进行反演的结果[12]而言,本文所使用的iResNet在小尺度上拥有更加精细的反演结果,该反演结果也更加接近正则化反演结果。总体来说,本文方法可以有效用于大地电磁重建地下电阻率结构。
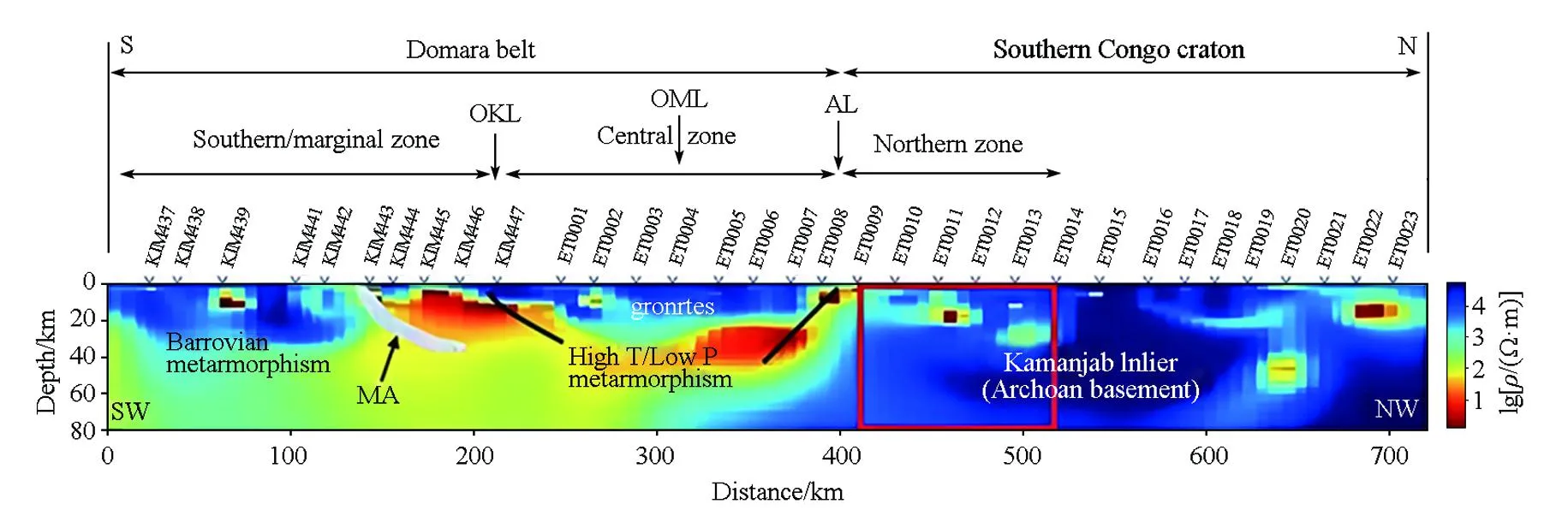
图19 KIM+ETO测线正则化反演结果[18]
5 结论
本文提出一种基于改进残差网络iResNet的大地电磁反演方法。实验结果表明,该方法可以快速准确反演出地电模型的位置、形状和电阻率值,具有较好的泛化能力和抗噪声能力,在实际资料处理中具有一定的实用性,能用于大地电磁二维反演问题。但该方法也存在一定的局限性,例如本文的目标函数中重点约束的是模型形状,由此导致网络会牺牲模型电阻率值的恢复以保证模型形状的恢复,因此在今后的工作中,可以进一步修改目标函数使其能对模型的电阻率值进行约束,从而提高反演的精度。如今,残差网络应用较为广泛,但面对更加复杂的三维反演工作,如何进行网络结构的优化和数据的选取也值得进一步深入研究。

