门式起重机风载稳定性分析
汪敬东 叶炯振 程 玲 秦 昊 刘 华
1 上海市特种设备监督检验技术研究院 上海 200062 2 上海市浦东新区特种设备监督检验所 上海 200062
3 江苏恒浩机电设备安装工程有限公司 泰兴 225400
0 引言
造船门式起重机(简称造船门机)是现代船坞、船舶制造作业的大型特种设备[1]。起重机的设计更倾向于轻量化设计理念,其中薄壁特性常采用板、壳、加筋板壳和组合板壳等轻结构形式,然而,这一特性也将导致造船门机产生局部结构的稳定性下降[2]。
近年来,各界专家学者亦从不同专业角度对造船门式起重机其结构稳定性进行了分析并取得了许多优秀的研究成果。赵晓姣等[3]通过可拓集合的关联函数计算评价指标对失效等级的关联系数,引入层次分析法(Analytic Hierarchy Process,AHP)计算指标权重,根据级别变量特征值判定桥式起重机失效可能性等级,评价其结果与实际情况相符与否,为桥式起重机安全评价提供了一种有效的新途径;袁楷等[4]针对起重机的检验方式提出了应用视频监控、物料识别等方式填补了智能网联在安全技术规范应用的空白;戚其松等[5]提出了基于神经网络对起重机服役期间的载荷谱进行分析,并预测了起重机关键部位寿命。然而,针对造船门机其结构迎风面积大这一特性,考虑风载荷对其结构强度、刚度以及稳定性影响的理论研究仍然较少。加筋板作为造船门机重要典型的承载结构,在造船门机主梁以及刚柔腿中大量运用,也是箱形梁类型起重机的共有特征。其在承载条件下的稳定性直接影响到起重机的承载能力,也关乎整机的安全运行。本文基于造船门机加筋板实际结构,建立了加筋板动力学响应模型,分析加筋板结构在风载荷作用下稳定性相关影响因素及其影响规律,为造船门式起重机稳定性的安全评估提供理论基础。
1 加筋板动力学响应方程
针对起重机加筋板承受风载荷特征,建立相应如图1 所示典型加筋板结构,坐标原点取在板的中面上,共有i根纵筋、j根横筋。板四边简支,受横向均布载荷q(t)作用。其中筋板高度为h1、厚度t1,面板厚度为hp,xi为第i根y向加筋的中线坐标,yj为第j根x向加筋的中线坐标。
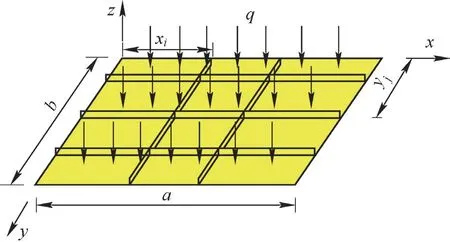
图1 加筋板结构示意图
1.1 面板基本方程
由薄板的大挠度理论,面板中面应变位移满足
式中:m为中面应变,u、v、w为面板中面位移。
由于u和v相对于w小很多,故这里忽略板中面位移u和v。设板截面的应变在板厚度方向线性变化,则对于板有
由广义胡克定律可以得到面板的应力为
在厚度方向对应力进行积分,可以得到面板单位宽度上的内力Nx、Ny、Nxy及内力矩Mx、My、Mxy
在大挠度理论中板的中面薄膜力是不能忽略的,为此引入应力函数φ,则有
由式(3)和式(4)可得板中面的应变和内力之间的关系
将式(5)带入得
板的挠曲线曲率为
1.2 加筋基本方程
对于加强筋,假设在接触处加强筋与面板的变形相同,则对于第i根横筋和第j根纵筋有
由上式可得到加强筋中面应变为
假定加强筋与面板的材质相同,则可以得到
式中:I和J分别为筋对面板中面的惯性矩和扭转惯性矩。
1.3 加筋板控制方程
将加筋板看作板和筋的组合结构,则对于加筋板系统,Hamilton 变分原理表达式为
式中:T、U、W分别为系统的总动能、应变能和外力功,符号δ为一阶变分符号。
1.3.1 加筋板系统的总应变能
加筋板系统的总应变能可表示为
式中:Up为板的应变能,Uxi、Uyj分别为加筋的应变能,δxi和δyj为delta 函数。
1.3.2 加筋板系统的总动能
加筋板系统的总动能可表示为
式中:Tp为板的动能,Txi、Tyj分别为加筋的动能。
1.3.3 加筋板系统的总外力功
设加筋板受到横向载荷为q(t),则外力做功为
将式(13)、式(15)和式(17)带入式(12)后整理可得加筋板的控制方程为
又有板的变形协调方程为
四边经典简支的加筋矩形板的位移应满足
设位移函数w和应力函数的试函数φ分别为
式中:m、n分别表示x、y方向的半波数。
显然满足所有边界条件。
将式(21)和式(22)带入式(18)和式(19),可得wmn(t)和φmn(t)关于变量x、y和t的微分方程。所以这里先采用加权残值法中的伽辽金法对空间变量进行离散,得到关于时间的常微分方程组,最后运用龙格库塔法即可求解。
2 加筋板风载响应工况
面板长度a=1 200 mm,宽度b=600 mm,厚度hp=30 mm。假设面板和加强筋的材料参数相同,弹性模量E=210 GPa,泊松比μ=0.3,密度ρ=7.8 g/mm3,纵向和横向加强筋尺寸相同:厚度t1=5 mm,高度h1=20 mm,纵向和横向均只布置一根筋,且位于面板中间位置。
本文主要研究动载荷扰动强度q0、扰动时间td、面板厚度hp及筋板高度h1对加筋板动载响应的影响,因此设计如下计算方案,在讨论其中某参数的影响时,保持其他参数不变。
1)保持加筋板相关几何尺寸不变,令改变动载荷强度,分别取q0=1 MPa、6 MPa 及10 MPa;
2)保持加筋板相关几何尺寸不变,改变动载荷加载时间,分别取td=10 μs、20 μs 及30 μs;
3)改变加筋板厚度值,分别取hp=0.01 m、0.03 m 及0.04 m,保持加筋板相关几何尺寸以及扰动载荷不变;
4)改变加筋板高度值,分别取h1=0.01 m、0.02 m 及0.03 m,保持加筋板相关几何尺寸以及扰动载荷不变。
3 加筋板风载响应结果分析
1)载荷强度对加筋板动载响应的影响
图2 为不同载荷强度下加筋板挠度响应规律。从图中可以看出,加筋板挠度响应曲线规律类似,扰动初期产生与扰动曲线类似阶跃,再经历相对稳定阶段,最终振荡趋于平衡位置。同时随着载荷强度增大,振幅最大值呈现递增趋势,从2.1 mm 增大至18.1 mm,增大趋势显著。

图2 不同载荷强度下加筋矩形板挠度响应曲线
2)动载时间对加筋板动载响应的影响
图3 为不同扰动时间下加筋板挠度响应规律。从图中可以看出,加筋板挠度响应规律类似,随着扰动时间的增大,响应时间也相应延长,振幅变化不大。

图3 不同加载时间td 下加筋矩形板挠度响应曲线
3)板厚对加筋板动载响应的影响
图4 为不同板厚条件下加筋板动载响应规律。从图中可以看出,加筋板挠度响应曲线规律类似。随着面板厚度增大,振幅呈现递减趋势,从28.2 mm 减小至6.3 mm,减小趋势明显。说明随着加筋板厚度增大,筋板响应幅度显著减小。

图4 不同面板厚hp 下加筋矩形板挠度响应曲线
4)筋板高度对加筋板动载响应的影响
图5 为不同筋板高度条件下加筋板挠度响应规律。从图中可以看出,加筋板挠度响应曲线规律类似。随着筋板高度增大,振幅呈现递减趋势,从16.8 mm 减小至6.1 mm,削弱趋势明显。说明随着加筋板高度增大,筋板响应幅度显著减小。

图5 不同筋板高度h1 下加筋矩形板挠度响应曲线
4 加筋板冲击动力学稳定性分析
4.1 加筋板动载临界载荷理论推导
将式(21)和式(22)带入式(18)和式(19),可得wmn(t)和φmn(t)关于变量x、y和t的微分方程。先采用加权残值法中的伽辽金法对空间变量进行离散,得到关于时间的常微分方程组,然后运用龙格库塔法即可求得位移函数参数wmn(t),后取其最大值作为加筋板最大位移响应值,因此可得不同冲击强度q0作用下加筋板的最大位移响应值wmax,然后运用B-R 准则来确定临界载荷,如果所加的冲击载荷的微小增量可以引起结构的剧烈响应,则所对应的载荷便是结构的临界屈曲载荷。
4.2 加筋板冲击动力学稳定性分析工况
面板几何尺寸与风载响应工况面板一致。本文主要研究面板长宽比k、面板厚度hp、筋板高度h1及厚度t1对临界载荷的影响,因此,设计如下计算方案,在讨论其中某参数的影响时,保持其他参数不变。
1)保持面板宽度b=600 mm 不变,令长宽比k=a/b,则可得不同长宽比k下的B-R 曲线;
2)仅改变面板厚度hp,可得不同面板厚度hp下的B-R 曲线;
3)仅改变筋板高度h1,可得不同加筋高度h1下的B-R 曲线;
4) 仅改变筋板厚度t1,可得不同加筋厚度t1下的B-R 曲线。
5 加筋板冲击动力学稳定性分析结果
1)通过改变加筋板长度几何尺寸,以获取不同长宽比k值,分别取值1.0、1.2、1.4、1.6、1.8、2.0,同时保持加筋板其他几何尺寸以及动载荷不变,获取加筋板加载过程中载荷与最大位移响应值对应的B-R 曲线。从曲线规律图6 中可以看出,长宽比k越大,加筋板模型越呈现狭长状态;长宽比增大,在面内动载荷作用下,加筋板位移响应在相同载荷点位置对应的最大变形值越大,同时递增的趋势也越大,整体B-R 曲线斜率也随之增大,说明加筋板越接近临界失稳状态,相应也表明所对应的模型其承载能力越弱。长宽比越大加筋板动载稳定性越弱。

图6 加筋板不同长宽比k 下加筋矩形板B-R 曲线
2)通过改变面板厚度尺寸值hp,分别取值0.01 m、0.02 m、0.03 m、0.04 m、0.05 m、0.06 m,同时保持加筋板其他几何尺寸以及动载荷不变,获取加筋板加载过程中载荷与最大位移响应值对应的B-R 曲线。从曲线规律图7 中可以看出,随加筋板厚度增大,在面内动载荷作用下,加筋板位移响应在相同载荷点位置对应的最大变形值越小,但总的减小趋势也在削弱,说明影响程度逐步减弱。整体B-R 曲线斜率也随之减小,说明加筋板越远离临界失稳状态,相应也表明所对应的模型其承载能力越强。加筋板厚度越大,其动载稳定性越强。但当达到一定程度,增强效应逐步减弱。

图7 加筋板不同面板厚hp 下加筋矩形板B-R 曲线
3)通过改变筋板高度尺寸值h1,分别取值0.017 m、0.018 m、0.019 m、0.02 m、0.021 m、0.022 m,同时保持加筋板其他几何尺寸以及动载荷不变,获取加筋板加载过程中载荷与最大位移响应值对应的B-R 曲线。从曲线规律图8 中可以看出,随筋板高度增加,在面内动载荷作用下,加筋板位移响应在相同载荷点位置对应的最大变形值越小,同时总的减小趋势在削弱,说明影响程度在逐步减弱,整体B-R 曲线斜率也随之减小,说明加筋板越远离临界失稳状态,相应也表明所对应的模型其承载能力越强。加筋板高度越大,其动载稳定性越强。但当达到一定程度,增强效应逐步减弱。

图8 加筋板不同加筋高度h1 下加筋矩形板B-R 曲线
4)通过改变筋板厚度尺寸值t1,分别取值0.02 m、0.03 m、0.04 m、0.05 m、0.06 m、0.07 m,同时保持加筋板其他几何尺寸以及动载荷不变,获取加筋板加载过程中载荷与最大位移响应值对应的B-R 曲线。从曲线规律图9 中可以看出,随筋板厚度增加,在面内动载荷作用下,加筋板位移响应在相同载荷点位置对应的最大变形值越小,同时总的减小趋势在削弱,说明影响程度在逐步减弱,整体B-R 曲线斜率也随之减小,说明加筋板越远离临界失稳状态,相应也表明所对应的模型其承载能力越强。加筋板厚度越大,其动载稳定性越强。但当达到一定程度,增强效应逐步减弱。

图9 加筋板不同加筋厚度t1 下加筋矩形板B-R 曲线
6 结论
本文基于起重机承受风场动载荷这一特征,建立了加筋板动力学响应模型,并通过理论计算得到了如下结论。
1)随着载荷强度增大,加筋板响应幅度增大明显,且各载荷强度工况下,加筋板挠度响应曲线规律类似,扰动初期产生与扰动曲线类似阶跃,再经历相对稳定阶段,最终振荡趋于平衡。
2)随着扰动时间增长,响应时间也相应延长,振幅变化不大。
3)随着加筋板厚度和高度增大,筋板响应幅度显著减小,且在各工况下,加筋板挠度响应曲线规律基本相似。
4)面板长宽比越大,加筋板动载稳定性越弱:加筋板厚度、筋板高度与筋板厚度越大,其动载稳定性越强,但当达到一定程度,增强效应都会逐步减弱。

