溶蚀白云岩含水层注浆浆水两相运移特征LBM模拟研究

周禹良 袁东锋 杨 雪 李 斌

(1.华北科技学院安全工程学院,河北 廊坊 065201;2.北京中煤矿山工程有限公司,北京 100013;3.矿山深井建设技术国家工程研究中心,北京 100013)

矿井水害具有强烈的致灾性,若发生涌水量过大或突水淹井事故,将造成巨大的经济损失和恶劣的社会影响[1-2]。注浆技术是一种主动防治矿井水害的有效手段[3-4],是通过一定压力将浆液注入地下含水层,驱排地层中的地下水,浆液凝固后充填封堵地层导水通道形成注浆帷幕[5-6],提高岩体的黏聚力和内摩擦角[7-8],以达到堵水和加固地层的目的。岩体注浆是典型的多相流问题[5-9],涉及的流体主要是浆液和地下水。通常,浆液黏度和密度均大于地下水,且不同类型浆液和地下水之间存在不同程度的混溶现象,造成浆液和地下水之间的相互作用复杂。注浆过程中,浆液在注浆压力驱动下排出导水通道中的地下水,除了浆液本身运移产生的摩擦外,地下水流动也将产生一定压力损失。如图1所示,采用常规单相流模型将导致浆液扩散范围分析存在偏差。同时,传统单相流注浆分析方法忽略浆-水相互作用,难以考虑浆液和地下水的物性差异。

图1 传统单相流模型浆液扩散范围偏差Fig.1 Deviation of grout diffusion range predicted by traditional single-phase flow model

为了解决上述问题,Zou等[9]建立了单裂隙中浆-水驱替模型,得到了相界面压力与扩散距离的计算公式。Ozdemir等[10]采用向量体积法研究了孔隙介质中化学浆注浆过程的两相扩散规律。刘人太等[11-12]通过室内试验和数值模拟研究了不同条件下浆-水两相在裂隙中的扩散规律。杨志全等[13]基于Comsol Multiphysics 达西渗流模块研究了幂律型浆液在砾石土多孔介质中的两相扩散规律。研究表明岩体中浆-水两相具有明显的非均匀扩散特征,浆-水之间的黏度差和复杂的导水通道网络易诱发浆液扩散产生指进现象,降低注浆驱水效率。近年来,随着CO2地质封存,非常规油气资源采收和地热开采等项目的实施,复杂地层中多相流研究得到极大的关注。JU等[14-15]采用格子玻尔兹曼方法(LBM)模拟了岩体介质非均匀孔隙系统内的非混相水油驱替过程。Zakirov等[16]研究了不同润湿条件和毛细管压力下孔隙的各向异性对两相驱替行为的影响。由于LBM方法具有适合处理岩土多孔介质复杂边界和易于并行的优点,基于数字岩芯的LBM模拟技术在岩体多相流及流固耦合方向具有良好的应用前景。

综上分析,现有注浆模型虽然考虑了浆液黏度时变性、裂隙开度、注浆压力等因素对浆液扩散范围的影响,但对浆液驱替地下水效应考虑不充分,难以处理复杂导水通道网络中的浆-水相互作用,造成浆液有效扩散范围分析结果偏大。浆-水两相扩散范围决定注浆帷幕交圈厚度和注浆帷幕堵水有效性,关系注浆堵水的成败。目前,深部开采矿井水害防治问题越来越突出[17-18],浆-水两相驱替运移规律是注浆堵水技术极为重要的基础问题。因此,开展岩体注浆浆水两相驱替机制和运移规律研究具有重大理论意义和工程价值。本文采用图像处理方法识别溶蚀白云岩岩芯导水通道,利用三维重构技术获得导水通道三维数字模型。然后,基于Shan-Chen模型描述浆水两相相互作用,采用LBM模拟岩体注浆过程中浆水两相驱替行为,分析了浆相饱和度和残余地下水的演化特征,揭示浆水驱替机制,为注浆防治矿井水害提供技术参考。

1 LBM基本原理及浆-水相互作用模型

1.1 LBM模型及原理

格子玻尔兹曼方法采用离散格式求解连续Boltzmann方程,是一种计算流体力学方法。该方法能够适应复杂边界条件,同时具有程序实施相对简单和易于并行等优点[19]。如图2所示,以二维格子模型D2Q9为例来介绍LBM的原理。空间流域离散为格子,时间离散为固定的时间步长。格子通过离散的节点联系,节点包含粒子,粒子在节点内运移并和相邻节点产生接触,实现动量和能量的交换。LBM并不追踪单个分子,而是一群粒子,也即通过概率密度函数来代表粒子的运动。在节点上,流体的宏观物理力学参数如密度和速度取决于分布函数和粒子迁移方向,计算公式为

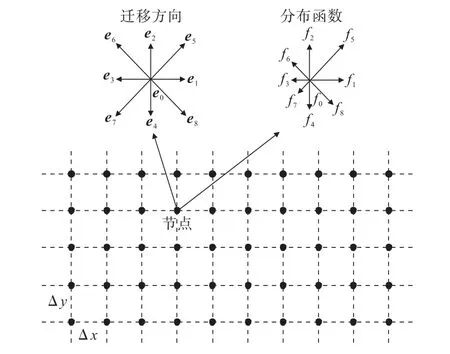
图2 D2Q9格子节点和迁移方向示意Fig.2 Sketch map of D2Q9 lattice and streaming direction of the particles

式中,ρ为格子节点上流体密度;fi为第i迁移方向上的分布函数;u为格子节点上流体速度;ei为第i迁移方向的向量。

格子中粒子分布函数的迁移和碰撞过程如图3所示,粒子分布函数演化方程表示为

图3 D2Q9格子和分布函数碰撞迁移过程示意Fig.3 Sketch map of D2Q9 lattice and collide-streaming of the particles

式中,x为节点位置矢量;t为时间;Δt为时间步长;τ为松弛因子;feqi为平衡态分布函数。

LBM碰撞过程可以看作是分布函数向平衡状态的松弛。D2Q9模型中,平衡状态的分布函数feiq定义为

式中,c为基本格子速度,取1 lu·t/s;wi为第i迁移方向的权重,当i=0时,w0取4/9;当i=1,2,3,4时,wi取1/9;当i=5,6,7,8时,wi取1/36。

根据绝热状态方程,流体压力取决于密度,计算公式为

式中,cs为格子声速,cs=

采用D2Q9格子模型,流体的运动粘度为

当τ＞0.5时,代表实际物理粘度为正值。当τ→0.5时,会造成数值计算不稳定。

1.2 浆水相互作用模型

Shan-Chen多组分模型是当前最常用的多相LBM模型之一,该模型通过引入伪势来表征多相粒子间的相互作用。格子中,浆水两相分别通过自身的粒子分布函数表示,当空间格子离散格式为DnQb时,组分k的分布函数演化方程为

式中,下标k代表流体组分,k=g、w,分别表示浆液和地下水;i为离散速度个数,i=0,1,2,…,b-1;fki(x,t)为t时刻、位置x上组分k的粒子分布函数;为组分k的平衡态分布函数;τk为组分k的松弛时间,取决于流体的运动黏度,由υk=c2ks(τk-0.5)确定。

流体组分k的密度和速度采用对应的分布函数计算,公式为

流体组分k的平衡态粒子分布函数为

式中,为组分k的平衡态速度。为了模拟浆水的相互作用,假设浆液和地下水两相粒子之间存在相互作用势,相应的势函数[19]为

式中,x'=x+ciΔt为与当前节点紧临的格子节点位置;(x,x')满足(x,x')=(x',x),决定了流体组分k和之间的相互作用强度;ψk是流体组分k局部密度的函数,表示组分k的有效密度。

一般地,函数(x,x')只考虑最临近格点的相互作用。

式中,δ为格子间距;参数绝对值的大小表征组分k和的粒子间的相互作用的强弱,的符号决定粒子间相互作用是相互吸引还是排斥,负值是相互吸引而正值则为相互排斥。构成一个对称的相互作用矩阵。当对角元素都为负值,而非对角元素都为正值时,同组份相互吸引而异组分相互排斥。

根据相互作用势原理,组分k的粒子在x处受到的长程作用力与x处和x'处的有效密度的乘积成正比,计算公式为

粒子间相互作用力Fk对分布函数的影响是通过对组分k的平衡态速度ueqk的影响来体现的。

式中,u(x)是混合流体宏观速度,其计算公式为

为了保证流体系统的动量守恒,平衡态速度进行了重新定义为

两相流体的分离通过选取足够强G的和函数ψ(ρ)实现。Shan和Chen等建议采用指数形式的有效密度函数

式中,ρk0是组分k的参考密度。

2 溶蚀白云岩导水通道识别及三维数字模型

2.1 导水通道三维数字模型重构流程

为了获得溶蚀白云岩复杂导水通道的三维结构,采用X射线微纳米CT扫描、图像处理技术和三维重构技术构建岩样导水通道三维数字模型,为浆水两相运移规律数值模拟提供流场的几何文件。如图4所示,首先,采用X射线微纳米CT扫描技术获得岩样高分辨率CT扫描图片;然后,通过图像处理技术并运用阈值分割识别岩样CT扫描图片中的导水孔隙和裂隙,将图片像素分为固体基质、接触边界和流体区域;最后,依据处理好的CT扫描图像,采用Matlab代码逐层重构岩石导水通道三维数字模型,为岩样中浆水两相运移特征LBM模拟提供几何文件。

图4 岩石导水通道三维重构示意Fig.4 Sketch map of 3D reconstruction of water conducting channels in rock

2.2 溶蚀白云岩试样微纳米CT扫描源文件

溶蚀白云岩作为特殊的多孔介质,其赋水特征和渗透特性与常规裂隙岩体不同。对于溶蚀孔隙型岩体,小孔、微孔是地下水赋存的主要存储空间,而中等及以上溶孔构成的孔隙网络是地下流体运移的主要通道。本文采用的溶蚀白云岩岩样的微纳米CT扫描源文件包含288张CT扫描切片,分辨率为250 μm。x、y、z方向上像素分别为791、791、100。溶蚀白云岩岩样孔隙切片及孔隙率分布情况如图5所示。

图5 溶蚀白云岩切片及孔隙率分布Fig.5 Slice of the dissolved dolomite sample and its porosity distribution

2.3 白云岩试样导水通道三维数字模型

(1)图像处理与导水通道识别。为了识别试样导水通道,首先将图片进行滤波去噪处理,然后利用图片处理软件ImageJ通过阈值分割法来识别岩样中的孔隙结构。如图6(a)所示,通过选择合适的阈值,准确识别切片中的孔隙,然后将图片二值化,得到图6(b)所示的二值化切片图,除边界轮廓外,图片中白色区域部分为孔隙空间,灰度值为255,边界轮廓内部的黑色区域为岩石基质,灰度值为0。将二值化的CT扫描切片图像重叠,就可得到溶蚀白云岩岩样的三维孔隙网络结构,如图6(c)所示。

图6 孔灰度图片阈值分割与二值化Fig.6 Threshold segmentation and binarization of the grayscale image

(2)导水通道数字模型三维重构。由于配备的工作站处理能力有限,选择岩芯局部区域进行孔隙岩样三维数字模型三维重构。如图7(a)所示,选择的研究区域宽150像素,高100像素,切片张数为100张。由于后续模拟软件中的流动方向为x方向,也即垂直切片的纵向方向。因此,在三维重构中,设置图片宽度方向为y方向,图片高度方向为z方向。孔隙岩样数字模型三维重构程序采用Matlab代码,如果某一体素为流体区域,则标记为0;固体基质体素则标记为2,而固体和流体的接触层体素标记为1,获得三维孔隙网络数字模型如图7(b)所示。

图7 溶蚀白云岩岩样三维数字模型Fig.7 Three-dimensional digital model of dissolved dolomite rock sample

3 溶蚀白云岩注浆浆-水两相运移特征

3.1 模拟软件简介

溶蚀白云岩注浆过程中浆水两相运移特征采用Palabos软件进行模拟分析,模拟运算采用Linux计算工作站,配置Xeon(R)Gold 6230 双CPU,40核心,128G内存。Palabos是以LBM为内核的通用CFD开源分析软件,该软件编程接口界面采用C++编写,内置了单相流、多相流以及多场耦合模型,同时包含多种碰撞格式的类可供用户调用,具有处理复杂边界条件和并行计算效率高等优点。由于该软件没有图形界面,采用第三方软件ParaView进行模拟结果的三维可视化分析。

3.2 初始和边界条件及浆-水两相基本参数

模拟分析的几何文件采用前述溶蚀白云岩岩样三维数字模型,每一个体素为一个格子单元,格子迁移速度模型采用D3Q19模型,如图8(a)所示。浆-水两相初始条件及边界如图8(b)所示。模拟流动方向为x方向,左侧为流体入口,右侧为流体出口,模型四壁和内部岩石基质格子为反弹边界条件,也即无滑移边界条件。模拟中,采用Shan-Chen模型描述浆-水两相间相互作用,浆水两相基本物理力学参数列于表1。

表1 岩体注浆模拟中浆-水物理力学参数Table 1 Pysical and mechanic perameters of the grout amd water

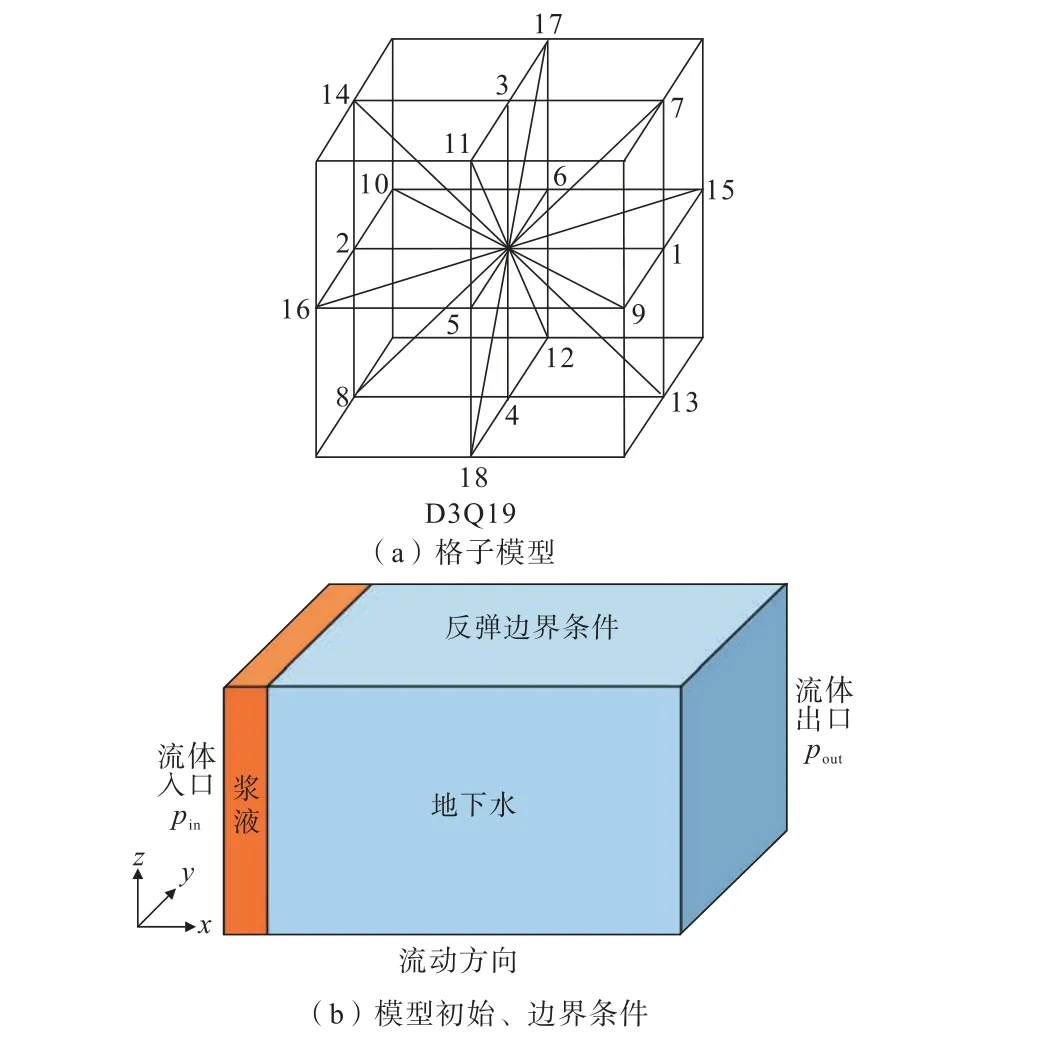
图8 浆-水两相运移模拟的格子模型以及初始和边界条件Fig.8 Lattice model and initial & boundary conditions for simulation of grout water two-phase transport

3.3 模拟结果分析

(1)孔隙岩样渗透率分析。采用溶蚀白云岩岩样的三维数字模型可进行岩样绝对渗透率分析。渗透率是表征岩土介质传输流体能力的关键参数。岩样绝对渗透率与孔隙度、孔隙几何形状、迂曲情况、岩土颗粒大小及排列方式等因素有关。图9为白云岩岩样孔隙连通情况和渗透率模拟结果。从图9(a)可以看出,白云岩试样孔隙发育,孔隙大小和形状分布复杂,通过软件统计分析得到研究区域的平均孔隙率为0.42,但在x方向上孔隙连通程度相对较差,存在较多的孤立孔隙区域。图9(b)为试样中模拟的流动速度分布情况,可以看出,流体选择沿连通性较好的大孔隙运移,同时,孔隙中部流速明显大于孔隙壁面附近流速,孔隙壁面摩擦对流体流动产生明显的抑制。试样的真实物理渗透率是格子渗透率乘以空间分辨率的平方。模拟得到的格子单位渗透率为kl=0.095 8 lu2,空间分辨率为23 μm/像素,换算后可以得到研究区域的真实绝对渗透率为kp= 50.70 μm2,属高渗透率岩样。

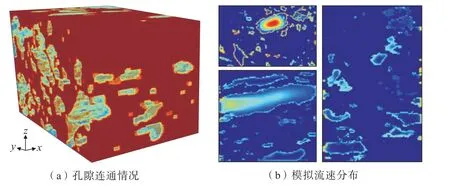
图9 Guelph 白云岩岩样渗透率模拟结果Fig.9 Simulated permeability of Guelph dolomite rock sample

(2)孔隙岩样中浆水两相运移特征。设浆相到达出口的时间点为t0,如图10所示,选择4个不同的相对时刻来分析浆水两相运移分布情况。在注浆压力作用下,浆液开始驱替地下水。初始阶段,入口处孔隙结构和孔径大小对浆相运移具有重要影响。浆液易沿大孔中部向前推进,形成平缓的相界面。由于孔径网络连通情况的不同,浆相前沿推进距离不同。小孔和连通性较差的孔隙中,浆相前沿明显滞后。驱替初始阶段,孔隙壁面附近残存一定地下水,随着注浆时间的增加,孔隙壁面附近地下水逐步减少。浆液驱替地下水行为具有明显的非均质性(各向异性),浆液扩散具有明显的选择性,连通性较好的孔隙为浆相主要运移通道,浆相最先达到出口。由于浆液不能完全排出孔隙壁面附近地下水,同时,后续浆液固结过程中可能会析出少量地下水,造成浆液固结体与孔隙壁面不能有效接触,是注浆堵水的薄弱环节。孔隙岩样中孤立孔隙中的地下水几乎不能被浆液驱替。被束缚的地下水降低了整个孔隙岩样的渗透性,后续浆液沿着已经驱替形成的优势通道运移扩散,降低了注浆驱水效率。

图10 Guelph 白云岩岩样中浆-水两相驱替行为模拟结果Fig.10 Displacement behavior of grout and water in Guelph dolomite rock sample

4 结 论

(1)溶蚀白云岩试样轴向方向上孔隙连通程度相对较差,存在较多的孤立孔隙区域,试样平均孔隙率为0.42。注浆过程中,浆液选择沿连通性较好的大孔隙运移,孔隙中部流速明显大于孔隙壁面附近流速,孔隙壁面摩擦对流体流动产生明显的抑制。

(2)驱替初始阶段,孔隙壁面附近残存一定地下水,随着注浆时间的增加,孔隙壁面附近地下水逐步减少。浆液驱替地下水行为具有明显的非均质性,浆液扩散具有明显的选择性,连通性较好的孔隙为浆相主要运移通道,浆相最先达到出口,孤立孔隙区域中的地下水基本不能被浆液排出置换。

(3)被束缚的地下水降低了整个孔隙岩样的渗透性,后续浆液沿着已经驱替形成的优势通道运移扩散,降低了注浆驱水效率。单次注浆浆液很难完全排出孔隙壁面附近地下水,而且浆液固结过程中也会析出少量地下水,造成浆液固结体与孔隙壁面之间很难有效接触,是注浆堵水的薄弱部位。