基于海底基准的中远程PNT定位导航技术及验证

郑翠娥, 程驰宇, 韩云峰, 张居成

(1.哈尔滨工程大学 水声技术全国重点实验室, 黑龙江 哈尔滨 150001; 2.海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001; 3.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001)

水下定位导航授时体系(positioning, navigation and timing,PNT)建设是世界海洋强国必争的高技术战略领域,美国、加拿大、欧盟等早已开启了相关研究,日本已在其近海建立了海洋PNT基准网,而我国水下PNT建设规模小、功能单一、布设原则不能满足大区域水下PNT 基准网、建立的海洋声速场精度和分辨率难以满足高精度水下PNT 基准网建设及服务要求[1-5]。随着我国海洋强国战略的快速推进和核心技术的迅猛发展,对水下PNT基础设施建设的需求愈发迫切。“十三五”期间,杨元喜院士主持开展“海洋大地测量基准与海洋导航新技术”,在南海建设示范区,主要应用于海底精密工程测量、海底形变监测,UUV水下导航等,实现了米级精度的水下声学导航[6]。“十四五”期间,“问海”计划构建水下PNTC网络,为建设透明海洋提供支撑。水下PNT基础设施建设的迫切性不仅是由于美俄等世界强国在水下作战需求的牵引,更是将“北斗”等导航系统时空基准向海洋与水下延伸,以构建海洋水下导航系统[7]。海底基准是水下PNT的关键基础设施,基于海底基准的水声定位导航技术是海洋水下导航的关键技术,为构建水下综合PNT体系提供技术支撑[8-9]。

为实现水下综合PNT基础设施的广域性建设,满足水下用户的广域性需求,需要海底基准支持更远距离的定位导航[10]。工作频率限制了海底基准的作用距离,目前深海声学高精度定位导航常采用工作频率为10 kHz频段的海底基准,海底基准在深度3 000 m、距离目标11 km实现了优于10 m的定位导航精度[11]。为实现中远程20 km量级以上的作用距离需要采用更低工作频率(如3 kHz频段)的海底基准,然而其定位导航性能随工作频率的下降而下降。

在中远程条件下,声线翻转修正困难引起的声速获取不准和长传播延时引起的静态模型近似误差是影响定位导航精度的主要问题。

声速在海水中呈垂直梯度分布,主要随深度方向变化,声波在水下沿弯曲路径传播,在中远程传播过程中发生声线翻转[12]。水下定位导航模型通过时延与常声速的乘积获取距离观测量,而声线弯曲和翻转会引入声速相关误差,使得导航定位误差增大[13]。对于声速相关误差的消除,一般考虑结合实测声速剖面,通过时延测量信息准确修正距离测量信息,基于射线声学理论实现声传播路径的准确跟踪。现有水下定位的声线跟踪方法不完善,多以中近程非翻转声线跟踪为主,基于声速剖面近似等梯度分层的思想,迭代求解有效声速和目标位置[14]。在此基础上,发展了考虑波束入射角的常梯度声线跟踪水下定位算法,实现了声线入射角先验未知情况下的有效声速和目标坐标的渐次修正,考虑目标与海底基准的声线入射角度过大时,传统声线跟踪方法对入射角的迭代解算会出现发散问题,研究了大入射角声线跟踪方法,实现了不小于80°入射角声线的稳健跟踪[15-16]。然而,对于中远程翻转声线跟踪难题尚未存在有效解决措施。

由于声波在海洋中传播速度慢,运动目标接收来自各海底基准所发射定位声信号的时刻、位置均不同。在深海、中远程的长传播延时条件下,产生了不可忽略的静态定位模型近似误差。在传统静态定位模型的基础上,利用目标运动速度补偿静态模型近似误差的运动目标长基线定位解算方法得到广泛应用,在缺少目标外测速度信息情况下,基于测时修正量的动态补偿方法(motion-compensated model,MM)仅利用声学测时数据消除了模型近似误差,实现了运动目标的高精度定位[17-18]。

本文基于中远程声学PNT基准系统,首先介绍了海底基准定位导航原理,并分析了深海中远程定位的特点和难点,基于此,本文提出了一种中远程声学定位导航方法,结合南海3 000 m深水域实测水下用户导航数据,得到了深海中远程海底基准的定位导航性能。

1 海底基准声学定位导航原理及分析

1.1 声学定位导航基本原理

水下目标在深海场景下的位置高精度获取方式一般采取在海底布设不少于3个声学基准,通过各海底基准与目标之间的测距信息交汇解算目标坐标[19]。由于海深尺度限制、声速在垂直方向不均匀等因素的存在,使得声学手段无法在深度方向得到高精度结果,常由压力计提供深度信息参考。以4个声学基准同步测量目标的静态定位模型为例,当目标处于静止状态时,目标接收来自各基准声信号均为同一位置,各距离测量量交汇于一点,假设目标的三维坐标为XT=[xTyTzT]T,各基准的三维坐标为XBi=[xBiyBizBi]T(i=1,2,…,4),在深度信息先验已知条件下,静态目标定位模型的基本原理如图1所示。

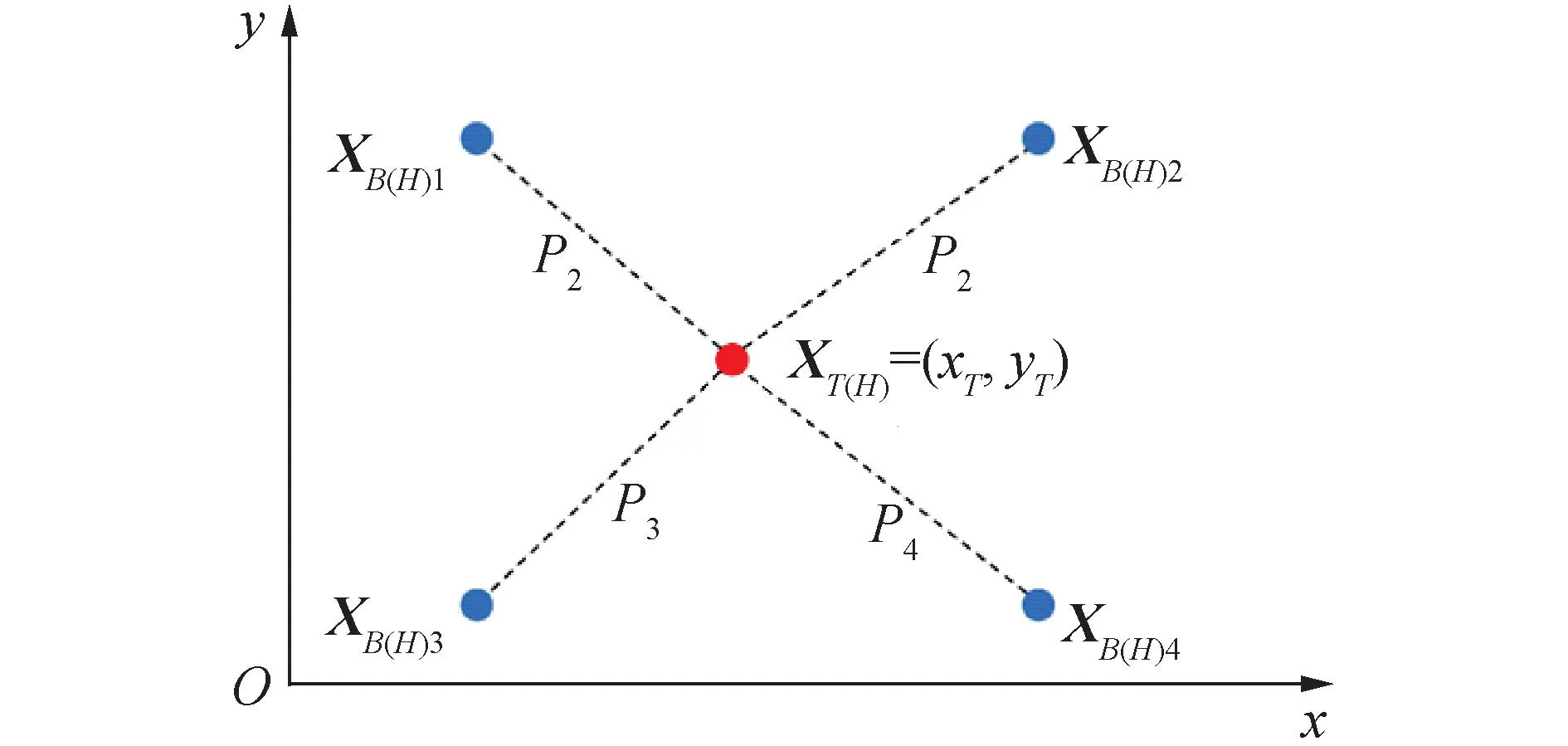
图1 定位导航基本原理Fig.1 Basic principles of positioning and navigation

利用距离交汇模型可列出观测方程:

(1)

式中:目标水平坐标XT(H)=(xT,yT);基准水平坐标XB(H)i=(xBi,yBi);Pi为水平测量距离;ti为目标到第i个基准到目标的测量时延;ci为第i个基准到目标的传播声速;深度差先验ΔZi=zT-zBi。

根据非线性最小二乘法,通过下式求得XT(H):

(2)

式中:X0为目标水平位置的初值;

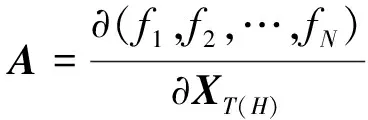
由式(2)可知,目标的定位误差ΔX主要由ΔR及A决定,ΔR为测距误差,与声速测量误差、时延测量误差以及深度误差有关;A与目标与海底基准之间的几何位置关系有关。

1.2 中远程定位导航难点分析

中远程条件下,基于声学基准的定位导航技术存在2个难点需要解决:1)声线翻转影响高精度测距问题,由射线声学理论可知,在中远程传播存在声线翻转,使得声速补偿困难,产生剩余测距误差;2)长传播延时引起的静态模型近似误差问题,由于声传播速度慢,当海底各声学基准发射定位声信号时,运动目标接收来自各基准定位声信号的时刻、位置均不同,引起静态模型失配,产生较大的定位误差。

1.2.1 声线翻转问题

声速在海水中呈垂直梯度分布,主要随深度方向变化。由射线声学理论可知,声信号在海水中传播满足Snell定律,声速的不均匀致使声线在不同深度层的传播中发生折射,最终形成一条弯曲传播路径而非直线。在中远程条件下,声线结构存在翻转现象,如图2所示,在南海3 000 m深声速剖面条件下,目标位于1 000 m深处,在与海底基准水平距离分别为5、10、15、20、25及30 km时,直达声线路径结构如图3所示,目标在大于15 km时接收到的均为翻转声线。

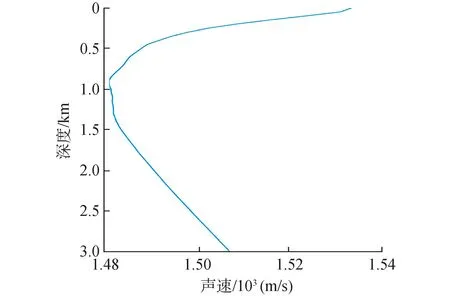
图2 南海3 000 m深声速剖面Fig.2 3 000 m sound velocity profile in the South China Sea

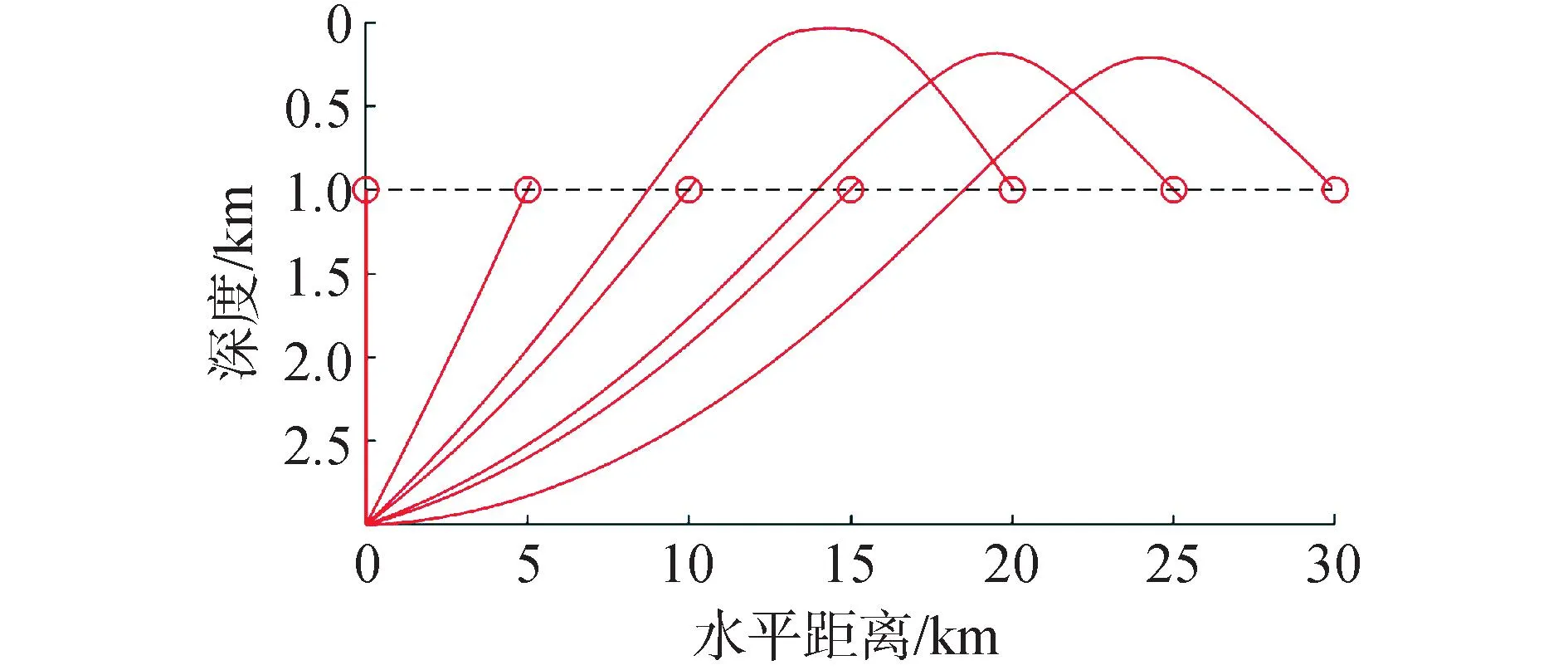
图3 不同水平距离下的声线结构Fig.3 Sound line structure at different horizontal distances

为分析声线翻转影响测距剩余误差变化特性,根据上述不同水平距离下声线结构,提取各点真实声速(目标与基准之间的欧拉距离除以真实时延),并与平均声速进行对比。平均声速的计算方法为:对声速剖面按深度进行分层,由目标和海底基准所在深度先验信息,统计声速剖面中相应深度分层范围内所有声速的平均值。对比结果如图4所示,当声线发生翻转时,平均声速与真实声速间的误差会急剧增大,可达数十米/秒量级,结合真实时延得出的测距误差甚至达到百米,严重影响中远程声学定位导航精度,故有必要结合实测声速剖面反演声线传播结构,修正声速信息。

图4 声速相关误差Fig.4 Sound velocity related error

通过上述分析可知,声线结构与相对几何关系相关,随着水平距离变大,直达声线会发生翻转。当声线发生翻转时,平均声速与真实声速间的误差会急剧增大,以平均声速作为目标至基准间的平均声速会带来较大的测距误差,故有必要结合声场实际传播环境计算有效声速。

1.2.2 长传播延时引起的静态模型近似误差问题

当海底基准定位导航运动目标时,如图5所示,海底各基准工作于同步模式,并在每个同步周期开始t0时刻发射定位声信号,由于目标与各海底基准之间的距离不同,目标接收来自各基准声信号的时刻、位置均不同,t表示时序轴,t1～t4分别为基准1～4信号到达目标时刻,X表示目标轨迹,x1～x4为对应t1～t4接收时刻目标位置。

图5 运动目标非共时、非共点接收示意Fig.5 Non-synchronous and non-collinear reception of motion targets

采用式(1)所示静态模型分析运动目标的定位误差结果如图6所示,横轴为运动目标距离海底基准阵中心的水平距离,纵轴为静态模型的水平定位误差。可见,水平定位误差随目标距阵中心距离变化,在20 km处可达数十米量级的定位误差。在深海、长传播延时条件下,目标运动引起的静态模型近似误差不可忽略,为了获得高精度的定位结果,须充分考虑目标运动的影响。

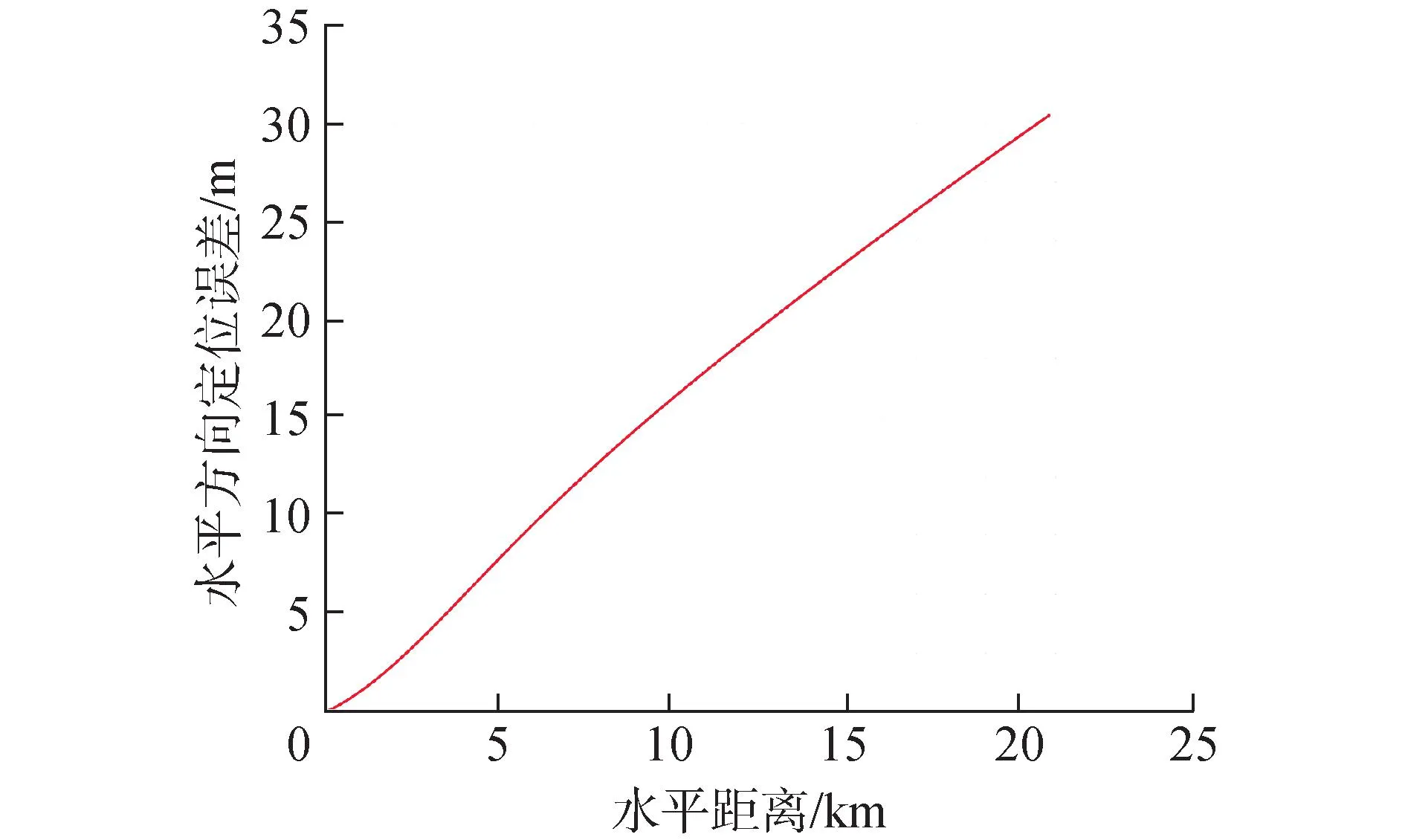
图6 运动目标静态模型定位误差Fig.6 Static model positioning error of motion targets

2 中远程声学定位导航方法

为克服海底基准中远程定位导航难点,实现运动目标中远程位置信息高精度测量,本文提出了一种基于海底基准的中远程声学PNT定位导航方法。该方法针对中远程直达声线翻转问题,基于射线声学理论,在深度先验条件下,对翻转声线进行分段跟踪处理以准确计算声速,消除剩余测距误差,同时针对长传播延时引起的静态模型近似误差问题,构建目标位置、速度联合解算模型,以补偿静态模型近似误差,实现了运动目标中远程高精度定位导航。

由于目标与各海底基准之间的距离不同,若考虑目标运动,则目标接收来自各基准声信号的时刻、位置均不同。假设各大地基准XBi在每个定位周期开始时刻发射声信号,目标在经传播时延tri接收到来自第i个基准的声信号,对应的接收时刻坐标为Xri。则通过测距关系可得到接收位置与大地基准间的观测方程:

‖Xri-XBi‖=ceff(i)tri

(3)

将每个定位周期开始时刻目标位置作为待定位置,则对第i个声信标而言,可通过一个位置偏移量进行归算,有Xri=XS+ΔXi。XS=(xs,ys,zs)为定位周期开始时刻的目标位置;ΔXi为目标接收到第i个基准信号时刻位置与定位周期开始时刻的位置偏移量,ΔXi=(Δxi,Δyi,Δzi);ceff(i)为目标接收第i个基准信号时刻位置与第i个基准间的声速。

在深度先验条件下,本文所述联合解算模型的观测方程可改写为:

‖XS(H)+ΔX(H)i-XB(H)i‖=Ri

(4)

位置偏移量ΔXi可通过目标速度与目标航行时间的乘积计算得到。在仅有声学测量时延条件下,目标运动速度v无法通过其他速度源提供。假定目标运动状态为缓变运动过程,则静态模型解算结果为同一定位周期的一系列接收时刻的坐标的加权平均,结合定位周期T,第k个周期的平均速度计算方式为:

位置偏移量ΔXi=v·tri,v表示目标运动速度。

令fi(XS(H))=‖XS(H)+ΔX(H)i-XB(H)i‖,有:

记:

则f1,f2,…,fN对∂XS(H)的雅克比矩阵为:

此处采用高斯牛顿法求解上述联合模型,迭代渐次修正目标位置、运动速度,XS(H)的迭代公式为:

XS(H)=XT(H)+(JTJ)-1JTBT

式中:XT(H)为目标水平坐标的初值;

同时,声速ceff的计算基于射线声学理论和声速剖面c(z),声线由深度zs传播到深度zr的传播时间及传播的水平距离为[10]:

(5)

(6)

式中:n为snell常数;c(p)为深度z处的声速值。

当声源与接收点的位置已知时,只需确定声源处直达声的初始掠射角,即可唯一确定直达声的轨迹。当目标与基准间的声线为翻转直达声时,需对声线的水平传播距离进行分层、分段跟踪计算。假设翻转点的深度zt,则翻转声线的水平传播距离可表示为:

(7)

式中:Ns、Nr及Nt分别为海底基准深度zs、目标深度zr及翻转深度zt对应的层数;am为非翻转声线段第m层的绝对声速梯度;an为非翻转声线段第n层的绝对声速梯度;θm为非翻转声线段第m层的入射角;θn为翻转声线段第n层的入射角。

采用二分法计算入射角θ0,使目标与基准之间的水平距离逐步逼近定位结果所计算的水平距离R:

在迭代获得翻转声线的初始入射角后,可通过下式分段计算翻转声线的传播时延:

(8)

最后根据下式计算目标与基准对应的声速:

(9)

下面给出了基于海底基准的中远程声学PNT定位导航方法的算法流程,其中目标函数定义为观测残差的平方和,ε=BBT。

算法输入量:海底基准位置XBi、传播时延tri、声速剖面c(z)、定位周期T、目标深度zs。

算法输出量:定位周期开始时刻的位置XS。

1)静态定位模型计算目标运动轨迹XT,并结合XBi、zs计算声速的初值ceff0(i)

WHILE(1)

2)根据XT计算ΔXi

WHILE(1)

3)根据XT、ceff0(i)计算目标函数值ε0

4)将观测方程线性化,并计算用户终端位置的更新值XS(H)

5)根据XS(H)、XBi以及声速剖面c(z)重新计算新位置对应的声速ceff(i)

6)根据XS(H)、ceff(i)计算新的目标函数值ε1

7)若|ε0-ε1|<Δ1,输出XS=XT;否则,令XT=XS,ceff0(i)=ceff(i),并跳至步骤3;

END

8)若‖XS-XT‖<Δ2,输出XS;否则,令XT=XS,并跳至步骤2。

END

3 海底基准系统性能验证

3.1 中远程海底基准系统

3.1.1 系统组成及功能

中远程海底基准系统由海底基准和用户终端2个部分组成,如图7所示。海底基准搭载2～4 kHz声信标,由2～4 kHz换能器、信号发射单元以及供电单元构成,在海底工作值守期间能够以同步工作模式广播声学定位信号,与水下用户进行声学信息交互。水下用户搭载2～4 kHz用户终端,由2～4 kHz换能器和信号处理单元构成,能够采集海底基准广播的2～4 kHz定位声信号并解析为时延信息,满足水下用户的定位导航需求。

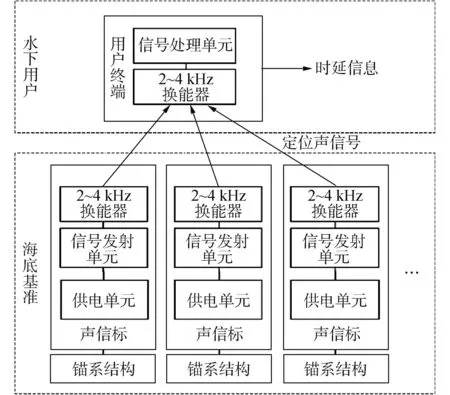
图7 系统组成Fig.7 System composition diagram

3.1.2 声学定位导航信号设计

海底基准系统为获得高处理增益和测距精度,通常采用宽带信号,系统采用直接序列扩频信号作为定位信号。受益于直扩信号强抗干扰能力和多发射机可同频、同时工作特性。该信号由单频载波和伪随机噪声码(PRN码)2个部分组成,信号结构如图8所示。PRN码采用255码长的Kasami随机噪声码,码生成方式见文献[20]。

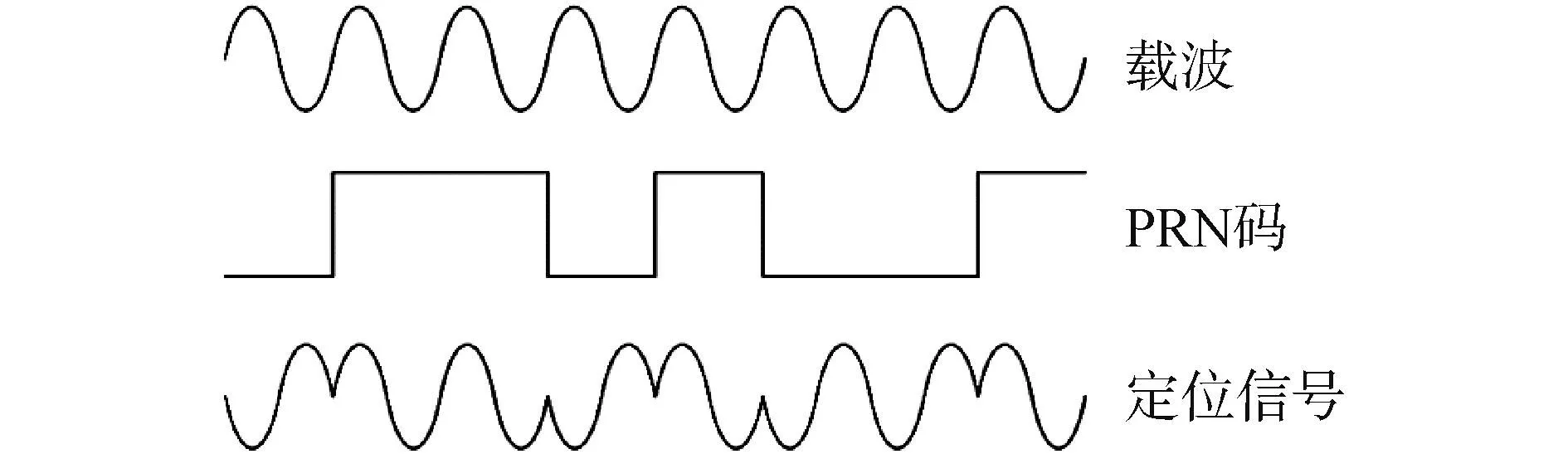
图8 定位信号结构Fig.8 Positioning signal structure diagram

声学定位导航信号基本参数设计:载波频率为3 kHz,频带覆盖范围为2～4 kHz,带宽为2 kHz,脉冲宽度为127.5 ms,采样率为48 kHz。

3.2 海上试验

3.2.1 海试概述

2023年4月于中国南海开展了中远程海底基准系统性能验证试验。试验系统由测量船、深拖和海底基准3个部分组成,总体实验场景如图9所示,测量船由阵中心向外航行拖曳深拖,航行期间4个海底基准以同步工作模式广播定位声信号,深拖上的声学用户终端采集信号,为深拖定位导航提供时延测量信息,同时测量船实时定位监控深拖,获取深拖位置信息参考真值。试验系统实物如图10所示,系统组成及功能具体见表1。

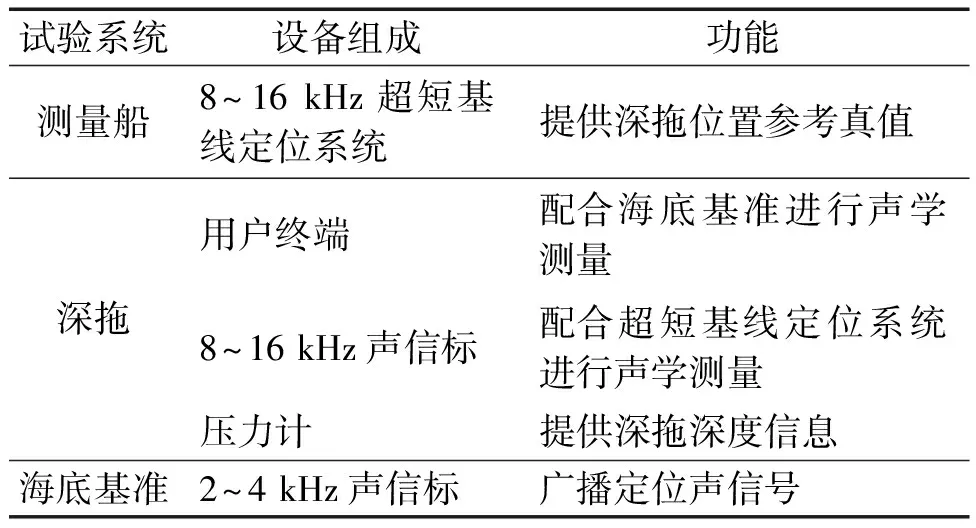
表1 试验系统组成及功能Table 1 Composition and functions of the testing system

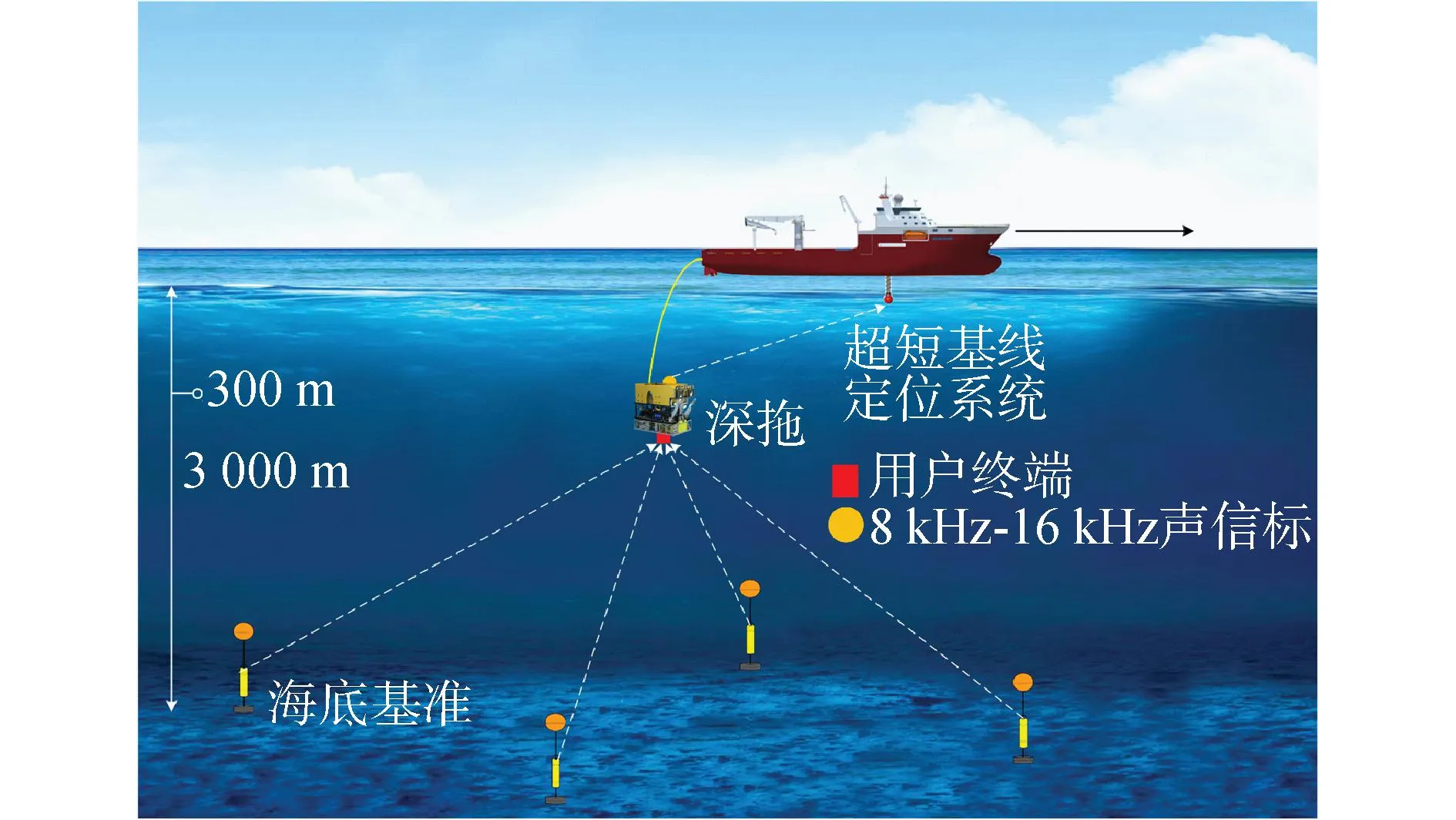
图9 海试场景图Fig.9 Scene graph of offshore test

图10 系统实物Fig.10 System physical diagram

试验系统的总体几何关系如图11所示,深拖定位导航测线长度约20 km,覆盖深度100～450 m。以阵中心为原点,4个2～4 kHz声信标坐标的水平坐标和高程见表2。

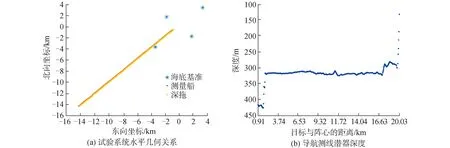
图11 试验系统总体关系Fig.11 Overall relationship diagram of the test system

3.2.2 真值系统

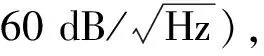
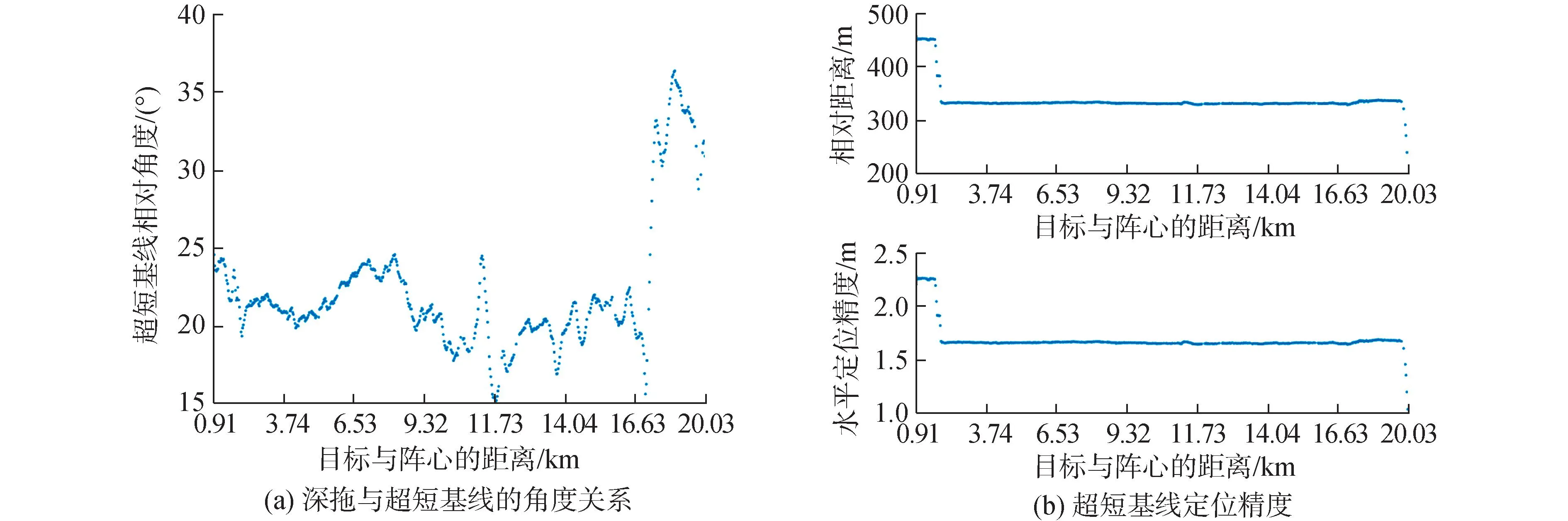
图12 超短基线定位精度统计Fig.12 Statistics of ultra short baseline positioning accuracy

为证实超短基线可作为外符合精度评定依据,利用本文所提出的方法计算测距残差,并结合海底基准与深拖坐标的水平几何精度因子(horizontal dilution of precision,HDOP)[21]计算理论定位精度。水平方向理论精度δH计算式为:

(10)

式中:δx为x方向理论定位精度;δy为y方向理论定位精度;K为观测方程的雅克比矩阵;δr为测距残差的精度。

理论精度计算结果如图13所示,在距离阵中心20 km处的理论定位精度为12.33 m,与超短基线2.5 m定位精度差一个数量级,因此超短基线的定位结果可以作为海底基准中远程定位导航的真值参考。

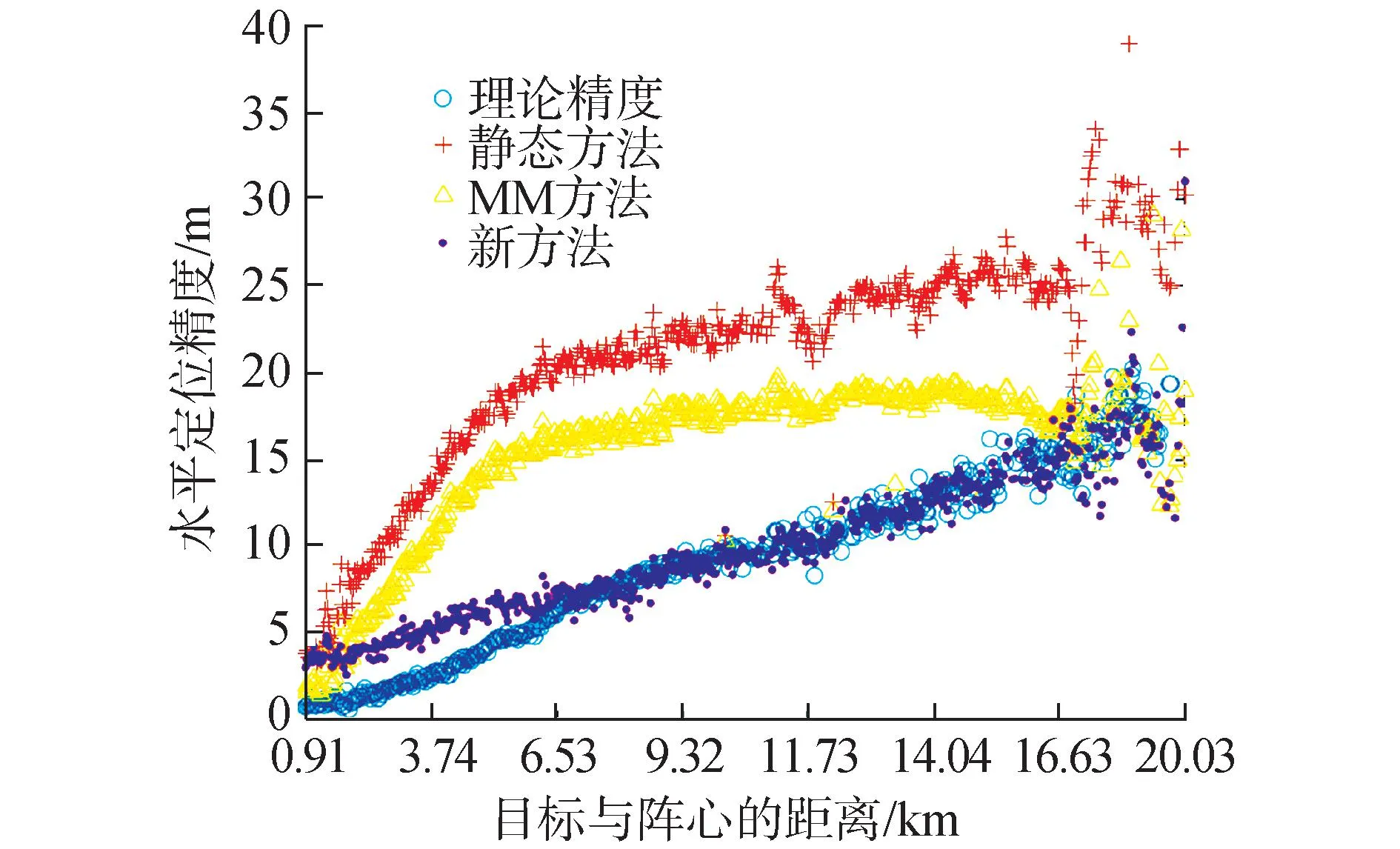
图13 不同方法的定位导航精度Fig.13 Positioning and navigation accuracy of different methods

3.2.3 数据处理

基于海试采集的导航测线数据,利用本文所提出的中远程声学定位导航方法,计算中远程海底基准系统对深拖的定位导航结果,以超短基线参考真值评定其定位精度。进一步地,通过对比静态方法和MM方法证明本文方法的优势。

静态方法定位原理见1.1节,MM方法是在静态方法的基础上,首先通过初始不少于3个定位周期的静态定位结果建立目标坐标与时刻的近似函数关系,以提供后续周期的目标先验位置,通过引入测时修正量改正静止模型中对声学测时数据的不准确使用问题,将测时修正量作为新增未知模型参数与目标坐标进行联合估计,补偿目标声源的运动影响。

3种定位方法结果与超短基线参考真值对比的外符合精度结果如下图所示,各方法水平定位精度的RMSE统计结果见表3,本文方法定位性能最优,其定位精度随目标与阵心的距离增大而减小,在精度变化趋势规律和数值量级与理论精度一致性好。

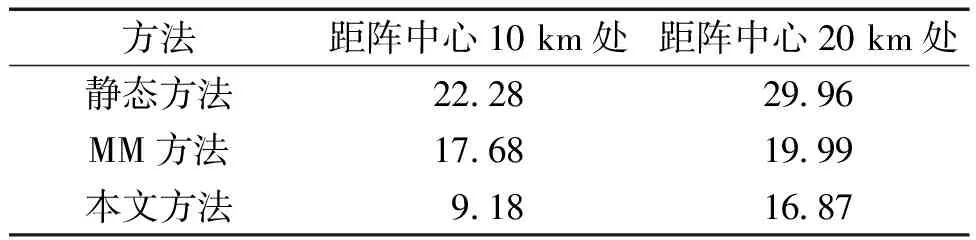
表3 水平定位精度统计Table 3 Horizontal positioning accuracy statistics

表4 内符合精度统计Table 4 Inside accuracy statistics

3种方法的内符合定位导航精度统计结果为:本文方法的内符合精度为9.94 m,优于静态方法的14.76 m和MM方法的13.99 m。

由海试结果可知,本文方法的定位精度量级和趋势符合理论规律,内符合、外符合精度均优于静态方法和MM方法。MM方法在静态方法上进行运动补偿,在距阵中心20 km时,将29.96 m的定位精度提升至19.99 m,本文方法同时对运动模型和声速进行补偿、修正,进一步实现了16.87 m的定位精度,满足深海中远程定位导航性能需求。

4 结论

1)联合目标位置、速度的动态导航模型的理论定位精度与以超短基线定位结果作为外符合精度的量级和趋势近似一致。

2)联合目标位置、速度的动态导航模型在20 km的外符合定位导航精度为16.87 m,优于静态方法的29.96 m 和MM方法的19.99 m。

本文成果对深海水下定位导航应用模式和海底基准的远程定位导航技术等相关研究的开展提供了新的研究思路。