基于因子图模型的水下传感器网络时间同步方法
孙大军, 欧阳雨洁, 韩云峰, 王泽彧, 刘璐
(1.哈尔滨工程大学 水声技术全国重点实验室, 黑龙江 哈尔滨 150001; 2.海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001; 3.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001)
统一的时间基准是水下传感器网络协同合作的基础,随着对水下节点工作时长要求的提高,时钟漂移不可避免。在不回收节点的前提下,水下时间同步方法是修正节点时钟的必要手段。现有时间同步算法大多致力于消除节点移动带来的影响,从而更好地估计钟差。例如Chirdchoo等[1]针对水下节点移动带来的时延时变性,提出了水下移动网络时间同步协议(time synchronization protocol for underwater mobile networks,MU-Sync)算法,该算法通过多次双向交互完成同步。但MU-Sync假设单向传播延迟为往返时间的一半,当节点快速移动或待同步节点响应时间过长时,都会造成较大的误差。文献[2-4]在文献[1]的基础上,通过多次交互预测节点移动速度从而分别估计往返传播时延,消除移动对时间同步的影响。但其移动速度估计精度较低,且同步流程较长。
Lu等[5]通过测量信号多普频移估计相对运动速度,设计了基于多普勒的移动水下传感器网络时间同步(Doppler-based time synchronization for mobile underwater sensor networks,D-Sync)算法,进一步提高了相对速度的估计精度,从而提高时间同步精度。Liu等[6]在D-Sync基础上提出了一种用于移动传感器网络的多普勒辅助时间同步方案(a Doppler-assisted time-synchronization scheme for mobile underwater sensor networks,DA-Sync)算法,该算法在估计多普勒尺度因子时加入了时钟偏斜的影响,由估计出的多普勒频移计算相对速度,并利用卡尔曼滤波进行速度细化,补偿了由时钟偏斜引起的估计误差。Zhou等[7]考虑节点移动性和时钟偏斜影响的同时,用多普勒尺度因子代替了节点间的相对运动速度,提出了一种用于移动水下传感器网络的多普勒增强时间同步(a Doppler-enhanced time synchronization for mobile underwater sensor networks,DE-Sync) 算法。相比于DA-Sync,简化了线性回归流程,且算法不涉及声速计算,提高了时间同步精度。但多普勒估计类的时间同步算法大多假设参考节点与待同步节点之间的相对速度呈线性变化,这在实际水下环境中较难实现。且同步流程上依旧是多次双向交互的模式,交互周期长,同步效率低。
综上,现有时间同步方法均以目标位置未知为前提,尽可能提升时间同步的估计精度。这往往意味着更多的交互次数,更复杂的信号形式以及更复杂的计算流程。然而大部分情况下,作为水下传感器节点,无论是可移动的潜器,或是静止的水下信标,其本身具备一定的位置信息获取能力,若将位置信息与声速信息的融合,可以简化时间同步流程。在位置信息精度较高时可以获取更高的时间同步精度。
因子图模型[8]作为概率图模型的一种通用表现形式,因其对多变量之间复杂关系的强大处理能力,而广泛应用于水下目标检测与跟踪、水下通信、水下声呐信号处理、水下环境感知、水下机器人导航与控制等领域[9-14],但在水下授时领域还未有成熟的研究成果。现有水下时间同步方法大多聚焦于消除节点运动性对时延估计的影响,忽略了利用位置信息已知的水下节点(例如:水下基准站、配备高精度惯导的潜器等)简化授时模型的可能性。对此,本文提出了一种基于因子图模型的水下传感器网络时间同步方法(简称概率图法),在保障同步精度不低于现有方法的基础上,实现了时间同步过程的优化。每次同步仅需各节点发声一次,同步周期远小于现有方法;由于交互流程的不同,相较于现有方法,每次交互均可实现全传感器网络的时间基准统一,同步效率大大提升;二进制简化计算后,计算效率提高。
1 概率图法算法原理
1.1 因子图模型
因子图是一种能够双向传递的图模型,它具有把单个复杂的多参数的整体联合函数表示成任意局部变量分布函数相乘的形式。如果选择分解的局部函数只有简单的几个变量组成,可以减少计算的复杂性。因子图的结构得到确定后,可通过消息的传递与更新来进行计算,即和积算法[8]。大多数对于因子图的探索与研究都集中在2个方面。一种是求解变量的边缘函数分布,通常用于通信工程等相关领域。另外一种是整体状态估计,通常用于图像识别等相关领域。对于解决时间同步问题,需要获取钟差变量的边缘概率密度函数,并基于概率密度函数进行加权平均,获得最终的钟差变量估计结果。
概率图法一般应用于水下基准网络布放或维护时,此时基准具备一定的位置初值,可以通过相对测距实现时间基准的统一。融合参数包括:基准位置信息、基准钟差、相对测距信息、时延差测量信息、相对测距信号接收时刻。此时全局函数表示为:
p(Φ,T,τ,D,P)=p(Φ,T,τ)p(τ,D)p(D,P)
(1)
式中:Φ表示各基准钟差集合;T表示所有测量信号接收时刻集合;τ表示时延差测量值集合;D表示测距的集合;P水下基准位置集合。
以3个信标A,B,C(A为参考信标,ΦA=0)间的互测距为例,因子图模型如图1。图1中,f1表示基准接收信号时刻、时延差与基准钟差间的关系,f2表示测距信息与时延差之间的函数关系,f3表示测距信息与基准位置之间的函数关系。Φi表示基准i的钟差,Tij表示基准i测量基准j的互测距信号的接收时刻,τij表示基准i与j的时延差测量值,Dij表示基准i与j距离测量值,Pi表示水下基准i的位置。
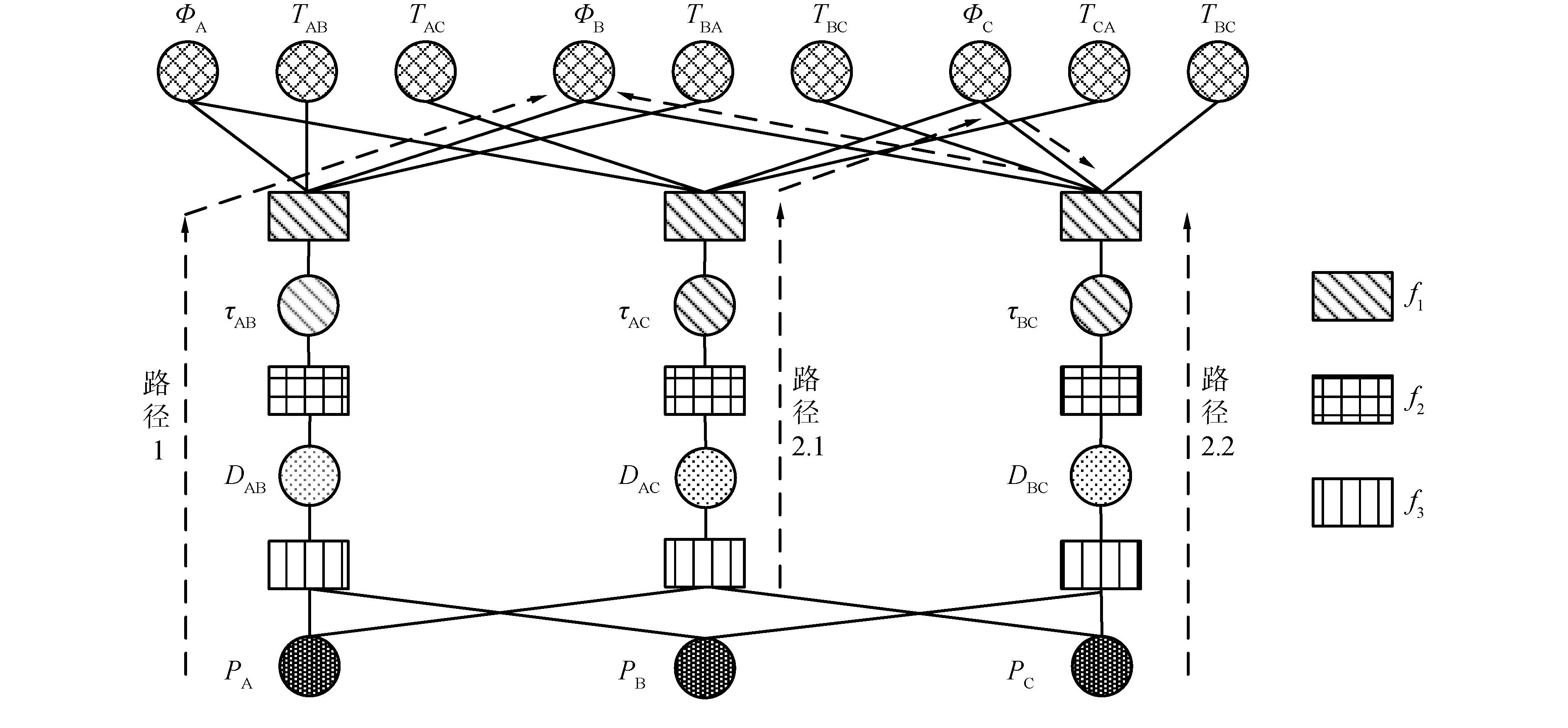
图1 水下基准时间统一时的因子图模型及消息传递路径Fig.1 Factor graph model and message transmission path for unified underwater baseline time
本文以基准B的钟差为例,描述其边缘概率密度函数。由图1的因子图可知,消息传递至节点ΦB共包含3条路径,分别为路径1、路径2.1、路径2.2。综合考虑各路径的概率转移过程[13],可得到以下关于钟差ΦB的边缘概率密度函数:
p(ΦB)=(fa(ΦB|ΦA)fb(τAB)fc(DAB))·
(fa(ΦB|ΦC)fb(τBC)fc(DBC)·
(fa(ΦC|ΦA)fb(τAC)fc(DAC)))
(2)
其中:
(3)
i,j∈{A,B,C}i≠j
对于第i个基准的钟差Φi,一般可建模为[14]:
Φi=Tij+Tji+2εT-τij-Φj
(4)
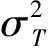
(5)
第i及第j个基准间的互测距信息D与时延差信息τij存在[15]:
(6)
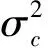
(7)
此外,基于距离交汇原理,第i及第j个基准的位置Pi、Pj,及它们之间的距离满足:
Dij=‖Pi-Pj+2εp‖
(8)
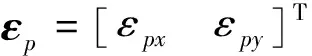
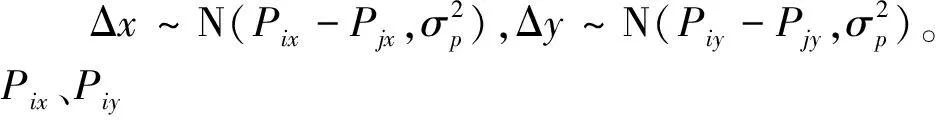
令u=(Δx)2+(Δy)2,λ=(Pix-Pjx)2+(Piy-Pjy)2,易知u服从自由度n为3的非中心卡方分布:
(9)
(10)
参考基准B的推导,同理可得关于基准C钟差ΦC的边缘概率密度函数。
正常情况下,待求目标的位置、距离、时延、钟差等信息为连续分布,变量间的相互关联函数也为连续分布。通过对连续分布函数求期望的方式估计钟差Φi,计算复杂度较高。故引入采样思想完成对连续分布函数的离散化。
将钟差分布的最大可能区域划分为网格,每个网格代表一个钟差估计值。通过对每一个网格的估计值进行加权平均,获得钟差的最终估计结果。权值的主要计算步骤为:如果测量的数据集合Q已知,可以用间隔固定的距离散点来代表网格区域(X=x,Y=y)。通过x,y位置处概率密度函数f的值代表此网格区域的权重w=f(X=x,Y=y|Q)。
1.2 二进制简化
因子图的计算主要集中在消息的传递与更新的上。为了降低复杂度,本文采用二进制的模式进行消息的传递。二进制模式将消息传递过程中的和运算变成逻辑或运算,乘积运算转化逻辑与运算,降低运算的计算量。
基于二进制模式,距离信息的概率密度函数可简化为:
(11)
时延信息的概率密度分布函数可简化为:
(12)
节点空间相关函数可简化为:
(13)
εd、ετ、εΦ分别表示各概率密度函数的标准差。消息的传递表示为:
(14)
本节针对水下基准间的时间同步场景,建立因子图模型之后采用和积算法计算边缘概率函数。最后,简化计算过程,采用离散化二进制来计算。
简化后算法伪代码如下所示。
算法1 钟差估计算法
Procedure Estimated clock bias(
pA,p1,…,pn//参考节点A以及n个待同步节点
c,T(n+1)×n//声速以及互测距观测值
σp,σc,σT//位置,声速,时刻观测值精度)
1){pi,pj}←选取任意两点{p1,…,pn}
//计算ΦA=0时i节点钟差,路径1。
3)στ,σΦ←同理
4)对所有的{pA,pi}有DAi满足式(11)
5)对所有的DAi有τAi满足式(12)
6)对所有的τAi有Φi|A满足式(13)
//计算ΦA=0时j节点钟差,路径2.1
7)Φj|A←同步骤2)~6)
//计算集合Φj|A下,i节点钟差,路径2.2
8)对φk,|jA,φk,j|A∈Φj|A
9)Φk,i|j同步骤2)~6)
//计算i节点最终钟差
END
1.3 计算复杂度分析
2 仿真分析
2.1 分辨力对同步结果的影响
和积算法在因子图上运行是基于离散分布的。需要对连续分布函数进行采样转化为离散分布。将待测目标分布的最大可能区域划分为网格,分辨力定义为网格边长的大小,x轴、y轴的长度相等。为了降低复杂度,本文采用二进制的模式进行消息的传递。由式(11)~(13)可以看出,εd、ετ、εΦ等标准差是算法简化后,同步精度的主要影响因素,分辨力的选取应小于各标准差。
以钟差分辨力为例,当时延测量精度为2×10-5s时,分别将分辨力设置为1×10-6、5×10-6、1×10-5、2×10-5、3×10-5、4×10-5s比较时间同步结果。如图2所示,钟差估计精度随分辨力提升而提升,但估计准确度却未发生变化。且当分辨力大于时延估计精度2×10-5s时,估计精度下降,且频率(出现次数)也随之下降,分辨力降低到4×10-5s时无法搜索到结果。

图2 分辨力对同步结果的影响Fig.2 Impact of resolution on synchronization results
2.2 时刻测量误差对同步结果的影响
由式(5)可知时刻测量精度直接影响钟差估计精度。时刻测量精度越高,钟差估计精度越高,直至测量精度逐渐趋近钟差分辨力,如图3所示。趋于分辨力后,虽然峰宽依旧下降,但精度维持不变。此时输入的声速误差与位置误差分别为0.5 m/s、10 m。
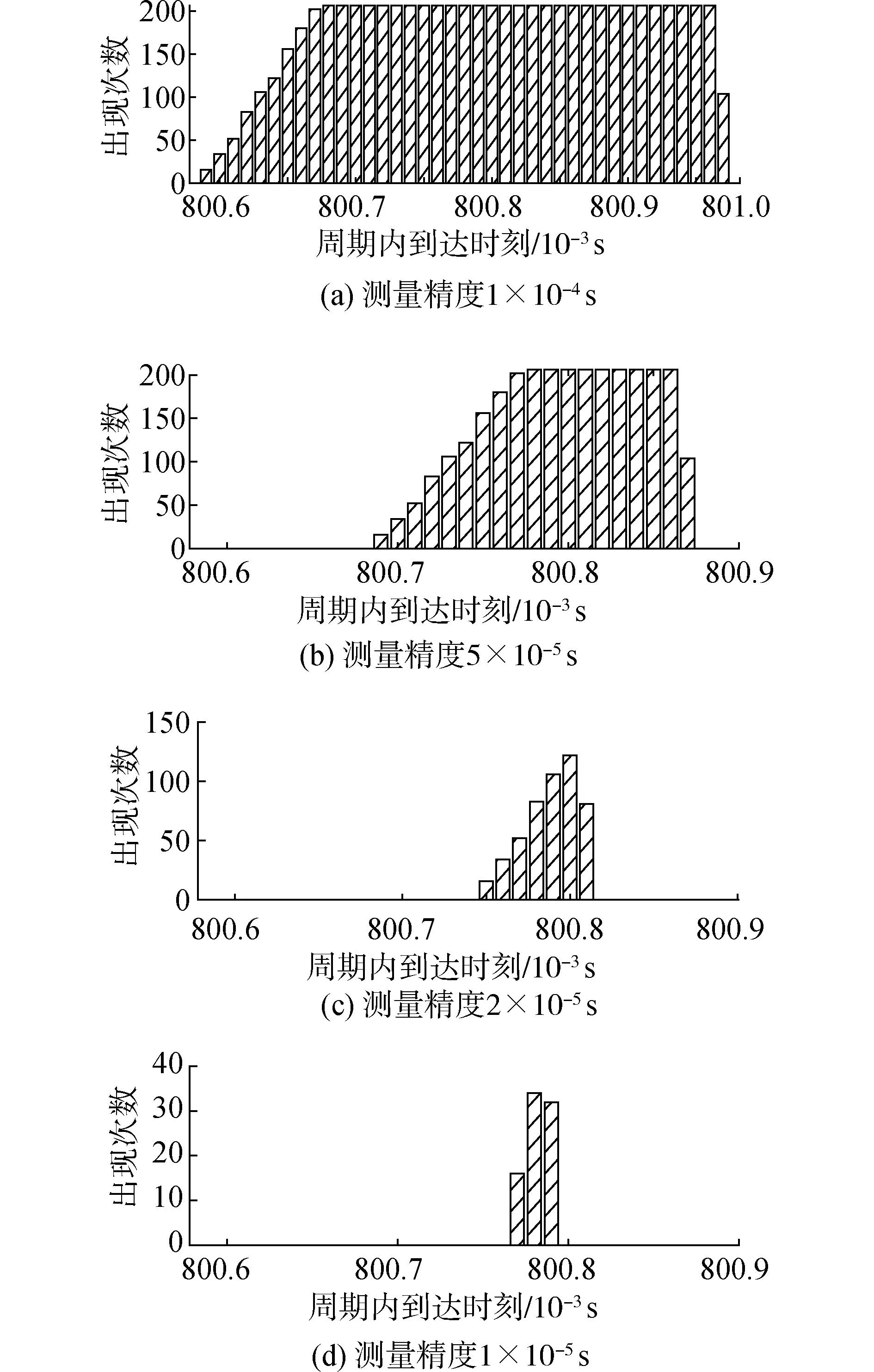
图3 时刻估计精度对同步结果的影响Fig.3 Impact of time estimation accuracy on synchronization results
2.3 与DE同步方法的精度对比
由于DE方法主要应用于运动目标,概率图法主要应用于静态或低速的水下基准网络,所以本节将同时对运动目标与静态目标进行仿真模拟。仿真条件设置为:交互周期4 s,交互次数60,每次交互包括一次参考节点的同步请求和一次待同步节点的同步应答。全程耗时4 min,节点轨迹如图4所示。参考节点与待同步节点深度差为50 m。
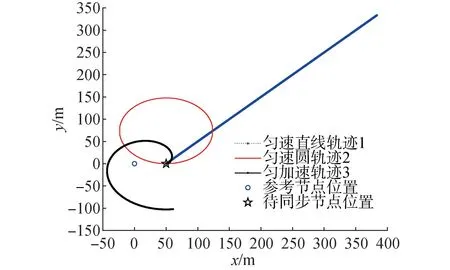
图4 目标节点轨迹Fig.4 Target node trajectory
图5所示,目标节点以2 m/s(一般试验船作业时的平均速度)的速度做匀速直线运动时,DE[7]同步方法与概率图法估计精度对比,显然概率图法整体精度较高。轨迹2为速度2 m/s的匀速圆周运动,轨迹3为初速度为0、加速度0.012 m/s2的任意运动。
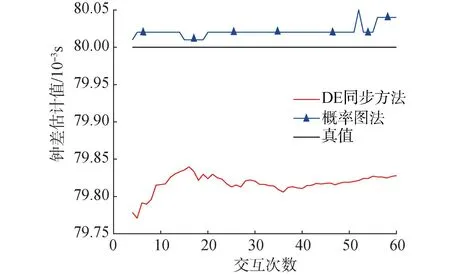
图5 轨迹1下DE与概率图法估计精度对比Fig.5 Comparison of DE and probability plot estimation accuracy under trajectory 1
由图6、7可知,轨迹2和3下概率图法的精度明显优于DE-Sync方法。单次交互中,概率图法仅需参考节点单向同步请求信息即可,同步效率提高50%以上,且无需应答,交互时间进一步压缩。考虑概率图法主要应用于静态或低速网络,进一步模拟了静态目标下两者的性能。交互周期和流程不变,参考节点与待同步节点起始相对位置不变,待同步节点速度为零,位置小幅扰动。
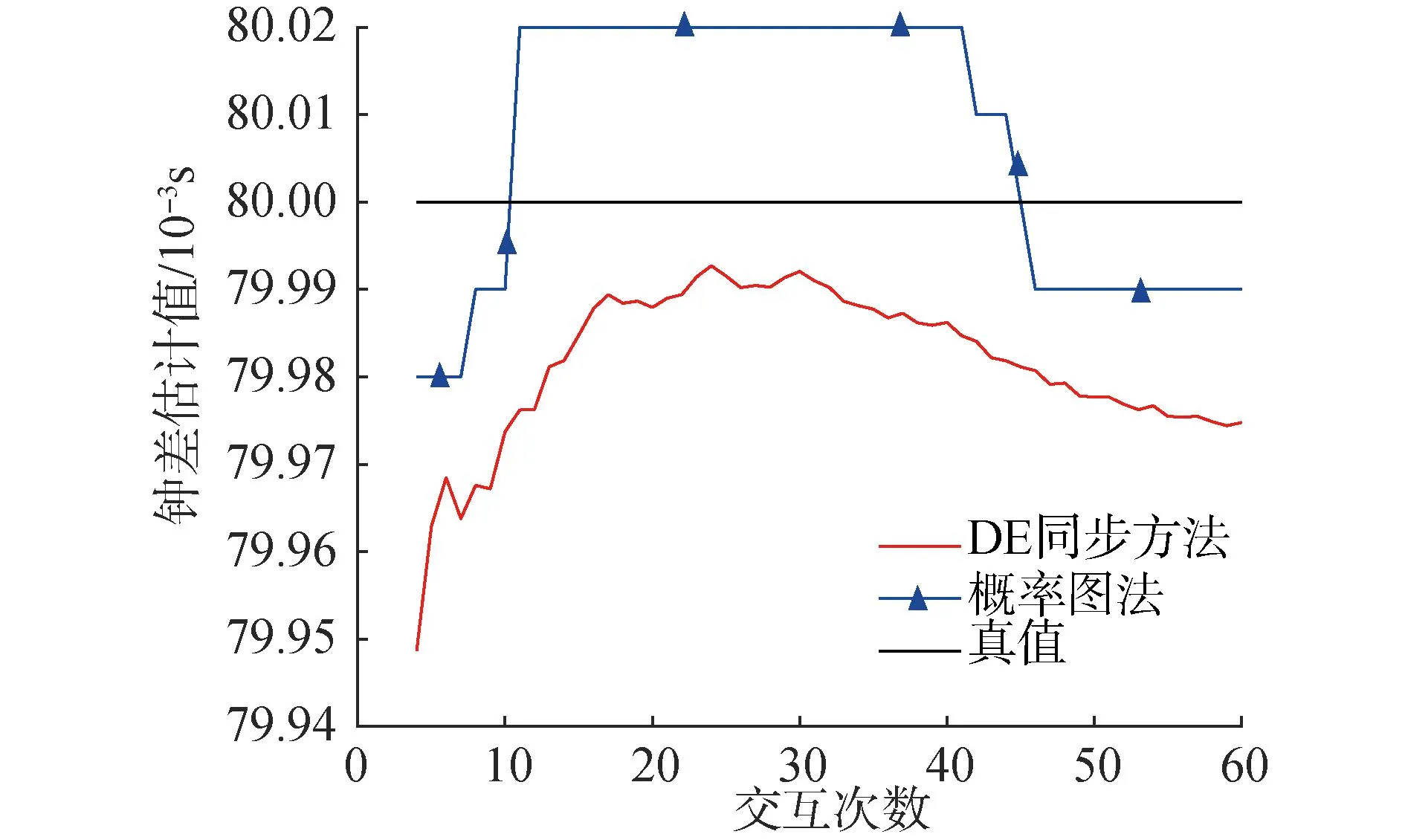
图6 轨迹2下DE与概率图法估计精度对比Fig.6 Comparison of DE and probability plot estimation accuracy under trajectory 2
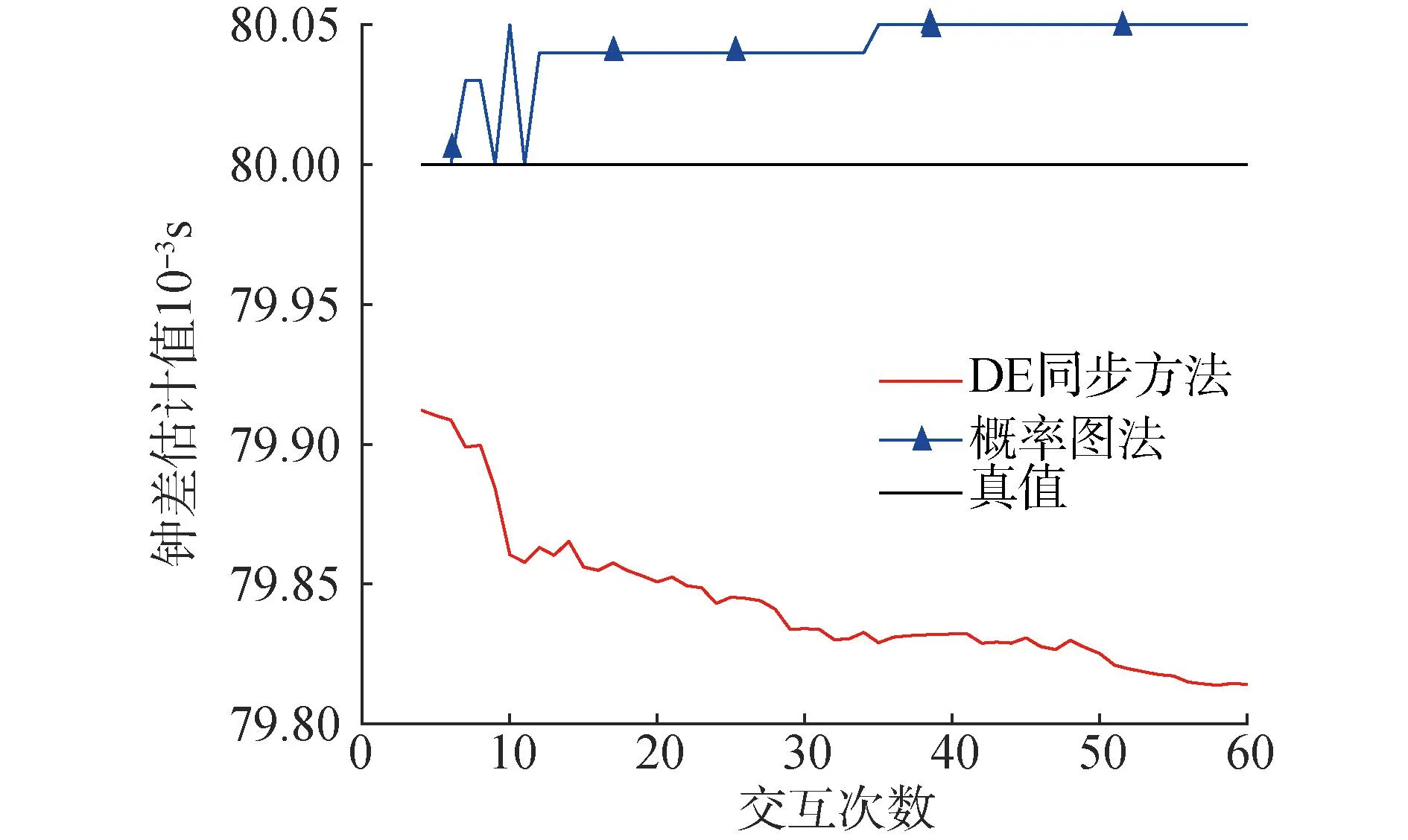
图7 轨迹3下DE与概率图法估计精度对比Fig.7 Comparison of DE and probability plot estimation accuracy under trajectory 3
从图8可知,静态目标下,概率法的准确度更高。对于水下传感器网络,单向交互即可完成同步。相较于现有方法在大规模水下节点授时具备极大优势。
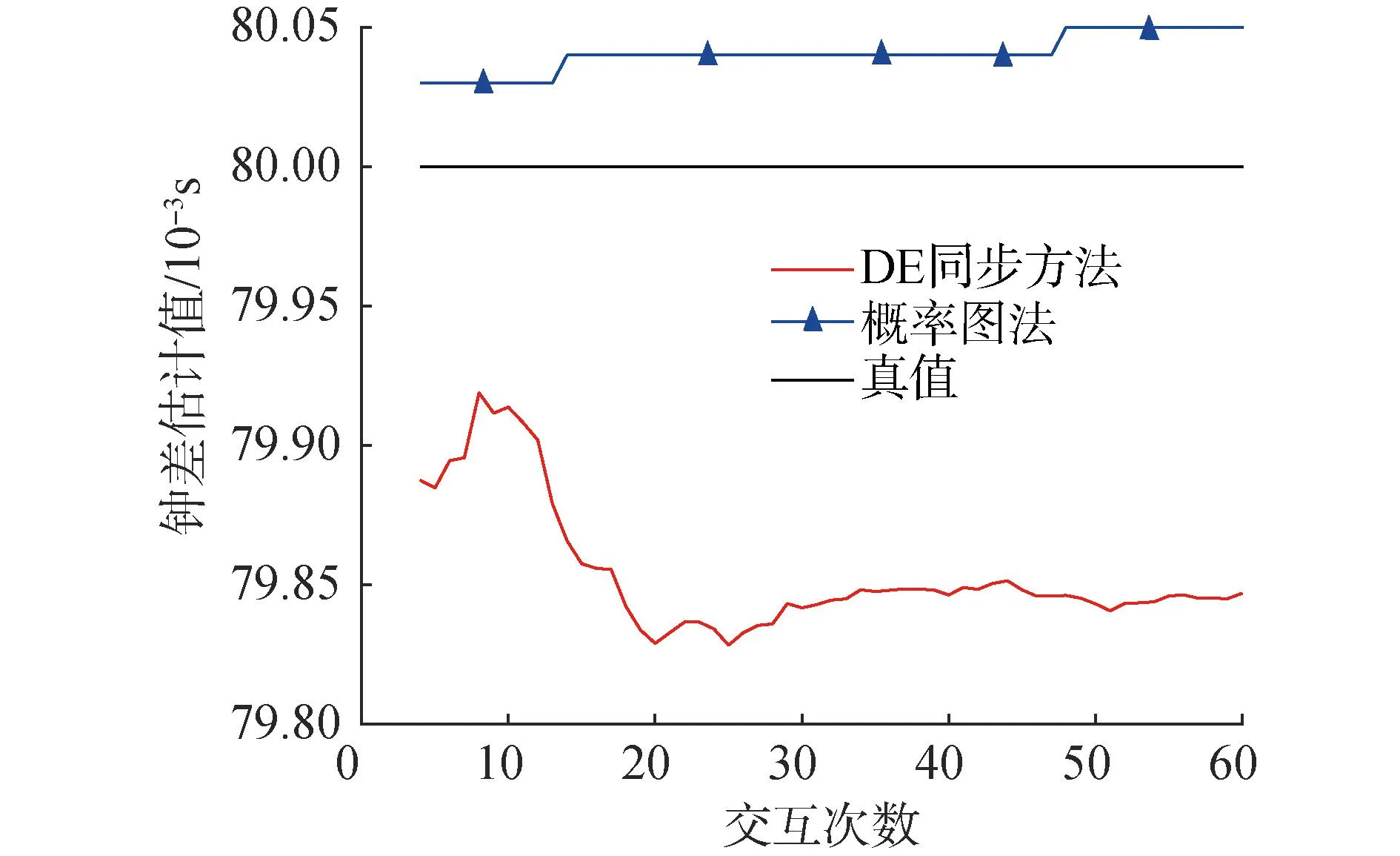
图8 静态目标下 DE与概率图法估计精度对比Fig.8 Comparison of DE and probability plot estimation accuracy under static targets
2.4 计算复杂度对比
1.3节给出了计算复杂度的理论分析,本节则会直接给出实际运算时,计算时长与处理数据大小的关系。如图9所示,随着交互次数的增加,DE方法的计算时间迅速上升,而概率图法变化平缓。
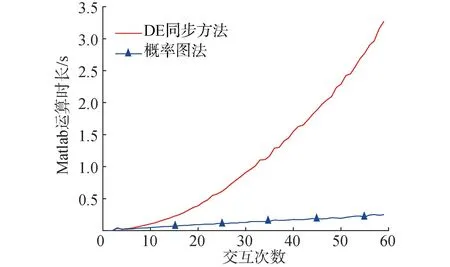
图9 时刻估计精度对同步结果的影响Fig.9 Impact of time estimation accuracy on synchronization results
综上可知,分辨力作为因子图模型离散化的重要参数,其值越大,估计精度越低,值越小,计算复杂度越高,所以其取值略高于时延测量精度即可。输入参数的测量精度,在二进制简化计算过程后,测量进度会直接影响搜索范围,所以输入参数应尽可能包含输入参数真值,但过低的精度也会导致计算量的增大。概率图法的估计精度与现有方法处于一个量级,但同步效率远高于现有方法。此外概率图法的计算复杂度低于现有方法,且随着数据量的增加,差距进一步加大。
3 试验数据处理
3.1 试验概况
为了验证概率图法在水下基准网络中的同步性能,于2023年4月3日10时58分南海3 400 m海试海域进行了水下基准网络时间同步试验。试验共布放并标定了4支海底基准信标,总时长3 h。通信信号频带为2~4 kHz,信标布放位置关系如图10所示(信标J3由于电量耗尽,数据采集部分缺失,后续不参与数据处理)。
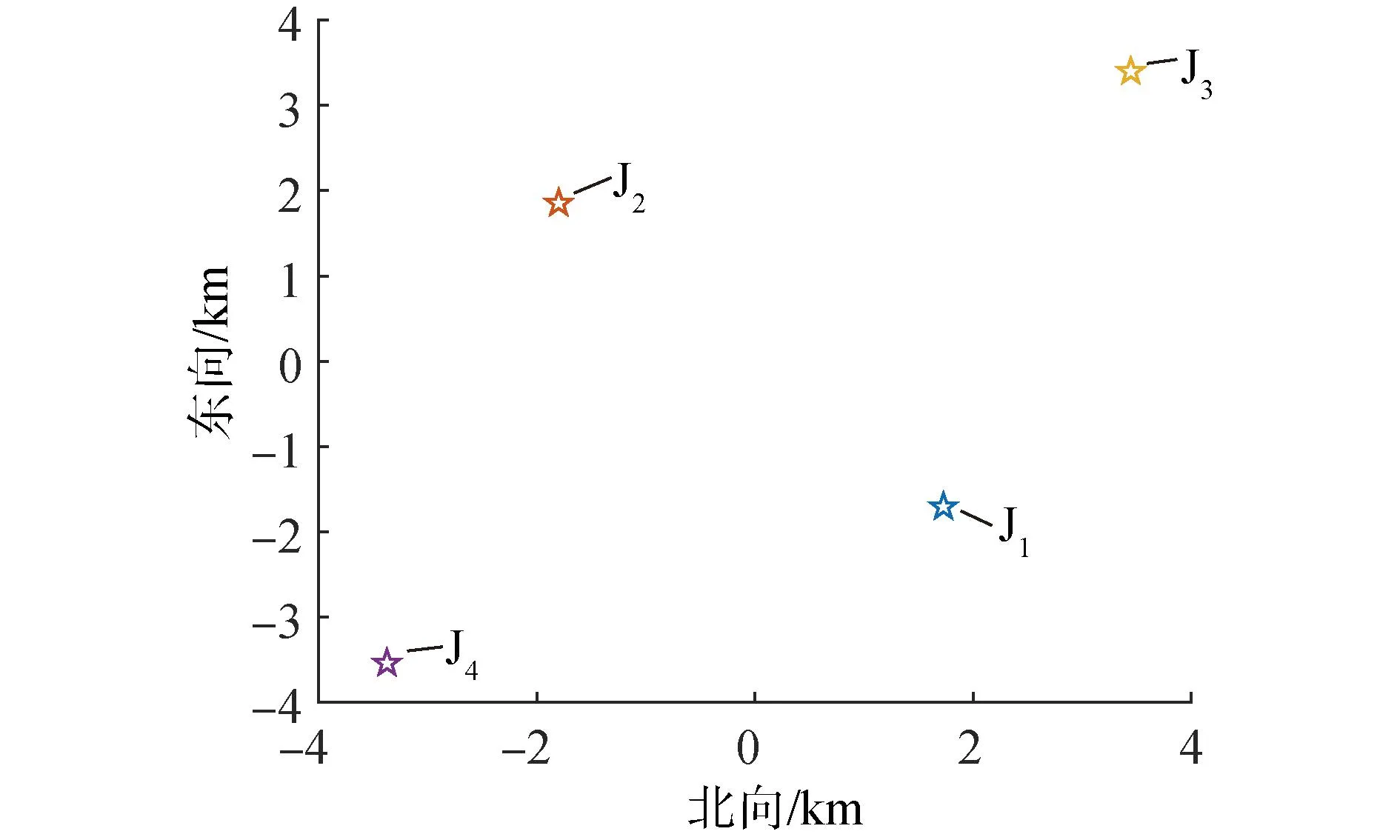
图10 海试信标位置示意Fig.10 Location diagram of sea trial beacons
声速剖面采集时刻为2023年4月3日19点10分09秒,声速采集结果如图11所示。
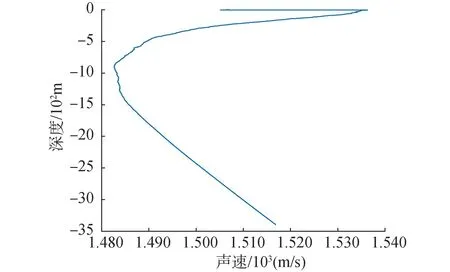
图11 声速剖面Fig.11 Sound velocity profile
基准间交互周期为20 s,J1、J2、J4的转发时延分别为0、0.8、2.4 s。信标时钟源是型号 SA.45 s的铷钟,135 h累积漂移小于1.5×10-4s。所以可以认为试验期间钟差不变。假设各信标以发射时刻作为本地时钟的0时刻,各信标钟差Φ分别为0、0.8、2.4 s。试验共采集了206个周期的互测信号,各信标以自身发射时刻为参照,记录其余信标信号到达时刻。如所图12~14所示,可知时延测量值波动幅度均低于1×10-4s。该误差主要来源为声速变化。该幅度是钟差测量精度上限,也是离散化计算时,设置分辨力的主要依据。分辨力过高会影响计算速度,过低则会降低同步精度。本次试验数据钟差分辨力设置为1×10-5。

图12 J1测量时刻值Fig.12 J1 measurement time values

图13 J2测量时刻值Fig.13 J2 measurement time values

图14 J4测量时刻值Fig.14 J4 measurement time values
3.2 试验结果
试验共采集206个周期的数据,但实际一个周期数据已经足够解算出信标钟差。如图15、16所示,随着冗余消息的增加,峰宽逐渐减小,同步精度逐渐提高,向分辨度1×10-5s靠拢。J2测量准确度高于8×10-4s,J4测量准确度高于7×10-5s。
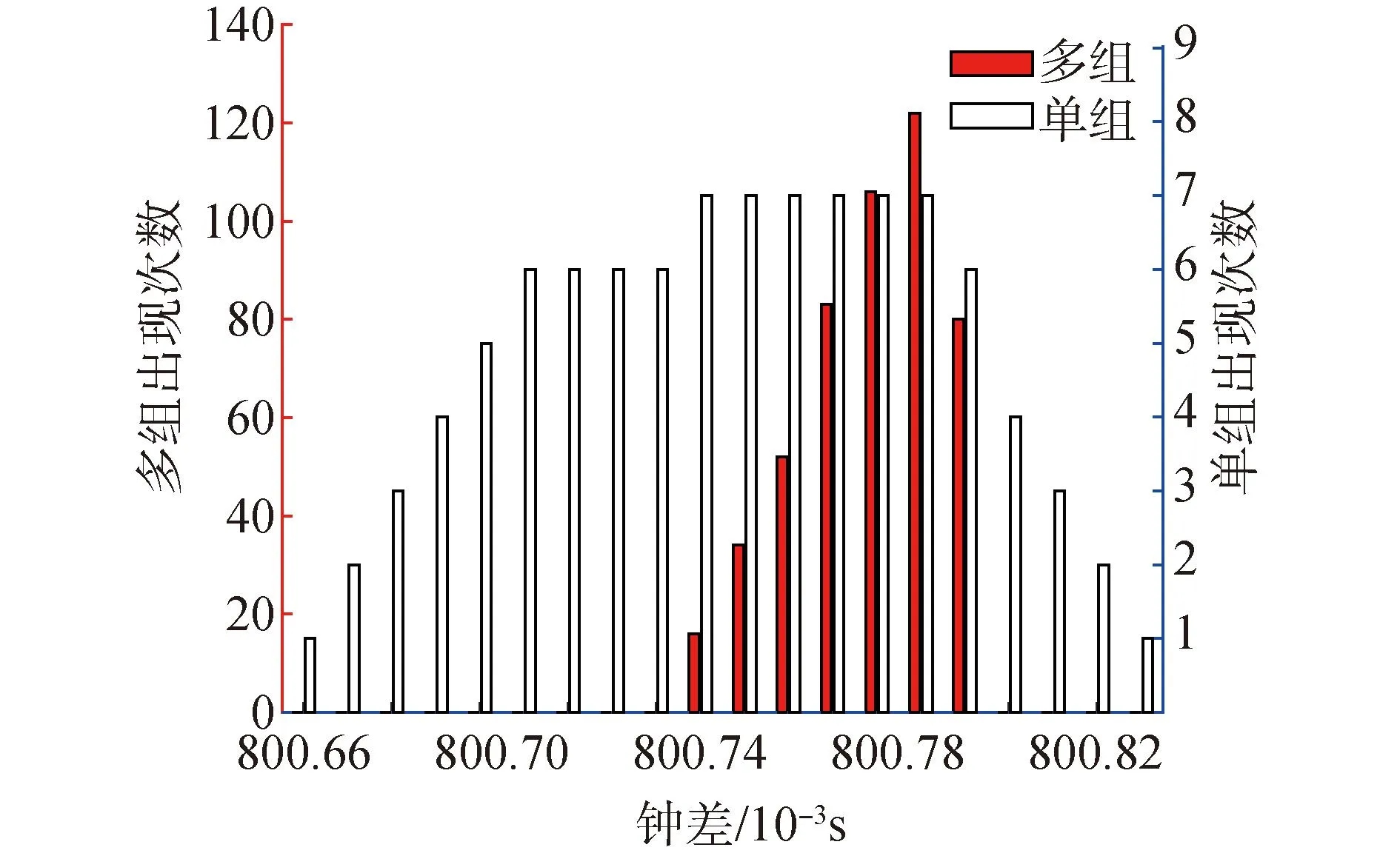
图15 J2钟差估计Fig.15 J2 clock deviation estimation
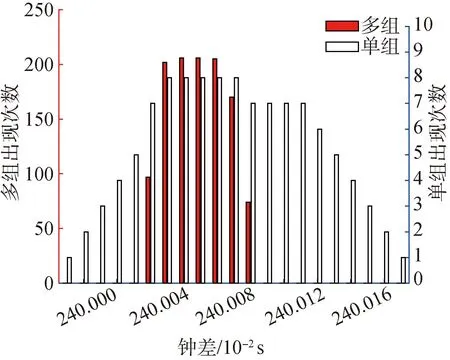
图16 J4钟差估计Fig.16 J4 clock offset estimation
不同交互次数下,概率图法和DE方法估计结果对比如图17、18所示,2个方法的钟差估计准确度一致,但概率图法每个周期均可得到一次同步结果。相比之下,DE方法需要2个周期完成一次交互才可获得一次同步结果,同步效率较低。
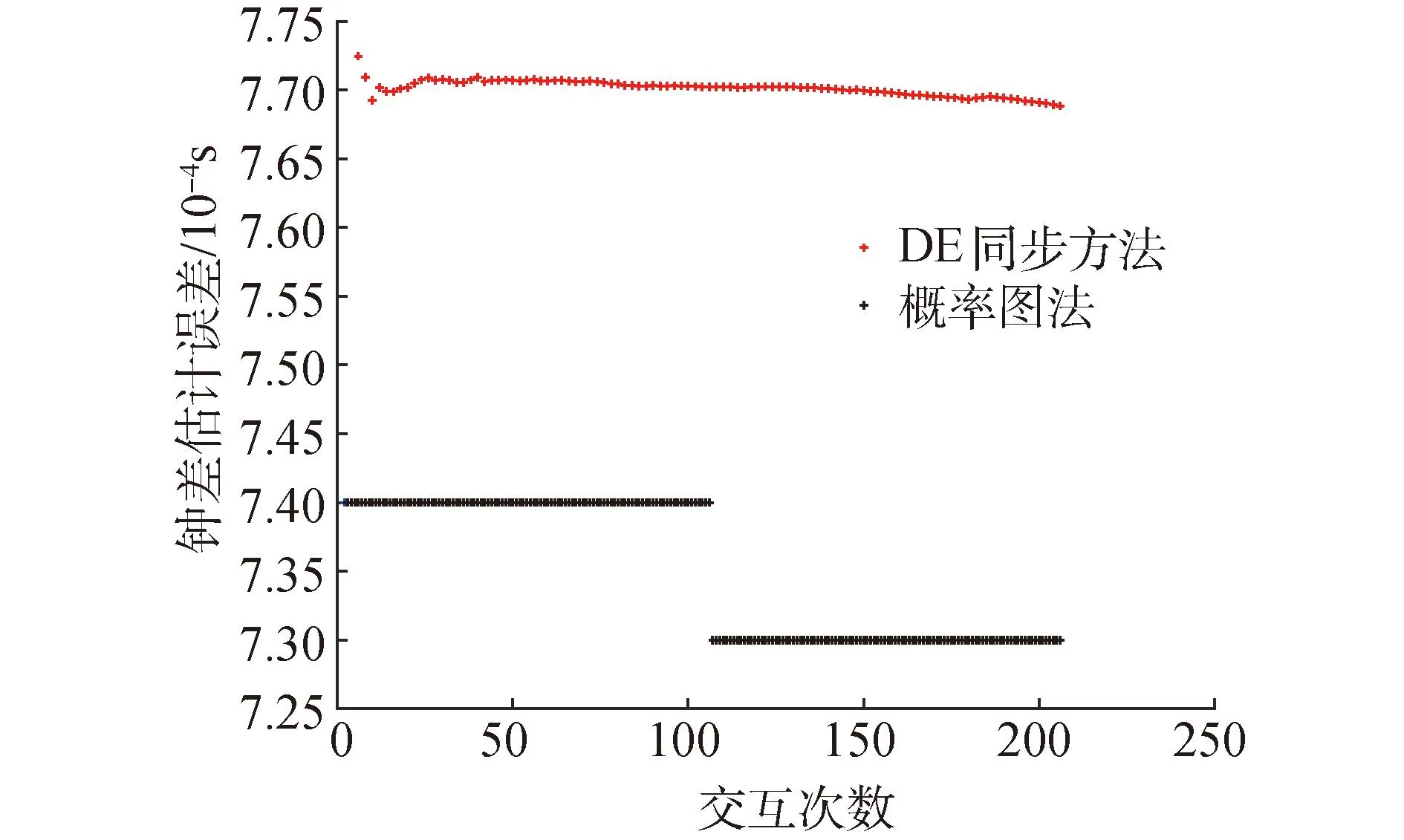
图17 J2钟差估计误差对比Fig.17 J2 clock deviation estimation error comparison

图18 J4钟差估计误差对比Fig.18 Comparison of J4 clock deviation estimation errors
4 结论
1)与现有方法相比具备计算复杂度低,同步效率高的优点,其同步精度主要受到时刻测量精度与分辨力的限制。
2)仿真结果表明,时间同步精度随分变率提升而增高,当分辨力超过时刻测量精度后,曲线趋于平稳。受限于计算能力,分辨力一般取值高于时刻测量精度即可。
3)实验结果也证明在到达时刻测量精度不高于1×10-4s,分辨力为1×10-5s时,时间同步估计精度到达1×10-5量级。估计精度随着样本增多而逐渐收敛。此外该方法在融合位置、声速与其余信标钟差信息后,仅需一个周期便可完成整个传感器网络的时间基准统一。

