基于低轨全覆盖卫星星座的反向缝建链策略

万 威，曾 媛，任欣悦，欧阳尚荣

（上海航天测控通信研究所，上海 201109）

0 引言

低轨卫星网络是指轨道高度一般为300～1 500 km 且具备星间链路的卫星网络通信系统。低轨卫星网络具有覆盖面积大、可靠性高等特点。利用卫星网络的覆盖面广，不受地域、自然灾害影响等特性，有效地解决地面网络所面临的问题［1-2］。在卫星网络中，其拓扑设计以及网络拓扑中的反向缝链路设计均是极其重要的一环。

卫星星座需根据任务进行设计［3-4］。低轨卫星网络一般承担对地观测和通信任务，要求对地常态化覆盖、通信时延小［5-6］。但低轨卫星星座运动速度快，过顶时间短，导致链路切换频繁，网络维护开销大［7-8］。卫星轨道设计方法通常有几何解析法、仿真比较法、基于优化算法的设计方法［9-11］。几何解析法计算简单、易于实现，但设计效率低；仿真比较法设计灵活，可兼容多类性能指标，但较难找到系统最优解；基于优化算法的方法可完成不对称星座的设计，但计算量大，解空间与模型参数之间可解释性差，易导致损失函数难以收敛。

低轨极轨卫星星座反向缝问题不可忽视，反向缝处卫星相对角速度较大，可见时间短，存在建链困难的问题。反向缝指1 个轨道面的上行轨（往北极）相邻轨道面的下行轨（往南极）间形成的1 条相邻、运行方向相反的环带［12］。针对该问题，现已有较多解决方案。例如，不建链准则［13］、最近卫星准则［14］和最长可视时间准则［15］实现简单，但易导致卫星网络平均跳数大［16］、链路变化频繁，增加网络维护开销，减少建链数目。交叉建链准则（Cross-Link Building Criteria，SCLBS）［17］相较上述算法已有所改进，但仍未能平衡链路数目及链路持续时间。

本文针对卫星网络的拓扑问题，构建全覆盖的通信卫星星座，并在该星座下，提出了一种高连通性的反向缝链路构建策略。主要工作如下：

1）针对低轨卫星星座构建问题，提出一种基于轨道覆盖带（Satellite Orbit Coverage，SOC）［18］的低轨卫星星座设计方法，该方法综合考虑地面终端通信仰角和SOC 方法在轨间存在相位差情况下，边缘区域切换频繁问题，实现全球持续性覆盖。

2）针对反向缝问题，提出一种反向缝轨道间通信链路构建策略，即邻轨k最近邻星策略，该方法通过折中链路数目与链路长度，获得网络稳定性与网络连通性的平衡。

1 面向全覆盖的卫星星座设计

本文基于SOC 设计方法，提出一种低轨圆形极轨卫星星座的设计方法。该方法满足低轨卫星网络对地面持续性全覆盖［19］的通信需求，同时，考虑地面终端设备通信仰角与边缘地区的切换问题，降低网络开销。

SOC 方法使用多条极轨圆轨道（单轨道中卫星均匀分布）构建星座，以达到全球覆盖，如图1 所示。该方法在保证赤道区域连续覆盖的情况下，随着轨道间距由赤道向两极缩小，覆盖高纬地区，达到全球覆盖［20］。

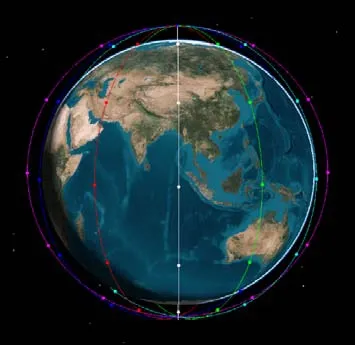
图1 星座Fig.1 Constellation diagram

SOC 方法在轨间相位差情况下，存在覆盖边缘区域切换频繁的问题。SOC 切换如图2 所示。由图2 可知，中阴影部分表示卫星覆盖边缘，移动节点NM表示地面站，随着卫星沿着箭头方向运动，NM的接入卫星按照S1、S3、S2的顺序频繁切换，增加网络开销。

图2 SOC 切换Fig.2 Switching scheme of SOC

针对上述问题，本文提出的设计方法通过收紧SOC 方法中的轨间间距条件，实现地面全覆盖，减少边缘区域卫星切换频率，如图3 所示。在本文所提出设计方法下，移动节点NM会按照S4、S3切换，频率明显低于SOC 方法。收紧轨间间距条件后，轨间是否存在相位差对覆盖性能与边缘区域的切换次数均不会产生影响。

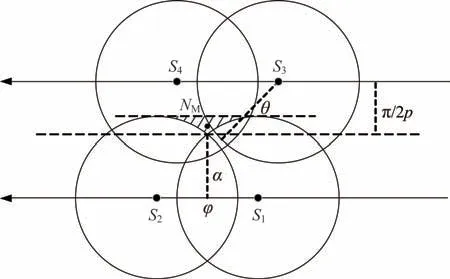
图3 设计的轨道覆盖带Fig.3 Designed SOC

以下为本文方法覆盖性推导，如图3 所示。将每颗卫星Si的覆盖区域固定为其对应的半地心角θ，假设星座有p根轨道，每根轨道由n颗卫星构成。可得轨道覆盖带对应半地心角α表达式如下：

通过式（1）得到α的最小值为。轨内卫星均匀分布，因此可得到轨内星星间距地心角φ表达式如下：

从图4 中摘取出S1、M、P，加入地心点O，如图5所示，由于面POM⊥面MOS1通过三线角定理可得：

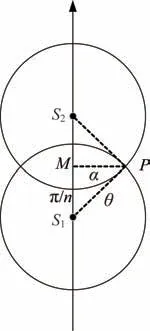
图4 单轨道覆盖带Fig.4 SOC of a single orbit

图5 地心角Fig.5 Geocentric angle

将地面最小通信仰角ε与轨道高度H纳入考虑［21］。卫星覆盖区域剖面如图6 中所示。

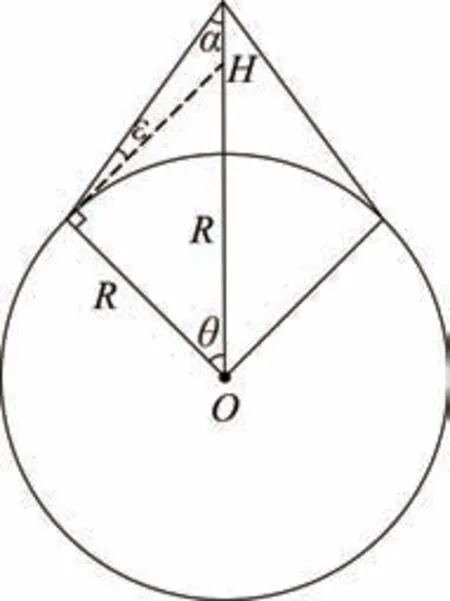
图6 卫星覆盖区域剖面Fig.6 Profile of the satellite coverage area

由图6 可知，圆形为地球地表，虚线为地表该点的切线。通过加粗边框三角形，构建正弦定理可得表达式如下：

根据式（5）可得，H、ε与θ3 个参数之间的关系，结合式（4），可得表达式如下：

忽略地球引力不均、月球潮汐作用等因素，通过上式，即确定H和ε后，可确定卫星星座轨道数p、每根轨道卫星数n。

由于轨道高度在1 000～1 500 km 之间存在范艾伦带，会影响飞行器使用寿命，所以卫星星座的轨道高度选择需避开范艾伦带，选择1 000 km 以下。但如果轨道高度过低，飞行器也会受到大气的摩擦，所以轨道高度不能选择过低。系统最小地面通信仰角ε≥10°，地球半径则取均值6 371 km，轨道高度选取 709 km。则通过式（5）可得θ=17.601°。当单轨卫星数n=12 时，可得p≥9.66。当n=18 时，可得p≥6.18。通过式（6）即可得出全球连续覆盖星座参数，见表1。

表1 卫星星座设计参数Tab.1 Parameters of the satellite constellation design

根据上述数据，反向缝设计策略基于10×18的卫星星座进行仿真。

2 邻轨k 最近邻星建链策略设计

在卫星网络运行中，由于地球对卫星具有遮挡效应，卫星仅可与视距范围内的卫星建链。卫星在同轨内的链路，其天线指向保持不变，轨内链路永远处于建链的状态。而两极处异轨卫星间相对运动速度过大，导致天线难以追踪，卫星在两极处会关闭异轨间通信链路，导致周期性的通断。周期性的通断及卫星本身的运动使星间网络具有高动态特性。针对这一特性，目前已提出3 种解决方法，虚拟拓扑策略、覆盖域策略和虚拟节点策略。其中最主要的解决方式为虚拟拓扑策略，即将卫星星座按照运行周期划分为多个时间片，在时间片内，认为卫星与卫星之间的链接关系固定不变［22］。由于时间片更换时，拓扑中链路状态发生更迭，需重新收敛卫星网络的路由信息。因此减少反向缝处链路切换次数，可减少卫星网络路由的重收敛次数［23］。

反向缝两侧的卫星由于反向运动，2 根轨道间卫星的相对速度为卫星相对地球运动速度的2 倍左右，相对角速度过大，天线转动角速度也相应增大，跟踪变得更加困难。但如不在反向缝两侧建链，会导致整体网络端到端时延增大。由于卫星运动具有周期性，而在反向缝两侧的链路运动相反，所以与卫星建链的卫星也具有周期性，且如果设计合适的建链策略，可使在反向缝处的链路具有较小的传输代价，同时降低链路切换次数。所以本文设计了一种邻轨k最近邻星建链策略，以解决反向缝建链问题。

2.1 算法描述

设定地球半径为R，星座轨道数为p，每根轨道卫星数为n，且轨道中卫星呈均匀分布，轨道高度为H的卫星星座，在该星座中构建坐标系。忽略潮汐作用、大气阻力等影响卫星运动的因素，卫星周期为T。构建反向缝两侧的轨道上的卫星运动方程［24］，第1 根轨道的表达式如下：

最后一根轨道的表达式如下：

式中：αi、αj为轨道中每颗卫星的轨内相位；ω为卫星运动角速度，rad/s；t为时刻，s；N为整数的集合；∆σ为相邻轨道相位差；i、j为轨道上的卫星序号；x、y、z为卫星在J2000 坐标系下的坐标。

对于建链双方卫星，单星需满足建链的条件1为：星与星之间建链需满足卫星当前的位置均处于极地域外，即需满足如下表达式：

式中：re为极地域纬度，（°）（N/S）。

需满足建链的条件2 为：星与星之间的建链满足可见性要求。对于上述星座，卫星可见范围δ的表达式如下：

可确定邻轨k最近邻星策略中k的取值范围如下：

通过上述2 个方程组，得到任意时刻卫星的坐标。通过三维坐标系下的欧式距离计算即可求得任意时刻任意卫星对之间的距离

k的取值：求得卫星i与邻轨卫星距离的集合Di后，判别2 个建链条件，选取最小距离对应卫星j；选取j行进方向上的后k颗卫星，将到达j位置的卫星，(j+k)进行建链。

对于静态网络，用1 个穿过最少链路数的截面将网络划分为2 个对等的子网，此时截面中链路的传输速率之和称为此网络的半分带宽。本文提出采用反向缝动态最大带宽B来描述在一个时间片周期内，反向缝处链路的传输速率和的上限，其计算公式如下：

式中：Tslot为时间片长度，s；(i，j+k)为建链卫星对；D(i，j+k)为该卫星对之间的距离，m；C(D(i，j+k))为 该链路的信道容量，bps。

在空间自由衰落的前提下，信道容量的表达式如下：

式中：W为信道带宽，单位；Pt发送功率，W；Gt、Gr分别为发送天线和接收天线的增益，dB；λ为信号的波长，m；N0为噪声功率谱密度，W/Hz。

式（12）与式（13）组合后，可得出反向缝动态最大带宽B与链路长度与链路持续时长的关系。k值越大，链路持续时长越长，链路数目越少，D(i，j+k)均值越大，C越小，B越小；k值越小，链路持续时长越短，链路数目越多，D(i，j+k)均值越小，C越大，B越大。

本文所提邻轨k最近邻星策略，可通过调整k的取值，折中链路长度、链路数目与链路持续时长，获得不同的建链方式。对不同的建链方式进行仿真，即可得到该建链方式下的动态半分带宽；对动态半分带宽及链路链接情况展开评判，可获取在当前拓扑下最优建链方式。不同大小的星座拓扑，所获得的最佳k值不同。

2.2 算法实现

在本文所提星座模型下，本文假设每颗星最多与4 颗相邻星建链，其中2 根同轨链路不随卫星的运动而发生状态变化，2 根异轨链路随着卫星进入极地域即断开。本文所设计的邻轨k最近邻星建链策略（Thekth Nearest Satellite In Adjacent Orbits，kth NSAO）见表2。

表2 邻轨k 最近邻星建链策略Tab.2 kth NSAO

经计算，可得k仅有3 个取值即0，1，2。当k取0时，为最短建链策略；取1 时，折中链路长度与链路数目，保证链路的长度不至于太长而导致链路衰减过大。在之后的讨论中，k将取值为1。k取1 时的链路切换时刻如图7 所示。其中，箭头表示反向缝处2 根不同的轨道与轨道上的卫星的运行方向。卫星标号为S(a，b)，S表示卫星，a表示卫星的轨道标识，b表示在轨道中卫星的序号。横向虚线表示当前链路的链接状况；实线表示即将构建的链路，竖向虚线表示极地域划分的纬度线。

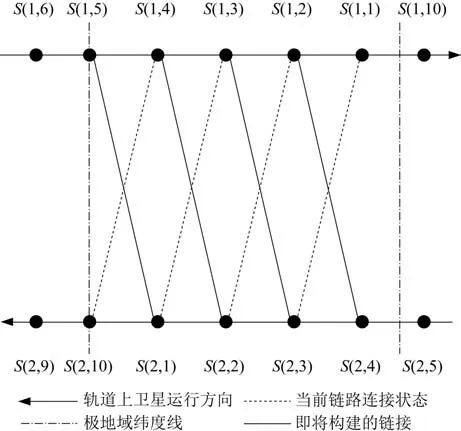
图7 反向缝链路Fig.7 Cross-seam links

例如S(1，3)，当前与链路的目的星为S(2，1)，如果此刻链路发生切换，首先判断卫星S(1，3)是否需构建反向缝的星间链路，判断本星位置是否处于极地域。

由图7 可知，星S(1，3)不在极地域中，继续寻找目的星。与S(1，3)相邻的距离最小的星为S(2，2)，根据 可见性，可得可建链星为S(2，10)、S(2，1)、S(2，2)、S(2，3)、S(2，5)根据相邻轨道的运动方向与卫星标号可得，目的星为S(2，3)、S(2，4)。再判断星S(2，2)、S(2，3)、S(2，4)均不处于截止域，可得k取值0，1，2，最后通过k不同取值时的网络传输能力与网络连通性进行判断，S(1，3)、S(2，3)构建反向缝处的星间链路。这条星间链路可维持到时间片更换，或2 颗星中2 颗或任意1 颗进入极地域。

邻轨k最近邻星建链策略算法伪代码见表3。

3 仿真分析

本文所提出的邻轨最近邻星策略的验证选用前文所述的全球连续覆盖低轨星座作为验证平台，极地域纬度re的选取为80。为验证本文设计的算法，选取最近邻星策略与交叉建链策略展开分析对比。

仿真环境选取Matlab、STK。从STK 中进行星座设计并导出星座数据，将星座位置信息导入Matlab 中进行链路计算与仿真。STK 中仿真总时长 为24 h，2023 年7 月30 日4 时 至2023 年8 月30 日4 时，仿真步长设置为6 s。

本文所提出的星座设计方案通过缩小SOC 设计方法的轨间间距，减少用户切换次数，降低网络切换开销。地面最小通信仰角为10°，轨道高度为709 km，轨道卫星数n=18 时，SOC 设计方案需满足轨道数p≥6，本文所提方案需满足p≥7。不考虑卫星网络中的流量情况与用户情况，当用户位于赤道时，轨间间距最大，用户发生切换的可能性最大（各星覆盖区域的重叠部分最小），选取赤道处建立地面站，对2 种设计方案的切换性能进行仿真。由于卫星轨道轨道高度较低，如仿真时间设置为1 h，卫星对地速度远大于地球自转速度，不考虑地球自转时，切换性能如图8（a）、图8（c）所示。由图可知，本文所提出的方案中，地面站建链方式明显少于SOC 设计方法，地面站选取位置在两轨道中间，即卫星覆盖边缘区域时，SOC 切换次数为18 次，本文所提出方法切换的次数为9 次，减少50%。考虑地球自转影响，即地面站相对于卫星轨道呈运动状态时，仿真结果如图8（b）、图8（d）所示。由于地面站用户所处边缘区域时间减短，SOC 方法下切换次数明显减少，为10 次，本文所提方案中的切换次数为9次，相较于经典SOC 方法减少10%。

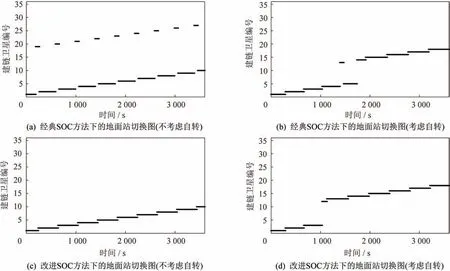
图8 采用不同SOC 设计方案的地面站建链情况Fig.8 Link construction performance of the ground station under different SOC design schemes

在STK 中，对本文设计的卫星星座进行切换次数全覆盖性能仿真。结果如图9 和图10 所示。由图9 可知卫星星座的整体覆盖性能，其中锥形区域代表单颗卫星的覆盖范围，星座的瞬时覆盖率达到100%。

图9 卫星星座覆盖性能三维视Fig.9 Three-dimensional view of the satellite constellation coverage

图10 卫星星座覆盖性Fig.10 Coverage performance of the satellite constellation

图10（a）为星座的瞬时覆盖率的仿真结果图，图10（b）为星座累计覆盖率结果图，由以上两图可知，在仿真持续时间内，卫星星座的瞬时、累计覆盖率均为100%，且保持恒定。综上所述，本文设计的低轨卫星星座可达到全球连续覆盖。

在本文所构建的星座中，采用邻轨k最近邻星建链策略。受可见性约束限制，该卫星星座中k的取值范围为[0，2]，k∈N。k=0 时，即最短建链策略。在卫星的1 个运行周期内，由于反向缝两侧的链路相向而行，异轨间链路切换较为频繁。采取最短建链策略时，建链次数接近于邻轨卫星数目；采取邻轨k最近邻星建链策略时，链路切换次数随着k值的增加而减少，链路持续时长也随着k值的增加而增加。在以下仿真中k取值为1，如图11 所示，在各建链策略下，反向缝处单颗卫星在一个运行周期内的建链情况。在各建链策略下的链路平均持续时长与链路在一个运动周期内的切换次数见表4。

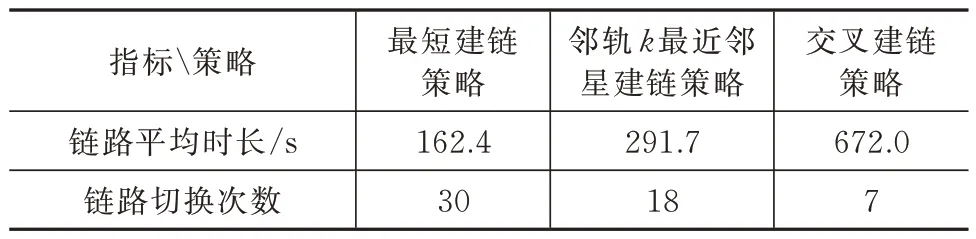
表4 各策略下建链情况Tab.4 Link performance under different strategies

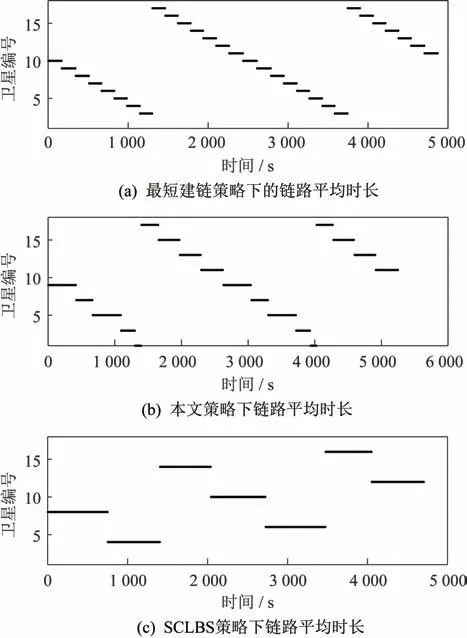
图11 单颗卫星建链情况Fig.11 Link performance of a single satellite under different strategies

各策略下建链情况见表4。结合图11 和表4 可知，邻轨k最近邻星建链策略相较于最短建链策略，会切换次数减少，链路持续时长增加，且链路切换次数随着k值的增大而持续减少，当切换次数受可见性约束而缩小到一固定值时，为最长时间建链策略。

比较星座在不同建链策略选取下网络的健壮性。在1 个时间片内，认为网络处于静止状态，所以在该时间片内，对反向缝两侧轨道上所有卫星建链，可将卫星网络拓扑视为静态，并将此时的静态网络抽象为1 个无向图G(V，E)，其中V代表无向图中的顶点的集合，即卫星节点；E代表无向图中边的集合，即链路［25］。在图中，自然连通度-λ通过量化冗余路径的加权值，表征图的冗余路径丰富度，可简单理解为拓扑结构的连通性。其计算公式如下：

式中：Node为图中所有节点的数目；λi为图的邻接矩阵的第i个特征根描述在该建链规则下整体网络的健壮性或连通性。

在邻轨k最近邻星建链策略下，反向缝处链路数目随着k值的增大而减小。对于-λ反应网络的冗余路径丰富度，整个网络链路数目越多，-λ值越大，即当k减小时，链路数目增多，-λ值越大。不同的网络拓扑结构，-λ的值也不同，k取值较小时，链路持续时间较短，网络中链路变化越频繁，-λ值波动越大，即网络稳定性越差，-λ变化越大。

综上可知，网络稳定性是k值的隐函数，且与k呈正相关。网络传输性能即反向缝处动态半分带宽B，同为k值的隐函数，且与k呈负相关。可得到下式：

通过上式对网络稳定性与动态半分带宽进行仿真分析，确定网络稳定性与动态半分带宽的变化趋势并进行平衡，确定k最优取值，平衡网络稳定性与网络传输性能，即折衷考虑链路数目与链路持续时长。

4 种反向缝建链策略的网络连通性仿真结果如图12 所示，邻轨k最近邻星网络连通性如图13 所示。由图12 可知，本文所提方案明显优于不建链准则。最短建链准则链路数目大于本文所提策略，其网络连通性瞬时极大值较高，同时其链路切换频繁，网络稳定性远低于本文所提策略。交叉建链策略链路数目相较于k取1 时更少，但链路持续时间，即网络稳定性会得到一定的提升。由图13 可知，k的不同取值在网络稳定性上相差无几，但连通性随着k值增大而减低。

图12 各策略下的网络连通性Fig.12 Network connectivity under different strategies

图13 邻轨k 最近邻星网络连通性Fig.13 Network connectivity of different k in the kth NSAO

3 种反向缝建链策略下的网络动态半分带宽仿真结果如图14 所示。由图14 可知，邻轨k最近邻星在网络中的动态半分带宽部分优于最短建链准则，但整体性能不如最短建链准则稳定。

各策略下半分带宽均值见表5。由表5 可知，邻轨k最近邻星均值略低于最短建链准则，但相较于交叉建链策略，有显著优势。

表5 各策略下半分带宽均值Tab.5 Values of the dynamic bisection bandwidth obtained by different strategies

通过仿真可得，本文所设计的星座拓扑中，邻轨k最近邻星建链策略在k取值为1 时，为最优k取值，相较于交叉建链策略，以损失23.58%的反向缝处平均半分带宽为代价，使网络拓扑稳定性提升79.62%；以损失56.59%的拓扑稳定性为代价，使反向缝处平均半分带宽提升137.45%，更好地平衡反向缝处网络稳定性与网络传输性能之间的矛盾。

在超大型星座中，不同k值的选取，使网络性能存在差异，对于不同星座，最佳k值的选取也会不同，但在一定的范围内接近于最优解。

4 结束语

针对低轨卫星星座设计问题，本文提出一种基于SOC 设计方法的改进方法，在保证持续性覆盖性能的前提下，通过收紧轨间间距约束条件，减少边缘区域的切换次数，降低网络维护开销。并设计了一种低轨卫星星座反向缝链路构建策略——邻轨k最近邻星策略，通过可见性约束、极地域约束提出网络动态半分带宽和网络流量上限，约束网络整体性能，以获取最佳k取值。在本文所设计的卫星星座中进行建链仿真，结果表明，应用本文所提出策略，在星座设计时，通过收紧轨间间距，获取更少的切换次数；在反向缝建链时，通过对链路数目与链路持续时间的折衷，获得最优或次优的k值，使网络的稳定性得到提升。同时更易获得网络稳定性、连通性及传输性能的最优解。

未来将基于该卫星星座与建链策略，进一步研究卫星网络的移动性管理策略、路由算法等。