Studying the Equilibrium Points of the Modified Circular Restricted Threebody Problem: The Case of Sun–Haumea System

I.Nurul Huda, B.Dermawan, M.B.Saputra, R.Sadikin, and T.Hidayat

1 Research Center for Computing, National Research and Innovation Agency, Bogor, Indonesia; ibnu.nurul.huda@brin.go.id

2 Department of Astronomy and Bosscha Observatory, FMIPA, Institut Teknologi Bandung, Bandung, Indonesia

Abstract We intend to study a modified version of the planar Circular Restricted Three-Body Problem (CRTBP) by incorporating several perturbing parameters.We consider the bigger primary as an oblate spheroid and emitting radiation while the small primary has an elongated body.We also consider the perturbation from a disk-like structure encompassing this three-body system.First,we develop a mathematical model of this modified CRTBP.We have found there exist five equilibrium points in this modified CRTBP model,where three of them are collinear and the other two are non-collinear.Second,we apply our modified CRTBP model to the Sun–Haumea system by considering several values of each perturbing parameter.Through our numerical investigation,we have discovered that the incorporation of perturbing parameters has resulted in a shift in the equilibrium point positions of the Sun–Haumea system compared to their positions in the classical CRTBP.The stability of equilibrium points is investigated.We have shown that the collinear equilibrium points are unstable and the stability of non-collinear equilibrium points depends on the mass parameter μ of the system.Unlike the classical case, non-collinear equilibrium points have both a maximum and minimum limit of μ for achieving stability.We remark that the stability range of μ in non-collinear equilibrium points depends on the perturbing parameters.In the context of the Sun–Haumea system, we have found that the non-collinear equilibrium points are stable.

Key words: celestial mechanics – Kuiper Belt: general – planets and satellites: dynamical evolution and stability

1.Introduction

Celestial mechanics plays an important role in understanding the dynamics of solar system bodies (see, e.g., Murray &Dermott 1999; Souchay & Dvorak 2010; Lei 2021; Pan &Hou 2022).One of the problems in celestial mechanics is the Circular Restricted Three-Body Problem (CRTBP).The study of CRTBP has the aim to investigate the movement of an infinitesimal object under the gravitational influence of two primaries that have a circular orbit around their center of mass.CRTBP has several applications, such as for deep space exploration and satellite navigation.The classical version of CRTBP assumes the primaries are point masses and it only considers the gravitational interaction between them.There are five equilibrium points in the case of planar.Three of them are collinear (L1, L2, and L3) and the other two are non-collinear(L4and L5) (Murray & Dermott 1999).In order to make the CRTBP model more realistic, the classical version has been modified by considering several additional parameters.

A stellar object, including the Sun, emits radiation.This radiation exerts pressure on objects in its path.There have been numerous studies that have considered radiation pressure force as another additional force in the restricted three-body problem (see, e.g., Haque & Ishwar 1995; Ishwar & Elipe 2001; Kushvah et al.2007; Kushvah 2008a; Das et al.2009;Yousuf&Kishor 2019;Patel et al.2023).For instance,the first study on this topic was done by Radzievskii(1950).Chernikov(1970) extended the study by considering the relativistic Poynting–Robertson effect.Simmons et al.(1985) examined the effect of radiation pressure force in all ranges of value.More recently, Idrisi (2017) and Idrisi & Ullah (2018)considered the effect of planetary albedo on CRTBP as a consequence of solar radiation pressure force.

Since the stars and planets are not perfectly spherical,another aspect that has been considered in the CRTBP is the oblateness of the primaries.Early studies about the impact of an oblate primary on the dynamics of restricted three-body problem were published by Danby (1965), Sharma & Subba Rao (1978, 1986).More recently, the effect of oblateness on the dynamics of CRTBP has been studied in detail by several authors (see, e.g., Markellos et al.1996; Douskos &Markellos 2006; Safiya Beevi & Sharma 2012; Abouelmagd et al.2013; Zotos 2015; Yousuf et al.2022).Moreover, some authors have considered the effect of both oblateness and radiation force in their calculation.For instance, Singh &Ishwar (1999) studied the linear stability of triangular equilibrium points when both primaries are oblate and emitting radiation.This study was extended by Singh (2009) for the nonlinear stability of L4.AbdulRaheem & Singh (2006)investigated the dynamics of CRTBP when both of the primaries are oblate and emit radiation, together with perturbations in the Coriolis and centrifugal force.Other authors, such as Nurul Huda et al.(2015), Dermawan et al.(2015) and Mia et al.(2023), considered the effect of oblateness and radiation force in the Elliptic Restricted Three-Body Problem.

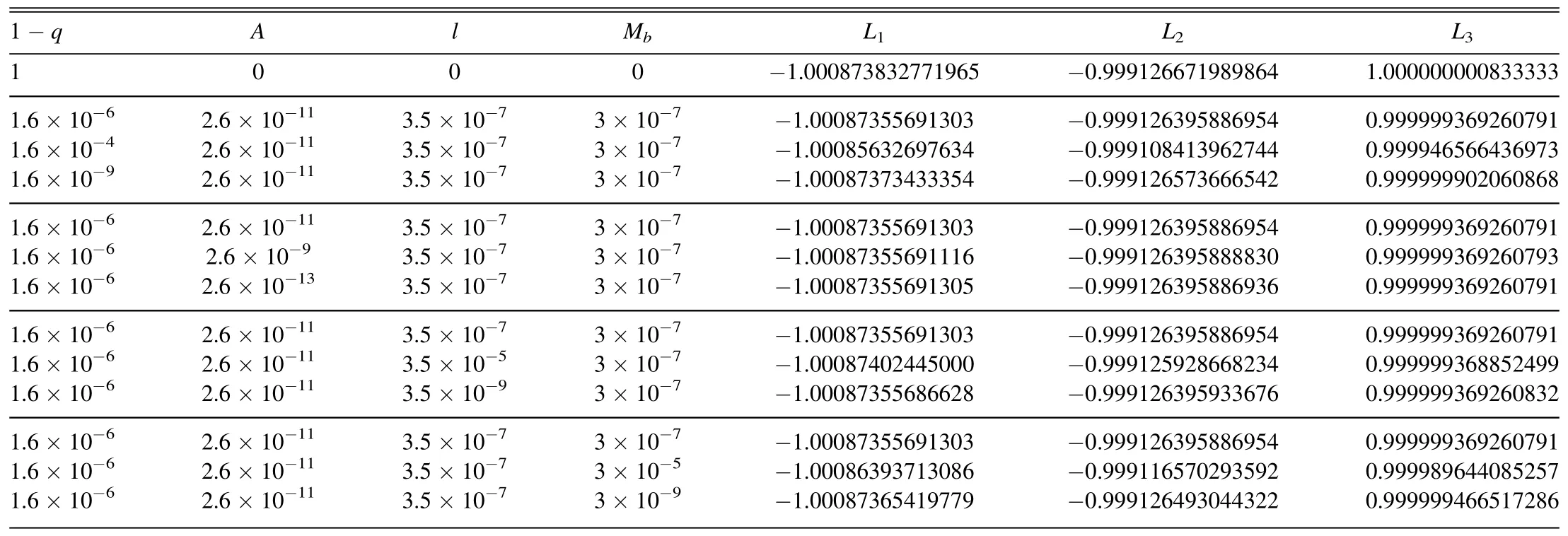
Table 1 The Abscissa Position of Collinear Equilibrium Points (L1, L2, and L3) in Sun–Haumea System with μ=2×10-9 and T=0.11

Our solar system contains several types of celestial bodies.Among them are elongated objects like a few asteroids,comets,and dwarf planets.These celestial bodies can be approximately described as finite straight segments.Previous studies of CRTBP have been enriched by assuming one or both primaries have an elongated body.At first, Riaguas et al.(1999) and Riaguas et al.(2001) analyzed the dynamics of a two-body problem by considering one of the primaries as a finite straight segment.These works were extended by, e.g., Jain & Sinha(2014), Kaur et al.(2020), and Kumar et al.(2019), into the restricted three body-problem assuming both or one of the primaries have elongated shapes.In more recent studies,Verma et al.(2023a) examined the perturbed restricted three-body problem,where the smaller primary has an elongated shape and the larger primary is oblate and emits radiation.Verma et al.(2023b) considered the effect of a finite straight segment and oblateness to study the dynamics of the restricted 2+2 body problem.

Meanwhile,the effect of a disk-like structure as a perturbing force near a three-body system has been well studied by several authors (see, e.g.,Jiang & Yeh 2004; Kushvah 2008b;Kushvah et al.2012; Kishor & Kushvah 2013; Mahato et al.2022a).Jiang & Yeh (2004) considered CRTBP by analyzing the influence of a disk-like structure near the three-body system.Yousuf&Kishor(2019)analyzed the effect of a disklike structure, oblateness, and albedo on the CRTBP.Mahato et al.(2022a) extended the study of classical CRTBP by considering a disk-like structure and an elongated body.Mahato et al.(2022b) investigated the stability of equilibrium points within a framework of the perturbed restricted 2+2 body problem, taking into account the influence of a disk-like structure.

This study aims to obtain the collinear and non-collinear equilibrium points and investigate their stability under a framework of modified CRTBP incorporating the effect of radiation pressure,oblateness,finite straight segment,and disklike structure.We intend to extend the work of Yousuf &Kishor (2019) by assuming the small primary to be a finite straight segment rather than being oblate.It is also an extension of Mahato et al.(2022a) since we consider the effect of oblateness and radiation from the bigger primary.

Here we apply our modified CRTBP model to the Sun–Haumea system by assuming the Sun is a bigger primary with an oblate shape and emitting radiation and Haumea is a smaller primary which has an elongated body.We also consider the Kuiper Belt as a disk-like structure surrounding the Sun–Haumea system.Haumea was chosen as our case study because of its unique characteristics, which have captured the attention of scientists since its discovery in 2003.The surface of Haumea is dominantly covered by water ice (Barkume et al.2006;Pinilla-Alonso et al.2009; Noviello et al.2022).There is also evidence that organic material exists on Haumea’s surface(Lacerda et al.2008; Gourgeot et al.2016).Recently, it was discovered that Haumea has a ring and two satellites named Namaka and Hi’iaka (Ortiz et al.2017).Moreover, previous studies have proposed Haumea as a destination for space missions in the coming decades (see, e.g., Grundy et al.2009;Sanchez et al.2014).

Besides the Sun–Haumea system, this modified CRTBP model can be applied to other cases.For instance, many planetary systems outside of our solar system have beendiscovered, and some systems have been found to have dust particle disks or asteroid belts,which are believed to be similar to the Kuiper Belt or main belt in our solar system (see, e.g.,Greaves et al.1998; Matrà et al.2019).Meanwhile, previous studies explained the presence of extrasolar asteroids or dwarf planets near the host star (see, e.g., Jura 2003; Dufour et al.2010).Moreover, some space explorations have been devoted to exploring small solar system bodies near the main belt or Kuiper Belt region.It is known that several solar system bodies have an irregular shape.Therefore,it is reasonable to study the combined effects of perturbations from a disk, an elongated body, and an oblate radiating body on the motion of an infinitesimal mass in the CRTBP.

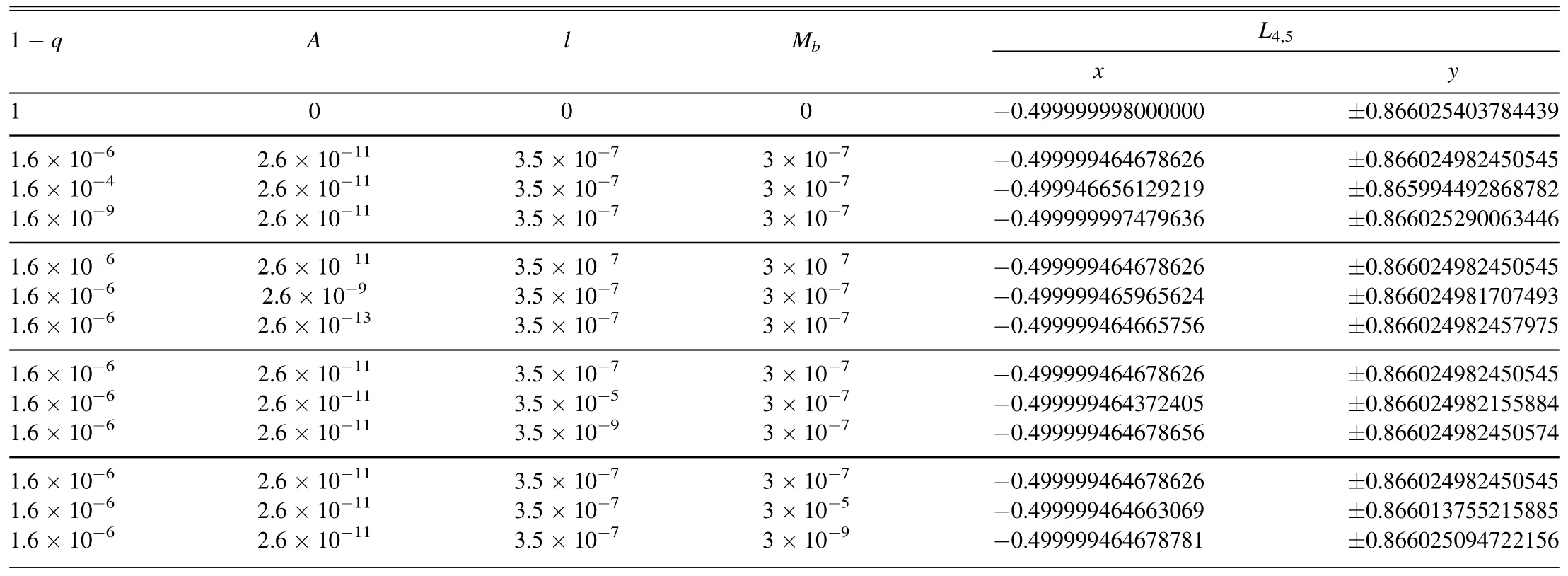
Table 2 Positions of Non-collinear Equilibrium Points (L4 and L5) in Sun–Haumea System with μ=2×10-9 and T=0.11

The structure of this paper is as follows.In the next section,we present a mathematical formulation of the dynamical model.The position and stability of equilibrium points are elucidated in Section 3.Section 4 describes the implementation of the dynamical model in the Sun–Haumea system.Finally, the conclusion is provided in Section 5.Here, MATLAB’s Symbolic Toolbox is used to conduct certain algebraic calculations and find numerical solutions.

2.Mathematical Formulation of the Dynamical System

In this work, we consider a system where an infinitesimal mass moves under the influence of a bigger primary with mass m1and a small primary with mass m2.The primaries of this system have circular orbits around their center of mass.We treat the bigger primary as a source of radiation with an oblate spheroid shape, while the small primary has an elongated shape.The unit of time is normalized to make the Gaussian constant of gravitation equal to one.The mass parameter is represented by μ=m2/(m1+m2) where m1=1-μ and m2=μ.In the case of a restricted three-body problem, it is more convenient to introduce the system in the rotational coordinate Oxy.The primaries are located on the x-axis with the distance between primaries chosen as the unit of length.The coordinates of the bigger primary, small primary, and the third body are (μ, 0), (μ-1, 0), and (x, y), respectively.The oblateness factor of the bigger primary can be represented by A=(AE2-AP2)/5R2where A ≪1, AE and AP represent the equatorial and polar radii, respectively, and R is the effective radius when assuming the primary to be a spherical object.Meanwhile, the radiation force Fpacts opposite to the gravitational force and diminishes with respect to distance.The total force acting on the bigger primary can be written as Fg-Fp=qFg, hence q=1-(Fp/Fg).Here q is called the mass reduction factor where 0<1-q ≪1.The small primary is assumed to be a finite straight segment with length 2l.The effect of a disk-like structure surrounding the system is also considered in this study.Following Miyamoto&Nagai(1975),the planar version of unitless potential disk-like structure is given byV(x,y) =Mbr2+T2, where Mbis the total mass of disk-like structure,r2=x2+y2is the radial distance of the infinitesimal mass,and T=a+b is the total of flatness and core parameters.Let the distance of primaries to the center of mass be s1and s2.Considering the previous works such as Kushvah (2008b), Yousuf & Kishor (2019), and Mahato et al.(2022a), the motion of the primaries is given by

3.Equilibrium Points

3.1.Position of Equilibrium Points

In the following, we solve Equations (5) and (6) to find the position of equilibrium points.

The collinear points are located in a line with the primaries,thus we have y=0.Equation (5) becomes

In order to find the solution, we divide the region into three parts, i.e., (-∞, μ-1-l), (μ-1-l, μ), and (μ, ∞).Here L1, L2, and L3are the solution located in (-∞, μ-1-l),(μ-1-l, μ), and (μ, ∞), respectively.Hence we have

These three equations have been solved numerically to find each collinear equilibrium point.Only the real solution is considered for the position of equilibrium points.

Meanwhile, there are two non-collinear equilibrium points,i.e., L4and L5.The additional condition of these equilibrium points is y ≠0.Equations (5) and (6) can be rewritten in the form

The calculations of ∊1and ∊2are done by substituting Equation (13) into Equation (12) and Equation (11) and solving these equations.By approximating with series and neglecting higher order terms of ∊1, ∊2, l2, and A, we have:

3.2.Linear Stability

Let us assume a small displacement in an equilibrium point by defining

where “o” corresponds to the equilibrium points.The equation of motion from this small displacement is expressed as follows:

where

Here Ωomeans the pseudo-potential is evaluated at equilibrium points.Hence it is constant.Equation(18)has general solutions

where αiand βiare constants while λiis the root of the characteristic equation.Substituting Equation (22) into Equation (18) produces

4.The Case of Sun–Haumea System

In this work,we model the Sun–Haumea system through the framework of the restricted three-body problem with the Sun as the bigger primary and Haumea as the small primary.Here we also consider the Kuiper Belt in this system.We assume Haumea has a circular orbit and orbits in the same plane as the Kuiper Belt.The mass of the small primary is a combination of Haumea’s mass and the mass of Haumea’s satellites: Namaka and Hi’iaka.The Sun has a mass around 1.989×1030kg.Haumea has a length of ∼2300 km for its largest axis and a mass of 4×1021kg (Ragozzine & Brown 2009).Meanwhile,Namaka and Hi’iaka have masses of 1.79×1018kg and 17.9×1018kg,respectively(Ortiz et al.2017).Hence we have μ=2×10-9and l=3.5×10-7.Following Yousuf & Kishor(2019),here we assume that the Sun has A=2.6×10-11while the Kuiper Belt has T=0.11 and Mb=3×10-7.According to Sharma (1987), the photogravitational parameter q can be expressed in the CGS unit system as q=1-(5.6×10-5/aρ)where a and ρ are the radius and density of a moving body,respectively.Assuming a spacecraft has a=700 cm and ρ=0.05 gr cm-3, 1-q=1.6×10-6.

Characteristic Roots of Collinear EquilibriumT a Pbolien t3 s in Sun–Haumea System with μ=2×10-9

Figure 1.Plot of μ vs.characteristic roots(λ1,2,3,4)for L1,L2,and L3,with l=3.5×10-7,Mb=3×10-7,A=2.6×10-11,and 1-q=1.6×10-6.The real and imaginary parts of characteristic roots are marked by solid and dotted lines, respectively.Here we used T=0.11.

We calculated the position of the collinear equilibrium points of the Sun–Haumea system.By substituting the property of the system into Equation (8) and solving it numerically, we found L1, L2, and L3.Table 1 shows the position of collinear equilibrium points.Here we vary the value of each perturbation parameter to examine the impact on the equilibrium point position.In the case of L1, the position gets closer to the primaries if A and 1-q increase.Decreasing A and increasing 1-q make L2be closer to the bigger primary.The position of L3is nearer with respect to primaries if the bigger primary emits stronger radiation pressure.According to Table 1, the position of collinear equilibrium points depends on the value of Mband l.Increasing Mband decreasing l make the location of L1become nearer to the smaller primary.The increment of Mband l affects the position of L2to become closer to the bigger primary.L3gets closer to the primaries if we increase the value of Mb.

The positions of non-collinear equilibrium points are calculated from Equation (16).Table 2 shows the positions of non-collinear equilibrium points with respect to the chosen value of several parameters.When there are no perturbing factors, the triangular points have the same coordinates as in the classical case.The inclusion of perturbation parameters has resulted in a shift in the location of non-collinear equilibrium points.The increment of A makes the position of these equilibrium points closer to the small primary.In contrast,if we reduce q or increase Mb,the positions of equilibrium points are shifted toward the bigger primary.The positions are closer to the bigger primary in line with the increase of l.

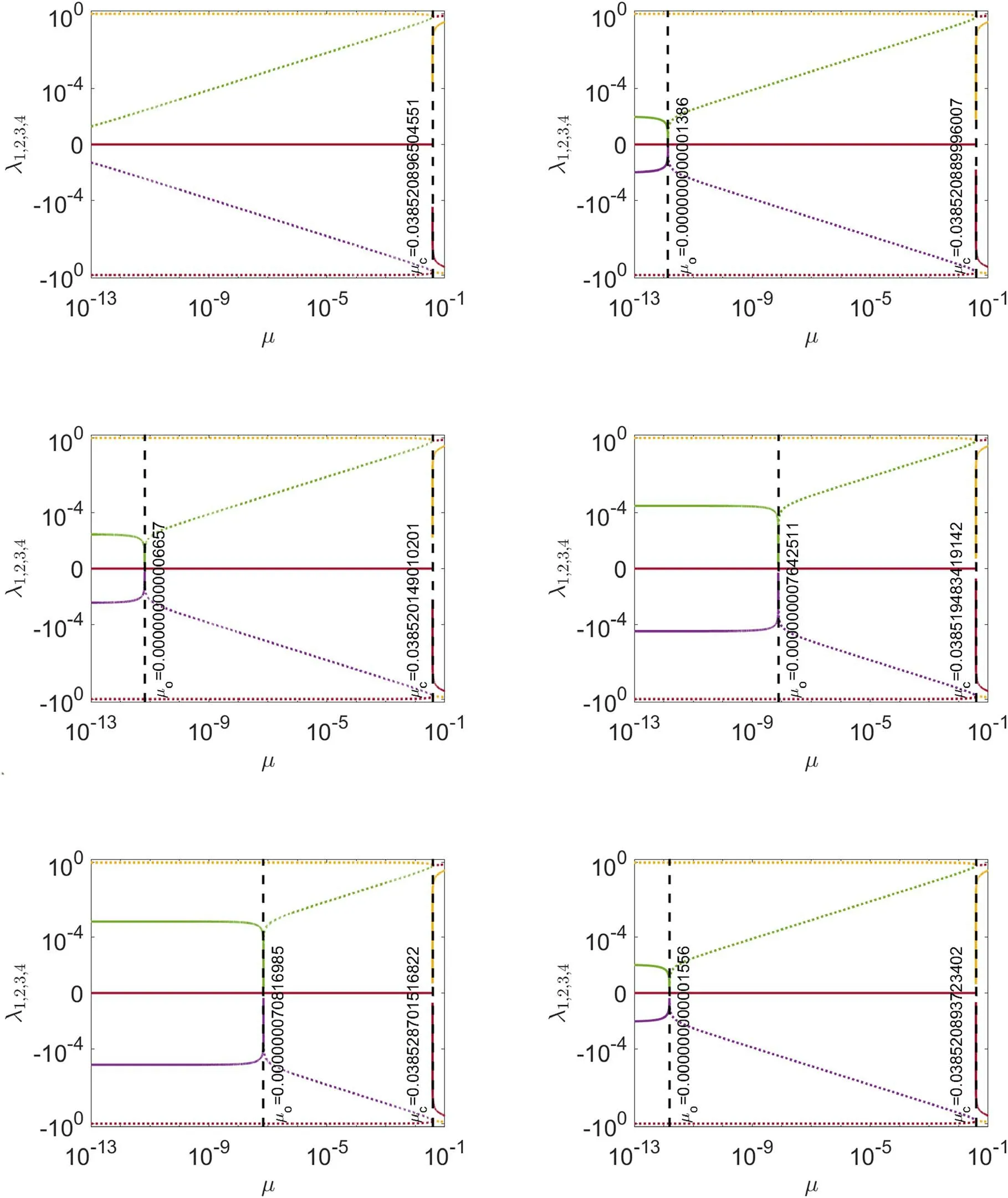
Figure 2.Plot of μ vs.characteristic roots(λ1,2,3,4)in L4 with different parameter configurations.The real and imaginary parts of characteristic roots are marked by solid and dashed lines respectively.Here we use T=0.11.The details of the parameters that are used in each subfigure are as follows.(a) A=0, 1-q=0, l=0,Mb=0.(b) A=2.6×10-11, 1-q=1.6×10-6, l=3.5×10-7, Mb=3×10-7.(c) A=2.6×10-6, 1-q=1.6×10-6, l=3.5×10-7, Mb=3×10-7.(d)A=2.6×10-11, 1-q=1.6×10-4, l=3.5×10-7, Mb=3×10-7.(e) A=2.6×10-11, 1-q=1.6×10-6, l=3.5×10-7, Mb=3×10-4.(f)A=2.6×10-11, 1-q=1.6×10-6, l=3.5×10-4, Mb=3×10-7.

We now analyze the linear stability of each equilibrium point in the Sun–Haumea system.Collinear equilibrium points lie in the abscissa.Hence we have Ωoxy= 0.In order to study the stability, we divide the abscissa into three regions, i.e., L1(-∞, μ-1-l), L2(μ-1-l, μ), and L3(μ, ∞), and calculate the sign of b and b2-4c numerically for each region.First, we estimate the stability by considering the perturbation parameters in the Sun–Haumea system.As shown in Figure 1,there exist pure real and pure imaginary characteristic roots for μ between 0 and 0.5.Hence,all collinear equilibrium points of the Sun–Haumea system are unstable.Furthermore, we conducted the calculation by varying the value of perturbation parameters.Table 3 displays the result of the calculation.All regions have b<0 and b2-4c>0 which mean it produces two real pairs and two pure imaginary pairs.This shows that even if we change the value of perturbation parameters, the collinear equilibrium points remain unstable.

Next, we investigate the stability of non-collinear equilibrium points in the Sun–Haumea system.We discuss only L4since the dynamics of L5is nearly similar.In the classical case,non-collinear equilibrium points are stable under the condition 27μ(1-μ)<1.Hence we can deduce μ<μc, where the critical mass μc=0.038520896504551.This critical mass can be calculated by finding the solution of b2-4c=0.In this modified version of CRTBP,we numerically calculate the roots by solving Equation (24).By considering the perturbing parameters, it shows that the stability of non-collinear equilibrium points has a maximum limit (μc) and minimum limit(μo)of mass parameters,an aspect which is different from the classical case.For the Sun–Haumea system, we found μc=0.0385208896007 and μo=1.386×10-12.Since the Sun–Haumea system has μ=2×10-9, we conclude that the Sun–Haumea system has stable non-collinear equilibrium points.Figure 2 displays a comparison of stability for several cases by changing the perturbing parameters of the Sun–Haumea system.It shows that the range of stability depends on the parameters A,q,l,and Mb.The characteristic roots have the form of pure imaginary if μo<μ<μc.The considered perturbation parameters alter the range of stability in μ.The increment of A or reduction of q reduces the size of the stability area.The stability region is shifted toward bigger μ if Mband l increase.

5.Conclusion

We have investigated the dynamics of an infinitesimal mass under the gravitational influence of two primaries.Our study assumes that the smaller primary is an elongated body, while the larger primary is oblate and also emits radiation.In addition,we have taken into account the presence of a disk that surrounds the three-body system.We have found that there are five equilibrium points in this modified CRTBP such that three of them are collinear and the other two are non-collinear.Our numerical exploration of the Sun–Haumea system has revealed that the inclusion of perturbing parameters has caused a displacement in the position of the Sun–Haumea system’s equilibrium points with respect to their positions in the classical CRTBP.We noticed that the magnitude of the perturbing parameters(q,A,l,and Mb)can affect the positions of the five equilibrium points.This analysis shows that the non-collinear equilibrium points of the Sun–Haumea system are stable,while all collinear equilibrium points are unstable.Moreover, we have ascertained that the collinear equilibrium points remain unstable for several possible ranges of perturbing parameters.In contrast, the non-collinear equilibrium points are conditionally stable with respect to μ.When taking into account the perturbing parameters, we have found that there are upper and lower limits of μ for achieving stability of non-collinear equilibrium points.The stability region for μ depends on the perturbing parameters.

Acknowledgments

This work is funded partially by BRIN’s research grant Rumah Program AIBDTK 2023.We thank the anonymous reviewer for the insightful comments and suggestions on the manuscript.